下载文档原格式
静电场电势零点选择的讨论吴树刚（河池学院 物理与电子工程系 物本05A 班 广西 宜州 546300）【摘 要】在人们日常生活、生产和学习中，静电场电势零点是可以任意选取的，通常是选取地球或无穷远处为零势点，这仅仅适用于分布在有限区域的特殊带电体所激发的电场。
本文将结合实例由特殊到一般进一步探讨分布在无限区域的电荷所激发的电场零势点的选取，以及探讨如何选取零势点更有利于解决问题的具体方法。
【关键词】零点电势；静电场电势；有限空间；无限空间1 引言研究静电场可以从力和能两方面入手，电场强度是从力的方面描述静电场的物理量，为了从能方面描述静电场，要引入电势这个物理量。
静电场是保守场，其任意两点之间的电势差是确定的，可是场内任意一点的电势却取决于电势零点的选择。
选择适当的零点电势可以使问题简化。
在平常我们一般选大地或者无穷远点为电势参考点，但是像零点电势选择的任意性；为什么选大地、无穷远点为电势零点？还有分布在无限大区域的带电体系能不能选无穷远点为电势零点？为什么常选0U U ∞==地等问题，许多学者已经做过详细的理论分析，但是结合具体实例来论证的相对比较少，本文将运用理论结合实例的手段来对零点电势的选择做进一步的分析与讨论。
2 零点电势选取的任意性在物理学中，电势就像高度和重力势能这些物理量一样，都是相对量。
对于它们的大小，我们必须要选择一个参考点以后，它们才有确切的物理意义。
也就是说，单独孤立的的讨论某点电势的高低是没有意义的。
对于选择不同的参考点，某点的电势可有不同的数值。
显然参考点的变化是要影响电势的分布的，但是电场却没有改变。
由此，我们可知：不同的电势可以描述同一个电场的，从而得出零点电势的选取是具有任意性的。
我们在物理学上是这样定义电势U 的p pU d =⋅⎰E l当将参考点0p 定在0p '时，上式变为 （0p 是参考点，p 是场点）p p pp U d d ''=⋅+⋅⎰⎰E l E l0p pd U '=⋅+⎰E l由上式说明，参考点变化时，各点电势只改变一个常量0p p U d '=⋅⎰E l但是这并不影响电场强度0()U U U =-=-+E ∇∇的分布，如考虑一维则为0()d U U dUdr dr+=-=-E 由于静电场电势参考点的选择具有任意性，那么能够选择适当的零势点，便能使电势具有一个简单简洁的表达式。
分析静电场中零势点的选择作者：周明来源：《科学导报·学术》2019年第05期摘要：在静电场中，电势是一参考量，所以只有在零电势点确定后，才可谈空间中的电势，零电势选择得当可使问题简化，选择不当，则会使电势的表达形式比较繁琐甚至出现无确定的值。
本文将从几种典型电场的零电势位置的确定，说明选择零电势点的一般原则和方法。
关键词：静电场；零势点；选择一、电势零点选择的任意性和受限性1.电势零点选择的任意性电场中某点的电势是相对零电势点而言的，静电场力把单位正电荷从场点p处移到参考点处所作的功是。
例如带电量为正的点电荷电场，若选无穷远处为电势零点，则电场中任意点的电势为 = 其中是场点到点电荷的距离，若零电势点选在距点电荷rA处，则 = （）显然，电势零点选择位置不同，该点的电势值不同，但它们都有确定的物理意义，且零势点的选取不会影响电势的变化规律。
因此，对于点电荷，它的零电势点无论选在何处，电场，其性质没有变，所以我们可以这样说，对于点电荷电场，电势零点的选择具有任意性。
2.电势零点选择的受限性电势零点的选择虽然带有一定的任意性，但也受一定条件限制，这个条件是：电势零点一旦选定，电场中各个点电势必须具有确定的值，否则就毫无意义，即积分必须是收敛的，所以说电势零点的选择要依具体问题具体分析。
由一定带电体系所决定的电场，其场强是场点的矢量函数，它的形式一般为其中A是与场源电荷分布情况，场源电荷电量大小及选取单位有关的比例系数，r指场点至带电体或至带电体系中心的距离，m为整数，电场中某一点的电势可写为：= =从上式可以看出，电势参考点的选取由m决定，下面分三种情况讨论电势。
（1）当m>1时，零电势参考点的选取此时，电场中p点的电势可写为 = = =A ，对（1）式，当取无穷远处为电势零点时，当取电场中某一点为电势零点时，当取带电体本身的电势为零时，例如点电荷的电场，电偶极子的电场，电四极子的电场 =三式都是电荷分布在有限的区域内电场强度的表达式，且其中的m均大于1，只是在选无穷远的电势为零时，它的数学表达式最为简单，便于我们处理问题。
关于静电场势能零点的选取的讨论电势是电学里的一个很重要的概念，我读了这篇文章后，对电势的选取有了进一步的认识。
由文献中已知点电荷的场不能选取点电荷所在处为电势零点，无限大均匀带电平面和无限长均匀带电直线或圆柱的场不能选取无穷远点为电势零点。
可见，对电势零点的选择的限制都出现在某些理想化的情形。
理想模型是实际情形的近似和抽象，它不仅带来许多方便，而且也是建立物理规律和理论必不可少的手段。
上述特殊情形出现的困难和矛盾（如电势不确定，电势为无穷大），既不能否定普遍的结论（如静电场是势场），也不能否定理想模型的重要作用，关键在于弄清楚理想模型的适用条件，才能正确理解电势零点选取的限制。
对零势点的选取分为以下几个方面：1、在计算点电荷产生的电势时,不能选取场源电荷本身所在的位置为电势零点,通常选取无限远处为电势零点 ,得出电场中距离场源电荷为r的一点的电势：q/4r2、有限大的带电体通常可选择无限远处为电势零点电场中其他各点的电势值即可确定。
3无限大带电体,比如“无限长”的导线,或者“无限大”的平面,“无限长”的圆柱面等带电体,这些理想化的物理模型,其上面的电荷分布延伸到无限远处,在计算这些带电体在周围空间产生的电势时,就不能选取无限远处为电势零点,而只能选取其周围一点有限远处为电势零点,利用电势的相对性和电由高斯定理可知,“无限长”均匀带电直线周围任一点电场强度的大小: E =λ/2π 0 r因此电势零点选取的原则是使计算的电势值有意义,并且使电势的表达式尽可能简洁。
电势是一个相对量，它的大小、正负与电势零点的选取密切相关。
我们在选取零势能点的时候要具体问题，具体分析。
只有这样，才能得出正确而又简洁的答案。
0902010325 水利水电学院黄蕴晗。
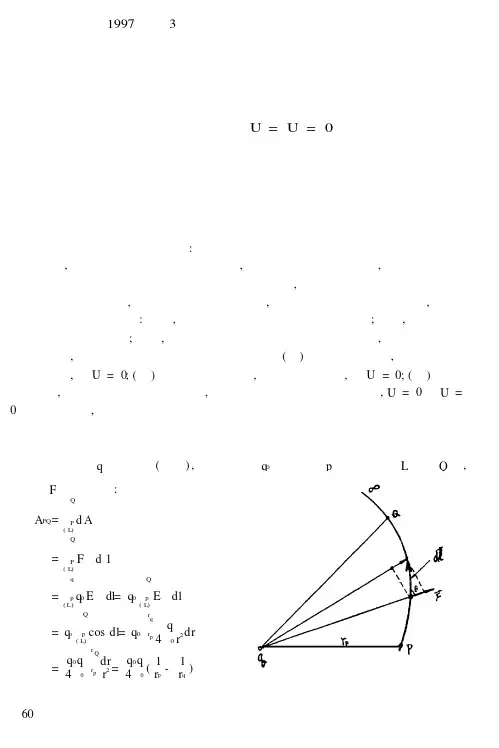
农垦师专学报 1997年第3期静电场电势参考点的选择与讨论——如何理解U ∞=U 地=0谷秋竹 杜学山静电场中某一点的电势定义为:单位正电荷从该点经任意路径到参考点电场力所做的功。
可见,电势是一个具有相对性的物理量,要考查电场中某点的电势,必须首先选择一个零电势作为参考点。
而参考点的选择原则上是任意的,但在实际选取时又不完全是任意的。
若参考点选择不当,不仅会造成计算上的繁琐,还容易出现错误。
就简略而言,参考点的选择必须满足三个条件:第一,必须使电场中各点的电势具有确定值;第二,在同一问题中只能选择一个参考点;第三,电势的数学表达式应该尽可能简单。
因此,在讨论电场中某点的电势时,对于电势零点的一般选择方法有三种。
(一)对于有限带电体,选择无限远为电势参考点,即U ∞=0;(二)对于接地带电体系,选择地为参考点,即U 地=0;(三)对于无限带电体,选择任意点为参考点。
那么,为什么选择无限远与地为参考点,U ∞=0与U 地=0又是否等价呢,下面分别举例说明。
一、为什么选择无限远为参考点 设在点电荷q 的电场中(图一),把试探电荷q 0从任一点p 沿任意路径L 移到Q 点,电场力F 所做的功为: A PQ =∫QP (L )d A =∫Q P (L )Fd l =∫q p (L)q 0E →dl →=q 0∫Q p (L )E →dl → =q o ∫Q p (L )cos θdl=q 0∫r q r p q 4πε0r 2dr =q 0q πε∫r Q r dr 2=q 0q πε(1-1q) 图一640p r 40r p r 0故P 、Q 两点间的电势差为U P Q =A q 0=∫Q p E →dl →=q 4πε0(1r p -1r q)(1)因电势参考点的选择是任意的,若选择无限远处一点为参考点时,则有U P =U p ∞=∫∞p E →dl→(2)或U P =U p ∞=q 4πε0r p(3)由此可见,在选择无限远为参考点后,静电场中的电势表达式仅有一项。
电磁场与电磁波研究报告静电场零电位的选择胡鸿09211054刘思聪09211039陶坤纬09211044目录静电场电位零点选择的任意性 (1)为什么选择无穷远处为电位零点 (2)为什么选择U地=0，它和U∞=0是否相容 (4)零点不同的电位如何相加 (5)收获和体会 (7)参考文献 (9)一、静电场电位零点选择的任意性从物理的角度说明电势零点选择的任意性从物理的角度上看, 静电场与重力场相似, 都是保守力场, 可以引入势能的概念, 电势能是相互作用的电荷系统所具有的, 孤立地谈论某一点的电势能或电势的高低和正负是没有意义的。
为了确定电场中各点的电势, 就要选定参考点, 也就是势能零点, 它的选择必须满足一个条件, 那就是零点选定后, 空间各点的电势必须有确定的值。
选择不同的参考零点, 静电场中各点的电势值虽然有所不同, 但两点之间的电势差仍然相同, 描述的仍然是同一个静电场。
这就是电势零点的选择在原则上任意的物理原因。
从数学的角度说明电势零点选择的任意性从数学的角度上看, 电势从单位正电荷在静电场中各点所蕴含的能量来描述场, 电势是描述静电场的标量位置函数。
根据定义:当参考点从p01到p02时, 各点的电势只改变一个常量不影响场强分布:。
反映在几何图像上(如图1 ( U - r) ) , 零点选择不同, 只是横坐标的位置不同, 横坐标改变, 不会影响曲线上各点的斜率。
静电场电势零点选择的限制性以上讨论了电势零点选择从原则上是任意的, 但是我们在解题时又遇到了一些问题, 发现电势零点的选择在一些特殊情况下又会受到一定条件的限制。
这个条件正如前面提及的: 电势零点一旦选定以后, 就必须使电场中各点的电势都具有确定的值, 这样才有物理意义,否则毫无意义。
即积分:必须是收敛的。
有了这个条件, 电势零点的选择便依具体问题而定了。
二、为什么选择无穷远处为电位零点1.电量和分布范围均有限，当所研究的观测点到带电体几何中心的距离远大于带电体的几何尺寸时．带电体的形状及电荷分布对观测点的影响可以忽略，此时带电体可以按几何点来处理2.离带电体系足够远(在物理上)而可称为无穷远点的广大空间,是具有零场强和恒定电位的位置3.普遍适用又方便自然在几乎一切实际静电场问题中，尽管带电体系的电量、分布各异，但电量和分布范围均有限。
因此，根据问题要求的精度，在离带电体系足够远(在物理上)而可称为无穷远点的广大空间,是具有零场强和恒定电位的位置，尽管实际静电场问题的具体条件不同，但都存在着具有上述性质的“无穷远点”，这是共同的普遍特点。
点电荷为物理学中的一种数学模型。
从物理学上讲，任何带电体都具有一定的大小和形状。
当所研究的观测点到带电体几何中心的距离远大于带电体的几何尺寸时．带电体的形状及电荷分布对观测点的影响可以忽略，此时带电体可以按几何点来处理。
这就是点电荷。
当观测点到带电体几何中心的距离与带电体的几何尺寸相当时，带电体就不能再看作是点电荷了，只能作为有限带电体来处理。
当带电体的尺寸远大于观测点到带电体几何中心的尺寸时。
带电体将被视为无限大。
可见，点电荷，有限带电体。
无限带电体都是处理物理问题的数学模型。
而无限远处则是带电体对该处电场的影响达到了可以忽略程度的地方.把它选作参考点，取U。
=0，即普遍适用又方便自然，这就是通常选取U。
=0的原因。
而在某些理想化的问题讨论中，上述问题却出现了例外，例如考虑一个均匀带正电的无穷大平面。
用高斯定理不难求出它周围的场强分布，为了讨论它周围的电位分布，可在带电平面外附近任取一点。
如果把单位正电荷从该点沿着平面的法线方向，即沿电场方向移到无穷远时，电场对单位正电荷做功为无穷大，因此该点电位(绝对值)为无穷大，但如果把单位正电荷沿平面的切线方向，即沿垂直于电场的方向移到无穷远时，电场对单位正电荷做功为零，于是该点的电位为零。
静电场是保守场，空间各点电位的数值是相对的，其大小与零电位的选择有关。
零电位选在什么位置有利于问题的处理? 目前教科书普遍认为，零电位是人为规定的，位置选的不同．其结果仅为公式的繁简不同。
现以点电荷为例来证明，对于不同的带电体模型，在零电位选取时，将因其数字模型与物理实际的差异。
带来处理问题上的局限性，从而导致空间零电位的选取存在限制条件。
三、为什么选择U地=0，它和U∞=0是否相容？接地的目的：在实际应用中常常把电势零点选在地球上,凡接地的导体电势皆为零。
下面讨论接地的目的：首先将地球看作是一个导体球, 表面不带电, 不存在电场。
根据以前学过的知识静电屏蔽，首先, 如果空腔导体（不接地）内没有带电体, 则不论导体壳是否带电或是否处于外电场中, 壳表面保护了它所包围的区域, 使之不受壳外表面电荷或外电场的影响, 起了对内屏蔽的作用。
其次, 把它放在接地的金属壳内, 由于地球是导体, 接地使壳外表面的感应电荷流入地下, 使带电体不影响外界, 可把消除了内部带电体对外的影响, 接地导体壳起了对外屏蔽的作用。
因此接地的目的是使壳内外场强互不影响, 而且使壳内外电位互不影响, 维持稳定的平衡分布。
前提条件：不论流入地球的电荷是多少, 地球的电位稳定, 可取为零, 且U地=0和U∞=0相容。
在静电场问题的讨论中，在有限的范围内和一般实际问题的处理中均可选择U地≈U∞=0，条件一是导体球离地的距离必须远大于导体的尺寸。
这样, 导体可认为是孤立的, 对导体而言, 大地和无穷远可视为等价；二是题中所涉及的电量, 都远大于109-库仑/米2这个数量级, 从而, 由于地球本身所带的电荷对题目解答的影响可以忽略不计。
四、零点不同的电位如何相加1.如果同时存在几个静电场，且各个静电场的零电势点选取不同，此时总的静电场的电势如何表达？总电势的零点如何选择？均匀外场E0中放入一个点电荷q 如图所示。
以点电荷所在处为坐标原点，建立球坐标系。
均匀电场的电势为U1，选原点为均匀电场的零电势点，则；点电荷的电势为U2，若选无穷远为点电荷的零电势点，则；合电场的电势，通常表示为2.不同的电势可以这样相加吗？其含义是什么？对于任何静电场，无论电势零点如何，电势表达式中，与变量有关的函数项的形式总是一定的。
零点不同，电势不同，但它们只相差一个常数。
零点的变化，只会影响电势表达式中的常数项。
点电荷电场电势随空间变化的规律取决于，均匀电场的电势取决于，合电场的电势变化规律取决于，电势零点的变化，只改变U0的取值。
上式中U1, U2的相加是合理的。
对此也可以用电势曲线来说明，如图所示。
以电势U 为纵坐标，r 为横坐标。
点电荷电场的电势曲线如图中曲线①所示，均匀电场的电势曲线如图中曲线②（此时取θ=0 ）。
电势零点的变化，只会使电势曲线沿纵轴上下平移，并不改变电势曲线的形状，也不会改变曲线①、②的相对位置。
叠加以后，曲线①和曲线②合成的曲线③，曲线③表示了合电势的变化规律。
电势零点的变化对曲线③而言也只能使其沿纵轴上下平移，而不会改变其形状。
这也说明不同电势零点的电势相加的合理性。
【收获和体会】胡鸿课堂的学习我知道电位的值与电势零点的选择有关，但没有从根源上了解有关零电位选取的知识。
通过这次研讨课题，我们结合了以前学过的知识，并查阅了很多文献资料，明白电位零点的选择具有一定的任意性,如果选取适当,可以使问题简化。
但零点的选取往往又受到一些限制,如果选取不当,会导致空间的电位值失去意义。
这次研讨对我们对课本内容的彻底消化有很大的帮助。
陶坤纬在这次研究学习后，让我们对于零电势的选择有了更深的认识，在不同零电位下的电势虽然不同，但是电势差相同，实际上，这就是电势与电场强度的微积分关系，零电位的不同，仅仅是电势常数项的不同而已。
所以在调节不同零电势点下的不同电势和，仅需统一一个电势常数项，也就是统一了零点势点，从而解决问题。
刘思聪在这次电磁研讨中，我们在选题方面可能看起来做得有些简单，也不是什么高深的前沿问题。
但是，静电场方面是电磁场的基础，而且零电势点的选择是和我们的电磁课程关系密切的。
在许多练习题目中，都有关于零电势点的选择问题出现。
选在哪重不重要？对做题结果会不会有影响？为什么要常常选择无限远处作为零电势点？这样选择与大地为零电势点有什么关系？等等，这些一系列的问题，都是我们研讨以及互相学习交流查阅资料等等的重点。
虽然在以前的大学物理课程中，电场与磁场等章节有学过相类似内容，但是，通过自主学习的过程，我们对此类问题又有了更深入的了解。
空腔，静电屏蔽，带电体，导体等一系列的名词，都在我们的研讨中出现，使我们有了更深刻的理解与联系。
通过讨论与分析，我们将这个课题主要分成了三个部分，并且穿插了相关例题，以便于理解以及应用。
总而言之，通过这次对静电场的研究，不仅增加了我们这方面的知识，也使我们的自学能力有所提高。
同时，小组合作分工，资料查阅，也使我们在课题研讨方面的能力有一定的提高。
这样，把以前的知识运用到题目中，并且学到了新的相关知识，使我们收获很大。
【参考文献】1、余恬，雷虹. 电磁场分析中的应用数学[M] . 北京邮电大学出版色, 2009.2、谢桂香. 静电场电势零点的选择[J] . 长春师范学院学报, 2007( 2 ), 26( 1 )。
3、邵小桃，李一枚.电磁场与电磁波基本教程.第一版.中国铁道出版社，2010.9。
