2.1.1指数与指数幂的运算(二)
- 格式:pdf
- 大小:1.29 MB
- 文档页数:14




§2.1.1指数与指数幂的运算(2)学习目标1. 理解分数指数幂的概念;2. 掌握根式与分数指数幂的相互转化; 3 掌握有理数指数幂的运算.预习案预习课本P 50—P 52 页内容 1.正数a 的正分数指数幂=n ma (),,0*N n m a ∈> 2.正数a 的负分数指数幂=-nm a(),,0*N n m a ∈>3.s r a a ⋅= (其中),,0Q s r a ∈> 4.s r a )( = (其中),,0Q s r a ∈> 5.s b a )(⋅= (其中),0,Q s b a ∈> 预习自测1. 求下列各式的值:(1)328 (2)21100-(3)239-2.用分数指数幂的形式表示并计算下列各式(式中字母都是正数):(1)a a ⋅2 (2)323a a ⋅ (3)a a3.计算下列各式(式中字母都是正数):(1)(2a 32b 21)(-6a 21b 31)÷(-3a 61b 65); (2)(m 41n 83-)8.我的疑问探究案自主探究一:(1)观察以下式子,并总结出规律:a >0,①510a =552)(a =a 2=a 510; ②8a =24)(a =a 4=a 28; ③412a =443)(a =a 3=a 412; ④210a =225)(a =a 5=a 210. (2)利用(1)的规律,你能表示下列式子吗?435,357,57a ,n m x (x>0,m,n∈+N ,且n>1).(3)你能用方根的意义来解释(3)的式子吗?(4)0的正分数指数幂等于多少?0有负指数幂吗? (5)负整数指数幂的意义是怎样规定的?合作探究例1. 已知231211322[()()]a b a b ab a ------==求的值.变题1:已知31=+-x x ,求下列各式的值:(1)2121-+x x例2. 比较63123,11,5的大小.例3.求下列各式的值:(1)432981⨯; (2)23×35.1×612.总结提升※ 学习小结:1. 分数指数幂nm a 不可理解为nm个a 相乘,它是根式的一种新写法 2. 0的正分数指数幂是0,0的负指数幂没有意义3. 负数的分数指数幂是否有意义,应视指数的分子、分母的具体数值而定※ 当堂检测: 1. 235.0322901.0)833(5.1)8.1(+-⋅+---=2. 求下列各式的值(其中各式字母均为正数):(1)23)425(-= ; (2)()551.0-=__________;(3)()24-π=________ (4)()66y x -()y x >=_______;(5)834121-a a a = ; (6)3163)278(--ba =3. 用根式的形式表示下列各式(a >0)(1).21a (2).43a (3).53-a(4).32-a训练案1. 计算下列各式的值: (1)[(a 23-b 2)-1·(ab -3)21(b 21)7]31(2)1112121-+-++--a a a aa(3)14323)(---÷a b b a2.用分数指数幂表示下列各式(1).32x (2).43)(b a + (3).4)(n m - (4).mm 33.下列运算中,正确的是( )A .a 2·a 3=a 6B .(-a 2)3=(-a 3)2C .(a -1)0=0 D .(-a 2)3=-a 64.下列各式①42)4(n -,②412)4(+-n ③54a ,④45a (各式的n∈N ,a∈R )中,有意义的是( )A.①②B.①③C.①②③④D.①③④5. 设x 5=4,y 5=2,则y x -25=________.思考题:设n n n x x a a x a )1(),(21,0211++-=>-求的值.。

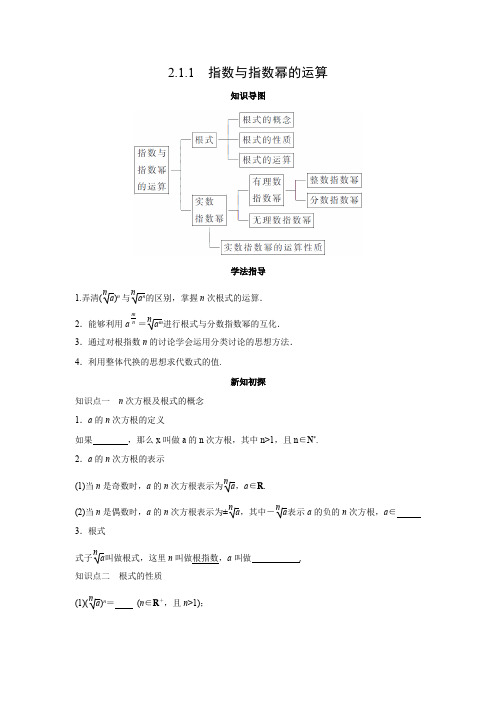
2.1.1 指数与指数幂的运算(2课时)第一课时 根式教案目标:1.理解n 次方根、根式、分数指数幂的概念;2.正确运用根式运算性质和有理指数幂的运算性质;3.培养学生认识、接受新事物和用联系观点看问题的能力。
教案重点:根式的概念、分数指数幂的概念和运算性质教案难点:根式概念和分数指数幂概念的理解教案方法:学导式教案过程:(I )复习回顾引例:填空 *)n a a a n N ⋅∈个(; m n a += (m,n ∈Z); _____=; (II )讲授新课1.引入:(1)填空(1),(2)复习了整数指数幂的概念和运算性质(其中:因为m na a ÷可看作m n a a -⋅,所以m n m n a a a -÷=可以归入性质m n m n a a a +⋅=;又因为n ba )(可看作m na a -⋅,所以n nn b a b a =)(可以归入性质()n n n ab a b =⋅(n ∈Z)),这是为下面学习分数指数幂的概念和性质做准备。
为了学习分数指数幂,先要学习n 次根式(*N n ∈)的概念。
(2)填空(3),(4)复习了平方根、立方根这两个概念。
如:分析:若22=4,则2叫4的平方根;若23=8,2叫做8的立方根;若25=32,则2叫做32的5次方根,类似地,若2n =a ,则2叫a 的n 次方根。
由此,可有:2.n 次方根的定义:(板书)问题1:n 次方根的定义给出了,x 如何用a 表示呢?n a x =是否正确? 分析过程:解:因为33=27,所以3是27的3次方根;因为5)2(-=-32,所以-2是-32的5次方根;因为632a )a (=,所以a 2是a 6的3次方根。
结论1:当n 为奇数时(跟立方根一样),有下列性质:正数的n 次方根是正数,负数的n 次方根是负数,任何一个数的方根都是唯一的。
此时,a 的n 次方根可表示为n a x =。
从而有:3273=,2325-=-,236a a =解:因为4216=,16)2(4=-,所以2和-2是16的4次方根;因为任何实数的4次方都是非负数,不会等于-81,所以-81没有4次方根。