外掠平板湍流边界层对流传热特性解析预测方法

大气边界层湍流热输运特性研究大气边界层是地球表面与大气中最接近地面的一层，它是气象学、地球物理学和环境科学中非常重要的研究对象。

湍流是大气边界层中的重要现象，它对热传输起着决定性的作用。

本文将探讨大气边界层湍流热输运的特性。

一、湍流热传输概述湍流热传输是指在流体中的湍流运动过程中，伴随着热量的传输。

大气边界层中的湍流主要发生在对流层和辐射层之间的过渡区域，其特点是速度与温度的涨落。

湍流热传输在大气边界层中起着重要的作用，直接影响着气候、气象、环境等多个方面。

二、湍流热传输的起源湍流热传输的起源可以追溯到大气运动的各种驱动力，包括地球自转、太阳辐射、地形和大尺度气候系统等。

这些驱动力相互作用，生成了大气边界层中的不稳定运动。

这种不稳定运动通过涡旋的形式传输能量和热量，形成湍流热传输。

三、湍流热传输特性的观测与研究方法想要深入研究大气边界层湍流热传输特性，首先需要获得准确的观测数据。

常用的观测方法包括航空器观测、气象测量仪器、卫星遥感和数值模拟等。

这些方法可以提供湍流运动的速度、温度和湍流强度等关键参数。

四、湍流热传输特性的影响因素湍流热传输特性受到多个因素的影响，其中包括大气稳定度、地表条件、季节变化、气团间的相互作用等。

较强的大气不稳定性会导致湍流活动增强，从而增加热传输。

地表条件的差异和季节变化也会对湍流热传输特性产生显著影响。

五、湍流热传输特性的意义和应用对大气边界层湍流热传输特性的研究具有重要的意义和广泛的应用价值。

首先，它有助于我们更好地了解大气运动和能量平衡机制，为气象预测和气候变化研究提供依据。

其次，对湍流热传输特性的深入认识有助于设计城市规划、农田排水和建筑物排烟等工程项目。

最后，湍流热传输特性的研究还可以改善工业生产和航空航天等领域的技术和流程。

六、未来的研究方向尽管我们对大气边界层湍流热传输特性已经取得了一定的研究进展，但仍然存在许多未解之谜和挑战。

未来的研究可以从多个角度进行，如深入探索湍流热传输与偏差之间的关系、开展更精确的大气运动观测以及利用新技术手段提高湍流热传输预测能力等。

外掠平板湍流边界层对流传热特性解析预测方法引言：外掠平板湍流边界层对流传热特性研究对于航空航天领域具有重要的意义。

对流传热特性的准确解析预测可以帮助我们更好地设计和优化外掠平板的结构，提高其传热性能。

本文将介绍几种常见的外掠平板湍流边界层对流传热特性解析预测方法。

一、湍流模型湍流模型是研究湍流边界层对流传热特性的重要工具，常见的湍流模型包括RANS（雷诺平均应力方程）、LES（大涡模拟）和DNS（直接数值模拟）等。

RANS是最常用的湍流模型，其基本假设是湍流边界层与速度/温度脉动之间存在统计相关性，适用于大多数工程问题。

LES则更加适用于高雷诺数湍流边界层的研究，可以更准确地捕捉湍流结构和湍流能量传输过程。

DNS则是最精确的湍流模型，通过数值方法直接求解湍流方程，能够提供最准确的湍流边界层对流传热特性。

二、湍流边界层模型湍流边界层模型是一种数学模型，用于描述边界层中湍流的空间和时间分布。

常见的湍流边界层模型包括Prandtl-Kármán模型和Cebeci-Smith模型等。

Prandtl-Kármán模型是最古老的湍流边界层模型，它假设边界层中的湍流速度分布服从对数规律，适用于平板流动的湍流边界层研究。

Cebeci-Smith模型是基于湍流边界层的涡旋结构提出的模型，适用于三维流动的湍流边界层研究。

三、流动数值模拟方法流动数值模拟方法是基于流体力学原理和数值计算技术，通过求解流动方程和湍流方程来模拟流动现象。

在外掠平板湍流边界层对流传热特性的解析预测中，常见的数值模拟方法包括有限差分方法、有限元方法和有限体积方法等。

这些方法可以通过离散化流动方程和湍流方程，将连续的流动问题转化为离散的数值问题，并通过数值计算方法求解。

四、实验方法实验方法是研究外掠平板湍流边界层对流传热特性的重要手段，可以通过实验证实和验证理论模型的准确性。

常见的湍流边界层对流传热实验方法包括热电偶法、红外热像法和激光测速法等。

外掠平板层流流动边界层微分方程积分解的实现
这是一篇关于外掠平板层流流动边界层微分方程积分解的文章。

平板层流是一种特殊的流动，通常表示流体在一个平板的表面上沿一个定向移动。

为了模拟这种平板层流，国际学术界将它划分为多个区域，每个区域都尝试研究由方程式描述的流动现象。

在这些研究中，外掠流动边界层微分方程经常被用于描述平板层流的行为。

外掠流动边界层微分方程实际上是一组常微分方程，这些方程反映了关于一个二维流动的平板表面上的流体质量和温度分布的矩阵。

平板层流中发生的一些物理过程都可以用这组方程来描述。

例如，当一个热流体流经一个冷却器时，可以使用外掠流动边界层微分方程来计算流体的温度和物质的分布状态。

要解决外掠流动边界层微分方程，需要在一定的假设和条件下定义流体行为，并使用数值积分技术来求解出结论。

数值积分需要使用特殊的积分来反映模型，而且在这个过程中需要按照某种方式将流体行为表示为均匀的网格，以便有助于求解数值解。

对外掠流动边界层微分方程求解的结果有多个应用场景。

例如，它可以用来计算污染物在水中传播的速度和深度，可以计算汽车在路面的摩擦力，也可以用来研究太阳能表面的热传导。

基于外掠流动边界层微分方程的求解还能够帮助开发新型工业化工装置，例如操作过程仿真，火力发电厂喷气推进动力系统等。

外掠流动边界层微分方程是非常有用的，在很多领域都有应用，但是在求解模型时，仍面临许多技术问题。

尽管在未来有许多改进的模型和技术，但这个模型必须经过精心的研究，才能够充分利用它的有用性。

只有这样，科学家和工程师才能够最大程度地利用这个模型来改善工业过程和工业设施的性能。

对于外掠平板的流场与换热的数值模拟，这里将简要介绍本例的关键要点，其他详细内容可参考书本。

1．求解器设置
这里选择SIMPLEC求解方法，SIMPLEC算法与SIMPLE算法的基本思路一致，仅在通量修正方法上有所改进，因而加快了计算的收敛速度。

SIMPLEC算法为求解非复杂问题时比较好的选择，使用SIMPLEC算法时，压力耦合算法的欠松弛因子一般应设为1.0，这样能加快收敛。

2．离散格式的选择
在用结构网格计算旋转流动问题时，QUICK格式可以提供更高的计算精度，但是在其他情况下，QUICK格式的精度与二阶格式相当，并没有很大的改进。

对于与流动方向对齐的结构网格而言，QUICK格式将可产生比二阶迎风格式等更精确的计算结果，因此，QUICK格式常用于六面体（或二维问题中的四边形）网格。

对于其他类型的网格，一般使用二阶迎风格式。

如上所述这里选用QUICK格式。

3．Monitors相关设置
默认设置中所有的变量残差都被监视，并在迭代过程中确认其是否满足收敛标准。

收敛将在满足变量的收敛标准后实现。

默认的收敛标准是除能量能量、辐射等方程的收敛标准是
6
10-外，其他变量的收敛标准均为3
10-。

一般而言当选择高阶离散格式时，可将上述标准10-，得到严格的收敛标准。

全部调整至6
4．创建等值面及等值面上的点
为了得到努赛尔数和沿平面方向上的壁面摩擦系数的图，用户应创建沿平板长度方向上的等值面，具体设置在此不再详述。

5．相关参数报告
在Report选项卡中有相关内容，具体设置可参考书本内容。

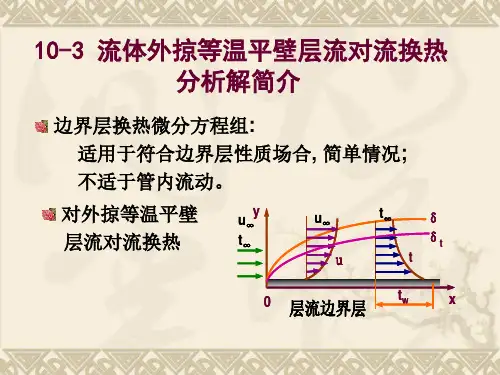
对流传热与传质期末复习题 请主要3－2、10－2和17题1、结合外掠平壁层流对流换热的求解，试述由边界层控制方程得到精确解和利用边界层积分方程式得到近似解两种方法的主要步骤、特点并比较其结果。

答：对于外掠平壁层流对流换热，由边界层控制方程得到精确解的主要步骤为：先根据外掠平壁流动的边界层动量方程和连续性方程，运用相似变换用流函数将动量方程转化为常微分方程，根据相应的边界条件就可得到速度分布的精确解，在求出速度分布的基础上，根据能量方程式和相应的边界条件即可得到温度分布的精确解，从而得到壁面热流和局部换热系数。

特点是：由边界层动量方程式得到的精确解，它的解依赖于速度分布的具体形式，且只适用于Re>>1的情况，不适用于进口导边附近的区域。

而利用边界层积分方程式得到近似解的主要步骤为：首先假定能满足有关边界条件的无量钢温度分布，在u ∞、t w 和t ∞都是常数的假定下，根据低速定物性流体外掠平壁的焓厚度定义式进行积分，可得到焓厚度及其沿轴向变化，壁面热流即可求出，进一步可得到换热系数。

其特点在于用边界层积分方程式进行求解，它的解并不十分依赖于速度分布的具体形式，且工作量小，简便。

结果比较：两种方法得到的解结果完全一致。

2、同样是层流对流换热，为什么外掠平壁的Nu ～Re 1/2，而管内充分发展的则h X ＝常数？ 答：流体外掠平壁时，从进口处形成速度边界层和热边界层，且随着流体的往前推进而逐渐增厚，到一定距离后会发生层流到紊流的过渡，不会象管内流动那样出现充分发展区，热流密度也不是常数而是和x有关，即('(0)w w q t t λ∞=-，因此局部换热系数w x w q h t t ∞=-，局部努谢尔数()w w q xNu t t λ∞=-，所以可得'(0)Nu θ=，即Nu ～Re 1/2；流体在管内作层流换热时，在充分热发展区，流体的无量纲温度分布不沿流体的推进方向而变化，只是r 的函数，管壁处沿径向的无量纲温度梯度r r rθ=∂∂也不推进方向变化，即w r r m w r rt t rr t t θ==⎛⎫-∂∂=⎪∂∂-⎝⎭＝常数，而壁温t w 和流体的混合平均温度t m 不随径向距离r 变化，而换热系数是用壁温和流体混合平均温度之差来定义的，即0w r r w m w m q th t t t t rλ=∂==---∂，显然为常数。

流体力学中的流体中的湍流边界层传热在流体力学中，流体的湍流边界层传热是一个重要且复杂的研究领域。

湍流边界层传热现象不仅在自然界中普遍存在，而且在工程和科学领域中也具有广泛的应用。

本文将从湍流边界层传热的概念、特征及其影响因素等方面进行论述。

一、湍流边界层传热的概念湍流边界层传热是指在流体运动中，当流速达到一定阈值时，流体会在固体表面形成湍流，从而增强固体表面与流体之间的传热效果。

湍流边界层传热的主要机制包括湍流速度场的非均匀性和湍流涡的产生与传递。

湍流边界层传热除了在大气中的天气系统中起着重要作用外，还广泛应用于航空、电子、能源等领域中。

例如，飞机的气动性能和发动机的热力特性都与湍流边界层传热密切相关。

二、湍流边界层传热的特征湍流边界层传热具有以下几个显著的特征：1. 高传热强度：湍流边界层传热时，相较于层流传热，能够实现更高的传热效果。

湍流的非均匀性使得热量能够更快地从固体表面传递到流体中。

2. 非线性：湍流边界层传热是一个高度非线性的过程，其传热特性受到很多因素的影响，如湍流强度、壁面条件以及湍流尺度等。

因此，湍流边界层传热的研究和模拟都需要考虑这些非线性因素。

3. 局部尺度效应：湍流边界层传热时，流体与固体表面之间的传热效果通常在边界层内部最强。

在离壁面距离较远处，流体的传热效果会逐渐减弱。

4. 温度剖面的不均匀性：在湍流边界层传热过程中，流体温度呈现明显的剖面变化。

通常，在流体靠近固体表面时，温度梯度较大，而在边界层外部，温度梯度则较小。

三、湍流边界层传热的影响因素湍流边界层传热受到多个因素的综合影响，其中最主要的影响因素包括以下几个：1. 流体性质：流体的性质直接影响湍流边界层传热的强度和特性。

不同流体的传热性能不同，如粘度、热导率等。

2. 壁面条件：固体表面的状态对湍流边界层传热起着重要作用。

不同的壁面条件会改变流体与固体之间的摩擦和传热特性，如粗糙度、表面温度等。

3. 湍流强度：湍流的强度直接决定了湍流边界层传热的强度。