八上人教版思维导图

你现在的努力要对得起别人对你的好！
Math 实验室-1-人教版八年级数学上册章节思维导图
共5章
人教版八年级数学上册教材目录
第11章三角形的思维导图
11.1与三角形有关的线段
11.2与三角形有关的角
11.3多边形及其内角和
第12章全等三角形的思维导图
12.1全等三角形
12.2三角形全等的判定
12.3角的平分线的性质
第13章轴对称的思维导图
13.1轴对称
13.2画轴对称图形
13.3等腰三角形
13.4课题学习最短路径问题
第14章整式的乘法与因式分解的思维导图
14.1整式的乘法
14.2乘法公式
14.3因式分解
第15章分式的思维导图
15.1分式
15.2分式的运算
15.3
分式方程。

人教版八年级上生物思维导图一、生物的基本特征1. 生物需要营养2. 生物能够进行呼吸3. 生物能排出体内产生的废物4. 生物能够对外界刺激作出反应5. 生物能够生长和繁殖6. 生物都有遗传和变异的特性7. 除病毒外，生物都是由细胞构成的二、生物的分类1. 病毒2. 原核生物3. 真核生物三、生物圈1. 生物圈的概念2. 生物圈的范围3. 生物圈与人类的关系四、生物与环境1. 环境的概念2. 环境的因素3. 生物对环境的适应4. 生物对环境的影响五、生物的多样性1. 生物多样性的概念2. 生物多样性的价值3. 生物多样性的保护六、生物的进化1. 进化的概念2. 进化的证据3. 进化的过程4. 人类在进化中的地位七、生物技术1. 生物技术的概念2. 生物技术的应用3. 生物技术的发展趋势八、生物学的研究方法1. 观察法2. 实验法3. 调查法4. 分类法九、生物学与人类生活1. 生物学与农业2. 生物学与医药3. 生物学与环境保护4. 生物学与人类健康人教版八年级上生物思维导图一、生物的基本特征1. 生物需要营养：生物体通过摄取营养物质来维持生命活动。

2. 生物能够进行呼吸：生物体通过呼吸作用获取能量。

3. 生物能排出体内产生的废物：生物体通过排泄作用将废物排出体外。

4. 生物能够对外界刺激作出反应：生物体通过感觉器官和神经系统对外界刺激作出反应。

5. 生物能够生长和繁殖：生物体通过生长和繁殖来延续物种。

6. 生物都有遗传和变异的特性：生物体通过遗传和变异来适应环境。

7. 除病毒外，生物都是由细胞构成的：细胞是生物体的基本单位。

二、生物的分类1. 病毒：病毒是一种非细胞结构的微生物，需要寄生在宿主细胞内才能生存。

2. 原核生物：原核生物是一类单细胞生物，没有细胞核和细胞器。

3. 真核生物：真核生物是一类多细胞生物，具有细胞核和细胞器。

三、生物圈1. 生物圈的概念：生物圈是地球上所有生物和它们生存环境的总和。

最新人教版《道德与法治》八年级上册-全册思维导图第一单元：道德修养与人生追求1.1 道德修养与社会道德• 1.1.1 道德修养的基本内涵–守法意识–民主意识–公德意识–奉献精神• 1.1.2 社会道德–概念–内容–作用1.2 理想追求与实践• 1.2.1 理想的概念–个人理想–社会理想• 1.2.2 理想追求与实践–实现理想的必要条件–实践的作用与重要性–理想追求中的困难与挫折及解决方法1.3 保持健康追求幸福• 1.3.1 保持健康的重要性–身体健康与心理健康的关系–保持健康的途径• 1.3.2 追求幸福的内涵–幸福的含义–幸福的来源–幸福感的培养方法第二单元：人生价值与人生观2.1 人生的价值与意义• 2.1.1 人生的价值–生命的固有价值–个体的实践价值–社会的发展价值• 2.1.2 人生的意义–个体意义与社会意义的关系–不同人生观的意义观2.2 人生观的塑造与价值追求• 2.2.1 人生观的形成–家庭环境的影响–同伴圈子的影响–学校教育的影响• 2.2.2 价值观的追求–理性追求与盲目追求–追求真善美的价值观2.3 发挥作用共创美好人生• 2.3.1 发挥作用的重要性–个体作用与社会发展的关系–合作共赢的理念• 2.3.2 如何发挥作用–尊重他人作用–发现与发展自己的作用–积极参与社会实践第三单元：学会自我保护3.1 我的安全，我的责任• 3.1.1 安全意识的培养–安全意识的重要性–安全意识的培养方法• 3.1.2 安全防范的基本知识–交通安全–火灾、电器用电安全–食品安全3.2 学会维权与自我保护• 3.2.1 维护自身合法权益的主要途径–监督举报–媒体维权–诉讼维权• 3.2.2 自我保护的基本原则与方法–防范陌生人侵害–遇到突发事件时的处理方法3.3 网络安全与信息保护• 3.3.1 网络安全意识–建立正确的网络安全观–防范网络欺诈与网络犯罪• 3.3.2 个人信息保护–主动保护个人信息–防范个人信息泄露第四单元：法治与人权4.1 法律与法治• 4.1.1 法律的作用与功能–维护社会秩序–保护人民权益–规范社会行为• 4.1.2 法治的内涵与特征–法律面前人人平等–法律的公正性与公平性4.2 人权的保障与促进• 4.2.1 人权的含义与特点–自由权利–平等权利–人权的可分割性与普遍性• 4.2.2 人权的保障与促进–国家机构的保障–全球人权保障机制4.3 法治教育与公民素质提升• 4.3.1 法治教育的重要性–法治教育的目的与意义–法治教育的内容与方法• 4.3.2 公民素质的提升–公民素质的内涵–提升公民素质的途径第五单元：社会责任与法律意识5.1 社会责任的内涵与作用• 5.1.1 社会责任的概念–个体的社会责任–团体的社会责任• 5.1.2 社会责任的作用–促进社会和谐稳定–推动社会发展5.2 法律意识与法治精神• 5.2.1 法律意识的培养–法律意识的重要性–法律意识的培养途径• 5.2.2 法治精神的内涵与培养–法治精神的特点与意义–法治精神的培养方法5.3 学会自我约束与社会监督• 5.3.1 自我约束的作用与方法–自我反省与自我改进–遵纪守法与自我约束• 5.3.2 社会监督的重要性与途径–媒体的监督作用–NGO与群众监督以上是最新人教版《道德与法治》八年级上册的全册思维导图。

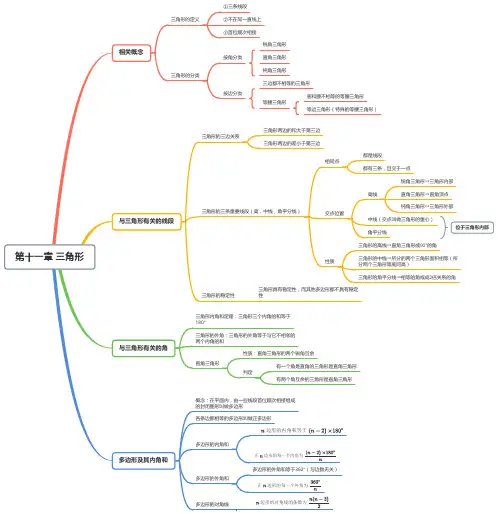
第十一章 三角形与三角形有关的线段与三角形有关的角多边形及其内角和相关概念三角形的定义三角形的分类三角形的三边关系①三条线段②不在同一直线上③首位顺次相接按角分类锐角三角形直角三角形钝角三角形按边分类三边都不相等的三角形等腰三角形底和腰不相等的等腰三角形等边三角形（特殊的等腰三角形）三角形两边的和大于第三边三角形两边的差小于第三边三角形的三条重要线段（高，中线，角平分线）相同点都是线段都有三条，且交于一点交点位置高线锐角三角形→三角形内部直角三角形→直角顶点钝角三角形→三角形外部 中线（交点叫做三角形的重心）角平分线位于三角形内部性质三角形的高线→直角三角形或90°的角 三角形的中线→所分的两个三角形面积相等（所分两个三角形等底同高）三角形的角平分线→相等的角或成2倍关系的角三角形的稳定性 三角形具有稳定性，而其他多边形都不具有稳定性 三角形内角和定理：三角形三个内角的和等于180° 三角形的外角：三角形的外角等于与它不相邻的两个内角的和直角三角形性质：直角三角形的两个锐角互余判定有一个角是直角的三角形是直角三角形有两个角互余的三角形是直角三角形 概念：在平面内，由一些线段首位顺次相接组成的封闭图形叫做多边形多边形的内角和多边形的外角和各条边都相等的多边形叫做正多边形边形的内角和等于正边形的每一个内角为多边形的外角和等于360°（与边数无关）正边形的每一个外角为多边形的对角线边形的对角线的条数为第十三章轴对称轴对称用坐标表示轴对称有关概念线段的垂直平分线轴对称图形的有关性质轴对称图形：把一个平面图形沿着一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形成轴对称：把一个图形沿着一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线（成轴）对称定义：经过线段中点并且垂直于这条线段的直线性质判定：与线段两个端点距离相等的点在这条线段的垂直平分线上对应线段相等，对应角相等对称轴垂直平分连接对应点的线段关于x轴对称的两个点的坐标特征：横坐标相等，纵坐标互为相反数关于y轴对称的两个点的坐标特征：横坐标互为相反数，纵坐标相等等腰三角形等腰三角形性质轴对称图形→有一条对称轴等边对等角→在同一个三角形中证明角相等三线合一顶角平分线底边上的高底边上的中线相互重合判定定义：两边相等等角对等边→也是证明线段相等的方法等边三角形性质轴对称图形→三条对称轴三线合一→三条三线合一的线三条边都相等三个内角都相等，并且每一个角都等于60°判定三条边相等的三角形→已知三边关系用此方法三个角都相等的三角形→已知三个内角的关系用此方法有一个角是60°的等腰三角形→已知两边相等时可找一个60°的角用此方法含30°角的直角三角形的性质：在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半应用“已知一条直线及其同侧的两点，在直线上确定一点，使它到这两个已知点的距离之和最小”的问题，这类问题一般都是首先作出其中一个点关于直线的对称点，然后连接另一点和对称点，借助两点之间线段最短解决问题线段垂直平分线垂直且平分该线段线段垂直平分线上任意一点到该线段两端点的距离相等三角形三条边的垂直平分线相交于一点，这一点到三个顶点的距离相等与线段两个端点距离相等的点在这条线段的垂直平分线上第十四章整式的乘法与因式分解幂的运算法则同底数幂的乘法法则：都是正整数推广：均为正整数逆用：都是正整数幂的乘方法则：都是正整数推广：都是正整数逆用：都是正整数积的乘方法则：都是正整数推广：都是正整数）逆用：都是正整数同底数幂的除法法则：都是正整数并且推广：都是正整数并且逆用：都是正整数并且零指数幂整式的乘、除法法则单项式乘单项式单项式乘多项式多项式乘多项式单项式除以单项式多项式除以单项式乘法公式平方差公式完全平方公式添括号因式分解提取公因式公式法系数×系数→积的系数同底数幂×同底数幂→积的幂只在一个单项式里含有的字母→连同指数作为积的一个因式法则：单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加公式表示：m(a+b-c)=ma+mb+m(-c)=ma+mb-m c法则：多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加公式表示：(a+b)(m-n)=am+a(-n)+bm+b(-n)=a m-an+bm-bn被除式系数÷除式系数→商的系数被除式同底数幂÷除式同底数幂→商中的幂只在被除式里含有的字母→连同指数作为商的一个因式法则：多项式除以单项式，先把这个多项式的每一项除以单项式，再把所得的商相加公式表示：(am+bm-cm)÷m=am÷m+bm÷m+(-c m)÷m=a+b+(-c)=a+b-c括号前“+”→括到括号里的各项都不变符号括号前“-”→括到括号里的各项都改变符号m a+mb+mc→m(a+b+c)公因式的确定方法系数→多项式中各项系数的最大公因数字母→多项式中各项中都含有的相同字母相同字母的次数→多项式中各项中相同字母的最低次幂第十五章分式分式的有关概念分式的基本性质分式方程分式的运算分式的定义分式有意义的条件分式值为零的条件基本性质约分和通分分式的乘法分式的除法分式的乘方分式的加减分式的混合运算分式方程的定义分式方程的解法分式方程的应用一般地如果表示两个整式并且中含有字母那么式子叫做分式分式无意义→B=0分式有意义→B≠0A=0B≠0缺一不可分式的式子与分母乘（或除以）同一个不等于0的整式，分式的值不变式子表示其中是整式分式的通分→确定最简公分母分式的约分→确定分子和分母的公因式最简公分母的确定方法系数→各分母系数的最小公倍数字母→各分母中含有的所有字母相同字母的次数→各分母中相同字母的最高次幂不等于不等于法则：是正整数逆用是正整数）同分母相加减：异分母相加减：无括号：乘方→乘除→加减有括号：小括号→中括号→大括号结果为最简形式负整数指数幂科学记数法绝对值小于1的数→为原数第个不为零的数字前面所有零的个数包括小数点前面的零分母中含有未知数的方程是分式方程，判断一个方程是否为分式方程关键看分母中是否含有未知数去分母→方程两边同乘最简公分母，把分式方程化为整式方程解整式方程检验→将整式方程的解代入最简公分母，如果最简公分母的值不为0，则整式方程的解使原分式方程的解；否则，就是原分式方程的增根，原分式方程无解审→审清题意，弄清已知量和未知量找→找出等量关系设→设未知数列→列分式方程解→解这个方程验→既要检验所求的解使分式方程的解，又要检验求得的解是否符合实际意义答→写出答案。