下载文档原格式
机器人机构学的数学基础
机器人机构学的数学基础包括向量、矩阵、三角函数、微积分等数学知识。
首先，向量是机器人机构学中必须掌握的概念，因为机器人的运动轨迹可以表示为一系列向量。
向量的长度和方向可以描述机器人的位置和姿态，因此对于机器人的运动规划和控制非常重要。
其次，矩阵是机器人机构学中不可或缺的数学工具，因为机器人的运动学和动力学问题可以表示为矩阵方程。
例如，通过矩阵变换可以将机器人末端执行器的位姿转换为关节角度，或者将关节力矩转换为末端执行器的力和力矩。
第三，三角函数也是机器人机构学中常用的数学工具，因为机器人的运动通常涉及到角度的变化。
例如，关节角度可以用正弦和余弦函数来表示，而逆解问题中也需要使用反三角函数求解。
最后，微积分是机器人机构学中的重要数学基础，因为机器人的运动学和动力学问题往往涉及到速度、加速度和力矩等概念。
例如，求解机器人的运动学和动力学模型时需要使用微积分知识，同时在机器人控制问题中也需要使用微积分来设计控制算法。
总之，机器人机构学的数学基础包括向量、矩阵、三角函数和微积分等数学知识。
掌握这些数学知识对于理解机器人的运动规划、控制和仿真非常重要。
![第2章 机器人运动学—数学基础[可打印版,含习题]](https://img.taocdn.com/s1/m/c5aed3c4a1c7aa00b52acbd8.png)
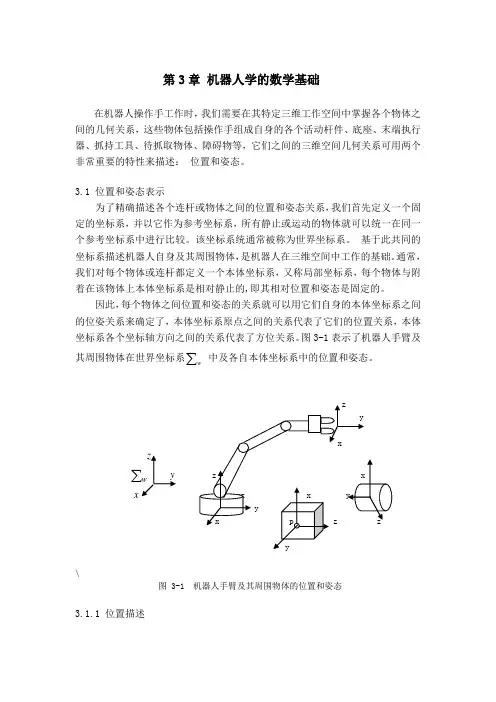
第3章机器人学的数学基础在机器人操作手工作时，我们需要在其特定三维工作空间中掌握各个物体之间的几何关系，这些物体包括操作手组成自身的各个活动杆件、底座、末端执行器、抓持工具、待抓取物体、障碍物等，它们之间的三维空间几何关系可用两个非常重要的特性来描述：位置和姿态。
3.1 位置和姿态表示为了精确描述各个连杆或物体之间的位置和姿态关系，我们首先定义一个固定的坐标系，并以它作为参考坐标系，所有静止或运动的物体就可以统一在同一个参考坐标系中进行比较。
该坐标系统通常被称为世界坐标系。
基于此共同的坐标系描述机器人自身及其周围物体，是机器人在三维空间中工作的基础。
通常，我们对每个物体或连杆都定义一个本体坐标系，又称局部坐标系，每个物体与附着在该物体上本体坐标系是相对静止的,即其相对位置和姿态是固定的。
因此，每个物体之间位置和姿态的关系就可以用它们自身的本体坐标系之间的位姿关系来确定了，本体坐标系原点之间的关系代表了它们的位置关系，本体坐标系各个坐标轴方向之间的关系代表了方位关系。
图3-1表示了机器人手臂及其周围物体在世界坐标系∑w中及各自本体坐标系中的位置和姿态。
zyxz∑W y z xx zzzzzz x yyx p z zy\图 3-1 机器人手臂及其周围物体的位置和姿态3.1.1 位置描述建立坐标系之后，三维空间中的任何一点都可以用一个具有三个分量的位置矢量来进行定位。
例如， 图3-1中立方体的质心p 在世界坐标系中的表示是：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=wz wy wx w p p p p下标w 代表了世界坐标系，因为位置矢量p 在不同坐标系中数值表示不同。
以上就是典型的基于笛卡尔坐标系的三维空间位置矢量的描述方法。
当采用不同的坐标系表示时，会有不同的位置描述方法。
例如 基于圆柱坐标系的空间矢量表示方法，基于球坐标系的空间矢量表示方法等。
3.1.2 方位描述机器人手臂工作时，不但要考虑所抓取的物体的质心的位置，还要考虑空间中该物体的姿态，既方位。
