当前位置：文档之家 › 《数学建模》实验四

《数学建模》实验四

  • 格式：doc
  • 大小：67.50 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

数学建模实验报告

数学建模实验报告

湖南城市学院数学与计算科学学院《数学建模》实验报告专业：学号：姓名：指导教师：成绩：年月日目录实验一 初等模型........................................................................ 错误！未定义书签。

实验二 优化模型........................................................................ 错误！未定义书签。

实验三 微分方程模型................................................................ 错误！未定义书签。

实验四 稳定性模型.................................................................... 错误！未定义书签。

实验五 差分方程模型................................................................ 错误！未定义书签。

实验六 离散模型........................................................................ 错误！未定义书签。

实验七 数据处理........................................................................ 错误！未定义书签。

实验八 回归分析模型................................................................ 错误！未定义书签。

实验一 初等模型实验目的：掌握数学建模的基本步骤，会用初等数学知识分析和解决实际问题。

实验内容：A 、B 两题选作一题，撰写实验报告，包括问题分析、模型假设、模型构建、模型求解和结果分析与解释五个步骤。

数学建模4

数学建模4
dN/dt=r（1-N/Nm）N即Logistic模型
当Nm与N相比很大时，rN2/Nm与rN相比可以忽略，则模型变为Malthus模型，即指数增长模型，但当Nm与N相比不是很大时，rN2/Nm这一项就不能忽略，但当人口很大时Malthus模型是不合理的。
用r（N）代替指数增长模型中的r，N（t0）=N0可推出如下：
>>y=101654*(1+0.0133).^x
y =
1.0e+005 *
Columns 1 through 11
1.0165 1.0301 1.0438 1.0576 1.0717 1.0860 1.1004 1.1150 1.1299 1.1449 1.1601
Columns 12 through 17
dx/dt=rx
x(0)=x0
由这个线性常系数微分方程容易解出:
x(t)=x0ert
表明人口将按指数规律无限增长(r>0)。将t以年为单位，上式表明，人口以er为公比的等比数列增长。因为这时r表示年增长率，通常r<<1，所以可用近似关系er≈1+r可得出
x(t)=x0(1+r)t即人口增长模型
>>x=0:16;
Columns 12 through 17
1.1742 1.1883 1.2022 1.2161 1.2299 1.2435
3.>>x=0:16;
>>y=101654*(1+0.0133).^x;
>>plot(x,y,'r')
>>hold on
>>x=0:16;
>>y1=[101654 103008 104357 105851 107507 109300 111026 112704 114333 115823 117171 118517 119850 121121 122389 123626 124810];

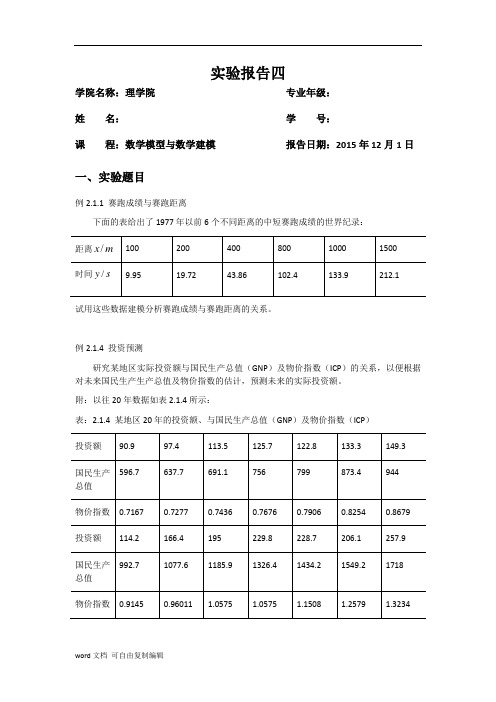
数学模型与数学建模-实验四

数学模型与数学建模-实验四

实验报告四学院名称：理学院专业年级：姓名：学号：课程：数学模型与数学建模报告日期：2015年12月1日一、实验题目例2.1.1 赛跑成绩与赛跑距离下面的表给出了1977年以前6个不同距离的中短赛跑成绩的世界纪录：试用这些数据建模分析赛跑成绩与赛跑距离的关系。

例2.1.4 投资预测研究某地区实际投资额与国民生产总值（GNP）及物价指数（ICP）的关系，以便根据对未来国民生产生产总值及物价指数的估计，预测未来的实际投资额。

附：以往20年数据如表2.1.4所示：表：2.1.4 某地区20年的投资额、与国民生产总值（GNP）及物价指数（ICP）二、实验目的针对问题解决的目标，对实际情况先有一个大概的估计。

随着信息量的增加，特别是数据的获取，就可以采用拟合模型与回归分析，或者采用插值模型与数值分析，使得到的结果更加丰富。

特别是，如果对表面现象产生的内在机理有所了解，就能够建立机理模型，则得到的结果更加科学靠谱。

这次实验主要介绍如何运用数学软件进行模型组建，并结合数学理论分析求解模型。

三、问题陈述第一题用所给数据数据建模分析赛跑成绩与赛跑距离的关系。

第二题研究某地区实际投资额与国民生产总值（GNP ）及物价指数（ICP ）的关系，以便根据对未来国民生产生产总值及物价指数的估计，预测未来的实际投资额。

四、模型及求解结果第一题共分4个步骤，分别叙述如下：步骤1 在坐标系上画出观测数据的散点图：步骤2 根据散点图，取线性拟合模型bx a y +=.步骤3 利用数据),(i i y x 估计模型参数b a ,.就是在寻找超定方程（方程个数多于未知量的个数）'y Ad =的近似解)',(b a d =，其中⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=n n y y y x x A 11',11称)',,,(21n x x x X =为设计矩形。

采用最小二乘法确定参数的估计值∧∧b a ,，也就是求拟合残差平方和21)(∑=--=ni i i bx a y Q的最小值点),(b a 。

数学建模实验四

数学建模实验四
Nonlinear variables: 0
Integer variables: 9
Total constraints: 10
Nonlinear constraints: 0
Total nonzeros: 38
Nonlinear nonzeros: 0
Variable Value Reduced Cost
问题三求解结果为目标函数值是16，此处6门课程分别是x1=x2=x3=x5=x7=x9=1，其余为零，学分最高为22，答案同问题二。
附录：
问题一程序
model:
min=x1+x2+x3+x4+x5+x6+x7+x8+x9;
x1+x2+x3+x4+x5>2;
x3+x5+x6+x8+x9>3;
x4+x6+x7+x9>2;
1 、以选课门数最少为目标建立选课策略数学规划模型。
2 、在选课门数最少的前提下，以学分最多为目标建立选课策略数学规划模型。
3 、既要选课门数少，又要学分多，建立2个目标的多目标规划模型，并用线性加权组合的方式将多个目标处理成一个新目标, 化为单目标规划进行求解。
问题分析与假设：
上述问题为数学规划中的多目标规划问题，可以建立0-1规划模型进行求解，设变量Xi表示课号，令Xi=1表示选课，Xi=0表示不选，然后根据题目建立目标函数和约束条件，最后用lingo软件求解。
对于第一个问题: 以选课门数最少为目标建立选课策略数学规划模型,可以直接列目标函数记为最小值求解；
对于第二个问题：在选课门数最少的前提下，以学分最多为目标建立选课策略数学规划模型，可以把问题一选课最少求解结果作为已知量再去建立学分最多目标函数记为最大值；

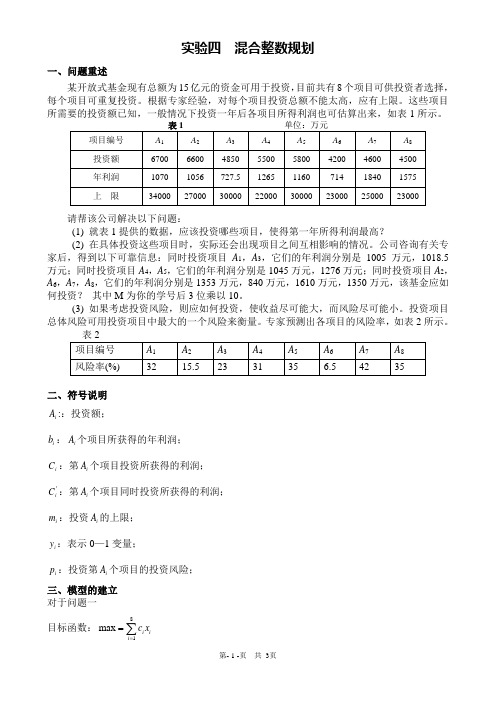
数学建模——混合整数规划

数学建模——混合整数规划

实验四 混合整数规划一、问题重述某开放式基金现有总额为15亿元的资金可用于投资，目前共有8个项目可供投资者选择，每个项目可重复投资。

根据专家经验，对每个项目投资总额不能太高，应有上限。

这些项目所需要的投资额已知，一般情况下投资一年后各项目所得利润也可估算出来，如表1所示。

请帮该公司解决以下问题：(1) 就表1提供的数据，应该投资哪些项目，使得第一年所得利润最高？(2) 在具体投资这些项目时，实际还会出现项目之间互相影响的情况。

公司咨询有关专家后，得到以下可靠信息：同时投资项目A 1，A 3，它们的年利润分别是1005万元，1018.5万元；同时投资项目A 4，A 5，它们的年利润分别是1045万元，1276万元；同时投资项目A 2，A 6，A 7，A 8，它们的年利润分别是1353万元，840万元，1610万元，1350万元，该基金应如何投资？ 其中M 为你的学号后3位乘以10。

(3) 如果考虑投资风险，则应如何投资，使收益尽可能大，而风险尽可能小。

投资项目总体风险可用投资项目中最大的一个风险来衡量。

专家预测出各项目的风险率，如表2所示。

二、符号说明i A :：投资额；i b ：i A 个项目所获得的年利润；i C ：第i A 个项目投资所获得的利润； 'i C ：第i A 个项目同时投资所获得的利润；i m ：投资i A 的上限； i y ：表示0—1变量；i p ：投资第i A 个项目的投资风险；三、模型的建立 对于问题一目标函数：81max i i i c x ==∑s.t. 150000i i i i i ib x b x m ⎧≤⎪⎨⎪≤⎩∑对于问题二 设定0—1变量131130...,1...,A A y A A ⎧⎨⎩项目不同时投资项目同时投资 452450...,1...,A A y A A ⎧⎨⎩项目不同时投资项目同时投资 2678326780...,,1...,,A A A A y A A A A ⎧⎨⎩,项目不同时投资,项目同时投资 目标函数：''''11133111332445524455''''322667788322667788max ()(1)()()(1)()()(1)()y x c x c y x c x c y x c x c y x c x c y x c x c x c x c y x c x c x c x c =++-++++-++++++-+++s.t. 11313124545232678267831500001000i i i i i ib x k y x xx x y ky x x x x y k y x x x x x x x x y kb x m ⎧≤⎪⎪=⎪⎪≤⎪⎪≥⎪⎪≤⎨⎪⎪≥⎪⎪≤⎪⎪≥⎪⎪≤⎩∑对于问题三：目标函数：max min max()i iii i i c x b x p =∑s.t. 150000i i i i i ib x b x m ⎧≤⎪⎨⎪≤⎩∑对于问题三模型的简化固定投资风险，优化收益，设a 为固定的最大风险。

数学模型实验四 综合实验

数学模型实验四 综合实验

实验四 综合实验一、 实验目的：通过实验小结，布置小型研究问题（经过数学处理），使学生在练习过程中进一步熟悉MATLAB的使用，以及深入理解数学模型的建模思想。

为后续课程设计教学环节构筑基础。

二、 预备知识：1.具备数学分析、常微分方程、运筹学和概率论的学科知识基础；2.相关学科知识的简单求解方法以及辅助MATLAB求解相关问题。

三、 实验内容及要求(任选一题完成)：1、黄河小浪底调水调沙问题2004 年6 月至7 月黄河进行了第三次调水调沙试验，特别是首次由小浪底、三门峡和万家寨三大水库联合调度，采用接力式防洪预泄放水，形成人造洪峰进行调沙试验获得成功。

整个试验期为20 多天，小浪底从6 月19 日开始预泄放水，直到7 月13 日恢复正常供水结束。

小浪底水利工程按设计拦沙量为75.5 亿m3，在这之前，小浪底共积泥沙达14.15 亿t。

这次调水调沙试验一个重要目的就是由小浪底上游的三门峡和万家寨水库泄洪，在小浪底形成人造洪峰，冲刷小浪底库区沉积的泥沙，在小浪底水库开闸泄洪以后，从6 月27 日开始三门峡水库和万家寨水库陆续开闸放水，人造洪峰于29日先后到达小浪底，7 月3 日达到最大流量2700m3/s，使小浪底水库的排沙量也不断地增加。

表7 是由小浪底观测站从6 月29 日到7 月10 检测到的试验数据。

现在，根据试验数据建立数学模型研究下面的问题：（1）给出估计任意时刻的排沙量及总排沙量的方法；（2）确定排沙量与水流量的关系。

2、炼油厂将A, B, C三种原油加工成甲、乙、丙三种汽油。

一桶原油加工成一桶汽油的费用为4元，每天至多能加工汽油14000桶。

原油的买入价、买入量、辛烷值、硫含量，及汽油的卖出价、需求量、辛烷值、硫含量由下表给出。

问如何安排生产计划，在满足需求的条件下使利润最大？一般说来，作广告可以增加销售，估计一天向一种汽油投入一元广告费，可使这种汽油日销量增加10桶，问如何安排生产和广告计划使利润最大？原油类别 买入价（元/桶） 买入量（桶/天）辛烷值硫含量（%）A 45 ≤5000 12 0.5B 35 ≤5000 6 2.0 C25≤50008 3.0汽油类别 卖出价（元/桶） 需求量（桶/天）辛烷值硫含量（%）甲 70 3000 ≥10 ≤1.0 乙 60 2000 ≥8 ≤2.0 丙501000≥6≤1.03、合金的强度y 与其中的碳含量x 有比较密切的关系，今从生产中收集了一批 数据如下表1。

数学建模实验4

beq=[2,1,1]';
L=1e-6.*ones(10,1);
U=inf.*ones(10,1);
x0=ones(10,1);
[x,fval]=fmincon('ex02',x0,[],[],Aeq,beq,L,U)
运行结果如下：
x=
0.3936
0.8032
0.0000
1.0000
0.0000
0.0000
若c变小，第一季度的生产量增加，第二季度不变，第三季度的生产量减少。C变大，第一季度生产量减少，第二季度不变，第三季度生产量增加。这是因为c变小，存储费用会变小，相对于生产费用的快速增长，最好的办法就是在生产费用低的时候多生产，把多余的机器进行存储，存储的费用会小于费用的增长额度，这样做可以节省生产费用，而c变大，情况正好相反。
建模分析：
设三季度分别生产X1,X2,X3台
目标函数：S=f（X1）+f（X2）+f（X3）+（X1-40）*C+(X2+X1-40-60)*C
约束条件：
X1>=40
X2+X1-40>=60
X3+X2+X1-40-60=80
X1<=100,
X2<=100,
X3<=100
MATLAB程序如下：
先编写M文件fun.m如下
vlb=[40;0;0];vub=[100;100;100];
[x,fval]=fmincon('fun',x0,A,b,Aeq,beq,vlb,vub)
运行结果为
x =
49.9999
60.0000
70.0000
fval =

数学建模上机实验4

[y,x]=find(bw);
以上程序可以求得图像中的所有边缘点坐标。
求解的Matlab程序代码：function shiyan 4()
%取出椭圆坐标
f=rgb2gray(imread('椭圆拟合原图test4.bmp'));
bw=edge(f,'sobel');
figure,imshow(bw)
[y,x]=find(bw);
%设出圆锥曲线方程
F=@(p,x)p(1)*x(:,1).^2+p(2)*x(:,1).*x(:,2)+p(3)*x(:,2).^2+p(4)*x(:,1)+p(5)*x(:,2)+p(6);
%离散数据点
x=[y,x]
p0=[1 1 1 1 1 1];
warning off
%拟合系数，最小二乘方法
p=nlinfit(x,zeros(size(x,1),1),F,p0);
title('曲线拟合');
legend('样本点','拟合曲线')
p
计算结果与问题分析讨论：
vv
拟合系数为：
p =
1.0e-029 *
0.0001 0.0000 0.0001 -0.0104 -0.0095 0.4561
bw=edge(f,'sobel');
figure,imshow(bw)
[y,x]=find(bw);
以上程序可以求得图像中的所有边缘点坐标。
问题的分析和假设：
采用最小二乘方法Байду номын сангаас拟合系数。
建模：
f=rgb2gray(imread('椭圆拟合原图.bmp'));

数学建模实验四：Matlab神经网络以及应用于汽油辛烷值预测

实验四：Matlab 神经网络以及应用于汽油辛烷值预测专业年级： 2014级信息与计算科学1班姓名： 黄志锐 学号：201430120110一、实验目的1. 掌握MATLAB 创建BP 神经网络并应用于拟合非线性函数2. 掌握MATLAB 创建REF 神经网络并应用于拟合非线性函数3. 掌握MATLAB 创建BP 神经网络和REF 神经网络解决实际问题4. 了解MATLAB 神经网络并行运算二、实验内容1. 建立BP 神经网络拟合非线性函数2212y x x =+第一步 数据选择和归一化根据非线性函数方程随机得到该函数的2000组数据，将数据存贮在data.mat 文件中（下载后拷贝到Matlab 当前目录），其中input 是函数输入数据，output 是函数输出数据。

从输入输出数据中随机选取1900中数据作为网络训练数据，100组作为网络测试数据，并对数据进行归一化处理。

第二步 建立和训练BP 神经网络构建BP 神经网络，用训练数据训练，使网络对非线性函数输出具有预测能力。

第三步 BP 神经网络预测用训练好的BP 神经网络预测非线性函数输出。

第四步 结果分析通过BP 神经网络预测输出和期望输出分析BP 神经网络的拟合能力。

详细MATLAB代码如下：27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54disp(['神经网络的训练时间为', num2str(t1), '秒']);%% BP网络预测% 预测数据归一化inputn_test = mapminmax('apply', input_test, inputps); % 网络预测输出an = sim(net, inputn_test);% 网络输出反归一化BPoutput = mapminmax('reverse', an, outputps);%% 结果分析figure(1);plot(BPoutput, ':og');hold on;plot(output_test, '-*');legend('预测输出', '期望输出');title('BP网络预测输出', 'fontsize', 12);ylabel('函数输出', 'fontsize', 12);xlabel('样本', 'fontsize', 12);% 预测误差error = BPoutput-output_test;figure(2);plot(error, '-*');title('BP神经网络预测误差', 'fontsize', 12);ylabel('误差', 'fontsize', 12);xlabel('样本', 'fontsize', 12);figure(3);plot((output_test-BPoutput)./BPoutput, '-*');title('BP神经网络预测误差百分比');errorsum = sum(abs(error));MATLAB代码运行结果截图如下所示：MATLAB代码运行结果如下所示：图1 BP神经网络预测输出图示图2 BP神经网络预测误差图示图3 BP 神经网络预测误差百分比图示2. 建立RBF 神经网络拟合非线性函数22112220+10cos(2)10cos(2)y x x x x ππ=-+-第一步 建立exact RBF 神经网络拟合, 观察拟合效果详细MATLAB 代码如下：MATLAB代码运行结果如下所示：图4 RBF神经网络拟合效果图第二步建立approximate RBF神经网络拟合详细MATLAB代码如下：13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41F = 20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2); %% 建立RBF神经网络% 采用approximate RBF神经网络。

数学建模作业 北工大薛毅 实验4

第四次作业解：(1) 平方和最小的目标方程：()2n 1i i i 10y -x min 10∑=+=ββββ，编程如下：model:sets:quantity/1..50/: x,y;endsetsmin=@sum(quantity: (B0+B1*x-y)^2);data:y=2 10 4 22 16 10 18 26 34 17 28 14 20 24 28 26 34 34 46 26 36 60 80 20 26 54 32 40 32 40 50 42 56 76 84 36 46 68 32 48 52 56 64 66 54 70 92 93 120 85;x=4 4 7 7 8 9 10 10 10 11 11 12 12 12 12 13 13 13 13 14 14 14 14 15 15 15 16 16 17 17 17 18 18 18 18 19 19 19 20 20 20 20 20 22 23 24 24 24 24 25;enddata@free(B0); @free(B1);End得到结果如下：Local optimal solution found.Objective value: 11353.52Infeasibilities: 0.000000Extended solver steps: 5Total solver iterations: 18Model Class: NLPTotal variables: 3Nonlinear variables: 2Integer variables: 0Total constraints: 2Nonlinear constraints: 1Total nonzeros: 3Nonlinear nonzeros: 2Variable Value Reduced CostB0 -17.57909 0.000000B1 3.932409 0.000000X( 1) 4.000000 0.000000X( 2) 4.000000 0.000000X( 3) 7.000000 0.000000X( 4) 7.000000 0.000000X( 5) 8.000000 0.000000X( 6) 9.000000 0.000000X( 7) 10.00000 0.000000X( 8) 10.00000 0.000000X( 9) 10.00000 0.000000X( 10) 11.00000 0.000000X( 11) 11.00000 0.000000 X( 12) 12.00000 0.000000 X( 13) 12.00000 0.000000 X( 14) 12.00000 0.000000 X( 15) 12.00000 0.000000 X( 16) 13.00000 0.000000 X( 17) 13.00000 0.000000 X( 18) 13.00000 0.000000 X( 19) 13.00000 0.000000 X( 20) 14.00000 0.000000 X( 21) 14.00000 0.000000 X( 22) 14.00000 0.000000 X( 23) 14.00000 0.000000 X( 24) 15.00000 0.000000 X( 25) 15.00000 0.000000 X( 26) 15.00000 0.000000 X( 27) 16.00000 0.000000 X( 28) 16.00000 0.000000 X( 29) 17.00000 0.000000 X( 30) 17.00000 0.000000 X( 31) 17.00000 0.000000 X( 32) 18.00000 0.000000 X( 33) 18.00000 0.000000 X( 34) 18.00000 0.000000 X( 35) 18.00000 0.000000 X( 36) 19.00000 0.000000 X( 37) 19.00000 0.000000 X( 38) 19.00000 0.000000 X( 39) 20.00000 0.000000 X( 40) 20.00000 0.000000 X( 41) 20.00000 0.000000 X( 42) 20.00000 0.000000 X( 43) 20.00000 0.000000 X( 44) 22.00000 0.000000 X( 45) 23.00000 0.000000 X( 46) 24.00000 0.000000 X( 47) 24.00000 0.000000 X( 48) 24.00000 0.000000 X( 49) 24.00000 0.000000 X( 50) 25.00000 0.000000 Y( 1) 2.000000 0.000000 Y( 2) 10.00000 0.000000 Y( 3) 4.000000 0.000000 Y( 4) 22.00000 0.000000Y( 5) 16.00000 0.000000 Y( 6) 10.00000 0.000000 Y( 7) 18.00000 0.000000 Y( 8) 26.00000 0.000000 Y( 9) 34.00000 0.000000 Y( 10) 17.00000 0.000000 Y( 11) 28.00000 0.000000 Y( 12) 14.00000 0.000000 Y( 13) 20.00000 0.000000 Y( 14) 24.00000 0.000000 Y( 15) 28.00000 0.000000 Y( 16) 26.00000 0.000000 Y( 17) 34.00000 0.000000 Y( 18) 34.00000 0.000000 Y( 19) 46.00000 0.000000 Y( 20) 26.00000 0.000000 Y( 21) 36.00000 0.000000 Y( 22) 60.00000 0.000000 Y( 23) 80.00000 0.000000 Y( 24) 20.00000 0.000000 Y( 25) 26.00000 0.000000 Y( 26) 54.00000 0.000000 Y( 27) 32.00000 0.000000 Y( 28) 40.00000 0.000000 Y( 29) 32.00000 0.000000 Y( 30) 40.00000 0.000000 Y( 31) 50.00000 0.000000 Y( 32) 42.00000 0.000000 Y( 33) 56.00000 0.000000 Y( 34) 76.00000 0.000000 Y( 35) 84.00000 0.000000 Y( 36) 36.00000 0.000000 Y( 37) 46.00000 0.000000 Y( 38) 68.00000 0.000000 Y( 39) 32.00000 0.000000 Y( 40) 48.00000 0.000000 Y( 41) 52.00000 0.000000 Y( 42) 56.00000 0.000000 Y( 43) 64.00000 0.000000 Y( 44) 66.00000 0.000000 Y( 45) 54.00000 0.000000 Y( 46) 70.00000 0.000000 Y( 47) 92.00000 0.000000 Y( 48) 93.00000 0.000000Y( 49) 120.0000 0.000000Y( 50) 85.00000 0.000000Row Slack or Surplus Dual Price1 11353.52 -1.000000 所以得到平方和最小时的β0为-17.57909，β1为3.932409。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Model Class: PILP
Total variables: 9
Nonlinear variables: 0
Integer variables: 9
Total constraints: 11
Nonlinear constraints: 0
Total nonzeros: 47
Nonlinear nonzeros: 0
Variable Value Reduced Cost
X1
X2
X3
X4
X5
X6
X7
X8
X9
Row Slack or Surplus Dual Price
1
2
3
4
5
6
7
8
9
10
11
精心搜集整理，只为你的需要
x1+x2+x3+x4+x5>2;
x3+x5+x6+x8+x9>3;
x4+x6+x7+x9>2;
2*x3-x1-x2<0;
x4-x7<0;
2*x5-x1-x2<0;
x6-x7<0;
x8-x5<0;
2*x9-x1-x2<0;
x1+x2+x3+x4+x5+x6+x7+x8+x9<6;
@bin(x1);@bin(x2);@bin(x3);@bin(x4);@bin(x5);@bin(x6);@bin(x7);@bin(x8);@bin(x9);
end
程序结果：
Global optimal solution found.
Objective value:
Objective bound:
Infeasibilities:
Extended solver steps: 0
Total solver iterations: 0
Elapsed runtime seconds:
end
程序结果：
Global optimal solution found.
Objective value:
Objective bound:
Infeasibilities:
Extended solver steps: 0
Total solver iterations: 0
Elapsed runtime seconds:
对于第一个问题: 以选课门数最少为目标建立选课策略数学规划模型,可以直接列目标函数记为最小值求解；
对于第二个问题：在选课门数最少的前提下，以学分最多为目标建立选课策略数学规划模型，可以把问题一选课最少求解结果作为已知量再去建立学分最多目标函数记为最大值；
对于第三个问题：既要选课门数少，又要学分多，就通过建立2个目标的多目标规划模型，并用线性加权组合的方式将多个目标处理成一个新目标, 化为单目标规划进行求解。
Global optimal solution found.
Objective value:
Objective bound:
Infeasibilities:
Extended solver steps: 0
Total solver iterations: 0
Model Class: PILP
Total variables: 9
问题三求解结果为目标函数值是16，此处6门课程分别是x1=x2=x3=x5=x7=x9=1，其余为零，学分最高为22，答案同问题二。
附录：
问题一程序
model:
min=x1+x2+x3+x4+x5+x6+x7+x8+x9;
x1+x2+x3+x4+x5>2;
x3+x5+x6+x8+x9>3;
x4+x6+x7+x9>2;
《数学建模》实验报告
实验序号： 实验四 日期： 2015年6月3日
班级
遥感1402班
姓名
郑永杰
学号
3
实验名称 整数规划与lingo程序设计 选课策略
实验目的：
1）学会lingo软件的基本使用方法。
2）加强学生对0-1变量的认识和理解；培养学生建模的能力。
3）了解多目标规划模型求解基本原理。
实验内容及要求：
X1
X2
X3
X4
X5
X6
X7
X8
X9
Row Slack or Surplus Dual Price
1
2
3
4
5
6
7
8
9
10
问题二程序：
model:
max=5*x1+4*x2+4*x3+3*x4+4*x5+3*x6+2*x7+2*x8+3*x9;
x1+x2+x3+x4+x5>2;
x3+x5+x6+x8+x9>3;
将以上目标函数和约束条件所建立的模型输入到lingo中求解（注意加上xi为0-1约束）
对于第二个问题，在选课最少的前提下，即选课门数为6，使得学分最高。目标函数即：
约束条件除问题一以上约束外再增加选课门数约束,即：
再次输入lingo求解
对于第三个问题，既要选课门数少，又要学分多，建立2个目标的多目标规划模型，并用线性加权组合的方式将多个目标处理成一个新目标, 化为单目标规划进行求解。所以建立目标函数为
x4+x6+x7+x9>2;
2*x3-2*x5-x1-x2<0;
x6-x7<0;
x8-x5<0;
2*x9-x1-x2<0;
x1+x2+x3+x4+x5+x6+x7+x8+x9<6;
@bin(x1);@bin(x2);@bin(x3);@bin(x4);@bin(x5);@bin(x6);@bin(x7);@bin(x8);@bin(x9);
2*x3-x1-x2<0;
x4-x7<0;
2*x5-x1-x2<0;
x6-x7<0;
x8-x5<0;
2*x9-x1-x2<0;
@bin(x1);@bin(x2);@bin(x3);@bin(x4);@bin(x5);@bin(x6);@bin(x7);@bin(x8);@bin(x9);
end
程序结果
Variable Value Reduced Cost
X1
X2
X3
X4
X5
X6
X7
X8
X9
Row Slack or Surplus Dual Price
1
2
3
4
5
6
7
8
9
10
11
3
4
5
6
7
8
9
10
11
问题三程序：
model:
max=4*x1+3*x2+3*x3+2*x4+3*x5+2*x6+1*x7+1*x8+2*x9;
Model Class: PILP
Total variables: 9
Nonlinear variables: 0
Integer variables: 9
Total constraints: 11
Nonlinear constraints: 0
Total nonzeros: 47
Nonlinear nonzeros: 0
模型的建立和求解：
用Xi=1表示选修表中按编号顺序的9门课程（Xi=0表示不选；i=1,2…，9）。问题的目标为选修的课程总数最少，即
约束条件包括两个方面：
第一，每人最少要学习2门数学课，3门运筹课和2门计算机课，根据表中对每门课程所属类别的划分，这一约束可以表示为：
第二，某些课程要有先修的要求，例如“数据结构”的先修课程“计算机编程”，意味着如果x4=1必须x7=1，可以表示为x4 x7，同里其他先修课程亦是如此。其中x1 x3，x2 x3可以用一个约束表示为2x3-x2-x1 0，故所有课程的先修课程要求可以表示为以下约束：
Nonlinear variables: 0
Integer variables: 9
Total constraints: 10
Nonlinear constraints: 0
Total nonzeros: 38
Nonlinear nonzeros: 0
Variable Value Reduced Cost
1 、以选课门数最少为目标建立选课策略数学规划模型。
2 、在选课门数最少的前提下，以学分最多为目标建立选课策略数学规划模型。
3 、既要选课门数少，又要学分多，建立2个目标的多目标规划模型，并用线性加权组合的方式将多个目标处理成一个新目标, 化为单目标规划进行求解。
问题分析与假设：
上述问题为数学规划中的多目标规划问题，可以建立0-1规划模型进行求解，设变量Xi表示课号，令Xi=1表示选课，Xi=0表示不选，然后根据题目建立目标函数和约束条件，最后用lingo软件求解。
约束条件如问题一，此处略。输入lingo后求解。
结果分析与检验：
问题一求解结果为x1=x2=x3=x6=x9=1，其他变量为0.对照编号，若使选课最少，可选择微积分，线性代数，最优化方法，计算机模拟，计算机编程，数学实验，共6门课程，总学分21.