DS证据理论
- 格式:doc
- 大小:2.23 MB
- 文档页数:36



《基于DS证据理论的多传感器数据融合算法研究与应用》篇一一、引言在众多复杂系统和智能技术中,数据扮演着至关重要的角色。
在现实生活中,很多场景都需要通过多传感器系统来获取和融合数据。
这些传感器可能会产生不同的数据类型和观点,如何有效地融合这些数据,提高系统的整体性能,就变得至关重要。
本文主要研究了基于DS(Dempster-Shafer)证据理论的多传感器数据融合算法。
通过分析该算法的理论基础,探究其在各种实际场景中的应用,以及面临的挑战和解决方案。
二、DS证据理论的基础DS证据理论是一种用于处理不确定性和不完全性问题的决策理论。
它通过组合多个证据或数据源的信息,来得出更全面、更准确的结论。
该理论基于概率论和信念函数,具有强大的数据处理能力。
在DS证据理论中,每个传感器或数据源都被视为一个独立的证据,它们提供的信息被视为一个假设空间中的不同假设的概率分布。
通过将这些概率分布进行组合,可以得到一个综合的假设概率分布,这就是我们所需的融合结果。
三、多传感器数据融合算法基于DS证据理论的多传感器数据融合算法主要包含以下几个步骤:1. 数据预处理:对各个传感器的数据进行清洗、转换和标准化处理,以便进行后续的融合处理。
2. 特征提取:从预处理后的数据中提取出有用的特征信息,这些特征信息将被用于后续的假设空间构建。
3. 假设空间构建:根据提取的特征信息,构建一个假设空间,每个假设对应一个可能的融合结果。
4. 概率分配:根据每个传感器或数据源提供的信息,将概率分配给每个假设。
这一步是DS证据理论的核心步骤。
5. 概率组合:通过DS组合规则,将各个传感器的概率分布进行组合,得到一个综合的假设概率分布。
6. 决策输出:根据综合的假设概率分布,得出最终的决策结果。
四、应用场景基于DS证据理论的多传感器数据融合算法在许多领域都有广泛的应用。
例如:1. 智能交通系统:通过融合来自摄像头、雷达、激光雷达等传感器的数据,提高车辆对环境的感知能力,从而提升交通系统的安全性和效率。

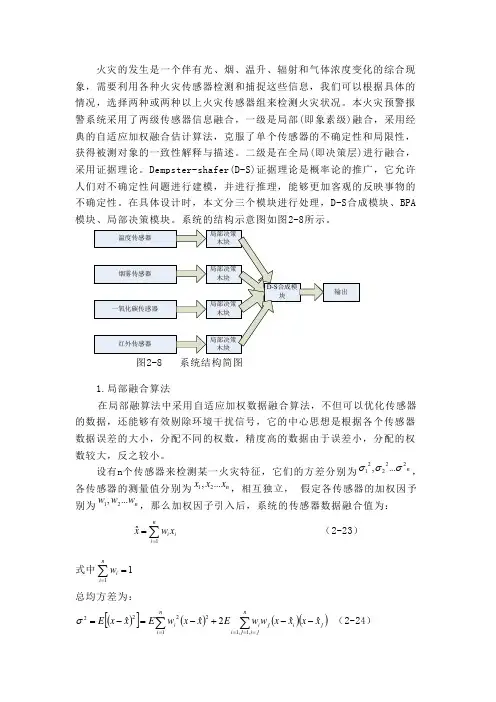
火灾的发生是一个伴有光、烟、温升、辐射和气体浓度变化的综合现象,需要利用各种火灾传感器检测和捕捉这些信息,我们可以根据具体的情况,选择两种或两种以上火灾传感器组来检测火灾状况。
本火灾预警报警系统采用了两级传感器信息融合,一级是局部(即象素级)融合,采用经典的自适应加权融合估计算法,克服了单个传感器的不确定性和局限性,获得被测对象的一致性解释与描述。
二级是在全局(即决策层)进行融合,采用证据理论。
Dempster-shafer(D-S)证据理论是概率论的推广,它允许人们对不确定性问题进行建模,并进行推理,能够更加客观的反映事物的不确定性。
在具体设计时,本文分三个模块进行处理,D-S 合成模块、BPA 模块、局部决策模块。
系统的结构示意图如图2-8所示。
图2-8 系统结构简图1.局部融合算法在局部融算法中采用自适应加权数据融合算法,不但可以优化传感器的数据,还能够有效剔除环境干扰信号,它的中心思想是根据各个传感器数据误差的大小,分配不同的权数,精度高的数据由于误差小,分配的权数较大,反之较小。
设有n 个传感器来检测某一火灾特征,它们的方差分别为n 22221...,σσσ,各传感器的测量值分别为n x x x ...,21,相互独立, 假定各传感器的加权因予别为n w w w ...,21,那么加权因子引入后,系统的传感器数据融合值为: ∑==ni i i x w x1ˆ (2-23) 式中11=∑=ni i w总均方差为:()[]()()()∑∑====--+-=-=ni nji j i jijii x x xx w w E x x w E xx E 1,1,12222ˆˆ2ˆˆσ (2-24)因为n x x x ...,21彼此相互独立,且是x 的无偏估计,所以:()()0ˆˆ=--j i x x xx E ()n j i j i ...2,1,,=≠ (2-25)则有:()∑∑==--=ni ni i i i w xx w 112222ˆσσ (2-26)上式中的σ是各加权因子i w 的多元二次函数,它的最小值的求取就是在加权因子n w w w ...,21满足归一化约束条件下多元函数极值的求取。



多证据判决信息融合基础信息融合的本质是系统的全面协调优化[5]:将不同来源、不同模式、不同媒质、不同时间、不同表示方法,特别是不同层次的信息加以有机地结合,寻求一种更为合理的准则来组合信息系统在时间和空间上的冗余和互补信息,以获得对被评估问题的一致性解释和全面的描述,从而使该系统获得比它的各个组成部分或其简单的加和更优越的性能。
现有的信息融合数学模型主要采用嵌入约束模型、证据组合模型和人工神经网络模型等。
证据理论的基本原理证据理论采用信度的“半可加性”原则,较好地对不确定性推理问题中主、客观性之间的矛盾进行了折衷处理。
而且,证据理论下先验概率的获得比主观Bayes方法要容易得多,已经成为构造具有更强的不确定性处理能力专家系统的一种有效手段。
以下给出证据理论的一些基本定义和定理首先定义框架信任测度似然测度定理2 (Dempster-Shafer证据合成公式)设m1和m2是Q上的两个mass函数,对于m(F)=0及在证据理论中,不同专家的经验和知识可以通过式(4)来有效融合;而某个诊断结论成立的可信度可以通过信任区间[Bel,Pl]来表示。
提高目标检测概率--多传感器信息融合已成为信息处理技术领域的研究热点问题近年来,随着基于多传感器系统的军事作战平台的形成和发展,多传感器信息融合已成为信息处理技术领域的研究热点问题。
对于多传感器的分布式检测,人们已经做了大量的研究。
而在双色红外成像系统中,如何充分利用双色红外传感器获得的图像信息来提高目标的检测概率,是实现远距离探测和抗干扰能力的关键。
其中,实现双色红外成像系统中远距离弱目标检测的一种有效途径,就是通过对目标在两个不同红外波段的成像信息进行融合处理。
这里所涉及到的图像信息融合,根据信息表征层次的不同,可以分为像素级融合、特征级融合和决策级融合。
像素级融合,是直接对各传感器图像的像素点灰度信息进行综合的过程。
特征级融合是对图像进行特征提取后,对各传感器图像的特征信息进行综合处理的过程。


Dempster-Shafer证据理论,也称为证据理论或D-S证据理论,是一种不精确推理理论,由A.P.Dempster 于1967年首先提出,而后他的学生G.Shafer在其研究的基础上加以完善和发展,形成了现在的证据理论。
该理论主要用于处理不确定信息的推理和决策问题,尤其在专家系统、人工智能、决策分析等领域中得到了广泛应用。
D-S证据理论的主要特点是满足比贝叶斯概率论更弱的条件,并具有直接表达“不确定”和“不知道”的能力。
它通过引入基本概率分配函数(basic probability assignment, bpa)来描述证据对某个假设的影响程度,从而将不确定信息量化为概率值。
此外,D-S证据理论还通过组合不同来源的证据来解决不确定性问题,通过Dempster合成规则将不同证据源的信息综合起来,得到更准确的推理结果。
尽管D-S证据理论在不确定信息处理方面具有许多优点,但也存在一些局限性。
例如,证据必须是独立的,而这在实际问题中往往难以满足;Dempster合成规则没有坚实的理论基础,其合理性和有效性也存在争议;在计算上可能存在指数爆炸的问题。
总之,Dempster-Shafer证据理论是一种处理不确定信息的有效方法,在许多领域中得到了广泛应用。
然而,其也存在一些局限性和需要进一步研究的问题。

ds证据理论
ds证据理论是一种证明方法,它旨在建立一个有效的、可靠的、有效的评估过程,以便根据可用的证据来确定事实。
它是一种基于统计学和科学原理的形式化理论,用于收集、评估、储存和分析信息,以便识别和检验事实,并为做出正确决策提供指导。
DS证据理论的元素包括:数据、技术、过程、数据库和工具,以及多种可用于收集、储存和分析信息的技术。
它包括:采用合理的技术,以有效的方式收集和存储数据;从数据中提取适当的细节;使用合理的工具和技术来分析数据,以帮助支持或证明某一论点;使用合理的技术来识别不可靠的数据;将所有结果总结起来,以便更好地识别事实。
《基于DS证据理论的多传感器数据融合算法研究与应用》篇一一、引言随着传感器技术的快速发展,多传感器数据融合技术已成为现代信息处理领域的重要研究方向。
多传感器数据融合技术能够有效地整合来自不同传感器的信息,提高系统的准确性和可靠性。
DS(Dempster-Shafer)证据理论作为一种重要的信息融合方法,为多传感器数据融合提供了有效的理论支持。
本文将基于DS证据理论,对多传感器数据融合算法进行研究,并探讨其在实际应用中的效果。
二、DS证据理论概述DS证据理论是一种利用多个证据来推理出假设的方法。
该理论具有将各种证据组合在一起并推导出共同结论的优点。
DS证据理论的主要原理是通过对不同的数据信息进行赋值,并根据一定的组合规则来得到每个假设的信任度,进而得出最终结论。
该理论在多传感器数据融合中具有广泛的应用前景。
三、多传感器数据融合算法研究(一)算法原理基于DS证据理论的多传感器数据融合算法主要包括以下几个步骤:首先,从不同的传感器中获取数据信息;其次,根据DS证据理论对每个传感器数据进行赋值;然后,根据一定的组合规则计算每个假设的信任度;最后,得出结论。
(二)算法实现在实现过程中,需要选择合适的传感器,并确保传感器之间的数据传输和同步。
同时,还需要对数据进行预处理和噪声消除等操作。
此外,为了满足实时性要求,还需要对算法进行优化和加速处理。
(三)算法优势基于DS证据理论的多传感器数据融合算法具有以下优势:首先,能够有效地整合来自不同传感器的信息,提高系统的准确性和可靠性;其次,能够处理具有不确定性和模糊性的信息;最后,能够适应不同的环境和场景需求。
四、应用实例分析(一)应用场景基于DS证据理论的多传感器数据融合算法在许多领域都有广泛的应用,如智能交通、智能安防、无人驾驶等。
以智能交通为例,该算法可以用于车辆检测、交通流量统计、交通事件识别等方面。
(二)应用效果以某城市交通监控系统为例,采用基于DS证据理论的多传感器数据融合算法后,能够有效地提高交通监控的准确性和实时性。
DS证据理论分析
证据权重表示一项证据对概率假设的支持程度,通常用一个介于0和1之间的数值表示。
当证据权重为1时,表示证据对概率假设的支持非常强,而当权重为0时,表示证据对概率假设没有任何支持。
信任函数则表示不同证据之间的组合方式,它是将证据权重映射到概率分配上的函数,通常采用的是Dempster-Shafer(DS)证据理论的规则。
DS证据理论的应用范围非常广泛,涵盖了多个领域。
例如,在法律领域,DS证据理论可以用于判断被告是否有罪,通过对不同证据的分析和组合,可以推断被告有罪的概率。
在医学诊断中,DS证据理论可以用于评估患者是否患有其中一种疾病,通过对患者的不同症状和检测结果的分析和组合,可以推断患者患病的可能性。
DS证据理论的分析过程可以分为三个主要步骤:观察证据、计算证据权重和组合证据。
观察证据是指从现实生活中收集和获取各种证据。
计算证据权重是指通过数学公式或计算方法,将证据的权重从原始数据转化为DS证据权重。
组合证据是指将不同证据的权重进行组合,得出最终的概率假设。
总结来说,DS证据理论是一种通过考虑证据权重和信任函数来推断概率假设真实度的方法。
该理论的应用广泛,可以用于法律、医学等多个领域。
在应用该理论进行分析时,需要考虑证据的可靠性和不确定性,以及对证据的观察、计算权重和组合证据三个主要步骤的操作。
ds证据理论
DS证据理论是一种用于数据挖掘和机器学习应用的理论。
它建立在统计概率理论和数学统计学的基础上,用于从大量数据中发现隐藏的规律和特征。
它的概念很简单,即从大量的数据中提取出有用的信息,并基于这些信息建立有用的模型。
DS证据理论的思想是,通过分析大量数据,发现不同的见解,有助于更好地了解和预测特定问题。
例如,可以使用DS证据理论来发现哪些消费者更有可能购买某一产品,以及产品的价格等等。
此外,它还可以用于发现病毒传播的规律、分析股市走势、计算机安全以及政策分析等方面。
DS证据理论的基本思想是使用统计概率理论和数学统计学来构建模型,并应用到大量数据中。
它的目标是从数据中推断出模型,并用来改善预测精度和提高预测精度。
DS证据理论的优势在于它可以从大量的数据中发现隐含的规律,为实际问题提供更准确的解决方案。
总之,DS证据理论是一种用于发现数据隐含规律的理论,它的优势在于可以提供准确的解决方案,为实际问题提供更准确的解决方案。
DS证据理论的应用已经广泛渗透到数据挖掘、机器学习、病毒传播、股市走势、计算机安全和政策分析等领域。
DS证据理论_学习笔记D-S证据理论_学习笔记注意,笔者⽔平⼀般,主要内容来源于参考资料,如有错误请多多指教。
不定期更新。
由来D-S证据理论全称“Dempster-Shafer证据理论”,源于美国哈佛⼤学数学家A. P. Dempster在利⽤上、下限概率来解决多值映射问题⽅⾯的研究⼯作。
后来他的学⽣G. Shafer引⼊信任函数的概念,形成了⼀套基于“证据”和“组合”来处理不确定性推理问题的数学⽅法。
1976年出版的《证据的数学理论》(A Mathematical Theory of Evidence)标志着证据理论正式成为了⼀种处理不确定性问题的完整理论。
证据理论的核⼼是Dempster在研究统计问题提出的、随后被Shafer推⼴的Dempster合成规则。
证据理论的优点是:1. 在证据理论中需要的的先验数据容易获得。
2. Dempster合成公式可以综合不同专家或数据源的知识或数据,⽤途⼴泛。
证据理论的缺点是:1. 要求证据必须是独⽴的,有时这不易满⾜。
2. 证据合成规则没有⾮常坚固的理论⽀持,其合理性和有效性还存在较⼤的争议。
3. 计算上存在着潜在的指数爆炸问题。
质疑证据合成规则合理性的问题之⼀:“Zadeh悖论”,详见参考资料。
为此有很多完善D-S证据理论的⼯作,感兴趣的请⾃⾏查找相关资料。
基本概念和推理过程⼊门理解D-S证据理论可以看这篇⽂章,对照着参考资料看就能有个⼤概的理解了。
这⾥仅仅是摘录基本概念和合成规则,以及个⼈理解,详细过程不再赘述。
基本概念基本概念有4基本概率分配英⽂全称:Basic Probability Assignment,简称BPA。
在假设空间上,使⽤⼀个叫做mass函数的函数率。
明显,对于同⼀个mass函数⽽⾔,假设空间中每个元素的概率之和等于1。
也即满⾜:(Focal elements)。
我感觉,⼀般不同的专家或者证⼈就会有不同的看法,也即有不同函数信任函数Belief function BPA m的信任函数定义为:似然函数Plausibility function BPA m的似然函数定义为:信任区间信任区间⽤于表⽰对某个假设的确认程度,⽐如假设A我简单理解为A的嫌疑⾄少是其⼦集的概率之和,⾄多是其涉及集合的概率之和。
一.D-S证据理论引入
诞生
D-S证据理论的诞生:起源于20世纪60年代的哈佛大学数学家A.P. Dempster利用上、下限概率解决多值映射问题,1967年起连续发表一系列论文,标志着证据理论的正式诞生。
形成
dempster的学生G.shafer对证据理论做了进一步发展,引入信任函数概念,形成了一套“证据”和“组合”来处理不确定性推理的数学方法
D-S理论是对贝叶斯推理方法推广,主要是利用概率论中贝叶斯条件概率来进行的,需要知道先验概率。
而D-S证据理论不需要知道先验概率,能够很好地表示“不确定”,被广泛用来处理不确定数据。
适用于:信息融合、专家系统、情报分析、法律案件分析、多属性决策分析
二.D-S证据理论的基本概念
定义1 基本概率分配(BPA)
设U为以识别框架,则函数m:2u→[0,1]满足下列条件:
(1)m(ϕ)=0
(2)∑A⊂U m(A)=1时
称m(A)=0为A的基本赋值,m(A)=0表示对A的信任程度
也称为mass函数。
定义2 信任函数(Belief Function)
Bel:2u→[0,1]
Bel(A)=∑B⊂A m(B)=1(∀A⊂U)
表示A的全部子集的基本概率分配函数之和
精品文库 2
定义3 似然函数(plausibility Function)
似然函数表示不否认A的信任度,是所有与A相交的子集的基本概率分配之和。
定义4 信任区间
[Bel(A),pl(A)]表示命题A的信任区间,Bel(A)表示信任函数为下限,pl(A)表示似真函数为上限
举例:如(0.25,0.85),表示A为真有0.25的信任度,A为假有0.15的信任度,A不确定度为0.6
三.D-S证据理论的组合规则
精品文库 3
m个mass函数的Dempster合成规则
其中K称为归一化因子,1−K即∑A1⋂...⋂A n=ϕm1(A1)⋅m2(A2)⋅⋅⋅m n(A n)反映了证据的冲突程度
精品文库 4
四.判决规则
设存在A1,A2⊂U ,满足
m(A1)=max{m(A i),A i⊂U}
m(A2)=max{m(A i),A i⊂U且A i≠A1}
若有:
m(A1)−m(A2)>ε1
m(Θ)<ε2
m(A1)>m(Θ)
则A1为判决结果,ε1,ε2为预先设定的门限,Θ为不确定集合
五.D-S证据理论存在的问题
精品文库 5
(一)无法解决证据冲突严重和完全冲突的情况
精品文库 6
该识别框架为{Peter,Paul,Mary},基本概率分配函数为m{Peter},m{Paul},m{Mary} 由D-S证据理论的基本概念和组合规则进行解析
精品文库7
精品文库8
精品文库9
精品文库10
可以看出虽然在W1,W2目击中,peter和mary都为0.99,但是存在严重的冲突,造成合成之后的Bel函数值为0,这显然与实际情况不合,更极端的情况如果W1中
m{peter)=1,W2中m{Mary}=1,则归一化因子K=0,D-S组合规则无法进行
精品文库11
精品文库12
精品文库13
精品文库14
精品文库15
精品文库16
精品文库17
精品文库18
(二)难以辨识模糊程度
由于证据理论中的证据模糊主要来自于各子集的模糊度。
根据信息论的观点,子集中元素的个数越多,子集的模糊度越大
精品文库19
精品文库20
(三)基本概率分配函数的微小变化会使组合结果产生急剧变化
精品文库21
精品文库22
精品文库23
在学习笔记(一)中,对D-S证据理论引入,对D-S证据理论的基本概念和存在的问题进行了学习。
学习笔记(二)对证据理论的改进方法进行学习,主要学习了Yager的合成公式
一.Yager合成公式
精品文库24
改进中主要引入了m(X),把冲突给了未知命题
精品文库25
精品文库26
精品文库27
精品文库28
精品文库29
二.Yager合成公式改进
为了解决多个证据中有一个证据否定A,则合成结果也否认A,对Yager公式进行改进
精品文库30
精品文库31
精品文库32
精品文库33
例2:
精品文库34
精品文库35
精品文库36。