下载文档原格式
第三节力的等效和替代一、共点力1．影响力的作用效果的因素有：力的大小、方向和作用点。
物理学中称之为力的三要素。
2．如果几个力都作用在物体的同一点上，或者几个力的作用线相交于同一点，这几个力就称为共点力。
二、力的等效和替代1．如果一个力的作用效果与另外几个力的共同作用效果相同，那么这个力与另外几个力等效或可以相互替代，这个力称为另外几个力的合力，另外几个力称为这个力的分力。
从作用效果相同这一观点出发，根据具体情况进行力的替代，称为力的合成与分解。
2．求几个力的合力的过程或方法，叫做力的合成。
求一个力的分力的过程或方法，叫做力的分解。
三、寻找等效力 利用力的形变效果相同寻找等效力，得出的合力与分力的关系是：合力可以用以两个分力为邻边所作平行四边形的两个邻边之间的对角线表示，即对角线表示合力的大小和方向。
1.力的三要素：力的大小、方向和作用点。
2．如果几个力都作用在物体的同一点上，或者几个力的作用线相交于同一点，这几个力就称为共点力。
3．从作用效果相同这一观点出发，根据具体情况进行力的替代，称为力的合成与分解。
1．自主思考——判一判(1)共点力一定作用于物体上的同一点。
(×)(2)共点力一定作用于同一物体上。
(√)(3)合力与分力同时作用在物体上。
(×)(4)合力就是物体实际受到的几个力的和。
(×)(5)合力的作用效果与分力共同作用的效果相同，它们等效。
(√)2．合作探究——议一议(1)一个成年人或两个孩子均能提起同一桶水，那么该成年人用的作用力与两个孩子用的力效果是否相同？二者是否可以等效替换？图3-3-1提示：相同，可以等效替换。
(2)合力大小一定大于分力大小吗？提示：不一定。
由平行四边形的边长和对角线长度可知，合力大小可以比分力大，可以比分力小，还可以与分力相等。
1．共点力的几种情况(1)几个力同时作用于同一点(即力的作用点重合)，如图3-3-2甲所示。
图3-3-2(2)同时作用在同一物体上的几个力，虽然作用点并不重合，但是这几个力的作用线的正向或反向延长线能够相交于同一点，如图乙所示。
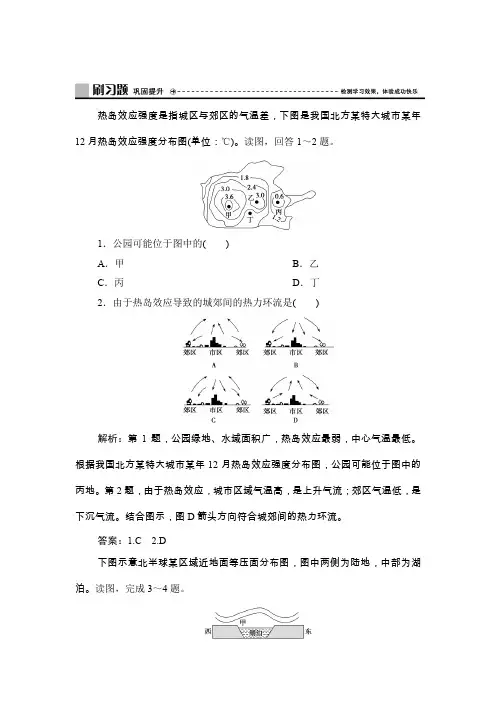
热岛效应强度是指城区与郊区的气温差，下图是我国北方某特大城市某年12月热岛效应强度分布图(单位：℃)。
读图，回答1～2题。
1．公园可能位于图中的()A．甲B．乙C．丙D．丁2．由于热岛效应导致的城郊间的热力环流是()解析：第1题，公园绿地、水域面积广，热岛效应最弱，中心气温最低。
根据我国北方某特大城市某年12月热岛效应强度分布图，公园可能位于图中的丙地。
第2题，由于热岛效应，城市区域气温高，是上升气流；郊区气温低，是下沉气流。
结合图示，图D箭头方向符合城郊间的热力环流。
答案：1.C 2.D下图示意北半球某区域近地面等压面分布图，图中两侧为陆地，中部为湖泊。
读图，完成3～4题。
3．此时()A．湖泊为低压B．陆地为高压C．可能为白天D．湖泊气温高4．此时甲处的风向可能为()A．东南风B．东北风C．西南风D．西北风解析：第3题，根据等压面凸凹与气压高低的关系，可判断出湖泊为高压，气温低；陆地为低压，气温高，风由湖泊吹向陆地，可能为白天。
第4题，由于湖泊为高压，陆地为低压，风由湖泊吹向陆地，近地面风向受地转偏向力及摩擦力的影响，甲处风向为东南风。
答案：3.C 4.A下图中箭头表示气流的运动方向，图中M点海拔为241米，N点海拔为480米。
读甲、乙两幅图，完成5～6题。
5．图中气流运动体现的地理现象是()A．海陆风B．焚风C．山谷风D．季风6．下列关于图中地理现象的描述，正确的是()A．甲图发生在白天，乙图发生在夜晚B．甲图发生在夜晚，乙图发生在白天C．甲图发生在冬季，乙图发生在夏季D．甲图发生在夏季，乙图发生在冬季解析：第5题，甲图中气流由山谷吹向山顶，乙图中气流由山顶吹向山谷，属于山谷风。
第6题，甲图为谷风，发生在白天；乙图为山风，发生在夜晚。
答案：5.C 6.A特朗勃墙是一种依靠墙体独特的构造设计，无机械动力、无传统能源消耗、仅依靠被动式收集太阳能为建筑供暖的集热墙体。
其冬季白天工作原理如下图。
据此回答7～8题。
第三章第三节让改革创新成为青春远航的动力
一、改革开放是当代中国的显著特征
改革开放是党在新的历史条件下领导人民进行新的伟大革命，是决定当代中国命运的关键抉择。
实践证明，改革开放是当代中国发展进步的活力之源
以数千年大历史观之，变革和开放总体上是中国的历史常态
商鞅变法王安石变法戊戌变法……
改革开放是当代中国最鲜明的特色
中国特色社会主义之所以具有蓬勃的生命力，就在于实行的是改革开放的社会主义创新是改革开放的生命
二、改革创新是新时代的迫切要求
创新决定未来，改革关乎国运。
创新是推动人类社会发展的第一动力
创新决定着世界政治经济力量对比的变化，也决定着各国各民族的前途命运。
创新能力是当今国际竞争新优势的集中体现
改革创新是赢得未来的必然要求
如何做？
必须把创新作为引领发展的第一动力，把人才作为支撑发展的第一资源，把创新
摆在国家发展全局的核心位置，把创新驱动发展战略作为国家重大战略，让创新
贯穿党和国家一切工作，让创新在全社会蔚然成风。
实施创新驱动发展战略，最根本的是要增强自主创新能力，最紧迫的是要破除体
制机制障碍，让改革释放创新活力，让一切创新源泉充分涌流。
三、做改革创新生力军
青年人如何做改革创新的实践者？
（一）树立改革创新的自觉意识
增强改革创新的责任感
树立敢于突破陈规的意识
树立大胆探索未知领域的信心
（二）增强改革创新的能力本领
夯实创新基础
培养创新思维
投身改革创新实践。
第三章第三节药物消除动力学从生理学看，体液被分为血浆、细胞间液及细胞内液几个部分。
为了说明药动学基本概念及规律现假定机体为一个整体，体液存在于单一空间，药物分布瞬时达到平衡（一室模型）。
问题虽然被简单化，但所得理论公式不失为临床应用提供了基本规律。
按此假设条件，药物在体内随时间变化可用下列基本通式表达：dC/dt=kCn.C为血药浓度，常用血浆药物浓度。
k 为常数，t为时间。
由于C为单位血浆容积中的药量（A），故C也可用A代替：dA/dt=kCn，式中n=0时为零级动力学（zero-order kinetics），n=1时为一级动力学（first-order kinetics），药物吸收时C（或A）为正值，消除时C（或A）为负值。
在临床应用中药物消除动力学公式比较常用，故以此为例如以推导和说明。
一、零级消除动力学当n=0时，-dC/dt=KC0=K（为了和一级动力学中消除速率常数区别，用K代k），将上式积分得：Ct=C0- Kt，C0为初始血药浓度，Ct为t时的血药浓度，以C为纵座标、t为横座标作图呈直线（图3-6），斜率为K，当Ct/C0=1/2时，即体内血浆浓度下降一半（或体内药量减少一半）时，t为药物消除半衰期（half-life time， t1/2）。
按公式1/2C0=C0-Kt1/2可见按零级动力学消除的药物血浆半衰期随C0下降而缩短，不是固定数值。
零级动力学公式与酶学中的Michaelis-Menten公式相似：，式中S为酶的底物，Vmax为催化速度，Km 为米氏常数。
当[S]>>Km时，Km可略去不计，ds/dt=Vmax，即酶以其速度催化。
零级动力学公式与此一致，说明当体内药物过多时，机体只能以能力将体内药物消除。
消除速度与C0高低无关，因此是恒速消除。
例如饮酒过量时，一般常人只能以每小时10ml乙醇恒速消除。
当血药浓度下降至消除能力以下时，则按一级动力学消除。
二、一级消除动力学当n=1时，-dC/dt=keC1=keC，式中k用ke表示消除速率常数（elimination rate constant）。
第三章第三节
1。
什么叫元组关系演算？
答案1在元组演算中，元组关系演算表达式（简称元组表达式）的一般形式为|t|P(t)其中，t是元组变量，表示一个元数默写固定的元组；P是公式（即计算机语言中条件表达式）。
{t|P（t）}表示满足公式P的所有元组t的集合。
答案2
关系演算分为元组关系演算或域关系演算，前者以元组为变量，后者以域为变量。
元组演算表达式的一般形式为：{t|P(t)}，其含义为：这是一个元组集合，其中的每个元组t(t是元组变量)满足公式P所规定的条件。
2。
元组演算的公式定义法则中，规定的原子公式有那三种形式？
（1）R（s）。
其中，R是关系名，s是元组变量。
（2）s[i]Øu[j]。
其中，s和u元组变数，Ø是算术比较运算符,s[i]和u[j]分别表示是s 第i个分量和u的第j个分量。
（3）s[i]Øa或aØ u[j]。
这是a是常量。
3。
元组演算的公式定义法则中，规定的三种形式的原子公式各表示何种命题？
（1）R（s）。
其中，R是关系名，s是元组变量。
它表示这样一个命题：“s是关系R的一个元组”
（2）s[i]Øu[j]。
其中，s和u元组变数，Ø是算术比较运算符,s[i]和u[j]分别表示是s 第i个分量和u的第j个分量。
s[i]Øu[j]这样命题：“元组s的第i个分量与元组u的j个分量之间满足Ø关系。
”
（3）s[i]Øa或aØ u[j]。
这是a是常量。
前一个原子公式s[i]Øa表示命题:“元组s的i 个分量值与常量a之间满足Ø关系”。
4。
试述元组演算公式中各运算符优先次序？
优先次序如下：括号、算术比较运算符、
¬∧∨
5、设有R、S两个关系给出与五种基本关系代数运算相应的原组元算表达式。
(1)RUS可用{t|R(t)∨S(t)}表示
(2)R—S可用{t|R(t)∧¬S(t)}表示
(3)R×S可用{t|(∃u)(∃v)(R(u) ∧ S(v)∧t[1]=u [1]∧ t[2]=u[2] ∧ t[3]=u[3] ∧ t[4]=v[1] ∧ t[5]=v[2])
∧[2] ∧t[6]=v[3]}表示
(4)设投影操作是∏2,3(R),那么元组表达式写成:
{t|(∃u)(Ru) ∧t[1] ∧=u[2] ∧t[2]=u[3]}
(5)бf(R)可用|t|R}表示，F’是F的等价表示形式。
如б2=’d’可写成{t|R(t)∧t[2]=’d’}。
用
6。
证明合并运算的元组元算表达式与相应关系代数表达式的等价性。
设有两个关系R和S具有相同的关系模式，R与S的并是属于S的元组构成的集合，记为R∪S。
形式定义如下：
R∪S≡{t|{t|t∈R∨t∈S},t是元组变量，R和S的元数相同
7。
证明求差运算的元组元算表达式与相应关系代数表达式的等价性。
关系R和S具有相同的关系模式，R的差是由属于R但不属于S的元组构成的集合，记为R-S。
形式定义如下：
R-S≡{t|{t∈R∧t-∈S},R和S元数相同。
8.元组演算的公式定义法则中规定的原子公式有那几种？说明每一种原子公式所表达的命题？
1．R(x).r是h中的关系，x是元组变量，r（x）表示x∈r：
2．X[A] ØC或者CØx[B]。
x为元组变量，A、B为U中的属性，C为A或B对应的域中的常量，Ø为比较运算符，x[A] ØC表示x的A分量与C之间有Ø关系：CØx[B]类似。
3．x[A] Øy[B]。
x、y为元组变量，A、B为U中的属性，Ø为比较运算符号。
x[A] Øy[B]表示x的A分量与y的B分量之间的有Ø关系。
