无刻度直尺作图

无刻度直尺作图教学目标：学会用无刻度直尺完成作图，并体会作图过程中包含的数学思想。

教学手段：学讲方式教学用具：PPT课型：微课教学过程：情景引入：作图是考查我们数学思想和数学能力的重要手段，尺规作图时利用全等这一基本原理完成的。

只用直尺(无刻度) 作图，具有趣味性、探索性、创造性，它注重数学思维的考查．由于少了圆规的相助，直尺只能用来画直线、射线或线段，以及由它们组合成的图形．解答此类问题时，在动手操作探索作图思路的过程中，我们会感受到数学创造的乐趣．今天我们就以画中点为例来探索用无刻度直尺作图的基本方法和思路。

展示例题：已知矩形ABCD，请你只用无刻度的直尺画出BC边的中点．讨论分析：看到此题，会让人感到无从下手，因为无刻度直尺只能用来画线段、射线、直线，以及由它们组合而成的图形，而且为了得到确定的线，只能连接确定的点。

因此就要认真分析已知条件，矩形对边平行。

由平行可联想到中位线、平行线截得的线段对应成比例。

虽然中位线与中点关系密切，但至少需要一个中点，因此于解题关系不大。

而平行线截得的线段对A C BD OE FGH应成比例可以用来解决此问题。

画法展示：首先在AD 上方任取一点Q ，连接OB,OC,分别交AD 于E 、F,确定的点出现。

再连接BF 、CE 交于点G ，又一个新的确定的点出现。

最后连接OG 并延长交BC 于点H ，则点H 就是BC 边的中点。

证明过程： 证明：∵四边形ABCD 是矩形 ∴AD//BC∴HCEMGC EG GC EG BC EF BC EF OB OE OB OE BH EM ====,,∴HC EMBH EM= ∴BH=HC 即点H 为BC 的中点。

小结：无刻度直尺除了能作中点外，还可以作三角形的高，画轴对称，画角平分线。

课后练习：知AB 是半圆的直径，图1中，点C 在半圆外，图2中，点C 在半圆内，请仅用无刻度的直尺，(1) 在图1中，画出△ABC 的三条高的交点：(2) 在图2中，画出△ABC 中AB 边上的高．。

仅用无刻度直尺作图1.如图，在平行四边形ABCD中，点E在BC上，且AE=EC，请仅用无刻度直尺按下列要求作图（保留作图痕迹）.（1）在图1中，作出∠DAE的平分线；（2）在图2中，作出∠AEC的平分线；图1 图22.如图，在菱形ABCD中，∠B=60°，E是AB边的中点，请仅用无刻度直尺按下列要求作图（保留作图痕迹）.（1）过点E作边AB的平行线；（2）作出边AB的垂直平分线.图1 图23.如图，在平形四边形ABCD中，AE是∠BAD的平分线.请仅用无刻度直尺按下列要求作图（保留作图痕迹）.（1）在图1中，以AD为腰作一个等腰三角形；（2）在图2中，以AE为边作平行四边形AECF.图1 图24.如图，△ABC内接于⊙O，∠B=45°．请仅用无刻度的直尺按下列要求作图（保留作图痕迹）．（1）在图1中，以AC为边作一个圆内接正方形；（2）在图2中，AB=CB，CD为⊙O的切线，过点A作⊙O的切线AE．图1 图25.如图，点E是正方形ABCD内一点，EB=EC，且∠E≠90°．请仅用无刻度的直尺按要求作图（保留画图痕迹，不写作法）．（1）在图1中，作出BC边的中点F．（2）在图2中，作出CD边的中点G．图1 图26.如图，在平面直角坐标系中，点A，B，C，D的坐标分别为（1，0），（3，0），（3，1），（1，1）．请仅用无刻度的直尺，分别在图1、图2中画出满足条件的直线（保留画图痕迹）．（1）在图1中，画直线m：y=-x+1；（2）在图2中，画直线n：y=x-1．图1 图27.如图，在等腰△ABC和▱BECD中，AB=AC，DB⊥BC，请仅用无刻度直尺完成以下作图．（保留作图痕迹）（1）在图1中，作出△ABC的边BC上的高AM．（2）在图2中，作出△BCD的边BD上的中线CN．图1 图28.如图是由7×6个小正方形组成的网格图，已知A，B为格点．请仅用无刻度直尺根据下列要求作图.（保留作图痕迹）（1）在图1中，作线段AB的垂直平分线；（2）在图2中，作∠AOB的平分线．图1 图29.如图是由小正方形组成的6×6网格，每个小正方形的顶点叫做格点．△ABC的三个顶点都是格点，仅用无刻度的直尺在给定的网格中完成作图．（保留作图痕迹）（1）在图1中，作AC边上的高线BD；（2）在图2中，在BC上找出一点G，使得∠BAG=45°.图1 图210.如图是由小正方形构成的6×6网格，每个小正方形的顶点叫做格点．⊙P 经过格点A ，B ，C ，请仅用无刻度直尺根据下列要求作图.（保留作图痕迹） （1）在图1中，⊙P 确定的圆心P ； （2）在图2中，作弦BD ，使BD 平分∠ABC .图1 图211. 已知在 Rt△ABC 中， AB=AC ， ∠BAC=90° ， AD⊥BC ，点 E ， F 分别是 AB ， AD 的中点，请仅用无刻度直尺完成以下作图（保留作图痕迹）.12.如图，已知等腰Rt △ABC和等腰Rt △DEF ,∠ABC =90∘ ,∠DEF =90∘，点F，E，B，C在同一条直线上，连接AF.请在图①、图②中仅用无刻度的直尺画出△ACF中AF边上的高CM（保留作图痕迹） （1） 如图①，作△ACD的中线DM；（2） 如图①，作正方形ADCP.（1） 如图①，点B与点E重合；（2） 如图①，点E在CB的延长线上.参考答案仅用无刻度直尺作图1.解：（1）如解图1，AC即为所求；（2）如图2，EF即为所求.解图1 解图22.解：（1）如解图1，直线EF即为所求；（2）如解图2，直线DG即为所求.解图1 解图23.解：（1）如解图1，△ADG即为所求；（2）如解图2，平行四边形AECF即为所求.解图1 解图2 4.解：（1）如解图1，正方形AFGC即为所求；（2）如解图2，AE即为所求.解图1 解图25.解：（1）如解图1，点F即为所求；（2）如解图2，点G即为所求.解图1 解图26.解：（1）如解图1，直线m即为所求；（2）如解图2，直线n即为所求.解图1 解图27.解：（1）如解图1，AM即为所求；（2）如解图2，CN即为所求．解图1 解图28.解：（1）如图，直线CD即为所求；（2）如图，射线OP即为所求．解图1 解图29.解：（1）如解图1，BD即为所求；（2）如解图2，点G即为所求．解图1 解图210.解：（1）如解图1，点P即为所求；（2）如解图2，BD即为所求．解图1 解图211.（2）12.（1）（2）。

数学(江西)
第2部分 专题突破
解：(1)如图11，直线l即为所求； (2)如图12，点M即为所求．
图11
图12
数学(江西)
第2部分 专题突破
3．如图，将矩形纸片ABCD沿对角线BD折叠，点 C落在点C′处，BC′与AD相交于点O，请你仅用无刻度 的直尺，用两种不同的方法分别在图1、图2中作出 ∠BOD的平分线OP.
数学(江西)
第2部分 专题突破
训练 10.请仅用无刻度的直尺按照下列要求作 图．
(1)在图1所示的正方形网格中作出以AB为对角线 的正方形；
(2)在图2所示的菱形网格中作出线段CD的三等分 点．
图1
图2
数学(江西)
第2部分 专题突破
解：(1)如图27，正方形AEBF即为所求； (2)如图28，点M，N即为所求．
第2部分 专题突破
解：(1)如图9，CQ即为所求； (2)如图10，AF即为所求．
图9
图10
数学(江西)
第2部分 专题突破
2．已知矩形
ABCD，请仅用无刻
度的直尺按下列要
求作图．(不写作法)
(1) 如 图 1 ， 点 P
为 CD 的 中 点 ， 画 出
AB的垂直平分线l；
图1
图2
(2)如图2，在矩形ABCD中，以对角线AC为一边构 造一个正方形ACFE，画出EF的中点M.
图30
数学(江西)
第2部分 专题突破
12．如图，图1、图2均是4×4的正方形网格，每 个小正方形的顶点称为格点，四边形ABCD的顶点均在 格点上，仅用无刻度直尺，分别按下列要求画图，保 留作图痕迹．
数学(江西)
第2部分 专题突破
(1)在图1中的线段CD上找到一点E，连接AE，使

5
在菱形ABCD中，点E为AB的中点。 （1）如图1，在CD上找点F，使点F是CD的中点； （2）如图2，在AD上找点G，使点G是AD的中点。
6
（1）图1是矩形ABCD，E，F分别是AB和AD的中点， 以EF为边画一个菱形； （2）图2是正方形ABCD，E是对角线BD上任意一点 （BE>DE），以AE为边画一个菱形。
12
□ABCD中，点E在AD上，DE=CD。 （1）在图1中，画出∠C的角平分线； （2）在图2中，画出∠A的角平分线。
13
在正方形ABCDபைடு நூலகம்，M是BC边上任意一点。 （1）在图1中AB边上找一点N，使CN=AM； （2）在图2中AD边上找一点Q，使CQ∥AM。
14
在如图所示的2×4正方形网格中， △ABC为格点三 角形。 （1）sin∠ACB=＿； （2）用无刻度的直尺在网格中画出与△ABC成轴对 称的格点三角形（画出两种即可）。
10
（1）如图1，在△ABC中，AB=AC，M、N分 别是边AB、AC上的两点，且BM=CN，请画出 线段BC的垂直平分线； （2）如图2，在菱形ABCD中，∠B =60 °，E 是AB边的中点，请画出线段BC的垂直平分线。
11
在10×10的正方形网格中（每个小正方形的边长为 1），线段AB在网格中人位置如图所示。 （1）在图1中，画出一个以AB为边，另两个顶点C、D 也在格点上的菱形ABCD； （2）在图2中，画出一个以A、B为顶点，另两个顶点 C、D也在格点上的菱形，且使这个菱形的面积最大或 最小（仅选其一，即可）；其面积是＿。
图1
图2
20
线段AB是⊙O的直径，BC⊥CD,AD ⊥CD. （1）图1中，当线段CD与圆相切时，请在CD上确定一点E，

3.如图矩形ABCD中，点E在BC上，且AE=EC，试分别在下列 两个图中按要求使用无刻度的直尺画图。
（1）在图1中，画出∠DAE的平分线； （2）在图2中，画出∠AEC的平分线．
规律总结
第一步：找出图形的对称中心（对称轴） 第二步：根据平行四边形的性质，分析要找的点与 哪个已知点关于对称中心对称，并根据对称中心作 出对称点 第三步：连线，作出题目要求的图形，并进行说明
无刻度直尺作图 —— 平行四边形篇
教学目标
1.经历探索与实践的过程，会结合平行四边形的性质，用无刻 度直尺作出已知点的对称点以及中心对称图形。
2.通过作图，培养学生的动手操作能力、逻辑思维能力、分析 和解决问题的能力.
回顾
什么是无刻度直尺作图？ 利用无刻度直尺作出几何图形。 无刻度直尺的功能：作任意直线、连任意两点、延长任意线段
（2）如图2，在菱形ABCD中，∠B =60 °，E是AB边的中 点，请画出线段BC的垂直平分线。
挑战自我
已知正方形ABCD如图所示，M，N在直线BC上，MB=NC。 试分别在图1、图2中画出一个不同的等腰三角形OMN。
小结
1、在以平行四边形为问题背景的无刻度直尺作图一般步骤？
第一步：找出图形的对称中心（对称轴） 第二步：根据平行四边形的性质，分析要找的点与哪个已知点关于对称 中心对称，并根据对称中心作出对称点 第三步：连线，作出题目要求的图形，并进行说明
2、无刻度直尺作图在平行四边形中意义？
巩固了对平行四边形的认识，并对平行四边形的对称性有了进一 步的了解，通过动手操作对图形的变换有了更深的理解。
3、无刻度直尺作图还可以在哪些情况下进行？
网格、圆、正多边形等
谢谢！再见！
小试牛刀

二 、用 无刻 度直 尺 同时 平分 平行 四边 形和 圆 的面 积
例 ２ 如 图２，己知 ：ＱＯ位 于 平 行 四边
形 ＡＢＣＤ 内 ，用无 刻 度 直 尺 将 ＱＯ和 平 行
四边形 ＡＢＣＤ 的面 积 同时 平分 ．
【作法 】
１．连 结对 角 Ｃ、ＢＤ，其交 点 为０ ；
Ｂ
２．过 ０和 ０ 用无 刻度 直尺 作 直线 Ｚ交
·
．
．
／４ ＣＢ ： ／＿＿ＡＤＢ：９０”，￣［ＩＡＤ上ＰＢ，ＢＣ３ＰＡ． ＿
· 点 为 △ＡＰＢ的垂 心．
．
．
‘
．
．
ＰＨ ＬＡＢ．
从 以上 几例 可 以看 出，用无 刻度直尺作一类特殊 要求 的几
何 图形 ，就是根据 己给命题 内含的特 殊性 ，再根据 几何公理 ，即
经过两 点有且只有一条直线 而作出的 ，这就 需要 我们对 问题有
．．
又·．·ｏ０．既是 轴对 称 图形 又是 中心对 称 图形 ，而直 线 Ｚ又过 圆 心 ０，
· 直 线 Ｚ平 分 ｏ０ 的面 积．
．
．
故 直线 Ｚ同时平分 ｏ０和平 行 四边 形 ＡＢＣＤ 的面 积．
三 、用 无刻 度直 尺作 已知 直 线的 垂线
例３ 如 图３，己知 ：点Ｊｐ为半 ｏＤ外 的一 点 ，用无刻 度 直尺 过 点Ｐ作ＡＢ
一 、 用 无刻 度直 尺将 三 角形 面积 三等 分 例 １ 如 图 １，己知 ：点 Ｇ为 ＡＡＢＣ的重 心 ，用 无 刻 度 直 尺 将 其 面 积 三 等 分． 【作法 】分别过Ａ、Ｇ；Ｂ、Ｇ；Ｃ、Ｇ用无刻度直尺作直线 ｚ 、ｚ 、ｚ 交 ＢＣ、 、 于 Ｄ、 、Ｆ，则Ｚ 、ｆ１、Ｚ 将 △ＡＢＣ的面 积三 等 分． 证 明 ：设 ＡＢＧＣ和 ＡＡＢＣ的高为ｈ 、ｈ， 在 ＡＢＧＣ和 ＡＡＢＣ中 ，

1．用无刻度的直尺作图，保留作图痕迹．（1）在图1中，BD是△ABC的角平分线，作△ABC的平分内角C的角平分线；（2）在图2中，AD是∠BAC的角平分线，作△ABC的∠BCA相邻的外角的角平分线．2．如图，在菱形ABCD中，P是BC的中点，请用无刻度的直尺按要求画图．（1）在图①中画出AD的中点；（2）在图②中的对角线AC上取两个点E、F，使AE=CF．3．如图，以AB为直径的⊙O交△ABC的BC、AC边与D、E两点，在图中仅以没有刻度的直尺画出三角形的三条高（简单叙述你的画法）．4．如图，在▱ABCD中，E，F分别在边AD，BC上，且AE=CF，连接EF，请你只用无刻度的直尺画出线段EF的中点O，并说明这样画的理由．5．如图，四边形ABCD是平行四边形，点E在AD上，请仅用无刻度直尺按要求作图（保留作图痕迹，不写作法）（1）在图1中，过点E作直线EF将四边形ABCD的面积平分；（2）在图2中，DE=DC，作∠A的平分线AM；6．如图，⊙O是△ABC的外接圆，AB=AC，P是⊙O上一点．（1）操作：请你只用无刻度的直尺，分别画出图①和图②中∠P的平分线；（2）说理：结合图②，说明你这样画的理由．7．如图，AE为菱形ABCD的高，请仅用无刻度的直尺按要求画图．（不写画法，保留作图痕迹）．（1）在图1中，过点C画出AB边上的高；（2）在图2中，过点C画出AD边上的高．8．如图，已知在边长相等的小正方形组成的网格中，点A，B，C均在格点上，连接BC．（1）求tan∠ABC的值；（2）在网格中，用无刻度直尺，画出∠CBD，使tan∠CBD=．9．如图，在正六边形ABCDEF中，连接BD，请用无刻度的直尺，完成下列作图（1）如图①，作出一个边长等于BD的等边三角形；（2）如图②，作出一个周长等于BD的等边三角形．。

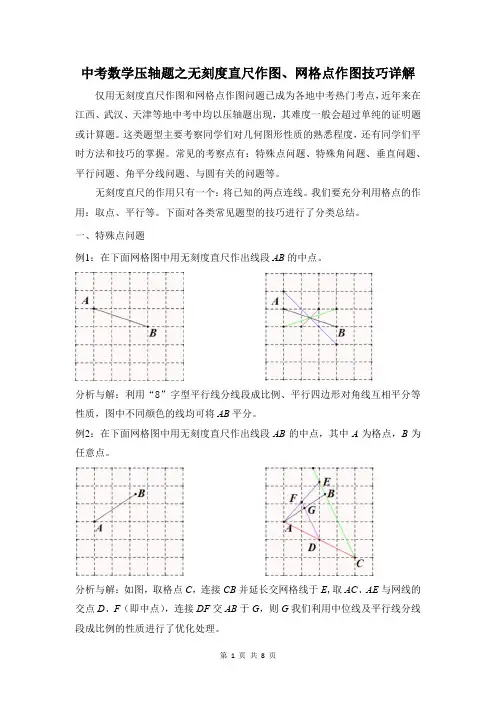
中考数学压轴题之无刻度直尺作图、网格点作图技巧详解仅用无刻度直尺作图和网格点作图问题已成为各地中考热门考点，近年来在江西、武汉、天津等地中考中均以压轴题出现，其难度一般会超过单纯的证明题或计算题。

这类题型主要考察同学们对几何图形性质的熟悉程度，还有同学们平时方法和技巧的掌握。

常见的考察点有：特殊点问题、特殊角问题、垂直问题、平行问题、角平分线问题、与圆有关的问题等。

无刻度直尺的作用只有一个：将已知的两点连线。

我们要充分利用格点的作用：取点、平行等。

下面对各类常见题型的技巧进行了分类总结。

一、特殊点问题例1：在下面网格图中用无刻度直尺作出线段AB的中点。

分析与解：利用“8”字型平行线分线段成比例、平行四边形对角线互相平分等性质，图中不同颜色的线均可将AB平分。

例2：在下面网格图中用无刻度直尺作出线段AB的中点，其中A为格点，B为任意点。

分析与解：如图，取格点C，连接CB并延长交网格线于E,取AC、AE与网线的交点D、F（即中点），连接DF交AB于G，则G我们利用中位线及平行线分线段成比例的性质进行了优化处理。

例3：在下面网格图中，在线段AB 上找一点C ，使AB AC 31=。

方法1方法2 方法3分析与解：方法1和方法2都利用了网格线平行的性质，通过“8”字型模型，构造1：2的相似比例，从而将线段AB 分为1：2两段。

方法3利用了重心的性质，AB 和EF 为BED ∆的两条中线，所以C 为BED ∆的重心。

二、特殊角问题例4：在下面网格图中找格点C ，使O BAC 45=∠。

分析与解：利用“12345”模型，即若βα、均为锐角，且31tan ,21tan ==βα，则O 45=+βα。

例5：如下图，利用无刻度直尺在线段MN 上找一点Q ，使O AQB 45=∠。

分析与解：O AQB 45=∠，典型定弦定角问题。

注意到O AMB 90=∠，所以点Q 在以M 为圆心，MA 长为半径的圆上，故2=MQ 。

实用文档
1、已知正方形ABCD如图所示，M、N在直线BC上，MB=NC，试分别在图1、图2中仅用无刻度的直尺画出一个不同的等腰三角形OMN．
2、如图，△ABC和△DCE都是等边三角形，且点C是线段AD的中点，请仅用无刻度直尺完成以下作图：（1）作BC的中点P；（2）过点C作AD的垂线．
3、请按要求，只用无刻度的直尺作图（请保留画图痕迹，不写作法）如图，已知∠AOB，OA=OB，点E 在OB边上，四边形AEBF是平行四边形，在图中画出∠AOB的平分线．
4、▱ABCD中，点E在AD上，DE=CD，请仅用无刻度的直尺，按要求作图（保留作图痕迹，不写作法）（1）在图1中，画出∠C的角平分线；（2）在图2中，画出∠A的角平分线．
5、如图，在△ABC中，AB=AC，M、N分别是边AB、AC上的两点，且BM=CN，请仅用无刻度的直尺画出线段BC的垂直平分线；
6、如图▱ABCD中，点E在BC上，且AE=EC，试分别在下列两个图中按要求使用无刻度的直尺画图（保留作图痕迹）．
（1）在图1中，画出∠DAE的平分线；（2）在图2中，画出∠AEC的平分线．
7、如图，在▱ABCD中，AC为对角线，AC=BC，AE是△ABC的中线．
（1）在图1中用无刻度的直尺画出△ABC的高CH；
（2）在图2中用无刻度的直尺画出△ADC的高AK。

无刻度直尺网格作图的基本模型及应用《义务教育数学课程标准（2022年版）》对尺规作图的内容及要求有所加强，其地位又得到了一定提升。

尺规作图蕴含丰富的推理，是发展学生推理能力的良好载体，而“无刻度直尺网格作图”是尺规作图的基础。

本文将在9×9的网格下讨论三种基本模型和四种复合模型。

在网格作图中，我们把两条相交直线叫做格点的“母线”。

若两条母线都是网格线，则交点叫格点；若两条母线中只有一条网格线，则交点叫次格点；若两条母线都不是网格线，则交点叫一般点。

我们要过一个点作一条线的平行线或垂线，当点是格点时，我们很轻松的通过平移完成，当点不是格点时，我们通常通过平移“生成”点的母线来完成。

一、基本作图1、过点作平行线①如图1，过C点作CD平行且等于AB解答：C是格点，只需要找到C的对应点D，因A到B的平移方式是横左2纵下3，则A到B的平移方式也是横左2纵下3。

总结：若点是格点，直接通过平移到对应点，并且平移横纵不变（下文中平移方式不变就不再强调）。

②如图2，过E点作EF平行且等于AB解答：E是次格点，先找到母线AC的对应母线BD，再找到E的对应点F。

总结：若点是次格点，先通过平移非网格线的那条母线到对应母线，再找到对应点。

③如图3，过E点作EF平行且等于AB解答：E是一般点，先找到两条母线的对应母线，再找到E的对应点F。

总结：若点是一般点，先通过平移两条母线到对应母线，再找到对应点。

变式：如图4，过E点作AB的平行线交BC于点F解答：我们除了用平移的方法作平行线，还可以利用X、A型相似作平行。

因为E是AC的一个三等分点，可以先连接BC，再利用相似找BC对应的三等分点F。

2、过点作垂线①如图5，过C点作CD垂直且等于AB解答：C是格点，只需要找到C的对应点D，因A到B的平移方式是横左2纵下3，则C到D的平移方式是横左3纵上2。

总结：若点是格点，直接通过旋转得到对应点，并且旋转横纵交换。

②如图6，过E点作EF垂直且等于AB解答：E是次格点，先过A点作AB的垂线AC（横纵交换），再过次格点E点作AC的平行线EF。

(如图*根据矩形对角线的性质找到"# 的中图)点0再根据正方形的弦图模型得到"# 的垂直平分 线.- 则与"$ 的交点即为点,!
)与面积有关的作图
图*
!面积为常数可根据底边和高的值解决作法不唯一!
"三角形面积相等可利用中线的性质或平行线间距离处处相等解决!
例如如图在由边长都为!的小正方形组成的网格中"# 两点都在格点上用无刻度直尺完成作图
"中线可利用矩形的对角线互相平分的性质作得!
#垂线可以通过构造"#$的角或利用弦图模型作得!
$角平分线可根据等腰三角形三线合一或菱形对角线互相平分以及构造全等作得!
例如如图在%&%网格中""#$ 的三个顶点都在格点上用无刻度直尺完成作图
%作出线段"# 的平行线$%且点% 在格点上
则 所以 ()*$$*&#$0*&#!")* "*0!% "*&! $*0!
设 的延长线与 交于点 则 #$*&!#")*# 0!
*&
, ",0*%
所以 又因为 所 ",$* $*$,# $*0!#")*#
$*-0#%)*
以 综上点 $,&!#")*# , 即为题中所求点-#
进阶训练
不包括边界使得

1"#$* ' (!1""#$ !
如图在 '! %&%网格中四边形"#$* 的顶点在格点上用无刻度直尺在边"# 上作一点.使得
&".*' &#.$!

无刻度直尺作图专题1．如图，在每个小正方形的边长为1的网格中，点A ，B ，C 均在格点上． （1）AB 的长等于 ；（2）在ABC ∆的内部有一点P ，满足::1:2:3PAB PBC PCA S S S ∆∆∆=，请在如图所示的网格中，用无刻度．．．的直尺，画出点P ，并简要说明点P 的位置是如何找到的（不要求证明） ．【答案】解：（1）AB =．（2）如图AC 与网格相交，得到点D 、E ，取格点F ，连接FB 并且延长，与网格相交，得到M ，N ，G ．连接DN ，EM ，DG ，DN 与EM 相交于点P ，点P 即为所求．2．如图，六个完全相同的小长方形拼成了一个大长方形，AB是其中一个小长方形的对角线，请在大长方形中完成下列画图，要求：①仅用无刻度直尺，②保留必要的画图痕迹．（1）在图1中画出一个45︒角，使点A或点B是这个角的顶点，且AB为这个角的一边；（2）在图2中画出线段AB的垂直平分线．【答案】解：（1）如图所示，45∠=︒．(AB、AC是小长方形的对角线）．ABC（2）线段AB的垂直平分线如图所示，3．如图，已知正七边形ABCDEFG，请仅用无刻度的直尺，分别按下列要求画图．（1）在图1中，画出一个以AB为边的平行四边形；（2）在图2中，画出一个以AF为边的菱形．【答案】解：（1）连接AF、BE、CG，CG交AF于M，交BE于N．四边形ABNM是平行四边形．（2）连接AF、DF，延长DC交AB的延长线于M，四边形AFDM是菱形．4．如图，在四边形ABCD中，//AB CD=，E为AB的中点，请仅用无刻度的直AB CD，2尺分别按下列要求画图（保留画图痕迹）．（1）在图1中，画出ABD∆的BD边上的中线；（2）在图2中，若BA BD∆的AD边上的高．=，画出ABD【答案】解：（1）如图1所示，AF即为所求：（2）如图2所示，BH即为所求．5．在ABC=，点A在以BC为直径的半圆内．请仅用无刻度的直尺分别按下列∆中，AB AC要求画图（保留画图痕迹）．（1）在图1中作弦EF，使//EF BC；（2）在图2中以BC为边作一个45︒的圆周角．【答案】解：（1）如图1，EF为所作；（2）如图2，DBC∠为所作．6．如图，在正方形网格中，ABC∆的顶点在格点上．请仅用无刻度直尺完成以下作图（保留作图痕迹）．'''；（1）在图1中，作ABC∆关于点O对称的△A B C（2）在图2中，作ABC∆绕点A顺时针旋转一定角度后，顶点仍在格点上的△AB C''．'''即为所求．【答案】解：（1）如图1中，△A B C（2）如图2中，△AB C''即为所求．。

【中考专题】⽆刻度直尺作图
写在前⾯
距离中考的时间越来越近了，为了帮助⼴⼤初三考⽣能在未来的中考中取得好成绩，笔者开设了《中考2021》专题突破的系列专栏，结合⾃⾝收集的好题与优质公众号的内容，以及笔者的《领跑数学中考⼆轮专题复习》，对⼀些热门中考内容作⼀个整理，今天分享专题—— ⽆刻度直尺作图！
原题再现
已知正五边形 ABCDE，请仅⽤⽆刻度直尺。

(1)作出正五边形的中⼼
(2)作出以DE为边的菱形
(3)过E点作出CD的垂线
01
正五边形是轴对称图形，求作正五边形的中⼼，根据正五边形的轴对称性，故作出它的两条对称轴其交点即为中⼼，如上图，连接EC，BD交于点G，连接AG，再连接AC与BD交于点H，连接EH，则EH与AG的交点O即为正五边形的中⼼。

02
连接AC，BD，EB交于点F，G，则四边形AEDG和四边形FEDC为菱形。

03
作正五边形的对称轴AP，EL，BK，连接KL交EP于N，连接BE交AP于点M，连接MN交CD延长线于点W，则EW⊥CD。

无刻度直尺下的几何作图技巧与方法浅谈仅用无刻度直尺的几何作图题的教与学在几何作图题中，如何利用无刻度直尺完成作图是一个重要的问题。

本文将从理解基本概念、掌握基本作图方法、理解尺规作图规则、培养作图技巧、培养解题思维、掌握辅助线作法、熟悉图形性质和练习复杂图形等方面，浅谈仅用无刻度直尺的几何作图题的教与学。

理解基本概念几何作图题中的基本概念包括点、线、角、多边形等。

要理解这些基本概念，可以通过画图的方式加深理解。

例如，通过在纸上画出多个点，可以更好地理解点的概念；通过绘制多条直线，可以更好地理解直线的概念及性质；通过画三角形、四边形等，可以更好地理解多边形的概念及其性质。

掌握基本作图方法掌握基本的作图方法是解几何作图题的基础。

基本的作图方法包括直线、射线、圆弧等作图。

对于这些基本作图方法，除了要掌握其基本原理和步骤外，还要注意如何利用无刻度直尺完成作图。

例如，在画直线时，可以利用直尺的边缘来帮助我们画出直线；在画圆弧时，可以利用圆规和无刻度直尺来共同完成。

理解尺规作图规则尺规作图规则是几何作图中的重要内容。

要理解并掌握这些规则，包括线段的中点、倍长、截短等作图方法。

在用无刻度直尺完成这些作图时，可以利用直尺的边缘作为参考，帮助我们准确地完成作图。

培养作图技巧通过练习复杂图形，可以掌握更多的作图技巧，如角度的测量、线的平行和垂直等。

在练习时，要注意观察图形中各个元素之间的关系，以及如何利用这些关系来确定作图的步骤和方案。

培养解题思维在解决几何作图题时，需要培养解题思维，通过读题和分析，确定作图步骤和方案。

要善于利用已知条件和图形中的隐含条件，运用所学知识来解决问题。

同时，要注意思考问题的方法和策略，以及如何避免常见的错误和陷阱。

掌握辅助线作法在遇到难以完成的几何作图题时，可以添加辅助线来帮助解题。

因此，掌握辅助线的作法也是非常关键的。

在添加辅助线时，需要注意以下几点：首先，要分析图形中缺少哪些元素，需要添加什么样的辅助线；其次，要注意辅助线的位置和长度；最后，要运用所学知识来证明所添加的辅助线是正确的。

解：(1)如图①， 以A为端点， 过DE与BC的交点 作射线，与圆交于 点F，线段AF即为所求 ；
图Z2－13
28
5．【2017·吉安模拟】请仅用无刻度的直尺画图：
(2)如图②，AB，CD是圆的两条弦，AB＝CD且不相互平行
，画出圆的一条直径．
解：(2)如图②，延长BA，DC交于一 点，连接BC，AD交于一点，过这两 点作直线， 与圆交于点M，N， 线段MN即为所求．
6
|针对训练| 1．在?ABCD中，点E在AD上，DE＝CD，请仅用无刻度的
直尺，按要求作图(保留作图痕迹)． (1)在图Z2－2①中，画出∠C的平分线； (2)在图②中，画出∠A的平分线．
7
2．【2015·江西模拟】如图Z2－3，在△ABC和△DCB中，
∠A＝∠D＝90°，AC＝BD，AC与BD相交于点O.仅用无刻度
图Z2－8
18
【点拨交流 】 1．图形中的圆有哪些基本性质？ 2．由(1)中的AC＝BC，你能得到什么？ 3．平分三角形面积的方法有哪些？
19
【解题思路】
20
|针对训练| 1．【2013·江西】如图Z2－9，AB是半圆的直径，图①中
，点C在半圆外；图②中，点C在半圆内．请仅用无刻度的直 尺按要求画图．
图Z2－9
22
2．【2016·鹰潭联考】用无刻度的直尺作图，保留作图痕迹 ，分别作出图中∠AOB的平分线：
(1)如图Z2－10①，∠AOB的两边与一圆切于点A，B，点M ，N是优弧AB的三等分点；
(2)如图②，∠AOB的两边与一圆交于点A，B，M，N，且 AM＝BN.
解：如图所示．
图Z2－10
23
图Z2－13
29
6．【2017·江西样卷】请仅用无刻度的直尺，用连线的方法在 图Z2－14①，图②中分别过圆外一点 A作出直径BC 所在直线的 垂线．

无刻度直尺作图训练一约定概念：网格由全等的小正方形组成，边长为“1”。

网格线的交点叫格点，端点是格点的线段叫格点线段.端点是格点的三角形（矩形）叫格点三角形（矩形）.无刻度直尺作图，直尺只能过两点作直线、射线、线段，不能测量线段长度，不能作特殊角（如直角）.非格点通常是通过格点线段与格点线段相交来确定.格点线段：1、任意格点线段的长可求，在网格线上的格点线段长为正整数；2、不与网格线平行或垂直的格点线段可以看成格点Rt△的斜边（两直角边为正整数）或看成格点矩形的对角线（长宽均在网格线且为正整数）.注意：为便于研究，以下作图均在边长为1 的小正方形组成的网格中，A、B、C、D 均为格点，利用网格，按照题中要求仅用无刻度的直尺作图.一、数量关系——分割线段例1.①作线段AB的中点②求作点P，使得AP：PB=1:2；③求作点P，使得AP：PB=13:6.总结：作格点线段的中点，可通过; 按比例分割线段，可通过.二、位置关系1.作已知格点线段的平行线1.1过格点作已知格点线段的平行线例2.请用无刻度的直尺在网格中完成下列画图，保留连线的痕迹，不要求说明理由．（1）找一格点M 使CM∥AB，且CM=AB;（2）找一格点N 使DN∥AB，且DN=AB;总结：1.2过非格点作已知格点线段的平行线例 3.如图，四边形ABCD 的顶点在格点上，点 E 是边DC 与网格线的交点．请用无刻度的直尺在网格中完成下列画图，保留连线的痕迹，不要求说明理由：过点E 画线段EM，使EM∥AB，且EM＝AB．总结：变式1.如图，四边形ABCD 的顶点在格点上，点E 是边AB与网格线的交点．请用无刻度的直尺在网格中完成下列画图，保留连线的痕迹，不要求说明理由:过点E 画线段EM，使EM∥CD，且EM＝CD．2.作已知线段的垂线2.1过格点作已知格点线段的垂线例4.如图，请用无刻度的直尺在网格中完成下列画图，保留连线的痕迹，不要求说明理由．（1）找一格点M 使CM⊥AB，且CM=AB;（2）找一格点N 使DN⊥AB，且DN=AB;（3）作AB 的垂直平分线.总结：2.2过非格点作已知格点线段的垂线例 5.用无刻度的直尺在网格中完成下列画图，保留连线的痕迹，不要求说明理由．如图，找一点M，使EM⊥CD，且EM=CD总结：练习1（2020 武汉五调）如图，△ABC 的顶点在格点上，仅用无刻度尺的直尺在给定网格中画图，画图过程用虚线表示，画图结果用实线表示，按步骤完成下列问题：（1）将边BC 绕点C 顺时针旋转90°得到线段CD（2）画边AC 的中点E（3）连接DE 并延长交BC 于点F，直接写出CF：BF 的值（4）在AB 上画点G，连接FG，使FG//CD反思1、格点线段中点——构造平行四边形，利用平行四边形对角线互相平分2、按比例分割格点线段——构造X 型相似三角形，化斜为直3.过一点作格点线段的平行线①过格点——利用平移作平行②过非格点——确定点的位置，将点的平移转化为线段的平移4.过一点作格点线段的垂线段①过格点——先将线段绕端点旋转90°得垂直，转化为过格点做平行②过非格点——先将线段绕端点旋转90°得垂直，转化为过非格点做平行数学思想：转化思想补充练习：变式：1.如图，△ABC 的顶点在格点上，仅用无刻度的直尺在给定网格中画图，画图过程用虚线表示，画图结果用实线表示，按步骤完成下列问题：（1）画出BC 关于AC 对称的线段CD；（2）画出AC 的中点E；（3）连接DE 并延长交AC 于点F，直接写出AF：BF 的值；（4）在AC 上画点G，连接FG，使FG//BC.2.（本题8 分）如图是由边长为1 的小正方形构成的网格，每个小正方形的顶点叫格点，△ABC的顶点都在格点上，仅用无刻度的直尺在网格中画图（保留作图连线痕迹），并回答问题.(1)在BC 的右边找格点D，连AD，使AD 平分∠BAC.(2)若AD 与BC 交于E ，直接写出BE:CE 的值.(3)找格点F，连EF，使EF⊥AB 于H.(4)在AC 上找点G，连EG，使EG∥AB.3.（本题8 分）如图是由边长为1 的小正方形构成的网格，每个小正方形的顶点叫做格点，点A、B、C、F 都是格点．用无刻度的直尺在给定网格中画图，画图过程用虚线表示，画图结果用实线表示(1)在图1 中① 画线段AD，使AD∥BC，且AD 1 BC2② 画∠APB＝45°③ 在线段AB 上画点E，使AE＝2(2)在图2 中，画点M，使点M 与点F 关于AB 对称4.（本题8 分）如图是由边长为1 的小正方形构成的网格，每个小正方形的顶点叫做格点．线段AB 的端点在格点上，仅用无刻度尺的直尺在给定网格中画图，画图过程用虚线表示，画图结果用实线表示，按步骤完成下列问题：(1)将线段AB 绕点B 逆时针旋转90°得到线段BC(2)在AC 上取点D 使AD=2CD(3)在BC 上取点E，使∠AEB=∠DEC(4)直接写出tan∠EAC=5.（本题8 分）.如图，在7×7 正方形网格中的每个小正方形边长都为1 个单位长度，我们把每个小正方形的顶点称为格点，点A、B、C 都为格点，且点A（1，2），请分别仅用一把无刻度的直尺画图；（1）过点C 画一条线段AB 的平行线段CD，直接写出格点D 的坐标；（2）过点C 画一条线段AB 的垂直线段CE，直接写出格点E 的坐标；（3）作∠DCE 的角平分线CF，直接写出格点F 的坐标；（4）作∠ABM，使∠ABM=45°，直接写出格点M 的坐标；6.(8分)如图是7×7个边长为1的正方形组成的网格，每个小正方形的顶点均为格点，△ABC的三个顶点A、B、C 均为格点，仅用无刻度的直尺按照下列步骤作图，作图过程中的线用虚线，作图结果用实线表示.(1)在AB 上取点F，使得CF⊥AB；(2)直接写出AF的值；BF(3)在BC 上取一点M，使得FM∥AC.7. (8 分)如图，在平面直角坐标系中，A(－2，2)，B(1，4)，C(1，2)，D(2，0)，E(－1，－2).(1)将△ABC 绕平面内一点P 旋转，得到△DEF，使A、B 分别与点D、E 对应，请画出△DEF，并直接写出点P、F 的坐标分别为：(2)给出定义：三角形一边上的点将该边分为两段，若这两条线段的积等于这个点到该边所对顶点连线段的平方，则称这个点为三角形该边的“奇异点”，例如：点M 在△ABC 的边BC 上，若BM·CM＝AM²，则点M 是△ABC 中BC 边的“奇异点”.【解决问题】仅用无刻度的直尺画出(1)中的△DEF的边DE 的“奇异点”Q，并直接写出EQ的值. DQ8..(8 分)如图，四边形ABCD 中，AD∥BC，BC＝2AD，AB＝CD，AC、BD 交于点O，仅用刻度的直尺按下列步骤作图，作图过程中的线用虚线，作图结果用实线表示.(1)过点O 作OE⊥BC，垂足为E；(2)连接AE 交BD 于F，在AB 上取一点M，使FM∥BC；(3)在BD 上取一点N，使得EN∥AC；(4)过点A 作AH⊥BC，垂足为H.9.（本题8 分）如图是由边长为1 的小正方形构成的网格，每个小正方形的顶点叫做格点．△ABC 的顶点在格点上. 仅用无刻度尺的直尺在给定网格中画图，画图过程用虚线表示，画图结果用实线表示，按步骤完成下列问题：（1）作△ABC 的高AD；（2）在BC 边上找一点P，使tan∠CAP=2/5（3）过点C 作AB 的垂线.10.(8 分)如图，在边长为1 个单位长度的小正方形组成的网格中，按要求利用无刻度的直尺画图(保留作图痕迹).(1)在网格中，在△ABC 的下方取格点E，使四边形ABEC 是轴对称图形；(2)找一点F，使点F 到点A、B、C 的距离相等；(3)在BC 边上找一点D，使∠BAD＝45°，请直接写出DF 的长为.AB C11. (8 分)如图，已知 A （2，0），B （1，3），用无刻度的直尺在网格上按要求画图. (1) 将线段 AB 绕点 A 逆时针旋转 90°至 AM ，则 M 点的坐标为 ； 将线段 AB 绕点 B 顺时针旋转 90°至 BN ，则 N 点的坐标为 ； (2) 在 AM 上找点 E ，在 BN 上找点 F ，使得矩形 MNFE 的面积为 3； (3) 在 AM 上找点 C ，使ME 3 . AC 412.（本题 8 分）如图是由边长为 1 的小正方形构成的网格，每个小正方形的顶点叫做格点．△ABC 的顶点在格点上，仅用无刻度尺的直尺在给定网格中画图，画图过程用虚线表示，画图结果用实线表示，完成下列问题：(1) tan ∠FCA ＝ ； (2) 将边 BA 绕点 A 顺时针旋转 2∠FCA 得到线段 AD ，则∠CAD ＝ ；(3) 画出△ADC 的外接圆的圆心 O ； (4) 在 AD 上确定一点 G ，使 GF ＝GD ．yxAOB。