专题：无刻度直尺作图

中考数学压轴题之无刻度直尺作图、网格点作图技巧详解仅用无刻度直尺作图和网格点作图问题已成为各地中考热门考点，近年来在江西、武汉、天津等地中考中均以压轴题出现，其难度一般会超过单纯的证明题或计算题。

这类题型主要考察同学们对几何图形性质的熟悉程度，还有同学们平时方法和技巧的掌握。

常见的考察点有：特殊点问题、特殊角问题、垂直问题、平行问题、角平分线问题、与圆有关的问题等。

无刻度直尺的作用只有一个：将已知的两点连线。

我们要充分利用格点的作用：取点、平行等。

下面对各类常见题型的技巧进行了分类总结。

一、特殊点问题例1：在下面网格图中用无刻度直尺作出线段AB的中点。

分析与解：利用“8”字型平行线分线段成比例、平行四边形对角线互相平分等性质，图中不同颜色的线均可将AB平分。

例2：在下面网格图中用无刻度直尺作出线段AB的中点，其中A为格点，B为任意点。

分析与解：如图，取格点C，连接CB并延长交网格线于E,取AC、AE与网线的交点D、F（即中点），连接DF交AB于G，则G我们利用中位线及平行线分线段成比例的性质进行了优化处理。

例3：在下面网格图中，在线段AB 上找一点C ，使AB AC 31=。

方法1方法2 方法3分析与解：方法1和方法2都利用了网格线平行的性质，通过“8”字型模型，构造1：2的相似比例，从而将线段AB 分为1：2两段。

方法3利用了重心的性质，AB 和EF 为BED ∆的两条中线，所以C 为BED ∆的重心。

二、特殊角问题例4：在下面网格图中找格点C ，使O BAC 45=∠。

分析与解：利用“12345”模型，即若βα、均为锐角，且31tan ,21tan ==βα，则O 45=+βα。

例5：如下图，利用无刻度直尺在线段MN 上找一点Q ，使O AQB 45=∠。

分析与解：O AQB 45=∠，典型定弦定角问题。

注意到O AMB 90=∠，所以点Q 在以M 为圆心，MA 长为半径的圆上，故2=MQ 。

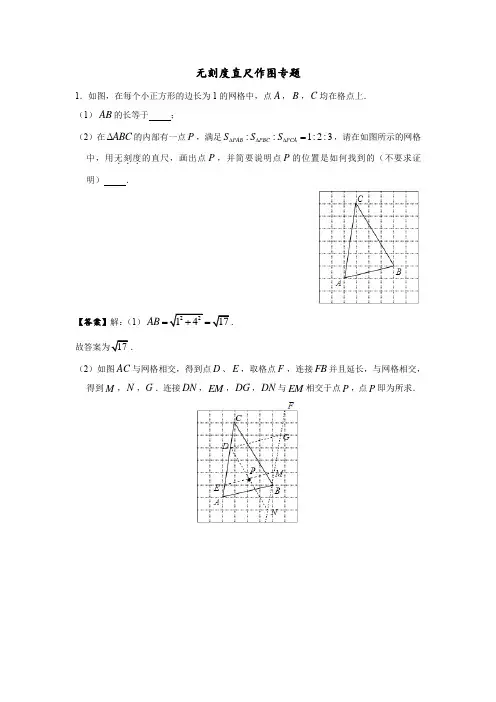
无刻度直尺作图专题1．如图，在每个小正方形的边长为1的网格中，点A ，B ，C 均在格点上． （1）AB 的长等于 ；（2）在ABC ∆的内部有一点P ，满足::1:2:3PAB PBC PCA S S S ∆∆∆=，请在如图所示的网格中，用无刻度．．．的直尺，画出点P ，并简要说明点P 的位置是如何找到的（不要求证明） ．【答案】解：（1）AB =．（2）如图AC 与网格相交，得到点D 、E ，取格点F ，连接FB 并且延长，与网格相交，得到M ，N ，G ．连接DN ，EM ，DG ，DN 与EM 相交于点P ，点P 即为所求．2．如图，六个完全相同的小长方形拼成了一个大长方形，AB是其中一个小长方形的对角线，请在大长方形中完成下列画图，要求：①仅用无刻度直尺，②保留必要的画图痕迹．（1）在图1中画出一个45︒角，使点A或点B是这个角的顶点，且AB为这个角的一边；（2）在图2中画出线段AB的垂直平分线．【答案】解：（1）如图所示，45∠=︒．(AB、AC是小长方形的对角线）．ABC（2）线段AB的垂直平分线如图所示，3．如图，已知正七边形ABCDEFG，请仅用无刻度的直尺，分别按下列要求画图．（1）在图1中，画出一个以AB为边的平行四边形；（2）在图2中，画出一个以AF为边的菱形．【答案】解：（1）连接AF、BE、CG，CG交AF于M，交BE于N．四边形ABNM是平行四边形．（2）连接AF、DF，延长DC交AB的延长线于M，四边形AFDM是菱形．4．如图，在四边形ABCD中，//AB CD=，E为AB的中点，请仅用无刻度的直AB CD，2尺分别按下列要求画图（保留画图痕迹）．（1）在图1中，画出ABD∆的BD边上的中线；（2）在图2中，若BA BD∆的AD边上的高．=，画出ABD【答案】解：（1）如图1所示，AF即为所求：（2）如图2所示，BH即为所求．5．在ABC=，点A在以BC为直径的半圆内．请仅用无刻度的直尺分别按下列∆中，AB AC要求画图（保留画图痕迹）．（1）在图1中作弦EF，使//EF BC；（2）在图2中以BC为边作一个45︒的圆周角．【答案】解：（1）如图1，EF为所作；（2）如图2，DBC∠为所作．6．如图，在正方形网格中，ABC∆的顶点在格点上．请仅用无刻度直尺完成以下作图（保留作图痕迹）．'''；（1）在图1中，作ABC∆关于点O对称的△A B C（2）在图2中，作ABC∆绕点A顺时针旋转一定角度后，顶点仍在格点上的△AB C''．'''即为所求．【答案】解：（1）如图1中，△A B C（2）如图2中，△AB C''即为所求．。

【中考专题】⽆刻度直尺作图
写在前⾯
距离中考的时间越来越近了，为了帮助⼴⼤初三考⽣能在未来的中考中取得好成绩，笔者开设了《中考2021》专题突破的系列专栏，结合⾃⾝收集的好题与优质公众号的内容，以及笔者的《领跑数学中考⼆轮专题复习》，对⼀些热门中考内容作⼀个整理，今天分享专题—— ⽆刻度直尺作图！
原题再现
已知正五边形 ABCDE，请仅⽤⽆刻度直尺。

(1)作出正五边形的中⼼
(2)作出以DE为边的菱形
(3)过E点作出CD的垂线
01
正五边形是轴对称图形，求作正五边形的中⼼，根据正五边形的轴对称性，故作出它的两条对称轴其交点即为中⼼，如上图，连接EC，BD交于点G，连接AG，再连接AC与BD交于点H，连接EH，则EH与AG的交点O即为正五边形的中⼼。

02
连接AC，BD，EB交于点F，G，则四边形AEDG和四边形FEDC为菱形。

03
作正五边形的对称轴AP，EL，BK，连接KL交EP于N，连接BE交AP于点M，连接MN交CD延长线于点W，则EW⊥CD。

深入了解无刻度直尺在几何作图中的应用无刻度直尺是一种在几何作图中常用的工具，它能够帮助我们进行精确的测量和绘制。

本文将深入探讨无刻度直尺在几何作图中的应用，包括常用的绘制线段、角度和平行线等几何图形。

通过对这些应用的了解，我们能够更好地掌握几何作图的技巧和方法。

一、绘制线段在几何作图中，经常需要绘制一定长度的线段。

无刻度直尺虽然没有具体的刻度，但它却可以通过两点之间的距离来确定线段的长度。

我们可以将无刻度直尺的一端对准线段的起点，然后用另一只手握住直尺的另一端，将直尺移动到线段的终点位置。

移动直尺时，可以用目测和手感来保持线段的长度一致，然后用铅笔在直尺旁边划一条与直尺重合的线段。

这样就完成了线段的绘制。

二、绘制角度在几何作图中，绘制角度是非常常见的操作。

无刻度直尺可以辅助我们精确地绘制各种角度。

例如，要绘制一个90度的直角，我们可以先将无刻度直尺的一端对准一条水平直线，然后用铅笔在直尺的一侧做一个标记。

接下来，将直尺绕着这个标记点旋转90度，使直尺的一条边与水平直线重合，再用铅笔在直尺另一侧划一条与直尺重合的直线，这样就得到了一个精确的直角。

除了绘制直角，无刻度直尺还能帮助我们绘制其他角度。

例如，要绘制一个等边三角形，我们可以先将无刻度直尺的一边对准一条水平直线，然后将直尺固定在这个位置，再将直尺的另一边移到一个合适的位置。

移动直尺时，可以用目测和手感来保持直角的一致，然后再用铅笔在直尺的另一侧划一条直线，这样就得到了一个等边三角形。

三、绘制平行线在几何作图中，绘制平行线也是经常遇到的问题。

通过无刻度直尺，我们可以很容易地绘制出与已知直线平行的新直线。

例如，要绘制一条与已知直线平行的直线，我们可以先将无刻度直尺的一边对准已知直线，然后用铅笔在直尺的另一侧划一条直线。

接着，将直尺移开，再用直尺的一边对准开始划线的点，用铅笔在直尺的另一侧划一条与初始直线平行的直线，这样就绘制出了一条平行线。

除了绘制平行线，无刻度直尺还可以帮助我们绘制相交直线上的垂直线。

掌握无刻度直尺在几何作图中的应用技巧直尺是几何学中常用的工具之一，用于绘制直线和测量长度。

无刻度直尺是一种没有刻度的直尺，可以准确地划线和测量，但需要掌握一些技巧才能正确使用。

掌握无刻度直尺在几何作图中的应用技巧对于学习几何学和解决几何问题非常重要。

本文将介绍几种常见的无刻度直尺的应用技巧。

一、使用无刻度直尺绘制直线无刻度直尺没有刻度，但我们可以利用直角来绘制垂直或水平的直线。

首先，将直尺的一边与绘图纸上的一条直线对齐，并确定直尺的一端与绘图纸上的一个点相切。

然后，将另一边轻轻地与直尺上的直角对齐，并保持直尺与绘图纸保持紧密接触。

这样，我们就可以绘制一条垂直或水平的直线。

二、使用无刻度直尺绘制等边三角形等边三角形的三条边长度相等。

使用无刻度直尺绘制等边三角形的关键是确定等边三角形的边长。

首先，选择无刻度直尺上的一个固定长度，将直尺的一端放置在绘图纸上的一个点上。

然后，保持直尺与绘图纸保持紧密接触，将直尺转动至一个合适的角度，使直尺的另一端与绘图纸上的一点相切。

这样，我们就可以绘制等边三角形的一条边。

接下来，使用相同的方法绘制另外两条边，确保它们的长度与第一条边相等即可。

三、使用无刻度直尺绘制角度使用无刻度直尺绘制角度需要注意的是，无刻度直尺上没有刻度，无法准确测量角度的大小。

因此，我们需要通过其他的方法来绘制所需的角度。

一种常用的方法是使用三角板或者其他角度工具来辅助绘制。

首先，确定要绘制的角度的大小，并选择一个合适的角度工具。

将角度工具的一边对齐于绘图纸上的一条直线，并确保角度工具上的角度大小与要绘制的角度相等。

然后，将无刻度直尺的一边与角度工具的另一边对齐，并保持直尺与绘图纸保持紧密接触。

这样，我们就可以在绘图纸上绘制出所需的角度。

四、使用无刻度直尺测量线段长度无刻度直尺没有刻度，无法直接测量线段的长度。

但我们可以通过比较两条线段的长度来大致测量线段的长度。

使用无刻度直尺测量线段长度的关键是选择一个已知长度的线段作为基准。

掌握无刻度直尺在几何作图中的方法与技巧直尺作为几何作图的基本工具之一，在绘制线段、角度等几何图形的过程中起到重要作用。

传统的刻度直尺在一些情况下可能不够精确，而无刻度直尺则可以克服这一限制，能够更加准确地绘制图形。

本文将介绍无刻度直尺在几何作图中的方法与技巧，帮助读者掌握这一重要工具的使用。

一、无刻度直尺简介无刻度直尺，又称为不透明直尺或者不透明尺，是一种没有刻度且不透明的直尺。

它通常由透明或半透明材料制成，边缘呈直线状，并且具备一定的刚性。

由于无刻度直尺没有刻度标记，所以无法直接读取长度，但是可以用来测量、绘制线段、角度等几何图形。

二、使用无刻度直尺作图的方法1. 绘制直线要绘制一条直线，首先需要选择两个明确的点作为起点和终点。

将无刻度直尺平放在绘图纸上，将起点和终点对准无刻度直尺的边缘上，并且保持直尺的位置不变，然后用一支铅笔或者细线笔沿着直尺的边缘缓慢滑动，从而绘制出一条直线。

2. 绘制平行线若要绘制与已有直线平行的直线，可以利用无刻度直尺的边缘作为导向。

首先，将直尺平放在已有直线上，调整角度，使直尺与直线边缘平行。

然后，在直尺的边缘上选择一个点作为起点，然后保持直尺不动，沿着边缘绘制出一条平行线。

3. 绘制垂直线绘制与已有直线垂直的直线时，同样可以利用无刻度直尺的边缘作为导向。

将直尺平放在已有直线上，调整角度，使直尺与直线边缘垂直。

然后，在直尺的边缘上选择一个点作为起点，保持直尺不动，沿着边缘绘制出一条垂直线。

4. 绘制角度使用无刻度直尺绘制角度时，需要首先确定一个顶点，然后将直尺放置在该顶点上，并且调整角度。

接下来，在直尺的边缘上选择两个点，作为角度的两条边，保持直尺的位置不变，沿着边缘绘制出所需的角度。

三、无刻度直尺在几何作图中的技巧1. 使用透明胶带或者可移动标记由于无刻度直尺没有刻度标记，有时可能难以准确测量和标记长度。

此时，可以使用透明胶带或者可移动标记来辅助测量和标记。

将透明胶带粘贴在直尺边缘，标出所需长度，或者使用可移动标记夹在直尺上，便于测量和标记长度。

深入了解无刻度直尺在几何作图中的运用在几何学中，作图是一个重要的环节，它帮助我们将抽象的数学概念转化为可视化的图形，以便更好地理解和应用。

在作图中，直尺是一种常用的工具，它用来绘制直线和测量长度。

然而，传统的直尺通常带有刻度，限制了我们对非整数长度的精确测量。

为了克服这一限制，无刻度直尺应运而生，它为我们提供了更大的灵活性和准确性。

本文将深入了解无刻度直尺在几何作图中的运用。

一、无刻度直尺的特点及优势无刻度直尺是一种没有刻度的直尺，常见的有钢尺和透明直尺。

相比传统的带刻度直尺，无刻度直尺具有以下特点及优势：1. 灵活性：无刻度直尺没有固定的刻度，可以自由地在任意长度上进行绘制和测量，从而更好地符合实际需求。

2. 精确性：由于没有刻度的限制，无刻度直尺可以以更高的精确度进行测量，可以满足更高标准的要求。

3. 可视性：透明直尺的透明性使得我们可以更清楚地观察到被测量对象的细节，提高了作图过程的可视性和准确性。

二、无刻度直尺在直线绘制中的运用在几何作图中，直线是一个基本的图形元素，无刻度直尺在直线绘制中起着至关重要的作用。

下面将介绍无刻度直尺在直线绘制中的两种常见方法。

1. 两点确定直线：给定两个点A和B，需要在纸上绘制经过这两个点的直线。

使用无刻度直尺，我们可以按照以下步骤进行：a. 把直尺平放在纸上，使其边缘经过点A。

b. 把直尺保持在相同位置，将其边缘移动至点B。

c. 保持直尺的位置不变，用铅笔在纸上沿着直尺的边缘绘制直线AB。

通过这种方法，我们可以准确地绘制出经过给定两点的直线。

2. 点和斜率确定直线：给定一个点A和直线的斜率k，需要在纸上绘制经过该点且具有给定斜率的直线。

使用无刻度直尺，我们可以按照以下步骤进行：a. 把直尺平放在纸上，使其边缘经过点A。

b. 在直尺上选择一个合适的长度，表示斜率的分母。

c. 在直尺上找到相应的位置，表示斜率的分子。

d. 将直尺的边缘移动至点A，并将其边缘旋转至与纸上的点对齐。