振动力学第二章第二节单自由度系统的受迫振动
- 格式:ppt
- 大小:2.85 MB
- 文档页数:63





习 题2-1已知系统的弹簧刚度k =800 N/m ,作自由振动时的阻尼振动周期为1.8s ,相邻两振幅的比值12.41=+i i A A ,若质量块受激振力t t F 3cos 360)(=N 的作用,求系统的稳态响应。
解:由题意,可求出系统的运动微分方程为t mxn x p x n 3cos 36022=++ 得到稳态解)3cos(α-=t B x其中m kB B B 45.03604)1(022220==+-=λζλ222122tg λζλωωα-=-=n p n 由d nT i iA A e 2.41===+η489.3π2797.0ln 8.1ln ======dd dd dT p T n T nT ηη 又22n p p n d -=有579.3222=+=n d n p n p p45.51255.1298.0374.0838.01838.0223.02tg 103.1408.045.0838.0223.04)838.01(45.0223.0579.3797.0838.0579.332222===-⨯⨯===⨯⨯+-=======ααζωλB p n p n n所以 x =1.103 cos(3t -51︒27')2-2一个无阻尼弹簧质量系统受简谐激振力作用,当激振频率ω1 =6rad/s 时,系统发生共振;给质量块增加1 kg 的质量后重新试验,测得共振频率ω2 =5.86rad/s ,试求系统原来的质量及弹簧刚度。
解:设原系统的质量为m ,弹簧常数为k 由m kp n =,共振时m kp n ==1ω 所以 mk =6 ①又由 当 86.512=+==m kp n ω ② ①与②联立解出 m =20.69 kg ,k =744.84 N/m2-3总质量为W 的电机装在弹性梁上,使梁产生静挠度st δ,转子重Q ,重心偏离轴线e ,梁重及阻尼可以不计,求转速为ω时电机在垂直方向上稳态强迫振动的振幅。

习 题2-1已知系统的弹簧刚度k =800 N/m ,作自由振动时的阻尼振动周期为1.8s ,相邻两振幅的比值12.41=+i i A A ,若质量块受激振力t t F 3cos 360)(=N 的作用,求系统的稳态响应。
解:由题意,可求出系统的运动微分方程为t mxn x p x n 3cos 36022=++ 得到稳态解)3cos(α-=t B x其中m kB B B 45.03604)1(022220==+-=λζλ222122tg λζλωωα-=-=n p n 由d nT i iA A e 2.41===+η489.3π2797.0ln 8.1ln ======dd dd dT p T n T nT ηη 又22n p p n d -=有579.3222=+=n d n p n p p45.51255.1298.0374.0838.01838.0223.02tg 103.1408.045.0838.0223.04)838.01(45.0223.0579.3797.0838.0579.332222===-⨯⨯===⨯⨯+-=======ααζωλB p n p n n所以 x =1.103 cos(3t -51︒27')2-2一个无阻尼弹簧质量系统受简谐激振力作用,当激振频率ω1 =6rad/s 时,系统发生共振;给质量块增加1 kg 的质量后重新试验,测得共振频率ω2 =5.86rad/s ,试求系统原来的质量及弹簧刚度。
解:设原系统的质量为m ,弹簧常数为k 由m kp n =,共振时m kp n ==1ω 所以 mk =6 ①又由 当 86.512=+==m kp n ω ② ①与②联立解出 m =20.69 kg ,k =744.84 N/m2-3总质量为W 的电机装在弹性梁上,使梁产生静挠度st δ,转子重Q ,重心偏离轴线e ,梁重及阻尼可以不计,求转速为ω时电机在垂直方向上稳态强迫振动的振幅。

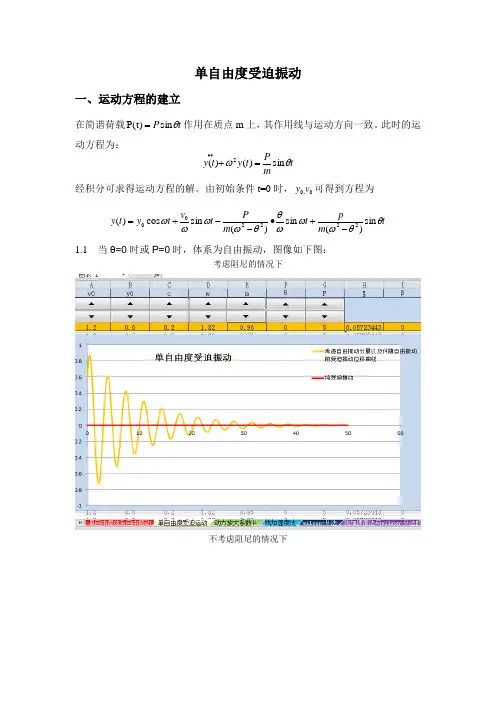
单自由度受迫振动一、运动方程的建立在简谐荷载t P θsin )t (P =作用在质点m 上,其作用线与运动方向一致。
此时的运动方程为:t mP t y t y θωsin )()(2=+∙∙ 经积分可求得运动方程的解。
由初始条件t=0时,0,0v y 可得到方程为t m p t m P t v t y t y θθωωωθθωωωωsin )(sin )(sin cos )(222200-+∙--+= 1.1 当θ=0时或P=0时,体系为自由振动,图像如下图: 考虑阻尼的情况下不考虑阻尼的情况下当P不为0,且θ不为零的情况下,体系发生受迫振动。
二、无阻尼振动单自由度体系受迫振动可分为有阻尼和无阻尼振动两种。
在模型建立过程当中,可以直接进行建立。
在运行时,只需将c=0即可。
如下图,结构在受迫振动的同时会有初位移,初速度引起的自由振动,以及动荷载激起的按结构自振频率振动的分量,即伴随自由振动。
三、有阻尼受迫振动由于有阻尼的作用,自由振动会很快的衰减掉。
在振动计算过程中,通常不考虑自由振动部分尚未完全衰减掉的过渡阶段,而只计算在这以后体系按干扰力的频率θ进行的受迫振动。
这时的振幅和频率是恒定的。
成为稳态强迫振动。
如图:3.1 振幅22-11A ωβm P ∙=,ωθβ= 由公式可见,强迫振动的振幅除与干扰力这幅P 有关外,还与ωθβ=有关。
3.1.1 ωθ<< 此时0≈=ωθβ,得st y ≈≈A 1,μ,可知与自振频率相比,频率很低的干扰力所产生的动力作用并不明显,可当静荷载处理,可认为结构为刚体或荷载并不随时间变化,不存在振动问题。
图像如下图所示3.1.2ωθ>> 此时ωθβ=是一个很大的数,st y <<<<A 1,μ。
表明当干扰力平率远大于自振频率时,动位移将远小于扰力幅值P 所产生的静位移,质体将接近静止状态,如下图:θ→3.1.3ωθ→时,放大系数和动位移的振幅A理论上将趋于无限,而实际上由于阻当ω尼的存在,振幅不会趋于无穷,但仍会远大于静位移y。


