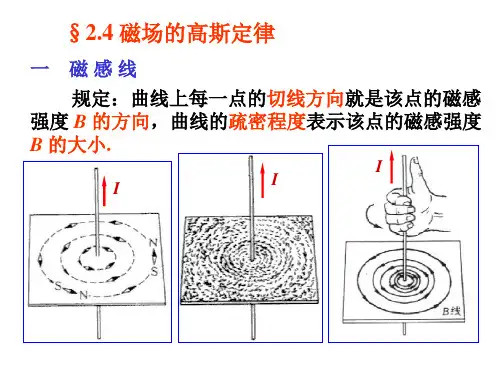
磁场高斯定理证明
- 格式:doc
- 大小:66.50 KB
- 文档页数:2



磁场中高斯定理公式磁场中的高斯定理什么是磁场中的高斯定理?磁场中的高斯定理是一种描述磁场分布的物理定律,它与电场中的高斯定理类似。
磁场中的高斯定理告诉我们,通过任意闭合曲面的磁通量等于该闭合曲面内磁场的总极化矢量。
高斯定理的数学表达式磁场中的高斯定理可以用以下数学公式来表示:∮ B · dA = μ0 * Φ其中, - ∮ 表示对整个闭合曲面的积分运算; - B 表示磁场的磁感应强度; - dA 表示曲面上的微小面积元素; - μ0 表示真空中的磁导率,其值约为× 10^-6 H/m; - Φ 表示通过闭合曲面的磁通量。
如何理解高斯定理?为了更好地理解磁场中的高斯定理,我们来看一个例子。
假设有一个无限长直导线,通过这条导线的电流为I,我们想要计算该导线所产生的磁场在某表面上的磁通量。
我们可以选择一个以导线为轴线、面积为A的柱状闭合曲面,这个闭合曲面穿过导线并覆盖了所有的磁场线。
根据高斯定理,这个柱状闭合曲面上的磁通量等于该曲面内磁场的总极化矢量。
因为该闭合曲面只有一个入口和一个出口,而且导线内部的磁场线是圆形的,所以曲面上的磁场线数是一样的。
由于磁场线在柱状闭合曲面的投影面积都是相同的,所以曲面上的磁通量也是相同的。
根据高斯定理的数学表达式,磁场的磁通量等于磁感应强度与曲面上的微小面积元素的点积之和。
所以对于这个闭合曲面,磁通量可以表示为:Φ = B * A根据高斯定理的公式:∮ B · dA = μ0 * Φ我们可以得出:B * A = μ0 * Φ从而得出导线所产生的磁场的磁感应强度为:B = (μ0 * Φ) /A这个例子展示了如何使用高斯定理来计算闭合曲面中的磁通量。
通过选择合适的曲面和断面面积,我们可以方便地计算任何形状导线所产生的磁场的磁感应强度。
总结磁场中的高斯定理是一种描述磁场分布的重要定理。
它告诉我们,通过任意闭合曲面的磁通量等于该闭合曲面内磁场的总极化矢量。

磁场中的高斯定理说明磁场的性质:对一封闭曲面来说,一般取向外的指向为正法线的指向。
这样从闭合面穿出的磁通量为正,穿入的磁通量为负。
由于磁感线是闭合线,那么穿过任一封闭曲面的磁通量一定为零。
真空静电场的高斯定理:∮EdS=(∑Q)/ε0
稳恒磁场的高斯定理:∮BdS=0
这两个结论的不同揭示了静电场和磁场的一个差异:
静电场是有源场,它的电场线不会闭合,所以对一个封闭曲面的通量不一定为0;而稳恒磁场是无源场,它的磁场线是封闭的,有多少条磁场线穿出曲面,相应就有多少条磁场线穿进曲面,所以磁场对一个封闭曲面的通量恒为0。
用比较专业的场论术语来说,就是:静电场是有源场,散度一般不为0;稳恒磁场是无源场,散度恒为0。
静电场中的环路定理:∮Edl=0(l是L的小写,不是数字1)
稳恒磁场的安培环路定律:∮Bdl=(∑I)/μ0 (∑后面的是字母i的大写)
这两个不同的结论又反映了静电场和磁场的另一个差异:
静电场是无旋场,即它的旋度恒为0,所以静电场对环路积分结果为0;
稳恒磁场是有旋场,一般旋度不为零,所以磁场对环路的积分一般不等于0。


高斯定理证明
高斯定理是电磁学中的一个重要定理,也称为高斯第一定理、高斯-奥波尔兹定理或高斯-斯托克斯定理。
它是电场、磁场和流体动力学中的基本方程之一,描述电场、磁场和流体速度的场在一个闭合曲面上的性质。
高斯定理可以用来计算电场通过一个任意形状的闭合曲面的总通量,它的数学表达式为:
∮E · dA = 1/ε₀ · ∫∫∫ρ dV
其中:
- ∮E · dA表示电场E与曲面元dA的点乘积(即电场E沿曲面法向量方向的分量与曲面元面积的乘积)之和。
- ε₀为电场中的真空介电常数,其值为8.854×10⁻¹²
C²/(N·m²)。
- ∫∫∫ρ dV表示在闭合曲面内的电荷密度ρ乘以体积元dV 之和。
高斯定理的证明分为两个步骤:
1. 假设电场E是有限个点电荷的叠加,可以根据库仑定律得到电场E与闭合曲面上各点的点乘积之和等于电荷与外部点产生的共同电势的梯度在该点上的点乘积之和。
2. 利用极限的思想,将点电荷的数量无限逼近,使得点电荷产生的电场可以看作一个连续的场,通过对电场的积分可以得到闭合曲面上的总通量。
综上所述,高斯定理的证明基于库仑定律和极限的思想,将点电荷的叠加近似为连续的电场场源,通过对电场的积分计算闭合曲面上的总通量。


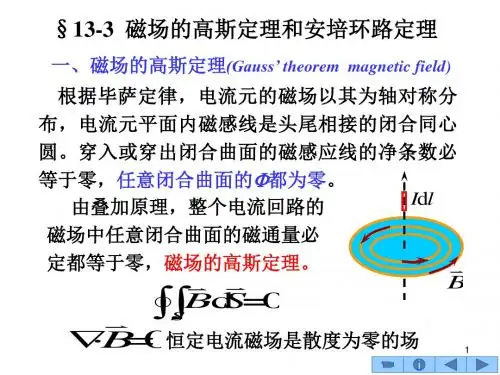

磁场高斯定理的证明
根据闭奥萨伐尔定律,单个电流元IdL产生的磁感应线是以 dL方向韦轴线的圆,如图,圆周上元磁场的数值处处相等:
在磁感应线穿入处取一面元dS1,穿出处取另一面元dS2,IdL产生的磁场通过两面元的磁感应通量分别为:
由于磁感应管呈严格的圆环状,其正截面处处相等,故,
所以,即。
所以高斯定理对单个电流元成立。
根据磁场叠加原理,任意载流回路产生的总磁场B是各电流元产生的元磁场dB的矢量和, 从而通过某一面元dS的总磁通量是各电流元产生元磁通的代数和。
至此,磁场的”高斯定理”得到了完全证明。