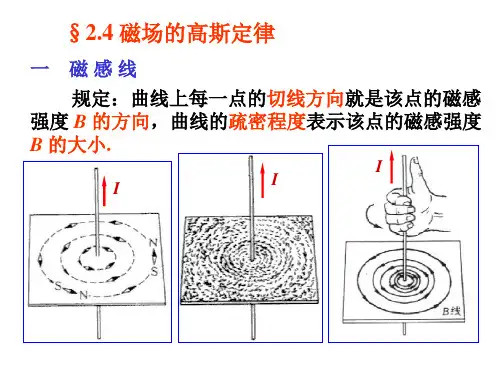
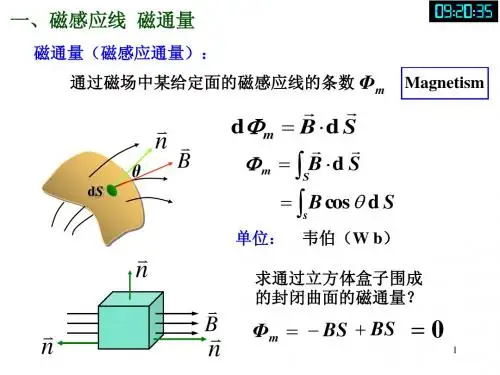
大学物理—磁通量 磁场中的高斯定理

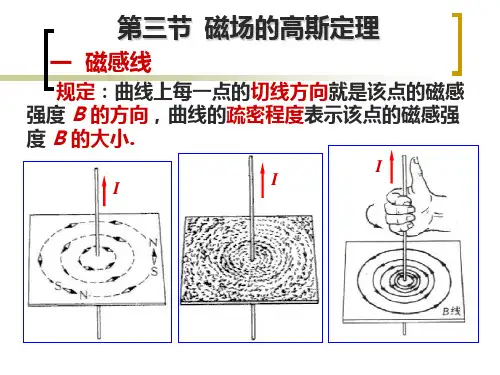
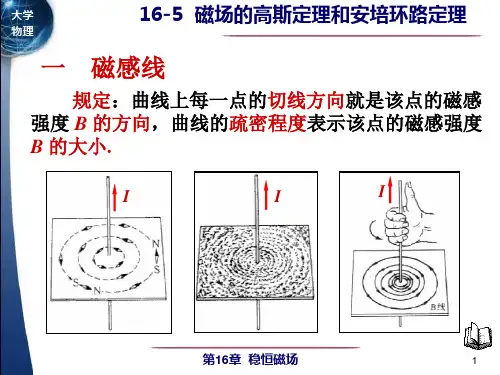
磁场中高斯定理公式(一)
磁场中高斯定理公式
什么是磁场中高斯定理公式？
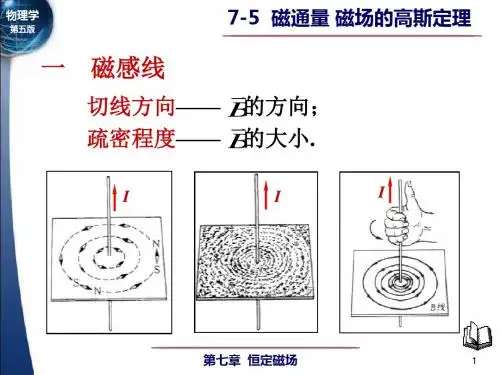
磁场中的高斯定理是电磁学中一个重要的定理，它描述了一个闭合曲面所围成的空间中的磁场总通量与该曲面上的磁场分布的关系。

根据磁场中的高斯定理公式，我们可以计算磁场通过一个封闭曲面的总磁通量。

高斯定理公式
高斯定理公式可以表示为：
∮B⋅dA=ΦB
其中， - $ $ 是磁感应强度（磁场向量）， - $ $ 是封闭曲面上的面积微元（法向量）， - $ _B $ 是磁场通过封闭曲面的总磁通量。

根据高斯定理，磁场通过一个封闭曲面的总磁通量等于磁场在该曲面上的散度。

示例解释
假设有一个半径为 $ R $ 的均匀磁场源，产生的磁感应强度为$ B $。

我们希望计算这个磁场通过一个半径为 $ r $ 的封闭曲面的总磁通量。

根据高斯定理公式，我们有：
∮B⋅dA=ΦB
根据对称性，磁场 $ $ 与面积微元 $ $ 的夹角为 0，因此上式可以简化为：
B⋅A=ΦB
其中， - $ A $ 是封闭曲面的面积。

由于磁场源是均匀的，磁感应强度 $ B $ 在封闭曲面上的每个面积微元 $ $ 上的取值都相同，因此可以提出来进行简化：
B⋅∫dA=ΦB
由于封闭曲面是一个圆柱体的侧表面，面积为 $ A = 2r L $，其中 $ L $ 是圆柱体的高度。

将这个表达式代入上式，可得：
B⋅2πrL=ΦB
总磁通量 $ _B $ 等于磁感应强度 $ B $ 乘以面积 $ 2r L $，即：
ΦB=2πrLB
这样，我们就计算出了磁场通过一个半径为 $ r $ 的封闭曲面的总磁通量。

磁高斯定理
磁高斯定理是一个重要的物理学理论，由哥本哈根大学的挪威物理学家，诺贝尔物理学家奥古斯特·磁高斯于1839年提出。

这个定理指出，任何给定的磁场，都可以由一个合适的磁向量场，即磁通量密度场来定义。

它表明，磁场是由磁向量场产生的，而不是由电荷分布引起的。

磁高斯定理的定义如下：对于任意闭合面S和其上的磁向量f，它们之间具有以下关系：
∫f•dl= ∫B•nds
其中f是内积，B是磁场，dl是封闭曲线的方向投影，nds是闭合面的法向量。

该定理的主要推论是，磁场的总流量，即数学上的积分，可以由已知的电荷分布来求得，而不必求出磁场本身。

这是一个非常重要的理论，因为它简化了对磁场的描述，而不必计算它的实际分布情况。

磁高斯定理表明，磁场是通过电流密度来描述的，而不是由电荷分布来描述。

这一定理最初是由磁高斯发现的，但是帕森斯在1860年重新分析并求得了该定理的希腊符号形式。

磁高斯定理在物理学，工程和其他应用领域有着广泛的应用，可以用来求出磁场的磁向量分布。

通过这种分布，我们可以知道磁场的方向和强度，从而估算磁场的复杂性。

此外，磁高斯定理在电力系统的设计以及磁学感测器的设计中也有重要的应用。