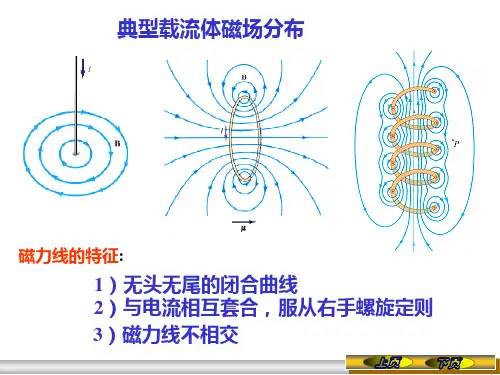
磁场-4 磁场中的高斯定理

磁场的高斯定理的物理意义
磁场的高斯定理的物理意义
磁场是指物体对磁性物质的影响，也就是电子、介子或离子在磁场中
运动时受到的作用力。

磁场的高斯定理是研究磁场的基本公式，主要
描述的是在空间某一点处，通过计算磁场的积分而可以得到磁场的大小。

这个定理是由德国数学家卡尔·费希尔于1835年发现的，他要解
决的是电流的分布，但他的结果也同样适用于磁场的研究。

磁场的高斯定理的基本物理意义就是，如果在空间某一点处做一个磁
场测量，那么就可以把这个空间分割成围绕这一点的若干虚拟的球体，并把它们的磁场值从内到外依此减小，如果可以计算出每个球体的磁
场值，那么就能用简单的数学公式计算出空间某一点处的磁场值，这
就是磁场的高斯定理。

磁场的高斯定理也可以用来解释磁场为什么会有一定的局部结构。

因
为它可以用来计算距离某一点的磁场强度，所以可以解释为什么磁场
会随着距离而减弱，以及为什么某个磁场中会有一些区域强度比较强，而其他区域强度比较弱。

此外，由于磁场的高斯定理可以计算出磁场的强度，因此它还可以用
来研究磁场的动态变化，比如某一磁体缩小后，周围磁场的变化，或
者磁体转动时，磁场的变化等。

因此，磁场的高斯定理也可以用来研
究磁场源和一些磁性物体间的相互作用，从而更好地理解磁场的性质。

总之，磁场的高斯定理的物理意义即可以用于计算空间某一点处的磁
场值，以及解释磁场的局部结构，还可以用来研究磁场的动态变化，以及磁场源和磁性物体的相互作用，从而更好地理解磁场的特征。

高斯磁场定理
高斯磁场定理是电磁学中的一个重要定理，也被称为安培定理或闭合回路定理。

该定理描述了一个闭合曲面内的磁场通量与该曲面所包围的电流的关系。

具体来说，高斯磁场定理表明，一个任意形状的闭合曲面所包围的磁场通量等于该曲面所包围的电流的代数和的某个常数倍。

这个常数倍就是磁场常数μ0，其值为约4π×10^-7
H/m。

高斯磁场定理的公式表达式为：∮B·dA = μ0·I，其中，∮B·dA表示对曲面S的
磁场通量积分，μ0表示磁场常数，I表示曲面S所包围的电流。

高斯磁场定理在电磁学中应用广泛，可以用于求解各种电磁场问题，如电磁感应、电磁波、电磁场强度等。

此外，高斯磁场定理还可以用于研究磁场的性质和规律，对于深入了解磁场的本质和特性具有重要意义。

总之，高斯磁场定理是电磁学中的一项基本定理，它描述了磁场通量与电流之间的关系，为解决各种电磁场问题提供了重要的理论工具。

什么是磁场中的高斯定理
在物理学中，磁场中的高斯定理是描述了闭合曲面内的磁场的总通量与该曲面内的电荷的数量之间的关系。

高斯定理的数学表达式为：
∮B · dA = μ₀ · ΣQ
其中，∮B · dA表示闭合曲面S内磁场的通量，B表示磁场的矢量，dA表示曲面元素，μ₀表示真空中的磁导率，ΣQ表示闭合曲面内的电荷总和。

换句话说，磁场中的高斯定理表明，磁场的总通量等于该闭合曲面内所有电荷的代数和。

这个定理可以帮助我们计算磁场的分布，并研究磁场与电荷之间的相互作用。

磁场的高斯定理摘要：首先推导出磁场的高斯定理，再由磁场的高斯定理和安培环路定理推导磁场在两种不同媒质分界面上必须满足的边界条件，最后由静电场与磁场的高斯定理比较引出关于磁单极子的问题。

1. 磁场的高斯定理在静电场中，高斯定理有01i SE S q ε⋅=∑⎰ ，所以静电场是有源场。

那么在磁场中，SB S ⋅⎰ 又得到什么呢？ 首先看一下磁感应强度B 。

B 的方向为磁力线的切线方向，大小为垂直B 的单位面积上穿过的磁力线的条数，即dN B dS ⊥=。

而通过面元的磁力线条数即为该面元的磁通量，于是m d B dS Φ=⋅ 。

对于有限曲面m B d S Φ=⋅⎰ ，对于闭合曲面m S B d S Φ=⋅⎰ 。

对于某一曲面，规定磁力线穿出为正，m Φ＞０；穿入为负，m Φ＜０。

而磁力线都是闭合的曲线，对于某一闭合的曲面，穿入到底总是等于穿出的，也就是说0m S B d S Φ=⋅=⎰ ，这就是磁场的高斯定理，也叫磁通连续性定理。

可以看出磁场是一个无源场。

2. 磁场的边界条件磁场的高斯定理（0S B d S ⋅=⎰ ）与安培环路定理（l H dl I ⋅=⎰ ）表征了恒定磁场的基本性质。

不论媒质分布情况如何，凡是恒定磁场，都具备这两个特性，它们称为恒定磁场的基本方程。

在两种不同媒质分界面上，围绕任一点Ｐ取一矩形回路，如右图，令20l ∆→，根据lH dl I ⋅=⎰ ，如果分界面上存在面自由电流，则有11211t t H l H l K l ∆-∆=∆即 12t t H H K -=根据B H μ= ，还可以写成1212t t B B K μμ-= 电流线密度Ｋ的正负要看它的方向与沿1t H 绕行方向是否符合右手螺旋关系而定。

写成矢量形式则为12()n H H e K -⨯= 。

其中n e 为分界面上从媒质１指向媒质２的法线方向单位矢量。

如果分界面上无电流，则12t t H H =说明在这种情况下磁场强度的切线分量是连续的，但磁感应强度切线分量是不连续的。

磁高斯定理
磁高斯定理，又称磁学高斯定理，是由德国物理学家卡尔·高斯于1839年提出的一个重要定理，也是磁学的定律。

它解释了由任意一个源点产生的磁场。

高斯定理表明，在满足一定条件的情况下，磁场密度在空间满足梯度为零的特殊条件。

高斯定理告诉我们，磁场总是从一个点源开始，或者从一个更大的波形延伸。

磁场的梯度无处不在，到达任何点都有一个方向，每个点的磁场强度都是相同的。

另外，高斯定理还说明，磁场的梯度为零; 也就是说，磁场的强度几乎是一样的，没有任何增加或减少的情况。

由于高斯定理是磁学的基础定律，因此它可用于解释和分析各种电磁及相关物理现象。

如以重力作用为例，高斯定理中的梯度等价于重力加速度；如以电流作用为例，高斯定理中的磁场对应于循环电流所产生的磁场；以气体流动为例，高斯定理中的梯度可用来描述流体力学中的涡流。

综上所述，磁高斯定理是物理学中一个重要的定理，它表明磁场的梯度总是为零，没有增加或减少的情况，并可以用来解释各种电磁及相关物理现象。

磁高斯定理
磁高斯定理（Maxwell's theorem）是磁力学的重要定理，由英国
物理学家乔治·马克斯韦（George Maxwell）于1865年提出。

它解释
了磁场的电流和旋转矢量之间的关系，是磁力学最根本的定律。

磁高斯定理可以用数学形式来表示：∇ × B = μ0J，其中B为
磁场，J为电流密度，μ0为真空磁导率（μ0=4π×10-7H/m），∇是
矢量求导运算符号。

这个定理描述了一个简单的物理现象：电流的旋
转产生了磁场，所以它是磁力学的基础。

磁高斯定理非常重要，可以解释各种电磁相关的现象。

它提供了
一种理解电磁学中电流向量、磁场强度和磁矢量之间关系的方法。

马
克斯韦在提出它的定理后，将电磁学理论推向了一个新的高度。

此外，磁高斯定理也可以用来解决电磁学中各种实际问题。

例如，它可以解释磁场强度的变化情况，从而帮助我们探索和分析电磁学现象。

总之，磁高斯定理是电磁学的基石，是磁力学的重要定理。

它不
仅能够精确地描述电磁学上的实际现象，而且可以结合其它电磁学定律，来求解一些复杂的实际问题。

磁场的高斯定理,说明高斯定律（gauss' law），属物理定律。

在静电场中，穿过任一封闭曲面的电场强度通量只与封闭曲面内的电荷的代数和有关，且等于封闭曲面的电荷的代数和除以真空中的电容率。

该定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。

静电场中通过任意闭合曲面（称高斯面）s 的电通量等于该闭合面内全部电荷的代数和除以真空中的电容率，与面外的电荷无关。

物理定律由于磁力线总是闭合曲线，因此任何一条进入一个闭合曲面的磁力线必定会从曲面内部出来，否则这条磁力线就不会闭合起来了。

如果对于一个闭合曲面，定义向外为正法线的指向，则进入曲面的磁通量为负，出来的磁通量为正，那么就可以得到通过一个闭合曲面的总磁通量为0。

这个规律类似于电场中的高斯定理，因此也称为高斯定理。

与静电场中的高斯定理相比较，两者有著本质上的区别。

在静电场中，由于自然界中存有着单一制的电荷，所以电场线存有起点和终点，只要闭合面内有净余的也已（或负）电荷，沿着闭合面的电通量就不等于零，即为静电场就是有源场；而在磁场中，由于自然界中没单独的磁极存有，n极和s极就是无法拆分的，磁感线都就是无头无尾的滑动线，所以通过任何闭合面的磁通量必等于零。

特别要强调两点： 1.关于电场线的方向的规定：电场线上每一点的切线方向就是该点电场的方向。

2.关于电场线的疏密的规定：电场线在某处的疏密要反映电场强度的大小，即在电场中通过某一点的电场线的数密度与该点电场强度的大小呈正相关，即： e=dn/ds，其中ds是在电场中的某一点取一个通过该点的且与电场线垂直的微分面，dn就是穿过该面ds的电场线的根数。

高斯定理来源于库仑定律,依赖场强共振原理,只有当电场线密度等同于场强悍小时场线通量就可以与场强通量等同于,并统一遵守高斯定理。

高斯面上的实际场强就是其内外所有电荷产生的场强共振而变成的合场强。

但利用高斯面所求出的场强则仅仅就是分析高斯面上场强原产时所牵涉的电荷在高斯面上产生的合场强,而不涵盖未牵涉的电荷所产生的场强。