数学：3.8《圆锥的侧面积》同步练习(鲁教版九年级上)

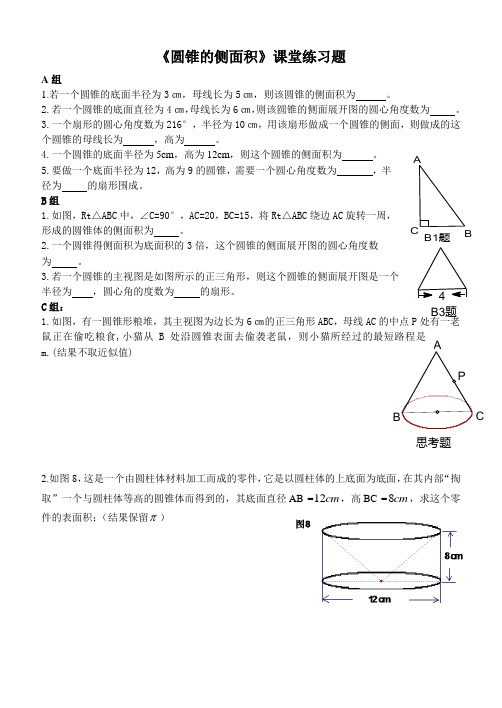
B3题B1题C BA 思考题C 《圆锥的侧面积》课堂练习题A 组1.若一个圆锥的底面半径为3㎝，母线长为5㎝，则该圆锥的侧面积为 。

2.若一个圆锥的底面直径为4㎝，母线长为6㎝，则该圆锥的侧面展开图的圆心角度数为 。

3.一个扇形的圆心角度数为216°，半径为10㎝，用该扇形做成一个圆锥的侧面，则做成的这个圆锥的母线长为 ，高为 。

4.一个圆锥的底面半径为5cm ，高为12cm ，则这个圆锥的侧面积为 。

5.要做一个底面半径为12，高为9的圆锥，需要一个圆心角度数为 ，半径为 的扇形围成。

B 组1.如图，Rt △ABC 中，∠C=90°，AC=20，BC=15，将Rt △ABC 绕边AC 旋转一周，形成的圆锥体的侧面积为 。

2.一个圆锥得侧面积为底面积的3倍，这个圆锥的侧面展开图的圆心角度数为 。

3.若一个圆锥的主视图是如图所示的正三角形，则这个圆锥的侧面展开图是一个 半径为 ，圆心角的度数为 的扇形。

C 组：1.如图，有一圆锥形粮堆，其主视图为边长为6㎝的正三角形ABC ，母线AC 的中点P 处有一老鼠正在偷吃粮食,小猫从B 处沿圆锥表面去偷袭老鼠，则小猫所经过的最短路程是m.(结果不取近似值)2.如图8，这是一个由圆柱体材料加工而成的零件，它是以圆柱体的上底面为底面，在其内部“掏取”一个与圆柱体等高的圆锥体而得到的，其底面直径AB =cm 12，高BC =cm 8，求这个零件的表面积；（结果保留 ）5题6题7题图2《圆锥的侧面积》练习题1.某圆锥体的底面直径为4㎝，高为√21㎝，这个圆锥的侧面积为 ，他的侧面展开图是一个半径为 ，圆心角度数为 的扇形。

2.一个扇形的圆心角为216°，半径为15㎝，用这样的扇形围成一个圆锥的侧面，需要一个半径为 的圆作底面，这个圆锥的高为 。

3.某圆锥的侧面展开图的面积为15π㎝2，母线长为5㎝，则该圆锥的底面直径为 。

4.一个圆锥体的侧面展开图是一个半圆，底面积为15π5.如图，已知圆锥的底面半径OA=4cm ，母线SA=12cm,⑴一只蚂蚁从A 处出发绕侧面一周(回到原来的位置)的最短距离为 。

第二章 2.8 圆锥的侧面积一．选择题（共10小题）1．（2019•遵义）圆锥的底面半径是5cm，侧面展开图的圆心角是180°，圆锥的高是（）A．5cm B．10cm C．6cm D．5cm 2．（2019•云南）一个圆锥的侧面展开图是半径为8的半圆，则该圆锥的全面积是（）A．48πB．45πC．36πD．32π3．（2019•西藏）如图，从一张腰长为90cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的底面半径为（）A．15cm B．12cm C．10cm D．20cm 4．（2019•荆州）如图，点C为扇形OAB的半径OB上一点，将△OAC沿AC折叠，点O恰好落在上的点D处，且l：l＝1：3（l表示的长），若将此扇形OAB围成一个圆锥，则圆锥的底面半径与母线长的比为（）A．1：3B．1：πC．1：4D．2：9 5．（2019•巴中）如图，圆锥的底面半径r＝6，高h＝8，则圆锥的侧面积是（）A．15πB．30πC．45πD．60π6．（2019•宁波）如图所示，矩形纸片ABCD中，AD＝6cm，把它分割成正方形纸片ABFE 和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则AB的长为（）A．3.5cm B．4cm C．4.5cm D．5cm 7．（2019•金华）如图物体由两个圆锥组成．其主视图中，∠A＝90°，∠ABC＝105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为（）A．2B．C．D．8．（2018•鄂尔多斯）如图，从一块直径为2的圆形铁皮上剪出一个圆心角为90°的扇形CAB，且点C，A，B都在⊙O上，将此扇形围成一个圆锥，则该圆锥底面圆的半径是（）A．B．C．D．9．如图，从一块半径为2m的圆形铁皮上剪出一个半径为2m的扇形，则此扇形围成的圆锥的侧面积为（）A．2πm2B．C．πm2D．10．如图，如果从半径为9cm的圆形纸片剪去圆周的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的底面半径为（）A．6cm B．3cm C．5cm D．3cm二．填空题（共9小题）11．（2019•鸡西）若一个圆锥的底面圆的周长是5πcm，母线长是6cm，则该圆锥的侧面展开图的圆心角度数是．12．（2019•绥化）用一个圆心角为120°的扇形作一个圆锥的侧面，若这个圆锥的底面半径恰好等于4，则这个圆锥的母线长为．13．（2019•贵港）如图，在扇形OAB中，半径OA与OB的夹角为120°，点A与点B的距离为2，若扇形OAB恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为．14．（2019•淮安）若圆锥的侧面积是15π，母线长是5，则该圆锥底面圆的半径是．15．（2019•安顺）如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径r＝2，扇形的圆心角θ＝120°，则该圆锥母线l的长为．16．（2019•杭州）如图是一个圆锥形冰淇淋外壳（不计厚度），已知其母线长为12cm，底面圆半径为3cm，则这个冰淇淋外壳的侧面积等于cm2（结果精确到个位）．17．如图，若从一块半径是6cm的圆形纸片圆O上剪出一个圆心角为60°的扇形（点A、B、C在圆O上），再将剪下的扇形围成一个圆锥，则该圆锥的底面圆半径是cm．18．一圆锥的母线长为3，底面半径为1，则该圆锥的侧面积为．19．如图，圆锥侧面展开得到扇形，此扇形半径CA＝9，圆心角∠ACB＝120°，则此圆锥高的OC的长度是．三．解答题（共7小题）20．小明同学用纸板制作了一个圆锥形漏斗模型，如图所示，它的底面半径OB＝3cm，高OC＝4cm，求这个圆锥形漏斗的侧面积．21．一个圆锥的侧面展开图是半径为8cm，圆心角为120°的扇形，求：（1）圆锥的底面半径；（2）圆锥的全面积．22．在数学活动课中，同学们准备了一些等腰直角三角形纸片，从每张纸片中剪出一个扇形制作圆锥玩具模型．如图，已知△ABC是腰长为16cm的等腰直角三角形．（1）在等腰直角三角形ABC纸片中，以C为圆心，剪出一个面积最大的扇形（要求：尺规作图，保留作图痕迹，不写作法）；（2）请求出所制作圆锥底面的半径长．23．如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连接EO、FO，若DE＝4，∠DP A＝45°（1）求⊙O的半径．（2）若图中扇形OEF围成一个圆锥侧面，试求这个圆锥的底面圆的半径．24．如图，将弧长为6π，圆心角为120°的扇形纸片AOB围成圆锥形纸帽，使扇形的两条半径OA与OB重合（接缝粘连部分忽略不计），求圆锥形纸帽的高．25．有一个直径为1m的圆形铁皮，要从中剪出一个最大的圆心角为90°的扇形ABC，如图所示．（1）求被剪掉阴影部分的面积：（2）用所留的扇形铁皮围成一个圆锥，该圆锥的底面圆的半径是多少？26．如图，在梯形ABCD中，AD∥BC，∠C＝90°，∠BAD＝120°，AB＝AD＝4，BC＝6，以点A为圆心在这个梯形内画出一个最大的扇形（图中阴影部分）．（1）求这个扇形的面积；（2）若将这个扇形围成圆锥，求这个圆锥的底面积．答案与解析一．选择题（共10小题）1．（2019•遵义）圆锥的底面半径是5cm，侧面展开图的圆心角是180°，圆锥的高是（）A．5cm B．10cm C．6cm D．5cm【分析】设圆锥的母线长为R，根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到2π•5＝，然后解方程即可母线长，然后利用勾股定理求得圆锥的高即可．【解答】解：设圆锥的母线长为R，根据题意得2π•5＝，解得R＝10．即圆锥的母线长为10cm，∴圆锥的高为：＝5cm．故选：A．【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．2．（2019•云南）一个圆锥的侧面展开图是半径为8的半圆，则该圆锥的全面积是（）A．48πB．45πC．36πD．32π【分析】首先利用圆的面积公式即可求得侧面积，利用弧长公式求得圆锥的底面半径，得到底面面积，据此即可求得圆锥的全面积．【解答】解：侧面积是：πr2＝×π×82＝32π，底面圆半径为：，底面积＝π×42＝16π，故圆锥的全面积是：32π+16π＝48π．故选：A．【点评】本题考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．3．（2019•西藏）如图，从一张腰长为90cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的底面半径为（）A．15cm B．12cm C．10cm D．20cm【分析】根据等腰三角形的性质得到OE的长，再利用弧长公式计算出弧CD的长，设圆锥的底面圆的半径为r，根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长得到r，然后利用勾股定理计算出圆锥的高．【解答】解：过O作OE⊥AB于E，∵OA＝OB＝90cm，∠AOB＝120°，∴∠A＝∠B＝30°，∴OE＝OA＝45cm，∴弧CD的长＝＝30π，设圆锥的底面圆的半径为r，则2πr＝30π，解得r＝15．故选：A．【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．4．（2019•荆州）如图，点C为扇形OAB的半径OB上一点，将△OAC沿AC折叠，点O 恰好落在上的点D处，且l：l＝1：3（l表示的长），若将此扇形OAB围成一个圆锥，则圆锥的底面半径与母线长的比为（）A．1：3B．1：πC．1：4D．2：9【分析】连接OD，能得∠AOB的度数，再利用弧长公式和圆的周长公式可求解．【解答】解：连接OD交OC于M．由折叠的知识可得：OM＝OA，∠OMA＝90°，∴∠OAM＝30°，∴∠AOM＝60°，∵且：＝1：3，∴∠AOB＝80°设圆锥的底面半径为r，母线长为l，＝2πr，∴r：i＝2：9．故选：D．【点评】本题运用了弧长公式和轴对称的性质，关键是运用了转化的数学思想．5．（2019•巴中）如图，圆锥的底面半径r＝6，高h＝8，则圆锥的侧面积是（）A．15πB．30πC．45πD．60π【分析】圆锥的侧面积：S侧＝•2πr•l＝πrl，求出圆锥的母线l即可解决问题．【解答】解：圆锥的母线l＝＝＝10，∴圆锥的侧面积＝π•10•6＝60π，故选：D．【点评】本题考查圆锥的侧面积，勾股定理等知识，解题的关键是记住圆锥的圆锥的侧面积公式．6．（2019•宁波）如图所示，矩形纸片ABCD中，AD＝6cm，把它分割成正方形纸片ABFE 和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则AB的长为（）A．3.5cm B．4cm C．4.5cm D．5cm【分析】设AB＝xcm，则DE＝（6﹣x）cm，根据扇形的弧长等于圆锥底面圆的周长列出方程，求解即可．【解答】解：设AB＝xcm，则DE＝（6﹣x）cm，根据题意，得＝π（6﹣x），解得x＝4．故选：B．【点评】本题考查了圆锥的计算，矩形的性质，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．7．（2019•金华）如图物体由两个圆锥组成．其主视图中，∠A＝90°，∠ABC＝105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为（）A．2B．C．D．【分析】先证明△ABD为等腰直角三角形得到∠ABD＝45°，BD＝AB，再证明△CBD 为等边三角形得到BC＝BD＝AB，利用圆锥的侧面积的计算方法得到上面圆锥的侧面积与下面圆锥的侧面积的比等于AB：CB，从而得到下面圆锥的侧面积．【解答】解：∵∠A＝90°，AB＝AD，∴△ABD为等腰直角三角形，∴∠ABD＝45°，BD＝AB，∵∠ABC＝105°，∴∠CBD＝60°，而CB＝CD，∴△CBD为等边三角形，∴BC＝BD＝AB，∵上面圆锥与下面圆锥的底面相同，∴上面圆锥的侧面积与下面圆锥的侧面积的比等于AB：CB，∴下面圆锥的侧面积＝×1＝．故选：D．【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．也考查了等腰直角三角形和等边三角形的性质．8．（2018•鄂尔多斯）如图，从一块直径为2的圆形铁皮上剪出一个圆心角为90°的扇形CAB，且点C，A，B都在⊙O上，将此扇形围成一个圆锥，则该圆锥底面圆的半径是（）A．B．C．D．【分析】连接BC，如图，利用圆周角定理得到BC为⊙O的直径，则AB＝AC＝，设该圆锥底面圆的半径为r，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr＝，然后解方程即可．【解答】解：连接BC，如图，∵∠BAC＝90°，∴BC为⊙O的直径，BC＝2，∴AB＝AC＝，设该圆锥底面圆的半径为r，∴2πr＝，解得r＝，即该圆锥底面圆的半径为．故选：D．【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．也考查了圆周角定理．9．（2019•张店区一模）如图，从一块半径为2m的圆形铁皮上剪出一个半径为2m的扇形，则此扇形围成的圆锥的侧面积为（）A．2πm2B．C．πm2D．【分析】根据题意求得扇形的圆心角的度数，然后利用扇形面积公式求解即可．【解答】解：如图：连接OA，OB，作OD⊥AB于点D，由题意知：AB＝2，OA＝OB＝2，所以AD＝，∴∠BAO＝30°，∴∠BAC＝60°，∴扇形面积为：＝2π，故选：A．【点评】本题考查了圆锥的计算，解题的关键是求得扇形的圆心角，难度不大．10．（2018秋•临洮县期末）如图，如果从半径为9cm的圆形纸片剪去圆周的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的底面半径为（）A．6cm B．3cm C．5cm D．3cm【分析】设圆锥的底面圆半径为r，先利用圆的周长公式计算出剩下的扇形的弧长，然后把它作为圆锥的底面圆的周长进行计算即可．【解答】解：设圆锥的底面圆半径为r，∵半径为9cm的圆形纸片剪去一个圆周的扇形，∴剩下的扇形的弧长＝•2π•9＝12π，∴2π•r＝12π，∴r＝6．故选：A．【点评】本题考查了圆锥的有关计算：圆锥的侧面展开图为扇形，圆锥的底面圆的周长等于扇形的弧长．也考查了圆的周长公式．二．填空题（共9小题）11．（2019•鸡西）若一个圆锥的底面圆的周长是5πcm，母线长是6cm，则该圆锥的侧面展开图的圆心角度数是150°．【分析】利用圆锥的底面周长和母线长求得圆锥的侧面积，然后再利用圆锥的面积的计算方法求得侧面展开扇形的圆心角的度数即可．【解答】解：∵圆锥的底面圆的周长是45cm，∴圆锥的侧面扇形的弧长为5πcm，∴＝5π，解得：n＝150故答案为150°．【点评】本题考查了圆锥的计算，解题的关键是根据圆锥的侧面展开扇形的弧长等于圆锥的底面周长来求出弧长．12．（2019•绥化）用一个圆心角为120°的扇形作一个圆锥的侧面，若这个圆锥的底面半径恰好等于4，则这个圆锥的母线长为12．【分析】根据底面周长等于圆锥的侧面展开扇形的弧长列式计算即可．【解答】解：设圆锥的母线长为l，根据题意得：＝2π×4，解得：l＝12，故答案为：12．【点评】考查了扇形的弧长公式；圆的周长公式；用到的知识点为：圆锥的弧长等于底面周长．13．（2019•贵港）如图，在扇形OAB中，半径OA与OB的夹角为120°，点A与点B的距离为2，若扇形OAB恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为．【分析】利用弧长＝圆锥的底面周长这一等量关系可求解．【解答】解：连接AB，过O作OM⊥AB于M，∵∠AOB＝120°，OA＝OB，∴∠BAO＝30°，AM＝，∴OA＝2，∵＝2πr，∴r＝故答案是：【点评】本题运用了弧长公式和圆的周长公式，建立准确的等量关系是解题的关键．14．（2019•淮安）若圆锥的侧面积是15π，母线长是5，则该圆锥底面圆的半径是3．【分析】设该圆锥底面圆的半径是为r，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形面积公式得到×2π×r×5＝15π，然后解关于r的方程即可．【解答】解：设该圆锥底面圆的半径是为r，根据题意得×2π×r×5＝15π，解得r＝3．即该圆锥底面圆的半径是3．故答案为3．【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．15．（2019•安顺）如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径r＝2，扇形的圆心角θ＝120°，则该圆锥母线l的长为6．【分析】利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到2π×2＝，然后解关于l的方程即可．【解答】解：根据题意得2π×2＝，解德l＝6，即该圆锥母线l的长为6．故答案为6．【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．16．（2019•杭州）如图是一个圆锥形冰淇淋外壳（不计厚度），已知其母线长为12cm，底面圆半径为3cm，则这个冰淇淋外壳的侧面积等于113cm2（结果精确到个位）．【分析】利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式计算．【解答】解：这个冰淇淋外壳的侧面积＝×2π×3×12＝36π≈113（cm2）．故答案为113．【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．17．如图，若从一块半径是6cm的圆形纸片圆O上剪出一个圆心角为60°的扇形（点A、B、C在圆O上），再将剪下的扇形围成一个圆锥，则该圆锥的底面圆半径是cm．【分析】连接OA，作OD⊥AB于点D，利用三角函数即可求得AD的长，则AB的长可以求得，然后利用弧长公式即可求得弧长，即底面圆的周长，再利用圆的周长公式即可【解答】解：连接OA，作OD⊥AB于点D．在直角△OAD中，OA＝6，∠OAD＝∠BAC＝30°，则AD＝OA•cos30°＝3．则AB＝2AD＝6，则扇形的弧长是：＝2π，设底面圆的半径是r，则2π×1＝2π，解得：r＝．故答案为：．【点评】本题考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．18．一圆锥的母线长为3，底面半径为1，则该圆锥的侧面积为3π．【分析】圆锥的侧面积＝π×底面半径×母线长；【解答】解：圆锥的侧面积＝π×3×1＝3π；故答案为：3π．【点评】考查圆锥的侧面积公式，掌握相应公式是关键．19．如图，圆锥侧面展开得到扇形，此扇形半径CA＝9，圆心角∠ACB＝120°，则此圆锥高的OC的长度是6．【分析】设这个圆锥的底面半径为r，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到2πr＝，解方程求出r，然后利用勾股定理计算出OC．【解答】解：设这个圆锥的底面半径为r，根据题意得2πr＝，所以OC＝＝＝6．答：此圆锥高的OC的长度为6．故答案为6．【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．三．解答题（共7小题）20．小明同学用纸板制作了一个圆锥形漏斗模型，如图所示，它的底面半径OB＝3cm，高OC＝4cm，求这个圆锥形漏斗的侧面积．【分析】首先根据底面半径OB＝3cm，高OC＝4cm，求出圆锥的母线长，再利用圆锥的侧面积公式求出即可．【解答】解：根据题意，由勾股定理可知BC2＝BO2+CO2．∴BC＝5cm，∴圆锥形漏斗的侧面积＝π•OB•BC＝15πcm2．，【点评】此题主要考查了圆锥的侧面积公式求法，正确的记忆圆锥侧面积公式是解决问题的关键．21．一个圆锥的侧面展开图是半径为8cm，圆心角为120°的扇形，求：（1）圆锥的底面半径；（2）圆锥的全面积．【分析】（1）根据弧长公式求出底面周长，根据圆的周长公式计算即可；（2）根据扇形面积公式和圆的面积公式计算．【解答】解：（1）设圆锥的底面半径为rcm，扇形的弧长＝＝，∴2πr＝，解得，r＝，即圆锥的底面半径为cm；（2）圆锥的全面积＝+π×（）2＝cm2．【点评】本题考查的是圆锥的计算，圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．22．在数学活动课中，同学们准备了一些等腰直角三角形纸片，从每张纸片中剪出一个扇形制作圆锥玩具模型．如图，已知△ABC是腰长为16cm的等腰直角三角形．（1）在等腰直角三角形ABC纸片中，以C为圆心，剪出一个面积最大的扇形（要求：尺规作图，保留作图痕迹，不写作法）；（2）请求出所制作圆锥底面的半径长．【分析】（1）根据题意作出图形即可；（2）根据勾股定理得到AB＝16，由（1）可知CD平分∠ACB，根据等腰三角形的性质得到CD⊥AB，根据弧长的公式即可得到结论．【解答】解：（1）如图所示：扇形CEF为所求作的图形；（2）∵△ABC是等腰直角三角形，且AC＝BC＝16cm，∴AB＝16cm，由（1）可知CD平分∠ACB，∴CD⊥AB，∴CD＝8cm，设圆锥底面的半径长为r，依题意得：2πr＝，∴r＝2cm，答：所制作圆锥底面的半径长为2cm．【点评】本题考查了作图﹣应用与设计作图，等腰直角三角形的性质，弧长的计算，正确的作出图形是解题的关键．23．如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连接EO、FO，若DE＝4，∠DP A＝45°（1）求⊙O的半径．（2）若图中扇形OEF围成一个圆锥侧面，试求这个圆锥的底面圆的半径．【分析】（1）利用垂径定理得到CE＝DC＝DE＝2，OC＝OE，则∠OEC＝30°，然后利用含30度的直角三角形三边的关系求出OE即可；（2）利用圆周角定理得到∠EOF＝2∠D＝90°，设这个圆锥的底面圆的半径为r，利用弧长公式得到2πr＝，然后解关于r的方程即可．【解答】解：（1）∵弦DE垂直平分半径OA，∴CE＝DC＝DE＝2，OC＝OE，∴∠OEC＝30°，∴OC＝＝2，∴OE＝2OC＝4，即⊙O的半径为4；（2）∵∠DP A＝45°，∴∠D＝45°，∴∠EOF＝2∠D＝90°，设这个圆锥的底面圆的半径为r，∴2πr＝，解得r＝1，即这个圆锥的底面圆的半径为1．【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．也考查了垂径定理和圆周角定理．24．如图，将弧长为6π，圆心角为120°的扇形纸片AOB围成圆锥形纸帽，使扇形的两条半径OA与OB重合（接缝粘连部分忽略不计），求圆锥形纸帽的高．【分析】设圆锥的底面圆的半径为r，利用这个扇形的弧长等于圆锥底面的周长得到2πr＝6π，解得r＝3，设扇形AOB的半径为R，根据弧长公式得到＝6π，解得R＝9，然后根据勾股定理计算圆锥形纸帽的高．【解答】解：设圆锥的底面圆的半径为r，则2πr＝6π，解得r＝3，设扇形AOB的半径为R，则＝6π，解得R＝9，所以圆锥形纸帽的高＝＝6．【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．25．有一个直径为1m的圆形铁皮，要从中剪出一个最大的圆心角为90°的扇形ABC，如图所示．（1）求被剪掉阴影部分的面积：（2）用所留的扇形铁皮围成一个圆锥，该圆锥的底面圆的半径是多少？【分析】（1）由∠BAC＝90°，得BC为⊙O的直径，即BC＝1m；又由AB＝AC，得到AB＝BC＝，而S阴影部分＝S⊙O﹣S扇形ABC，然后根据扇形和圆的面积公式进行计算即可；（2）扇形的半径是AB＝，扇形BAC的弧长l＝＝π，圆锥的底面周长等于侧面展开图的扇形弧长，然后利用弧长公式计算．【解答】解：（1）如图，连接BC，∵∠BAC＝90°，∴BC为⊙O的直径，即BC＝1m，又∵AB＝AC，∴．∴（平方米）（2）设底面圆的半径为r，则，∴．圆锥的底面圆的半径长为米．【点评】本题考查了扇形的面积公式：S＝，其中n为扇形的圆心角的度数，R 为圆的半径），或S＝lR，l为扇形的弧长，R为半径．也考查了90度的圆周角所对的弦为直径以及等腰直角三角形三边关系．26．如图，在梯形ABCD中，AD∥BC，∠C＝90°，∠BAD＝120°，AB＝AD＝4，BC＝6，以点A为圆心在这个梯形内画出一个最大的扇形（图中阴影部分）．（1）求这个扇形的面积；（2）若将这个扇形围成圆锥，求这个圆锥的底面积．【分析】（1）作AE⊥BC，根据三角函数求得扇形的半径AE，由梯形的性质得出圆心角度数，继而根据扇形的面积公式可得．（2）根据圆锥的底面周长等于扇形的弧长，从而求得底面半径，从而求得面积．【解答】解：（1）过点A作AE⊥BC于E，则AE＝AB sin B＝4×＝2，∵AD∥BC，∠BAD＝120°，∴扇形的面积为＝4π，（2）设圆锥的底面半径为r，则2πr＝，解得：r＝若将这个扇形围成圆锥，这个圆锥的底面积π．【点评】本题要熟知切线的性质，直角梯形的性质和扇形弧长计算公式．利用切线的性质求得AE的长即半径是解题的关键，注意扇形的周长为两条半径的长加上弧长．。

2.8圆锥的侧面积同步练习苏科版九年级数学上册（含答案）2.8 圆锥的侧面积一、选择题1.圆锥的底面半径是5 cm,侧面展开图的圆心角是180°,圆锥的高是() A.53 cm B.10 cm C.6 cm D.5 cm 2.如图1,在正方形网格中,扇形OAB是圆锥的侧面展开图,∠AOB=90°,若每个小正方形的边长均为1厘米,则这个圆锥的底面圆半径为() 图 1 A.12厘米 B.22厘米 C.2厘米D.22厘米3.[2020·湖北] 一个圆锥的底面圆半径是4 cm,其侧面展开图的圆心角是120°,则圆锥的母线长是() A.8 cm B.12 cm C.16 cm D.24 cm4.[2020·青海] 如图2是一个废弃的扇形统计图,小明同学利用它的阴影部分制作一个圆锥,则这个圆锥的底面圆半径是() 图2 A.3.6 B.1.8 C.3 D.65.如图3,要制作一顶圆锥形的烟囱帽,使底面圆的半径与母线长的比是4∶5,那么所需扇形铁皮的圆心角应为() 图3 A.288° B.216° C.144° D.120°6.如图4,蒙古包可近似地看作由圆锥和圆柱组成,若用毛毡搭建一个底面圆面积为25π m2,圆柱高为3 m,圆锥高为2 m的蒙古包,则需要毛毡的面积是() 图4 A.(30+529)π m2 B.40π m2 C.(30+521)π m2 D.55π m27.[2019·宁波] 如图5所示,矩形纸片ABCD中,AD=6 cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为() 图5 A.3.5 cm B.4 cm C.4.5 cm D.5 cm8.[2019·荆州] 如图6,C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在AB上的点D处,且BDl∶ADl=1∶3(BDl表示BD的长),若将此扇形OAB围成一个圆锥,则圆锥的底面圆半径与母线长的比为() 图 6 A.1∶3 B.1∶π C.1∶4 D.2∶9 二、填空题9.[2020·宿迁] 用半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆的半径为. 10.[2019·徐州] 如图7,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆半径r=2 cm,扇形的圆心角θ=120°,则该圆锥的母线长l为cm. 图7 11.[2020·徐州] 如图8,在Rt△ABC中,∠C=90°,AC=4,BC=3.若以AC所在直线为轴,把△ABC旋转一周,得到一个圆锥,则这个圆锥的侧面积等于. 图8 12.如图9,现有一张圆心角为108°,半径为40 cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面圆半径为10 cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ为. 图9 三、解答题13.已知扇形的圆心角为120°,面积为300π cm2. (1)求扇形的弧长; (2)如果把这个扇形卷成一个圆锥,那么圆锥的高是多少? 14.[2019·启东期末] 如图10,一个圆锥形工艺品,它的高为33 cm,侧面展开图是半圆.求: (1)圆锥的母线长与底面圆半径之比; (2)圆锥的侧面积. 图10 15.[2019·扬州广陵区期末] 如图11所示,已知圆锥的底面圆半径r=10 cm,母线长为40 cm. (1)求它的侧面展开图的圆心角和表面积; (2)若一甲虫从A点出发沿着圆锥侧面爬行到母线SA的中点B处,请你动脑筋想一想,它所走的最短路线长是多少. 图11 16. 如图12,正三角形ABC的边长为1 cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3绕点A 顺时针旋转120°至AP4,形成扇形D4……设ln为扇形Dn的弧长(n=1,2,3,…),回答下列问题: (1)按要求填表: n 1 2 3 4 ln(cm) (2)根据上表,试估计n至少为何值时,扇形Dn的弧长能绕地球赤道一周?(设地球赤道的半径为6400 km) (3)圆锥的侧面积实际上是侧面展开图的.若已知圆锥侧面展开图的圆心角为n°和半径R,则它的侧面积是;若已知圆锥的母线长l和底面圆半径r,则它的侧面积是. 图12 答案 1.[解析] A设圆锥的母线长为R.根据题意,得2π·5=180πR180,解得R=10.即圆锥的母线长为10 cm,∴圆锥的高为102-52=53(cm).故选 A.2.[解析] B扇形的半径为22+22=22(厘米),∴扇形的弧长为90π×*****=2π(厘米),∴这个圆锥的底面圆半径为2π÷2π=22(厘米).故选B.3.[解析] B设圆锥的母线长为R cm. ∵圆锥的底面圆周长为2π×4=8π(cm), ∴120×π×R180=8π, 解得R=12,即圆锥的母线长为12 cm.故选B.4.[解析] A设这个圆锥的底面圆半径为r. 根据题意,得2πr=(360-252)×π×*****. 解得r=3.6, 即这个圆锥的底面圆半径是3.6.故选A.5.[解析] A∵底面圆的半径与母线长的比是4∶5, ∴设底面圆的半径为4x,则母线长是5x,扇形铁皮的圆心角为n°, 则2π×4x=nπ×5x180,解得n=288.故选A.6.[解析] A设底面圆的半径为R m,则πR2=25π,解得R=5,则圆锥的母线长为22+52=29(m),所以圆锥的侧面积为12×2π×5×29=529π(m2),圆柱的侧面积为2π×5×3=30π(m2),所以需要毛毡的面积为(30π+529π)m2.故选A.7.[解析] B设AB=x cm,则DE=(6-x)cm. 根据题意,得90πx180=π(6-x),解得x=4. 故选B.8.[解析] D连接OD交AC于点M. 由折叠的性质可得OA=AD, 又OD=OA, ∴OA=AD=OD,∴∠AOM=60°. ∵BDl∶ADl=1∶3,∴∠AOB=80°. 设圆锥的底面圆半径为r,母线长为l,则80πl180=2πr,∴r∶l=2∶9.故选D. 9.[答案] 1 [解析] 设这个圆锥的底面圆的半径为r.根据题意,得2πr=90·π·4180, 解得r=1,所以这个圆锥的底面圆的半径为1. 10.[答案] 6 [解析] 圆锥的底面圆周长=2π×2=4π(cm). 设圆锥的母线长为R cm,则120π×R180=4π,解得R=6.故答案为6. 11.[答案] 15π [解析] 由已知,得母线长为5, ∴圆锥的侧面积是πrl=5×3×π=15π.故答案为15π. 12.[答案] 18° [解析] 设剩下扇形纸片的圆心角为n°,则2π×10=nπ×*****,解得n=90.∵扇形纸片的圆心角是108°,∴剪去的扇形纸片的圆心角为108°-90°=18°. 13.解:(1)设扇形的半径为R(R0) cm. 根据题意,得300π=120·π·R2360,解得R=30, 所以扇形的弧长为120×π×*****=20π(cm). (2)设圆锥底面圆的半径为r cm. 根据题意,得2πr=20π,解得r=10, 所以圆锥的高是302-102=202(cm). 14.解:设圆锥底面圆半径为r cm,母线长为l cm.(1)由题意知2πr=πl,∴l∶r=2∶1. 答:圆锥的母线长与底面圆半径之比为2∶1. (2)由题意知r2+(33)2=l2. 把l=2r代入,解得r1=-3(舍去),r2=3, ∴l=6,∴圆锥的侧面积为πrl=18π(cm2). 15.解:(1)设圆锥的侧面展开图的圆心角为n°.nπ×*****=2π×10,解得n=90,故它的侧面展开图的圆心角为90°. 圆锥的表面积为π×102+π×10×40=500π(cm2). (2)如图,由圆锥的侧面展开图可知,甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路线长是线段AB的长. 在Rt△ASB中,SA=40 cm,SB=20 cm, ∴AB=205 cm. ∴甲虫所走的最短路线长是205 cm. 12.解:(1)根据弧长公式,得l1=120π×1180=2π3(cm); l2=120π×2180=4π3(cm); l3=120π×3180=2π(cm); l4=120π×4180=8π3(cm). 故填表如下: n 1 2 3 4 ln(cm) 2π3 4π3 2π 8π3 (2)根据上述规律可知:ln=120π×n180=2π×6400×105,解得n=1.92×109. (3)面积nπR2360πrl。

随堂测试2.8圆锥的侧面积1．将一个圆锥展开后，其侧面是一个圆心角为108°，半径为12cm的扇形，则该圆锥的底面半径是（）A．1.8cm B．3.6cm C．4cm D．6cm2．一个圆锥的底面半径为1cm，侧面积为4πcm2，现将其侧面展开平铺成的扇形的圆心角为（）A．90°B．135°C．60°D．45°3．圆锥的高是4cm，其底面圆半径为3cm，则它的侧面展开图的面积为（）A．12πcm2B．24πcm2C．15πcm2D．30πcm24．圆锥的截面是一个等边三角形，则它的侧面展开图扇形的圆心角度数是（）A．60°B．90°C．120°D．180°5．一个圆锥的侧面展开图是一个面积为的半圆，则该圆锥的高为（）A．.1B．2C．D．6．一个圆柱的侧面展开正好是一个正方形，这个圆柱的底面直径与高的比是（）A．1：πB．π：1C．1：2πD．2π：17．若圆锥的底面半径为2cm，侧面展开图的面积为2πcm2，则圆锥的母线长为（）A．1cm B．2cm C．3cm D．cm8．一个圆锥的侧面展开图是一个半圆，则圆锥的母线与底面半径所成角的度数是（）A．15°B．30°C．45°D．60°9．一个圆锥的轴截面是一个边长为2的等边三角形，则它的侧面积是（）A．πB．2πC．2πD．4π10．如图，从一块直径是2的圆形铁片上剪出一个圆心角为90°的扇形，将剪下来的扇形围成一个圆锥．那么这个圆锥的底面圆的半径是（）A．B．C．D．111．如图，已知扇形OAB的半径为6cm，圆心角的度数为120°，若将OA，OB重合后围成一圆锥侧面，那么圆锥的底面半径为（）A．2cm B．3cm C．6cm D．2cm12．如图，圆锥底面半径为r，母线长为20cm，其侧面展开图是圆心角为216°的扇形，则r的值为（）A．12cm B．15cm C．4πcm D．5πcm13．用半径为50，圆心角为120°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面半径为．14．若一个圆锥的底面半径为1cm，它的侧面展开图的圆心角为90°，则这个圆锥的母线长为cm．15．设圆锥的底面半径为2，母线长为3，该圆锥的侧面积为．16．用一块弧长16πcm的扇形铁片，做一个高为6cm的圆锥形工件侧面（接缝忽略不计），那么这个扇形铁片的面积为cm2．17．如图，一把遮阳伞撑开时母线的长是3m，底面半径为2m，则做这把遮阳伞需用布料的面积是m2．18．圆锥形的烟囱冒的底面直径是80cm，母线长是50cm，制作100个这样的烟囱冒至少需要cm2的铁皮（结果保留π）．19．如图，在等腰△ABC中，∠BAC＝120°，AD是∠BAC的角平分线，且AD＝6，以点A为圆心，AD长为半径画弧EF，交AB于点E，交AC于点F．（1）求由弧EF及线段FC、CB、BE围成图形（图中阴影部分）的面积；（2）将阴影部分剪掉，余下扇形AEF，将扇形AEF围成一个圆锥的侧面，AE与AF正好重合，圆锥侧面无重叠，求这个圆锥的高h．20．如图，在梯形ABCD中，AD∥BC，∠C＝90°，∠BAD＝120°，AB＝AD＝4，BC＝6，以点A为圆心在这个梯形内画出一个最大的扇形（图中阴影部分）．（1）求这个扇形的面积；（2）若将这个扇形围成圆锥，求这个圆锥的底面积．21．如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连接EO、FO，若DE＝4，∠DP A＝45°（1）求⊙O的半径．（2）若图中扇形OEF围成一个圆锥侧面，试求这个圆锥的底面圆的半径．22．如图，一个圆锥形工艺品，它的高为3cm，侧面展开图是半圆．求：（1）圆锥的母线长与底面半径之比；（2）圆锥的侧面积．参考答案1．B．2．A．3．C．4．D．5．D．6．A．7．A．8．D．9．B．10．B．11．A．12．A．13．．14．4．15．6π．16．80π．17．6π．18．200000π．19．解：∵在等腰△ABC中，∠BAC＝120°，∴∠B＝30°，∵AD是∠BAC的角平分线，∴AD⊥BC，BD＝CD，∴BD＝AD＝6，∴BC＝2BD＝12，﹣S扇形EAF＝∴由弧EF及线段FC、CB、BE围成图形（图中阴影部分）的面积＝S△ABC ×6×12﹣＝36﹣12π；（2）设圆锥的底面圆的半径为r，根据题意得2πr＝，解得r＝2，这个圆锥的高h＝＝4．20．解：（1）过点A作AE⊥BC于E，则AE＝2，∵AD∥BC，∠BAD＝120°，∴扇形的面积为＝4π，（2）设圆锥的底面半径为r，则2πr＝，解得：r＝若将这个扇形围成圆锥，这个圆锥的底面积π．21．解：（1）∵弦DE垂直平分半径OA，∴CE＝DC＝DE＝2，OC＝OE，∴∠OEC＝30°，∴OC＝＝2，∴OE＝2OC＝4，即⊙O的半径为4；（2）∵∠DP A＝45°，∴∠D＝45°，∴∠EOF＝2∠D＝90°，设这个圆锥的底面圆的半径为r，∴2πr＝，解得r＝1，即这个圆锥的底面圆的半径为1．22．解：（1）设圆锥底面半径为rcm，母线为ℓcm，由题知2πr＝πℓ解得ℓ：r＝2：1答：圆锥母线与底面半径之比为2：1．（2）由题知把ℓ＝2r代入，解得r1＝﹣3（舍去），r2＝3∴ℓ＝6∴圆锥的侧面积＝πrℓ＝18π（cm2）。

中考数学《圆锥的侧面积》专题练习（附带答案）一．选择题1．用半径为6的半圆围成一个圆锥的侧面，则圆锥的底面半径等于（）A．3B．2.5C．2D．1.52．已知圆锥的底面半径为2cm，母线长为4cm，则圆锥的侧面积是（）A．8cm2B．16cm2C．16πcm2D．8πcm23．已知一圆锥母线长为8cm，其侧面展开图扇形的圆心角为90°，则圆锥底面圆的半径为（）A．1cm B．2cm C．3cm D．4cm4．如图，从一块直径为24cm的圆形纸片上，剪出一个圆心角为90°的扇形ABC，使点A，B，C都在圆周上，将剪下的扇形围成一个圆锥的侧面，则这个圆锥的底面圆的半径是（）A．3cm B．2cm C．6cm D．12cm5．如图，沿一条母线将圆锥侧面剪开并展开，得到一个扇形，若圆锥的底面圆的半径r＝2cm，扇形的圆心角θ＝120°，则该圆锥的母线长为（）A．6cm B．7cm C．8cm D．9cm6．如图，圆锥的轴截面是一个斜边为1的等腰直角三角形，则这个圆锥的侧面积是（）A．B．C．πD．π7．如图，在Rt△ABC中，∠B＝90°，AC＝5，BC＝4，以AC所在的直线为轴旋转一周所成几何体的表面积为（）A．B．C．D．12π8．一把大遮阳伞，伞面撑开时可近似地看成是圆锥形，如图，它的母线长是2.5米，底面半径为2米，则做成这把遮阳伞需要布料的面积是（）平方米（接缝不计）．A．πB．5πC．4πD．3π二．填空题9．如果把一个圆柱体橡皮泥的一半捏成与圆柱底面积相等的圆锥，则这个圆锥的高与圆柱的高的比为．10．电焊工用一个圆心角为150°，半径为24cm的扇形白铁片制作一个圆锥的侧面（假设焊接时缝隙宽度忽略不计），那么这个圆锥的底面半径为cm．11．如图，圆锥底面圆心为O，半径OA＝1，顶点为P，将圆锥置于平面上，若保持顶点P位置不变，将圆锥顺时针滚动三周后点A恰好回到原处，则圆锥的高OP＝．12．已知圆锥的底面半径为2cm，侧面积为10πcm2，则该圆锥的母线长为cm．13．用半径为30的一个扇形纸片围成一个底面半径为10的圆锥的侧面，则这个圆锥的侧面积为．14．扇形的半径为8cm，圆心角为120°，用该扇形围成一个圆锥的侧面，则这个圆锥底面圆的直径是cm．三．解答题15．如图，在梯形ABCD中，AD∥BC，∠C＝90°，∠BAD＝120°，AB＝AD＝4，BC＝6，以点A为圆心在这个梯形内画出一个最大的扇形（图中阴影部分）．（1）求这个扇形的面积；（2）若将这个扇形围成圆锥，求这个圆锥的底面积．16．有一个直径为1m的圆形铁皮，要从中剪出一个最大的圆心角为90°的扇形ABC，如图所示．（1）求被剪掉阴影部分的面积：（2）用所留的扇形铁皮围成一个圆锥，该圆锥的底面圆的半径是多少？17．如图，已知扇形AOB的圆心角为90°，面积为16π．（1）求扇形的弧长；（2）若将此扇形卷成一个无底圆锥形筒，试求这个圆锥形筒的高OH．（注：结果保留根号或π．）18．【问题】如图1、2是底面半径为1cm，母线长为2cm的圆柱体和圆锥体模型．现要用长为2πcm，宽为4cm的长方形彩纸（如图3）装饰圆柱、圆锥模型表面．已知一个圆柱和一个圆锥模型为一套，长方形彩纸共有122张，用这些纸最多能装饰多少套模型呢？【对话】老师：“长方形纸可以怎么裁剪呢？”学生甲：“可按图4方式裁剪出2张长方形．”学生乙：“可按图5方式裁剪出6个小圆．”学生丙：“可按图6方式裁剪出1个大圆和2个小圆．”老师：尽管还有其他裁剪方法，但为裁剪方便，我们就仅用这三位同学的裁剪方法！【解决】（1）计算：圆柱的侧面积是cm2，圆锥的侧面积是cm2．（2）1张长方形彩纸剪拼后最多能装饰个圆锥模型；5张长方形彩纸剪拼后最多能装饰个圆柱体模型．（3）求用122张彩纸对多能装饰的圆锥、圆柱模型套数．19．课堂上，师生一起探究知，可以用已知半径的球去测量圆柱形管子的内径．小明回家后把半径为5cm 的小皮球置于保温杯口上，经过思考找到了测量方法，并画出了草图（如图）．请你根据图中的数据，帮助小明计算出保温杯的内径．20．一个圆锥形工件的轴截面是一个等腰直角三角形，这个直角三角形的斜边长为10cm，现为这个工件刷油漆，每平方厘米要2.5g油漆，至少要多少油漆？（结果保留根号）参考答案一．选择题1．解：半圆的周长＝×2π×6＝6π∴圆锥的底面周长＝6π∴圆锥的底面半径＝＝3故选：A．2．解：底面圆的半径为2，则底面周长＝4π，侧面面积＝×4π×4＝8πcm2．故选：D．3．解：设圆锥底面半径为rcm那么圆锥底面圆周长为2πrcm所以侧面展开图的弧长为＝4πcm则2πr＝4π解得：r＝2故选：B．4．解：AB＝＝＝12cm∴＝＝6π∴圆锥的底面圆的半径＝6π÷（2π）＝3cm．故选：A．5．解：圆锥的底面周长＝2π×2＝4πcm设圆锥的母线长为R，则：＝4π解得R＝6．故选：A．6．解：∵圆锥的轴截面是一个斜边为1的等腰直角三角形∴底面半径＝0.5，母线长为，底面周长＝π∴圆锥的侧面积＝×π×＝．故选：A．7．解：作BH⊥AC于H，如图AB＝＝3∵BH•AC＝AB•BC∴BH＝＝∴以AC所在的直线为轴旋转一周所成几何体的表面积＝•2π••4+•2π••3＝π．故选：A．8．解：圆锥的底面周长＝2πr＝2π×2＝4π∵圆锥的底面周长等于圆锥的侧面展开扇形的弧长∴圆锥的侧面积＝lr＝×4π×2.5＝5π故选：B．二．填空题9．解：设圆柱的高为a，圆锥的高为b，圆柱底面积为S根据题意得S•a＝•S•b所以b：a＝3：2．故答案为：3：2．10．解：设这个圆锥的底面半径为r根据题意得2πr＝解得r＝10．答：这个圆锥的底面半径为10cm．故答案为10．11．解：当圆锥顺时针滚动三周后点A恰好第一次回到原处，根据题意3π•1＝π•P A∴P A＝3∴OP＝＝2当圆锥顺时针滚动三周后点A恰好第二次回到原处，根据题意π•1＝π•P A∴P A＝∴OP＝＝＝综上所述，OP的长为2或．故答案为2或．12．解：设圆锥的母线长为Rcm圆锥的底面周长＝2π×2＝4π（cm）则×4π×R＝10π解得，R＝5故答案为：5．13．解：这个圆锥的侧面积为S侧＝•2πr•l＝πrl＝π×10×30＝300π故答案为：300π．14．解：设此圆锥的底面半径为r，由题意，得2πr＝解得r＝cm．所以直径为cm故答案为：．三．解答题15．解：（1）过点A作AE⊥BC于E则AE＝AB sin B＝4×＝2∵AD∥BC，∠BAD＝120°∴扇形的面积为＝4π（2）设圆锥的底面半径为r，则2πr＝解得：r＝若将这个扇形围成圆锥，这个圆锥的底面积π．16．解：（1）如图，连接BC∵∠BAC＝90°∴BC为⊙O的直径，即BC＝1m又∵AB＝AC∴．∴（平方米）（2）设底面圆的半径为r，则∴．圆锥的底面圆的半径长为米．17．解：（1）设扇形的半径是R，则＝16π解得：R＝8设扇形的弧长是l，则lR＝16π，即4l＝16π解得：l＝4π．（2）圆锥的底面圆的半径为r根据题意得2πr＝，解得r＝2所以个圆锥形桶的高＝＝2．18．解：（1）圆柱的地面底面周长是2π，则圆柱的侧面积是2π×2＝4πcm2，圆锥的侧面积是×2π×2＝2πcm2；（2）圆柱的底面积是：πcm2，则圆柱的表面积是：6πcm2，圆锥的表面积是：3πcm2．一张纸的面积是：4×2π＝8π则1张长方形彩纸剪拼后最多能装饰2个圆锥模型；5张长方形彩纸剪拼后最多能装饰6个圆柱体模型（3）设做x套模型，则每套模型中做圆锥的需要张纸，作圆柱需要张纸∴+≤122解得：x≤∵x是6的倍数，取x＝90，做90套模型后剩余长方形纸片的张数是122﹣（45+75）＝2张2张纸够用这三位同学的裁剪方法能做一套模型．∴最多能做91套模型．故答案是：4π，2π；2，6．19．解：连OD．∵EG＝20﹣12＝8∴OG＝8﹣5＝3∴GD＝4∴AD＝2GD＝8cm．答：保温杯的内径为8cm．20．解：∵△ABC为等腰直角三角形，BC＝10∴AC＝BC＝5∴圆锥的表面积＝π•（）2+π•5•5＝（25π+25π）cm2∵每平方厘米要2.5g油漆∴所需油漆的量＝（25π+25π）×2.5＝（+1）π（g）．。

苏教版数学九年级上册说课稿《2-8圆锥的侧面积》一. 教材分析《圆锥的侧面积》是苏教版数学九年级上册第五章“圆锥”的一部分。

这部分内容是在学生已经掌握了圆锥的基本概念、性质和圆锥的体积计算的基础上进行教学的。

本节课的主要内容是引导学生通过观察、思考、探究、交流等方式，理解和掌握圆锥的侧面积的计算方法和应用。

教材中通过生活中的实例引入圆锥的侧面积的概念，接着引导学生通过展开圆锥的侧面，推导出圆锥的侧面积的计算公式，最后通过练习，巩固学生对圆锥侧面积的理解和应用。

二. 学情分析九年级的学生已经具备了一定的空间想象能力和逻辑思维能力，对圆锥的基本概念和性质有一定的了解。

但是，由于圆锥的侧面积比较抽象，学生理解和掌握起来可能会有一定的困难。

因此，在教学过程中，我将会注重引导学生通过观察、操作、思考、交流等方式，自主探究圆锥侧面积的计算方法和应用，帮助学生克服困难，提高学生对圆锥侧面积的理解和应用能力。

三. 说教学目标1.知识与技能目标：让学生理解和掌握圆锥的侧面积的计算方法和应用。

2.过程与方法目标：培养学生通过观察、操作、思考、交流等方式自主探究问题的能力。

3.情感态度与价值观目标：激发学生学习数学的兴趣，培养学生的团队合作意识和克服困难的精神。

四. 说教学重难点1.教学重点：圆锥的侧面积的计算方法和应用。

2.教学难点：圆锥的侧面积的推导过程和理解。

五. 说教学方法与手段在教学过程中，我将采用引导探究法、合作交流法、直观演示法等教学方法，利用多媒体课件、圆锥模型等教学手段，帮助学生理解和掌握圆锥的侧面积。

六. 说教学过程1.导入：通过生活中的实例，引导学生思考圆锥的侧面积的概念。

2.探究：引导学生通过展开圆锥的侧面，观察和思考圆锥侧面积的计算方法。

3.讲解：讲解圆锥侧面积的计算公式，并引导学生通过练习，巩固对圆锥侧面积的理解。

4.应用：通过实际问题，引导学生运用圆锥侧面积的知识解决问题。

5.小结：对本节课的内容进行总结，强调圆锥侧面积的计算方法和应用。

5.10圆锥的侧面积测试题一．选择题（共8小题）1．（2015•宁波）如图，用一个半径为30cm，面积为300πcm2的扇形铁皮，制作一个无底的圆锥（不计损耗），则圆锥的底面半径r为（）A．5cm B． 10cm C． 20cm D．5πcm（1题图）（4题图）（6题图）2．（2015•凉山州）将圆心角为90°，面积为4πcm2的扇形围成一个圆锥的侧面，则所围成的圆锥的底面半径为（）A．1cm B． 2cm C． 3cm D．4cm 3．（2015•湖州）若一个圆锥的侧面展开图是半径为18cm，圆心角为240°的扇形，则这个圆锥的底面半径长是（）A．6cm B． 9cm C． 12cm D．18cm 4．（2015•河池）如图，用一张半径为24cm的扇形纸板制作一顶圆锥形帽子（接缝忽略不计），如果圆锥形帽子的底面半径为10cm，那么这张扇形纸板的面积是（）A．240πcm2B．480πcm2C．1200πcm2D．2400πcm2 5．（2015•乌鲁木齐）圆锥的侧面展开图是一个弧长为12π的扇形，则这个圆锥底面积的半径是（）A．24 B． 12 C． 6 D．3 6．（2015•德州）如图，要制作一个圆锥形的烟囱帽，使底面圆的半径与母线长的比是4：5，那么所需扇形铁皮的圆心角应为（）A．288°B．144°C．216°D．120°7．（2015•恩施州模拟）如图，扇形OAB是圆锥的侧面展开图，若小正方形方格的边长均为1厘米，则这个圆锥的底面半径为（）厘米．A．B．C．D．（7题图）（8题图）8．（2015•泰安模拟）如图，是一个工件的三视图，则此工件的全面积是（）A．60πcm2B．90πcm2C．96πcm2D．120πcm2二．填空题（共8小题）9．（2015•黔西南州）已知圆锥的底面圆半径为3，母线长为5，则圆锥的全面积是．10．（2015•北海）用一个圆心角为120°，半径为6的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径是．11．（2015•孝感）已知圆锥的侧面积等于60πcm2，母线长10cm，则圆锥的高是cm．12．（2015•徐州）用一个圆心角为90°，半径为4的扇形围成一个圆锥的侧面，该圆锥底面圆的半径．13．（2015•黑龙江）如图，从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC（A、B、C三点在⊙O上），将剪下来的扇形围成一个圆锥的侧面，则该圆锥的底面圆的半径是米．13题图（15题图）（16题图）14．（2015•呼和浩特）一个圆锥的侧面积为8π，母线长为4，则这个圆锥的全面积为．15．（2015•庆阳）如图，Rt△ABC中，∠ACB=90°，AC=BC=2，若把Rt△ABC 绕边AB所在直线旋转一周，则所得几何体的表面积为（结果保留π）．16．（2015•烟台）如图，将弧长为6π，圆心角为120°的圆形纸片AOB围成圆锥形纸帽，使扇形的两条半径OA与OB重合（粘连部分忽略不计）则圆锥形纸帽的高是．三．解答题（共4小题）17．（2015•淮北模拟）一个几何体的三视图如图所示，根据图示的数据计算出该几何体的表面积．18．（2015•珠海校级一模）如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径r=2cm，扇形的圆心角θ=120°，求该圆锥的高h 的长．19．（2015春•萧山区校级月考）已知一个几何体的三视图如图，根据图示的数据计算该几何体的全面积及侧面展开图的圆心角（结果保留π）．20．（2015•大庆模拟）如图所示的粮仓可以看成圆柱体与圆锥体的组合体，已知其底面半径为6米，高为4米，下方圆柱高为3米．（1）求该粮仓的容积；（2）求上方圆锥的侧面积．（计算结果保留根号）参考答案一．选择题（共8小题）1．B．2．A．3．C．4．5．C．6．A．7．B．8．C．二．填空题（共8小题）9．24π．10． 2 ．11．8 12． 1 ．13．14．12π．15．8π16．6三．解答题（共4小题）17．解：由三视图可知该几何体是圆锥，圆锥的高为12，圆锥的底面圆的半径为5，所以圆锥的母线长==13，所以圆锥的表面积=π•52+•2π•5•13=90π．18．解：如图，由题意得：，而r=2，∴AB=12，∴由勾股定理得：AO2=AB2﹣OB2，而AB=12，OB=2，∴AO=．即该圆锥的高为2．19．解：∵如图所示可知，圆锥的高为4，底面圆的直径为6，∴圆锥的母线为：5，∴根据圆锥的侧面积公式：πrl=π×3×5=15π，底面圆的面积为：πr2=9π，∴该几何体的表面积为24π．20．解：（1）体积V=π×62×3+×π×62×（4﹣3）=108π+12π=120π；（2）圆锥的母线长为l==，所以圆锥的侧面积为s=π×6×=6π．。

2.8圆锥的侧面积一、基础训练1． 若圆锥的底面圆半径为r ，母线长为l ，则圆锥的侧面积S 圆锥侧＝ ，2． 若圆锥的底面圆半径为3，母线长为5，则圆锥的侧面积为3． 若圆锥的底面圆半径为5，侧面积为60π，则母线长为，侧面展开扇形的圆心角为°．4． 若用半径为9，圆心角为120°的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的底面半径是 ． 二、典型例题例1：如图，一个圆锥的高为，侧面展开图是半圆．求：（1）圆锥的母线长与底面半径之比；（2）求BAC ∠的度数；（3）圆锥的侧面积（结果保留π）．分析：圆锥的底面周长是圆锥侧面展开图的弧长，由此可以得到母线长和底面半径的关系，再根据直角三角形的性质，如果直角边是斜边的一半，那么这条直角边所对的角是30°，求出BAC ∠的度数；再由勾股定理列方程求出底面半径，进而求出扇形侧面积． 例2：若一个圆锥的底面积是侧面积的13，则该圆锥侧面展开图的圆心角度数是多少度． 分析：题目中没有具体数字，要求侧面展开图圆心角的度数需要找出底面半径和母线长的关系． 三、拓展提升：如图，在△ABC 中，∠C ＝90°，AC ＝8，BC ＝6，以这个三角形的一边所在的直线为轴旋转一周，求所得几何体的全面积．分析 本题有三种情形：分别如图（1）、（2）、（3）所示．四、课后作业1．圆锥的底面半径为8，母线长为9，则该圆锥的侧面积为 ． 2．已知圆锥的底面半径为10，侧面积是300π，则这个圆锥的母线长为 ．ABCAB CABC（1）（2）（3）3． 圆锥的底面直径是8，母线长是12，则这个圆锥侧面展开图的扇形圆心角是 °． 4． 如图已知扇形AOB 的半径为6cm ，圆心角的度数为120°，若将此扇形围成一个圆锥，则围成的圆锥的侧面积为 ．5如图，有一圆锥形粮堆，其主视图是边长为6m 的正三角形ABC ，母线AC 的中点P 处有一老鼠正在偷吃粮食．小猫从B 处沿圆锥表面去偷袭老鼠，求小猫所经过的最短路程（结果保留π）6． 如图，已知△ABC 中，∠ABC ＝90°，∠C ＝60°，边AB ＝6cm ． （1）求边AC 和BC 的长；（2）求以直角边AB 所在直线l 为轴旋转一周所得几何体的侧面积．（结果保留π）7． 下图是一纸杯，它的母线AC 和EF 延长后形成的立体图形是圆锥．该圆锥的侧面展开图形是扇形OAB ．经测量，纸杯上开口圆的直径为6cm ，下底面直径为4cm ，母线长EF ＝8cm ．求扇形OAB 的圆心角及这个纸杯的表面积．（结果保留π）一、基础训练 1. πrl ，πrl ＋πr 2．C 第4题120BO A 6cmＯ 第5题2.15π，24π．3.12，150°．4. 3二、典型例题例1. （1）设此圆锥的高为h ，底面半径为r ，母线长AC l =． ∵2ππr l =，∴2lr=． （2）∵2lr=，∴圆锥高与母线的夹角为30°，则60BAC ∠=°（3）由图可知222l h r h =+=，，∴222(2)r r =+，即22427r r =+．解得 3cm r =．∴26cm l r ==．∴圆锥的侧面积为22π18π(cm )2l =． 例2. 设底面半径为r ，母线长为R,则底面积为2r π，侧面积为：122r R π⨯g ,因为他们的比值为13，所以R=3r ，再由弧长公式得方程：32180180n R n rr πππ==g ，解得：n =120.三、拓展提升如图（1），当以AC 所在直线为轴旋转一周时，全面积为96π；如图（2），当以BC 所在直线为轴旋转一周时，全面积为144π；如图（3），当以AB 所在直线为轴旋转一周时，全面积为3365 π．四．课后作业 1．72π 2．30． 3. 120 4. 212πcm 5. 3 5 ．6. （1）在Rt △ABC 中，60C ∠=o， 30BAC ∠=o∴，2AC BC =∴．设BC x =，则2AC x =．根据勾股定理有：222AC AB BC =+．即：222(2)6x x =+，x =∴ BC =∴，AC =（2）22l r BC ===g ∵ππ，∴R AC ==∴12S lR =侧1242=⨯⨯=π（cm 2）． 答：旋转后所得几何体的侧面积为24π cm 27. 由题意可知：»6AB =π，»4CD =π．设AOB n ∠=o ，AO R =，则8CO R =-． 由弧长公式得：6180n R =ππ，(8)4180n R -=ππ．解方程组6180,41808.nR nR n ⨯=⎧⎨⨯=-⎩得45,24.n R =⎧⎨=⎩∴扇形OAB 的圆心角是45o ．∵24R =，816R -=，1416322OCD S =⨯⨯=扇形∴ππ 1624722OAB S =⨯⨯=扇形ππ，∴7232OAB OCD S S S =-=-纸杯侧面积扇形扇形ππ40=π．∵224S ==g 纸杯底面积ππ．∴40444S =+=纸杯表面积πππ．。

圆锥的侧面积和全面积习题精选一、选择题1．一个扇形的半径为300厘米，圆心角为120°．用它做成一个圆锥的侧面，则圆锥的高等于（）．A．20π厘米B．10π厘米C．20厘米D．2．下列图形沿着某一直线旋转180°后，一定能形成圆锥的是（）．A．直角三角形B．等腰三角形C．矩形D．扇形3．将图（1）中的三角形绕直线l旋转一周，可以得到如图（2）所示的立体图形的是（）．4．圆锥的锥角为90°，则圆锥的侧面展开图中扇形的圆心角的度数为（）．A．90°︒B．C．180°︒D．51，则圆锥侧面展开图的面积为（）．A．2πB．πC．D6．若圆锥的高与底面圆的直径相等，则底面积与侧面积之比为（）．A．1B．1：2C．1D．1；1.57．用半径l0厘米、圆心角215°的扇形做成一个圆锥的侧面，则这个圆锥的高为（）厘米．A．4B．8C．6D8．圆锥的侧面积为8π平方厘米，其轴截面为一等边三角形，则该轴截面的面积为（）．A．B．C．平方厘米D．平方厘米二、填空题1．一个圆锥的高为l0厘米，侧面展开图是一个半圆，则此圆锥的侧面积为______平方厘米．2．圆锥的轴截面为等边三角形，且母线长为5厘米，则其锥角为_______，轴截面面积为________，圆锥侧面积为___________。

3．圆锥底面半径为1厘米，侧面展开图面积为2π平方厘米，则侧面展开图的圆心角为________。

4．如图，圆锥形的烟囱帽的底面直径是80厘米，母线长为50厘米，则这个烟囱帽的展开图的面积是_______平方厘米（结果保留π）．三、解答题1．已知扇形的圆心角为120°，面积为300 平方厘米．（1）求扇形的弧长；（2）若把此扇形卷成一个圆锥，那么这个圆锥的轴截面面积是多少?2．如图，矩形ABCD中，AB=1，若直角三角形ABC绕AB旋转所得的圆锥侧面积和矩形ABCD绕AB旋转所得圆柱的侧面积相等，求BC的长．3．如图2，粮仓的顶部是圆锥形，这个圆锥形的底面周长为36米，母线长为8米．为防雨需在粮仓顶部铺上油毡，如果按用料的10％计接头重合部分，那么这座粮仓的实际须用油毡面积是多少?4．如图，有一个直径为1米的圆形铁皮，要从中剪出一个最大的圆心角为90°的扇形ABC．（1）求剩下的阴影部分面积；（2）用所留的扇形铁皮围成一个圆锥，该圆锥底面圆的半径是多少?5．如图，将钝角三角形ABC绕直线l旋转一周，那么旋转以后得到一个什么样的几何体?试求该几何体的全面积．（已知∠BCA ＝30°，∠BAD ＝45°，BC ＝10）答案：一、1．D 解析：由题意，知AO 为圆锥的高，设AO=h ，BO 为圆的半径，且BO=R ，AB 为圆锥的每线设为l 。