第二篇泊松过程

Poisson 过程的模拟和检验一、 实验目的1、理解掌握Poisson 过程的理论，了解随机过程的模拟实现技术；2、学习并掌握在实际中如何检验给定的随机过程是否为Poisson 过程。

二、 实验内容1、利用C 语言、MATLAB 等工具，结合Poisson 过程等相关结论，模拟Poisson 过程；2、查找资料、学习关于Poisson 过程假设检验的相关知识，检验上述模拟实现的到达过程是否满足Poisson 过程的定义。

三、 作业要求提交实验报告电子版，说明模拟实现的过程，检验原理、步骤等以及实现过程；提交程序源代码。

四、 实验原理1、泊松过程（1）计数过程如果用)(t X 表示[0，t ]内随机事件发生的总数，则随机过程{)(t X ，0≥t }称为一个计数过程。

且满足：1）0)(≥t X ；2）)(t X 是整数值；3）对任意两个时刻210t t <≤，有12()()X t X t ≤；4）对任意两个时刻210t t <≤。

)()(12t X t X -等于在区间],(21t t 中发生的事件的个数。

（2）泊松过程设随机过程{()N t ，0≥t }是一个计数过程，满足1）(0)0N =；2）()N t 是独立增量过程；3）对任一长度为t 的区间中事件的个数，服从均值为t λ（0>λ）的泊松分布，即对一切0,≥t s ，有(){()()},0,1,2,!kt t P N t s N s k e k k λλ-+-===则称()N t 为具有参数λ的Poisson(泊松)过程。

（3）到达时间间隔n T 的分布设{()X t ，0≥t }为泊松过程，()X t 表示到时刻t 为止已发生的事件的总数；,(1,2,3,)n W n =表示第n 次事件发生的时刻；,(1,2,3,)n T n = 表示第n 次与第n-1次事件发生的时间间隔。

显然，121nn n i i W T T T T ==+++=∑定理3.2 设{()X t ，0≥t }是参数为λ（0>λ）的泊松过程，则到达时间间隔序列12T T ，，是相互独立的随机变量序列，且都有相同的均值为λ/1的指数分布。

泊松定理公式推导过程
泊松定理公式推导过程：假设时间T是一个线,事件a发生在线T上的某一个点上,不妨先把点看成是一跟无限短的线。

将T进行n 等分均分,并保证每等分的情况E{发生一次,没有发生}。

就可以得出一个公式。

n就是区间的个数,但是由于题目讨论的是线上的点,所以以可以让n趋向于无穷大,那区间足够小就可以视作一个点。

p就是a 发生在区间上的概率。

接着继续分析,可以得到两个公式。

点的概率公式:即事件发生的数学期望。

limn→8n时间段T内发生k次事件的概率:P(x=k)=Скрk(1=р)n-k。

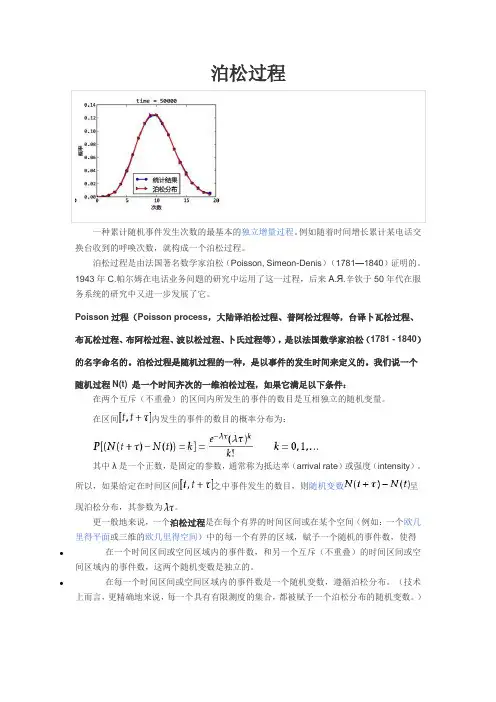
泊松过程一种累计随机事件发生次数的最基本的独立增量过程。

例如随着时间增长累计某电话交换台收到的呼唤次数，就构成一个泊松过程。

泊松过程是由法国著名数学家泊松（Poisson, Simeon-Denis）（1781—1840）证明的。

1943年C.帕尔姆在电话业务问题的研究中运用了这一过程，后来Α.Я.辛钦于50年代在服务系统的研究中又进一步发展了它。

Poisson过程（Poisson process，大陆译泊松过程、普阿松过程等，台译卜瓦松过程、布瓦松过程、布阿松过程、波以松过程、卜氏过程等），是以法国数学家泊松（1781 - 1840）的名字命名的。

泊松过程是随机过程的一种，是以事件的发生时间来定义的。

我们说一个随机过程N(t) 是一个时间齐次的一维泊松过程，如果它满足以下条件：在两个互斥（不重叠）的区间内所发生的事件的数目是互相独立的随机变量。

在区间内发生的事件的数目的概率分布为：其中λ是一个正数，是固定的参数，通常称为抵达率（arrival rate）或强度（intensity）。

所以，如果给定在时间区间之中事件发生的数目，则随机变数呈现泊松分布，其参数为。

更一般地来说，一个泊松过程是在每个有界的时间区间或在某个空间（例如：一个欧几里得平面或三维的欧几里得空间）中的每一个有界的区域，赋予一个随机的事件数，使得•在一个时间区间或空间区域内的事件数，和另一个互斥（不重叠）的时间区间或空间区域内的事件数，这两个随机变数是独立的。

•在每一个时间区间或空间区域内的事件数是一个随机变数，遵循泊松分布。

（技术上而言，更精确地来说，每一个具有有限测度的集合，都被赋予一个泊松分布的随机变数。

）泊松过程是莱维过程（Lévy process）中最有名的过程之一。

时间齐次的泊松过程也是时间齐次的连续时间Markov过程的例子。

一个时间齐次、一维的泊松过程是一个纯出生过程，是一个出生-死亡过程的最简单例子。

第二讲 泊松过程1．随机过程和有限维分布族现实世界中的随机过程例子：液体中，花粉的不规则运动：布朗运动；股市的股票价格； 到某个时刻的电话呼叫次数；到某个时刻服务器到达的数据流数量，等。

特征：都涉及无限多个随机变量，且依赖于时间。

定义（随机过程） 设有指标集T ，对T t ∈都有随机变量)(t X 与之对应，则称随机变量族}),({T t t X ∈为随机过程。

注 一个随机过程是就是一个二元函数E T t X →⨯Ωω:),(。

固定ω，即考虑某个事件相应的随机变量的值，得到函数R T t X →:),(ω称为样本函数或轨道或一个实现。

映射的值域空间E 称为状态空间。

例 随机游动(离散时间，离散状态)质点在直线上每隔单位时间位置就发生变化，分别以概率p 或概率p -1向正或负向移动一个单位。

如果以n S 记时刻n 质点所处的位置，那么就得到随机过程{,0}n S n ≥。

这里指标集},1,0{ =T ，状态空间},1,0,1,{ -=E 。

如果记n X 为时刻n ，质点的移动，那么{,1}n X n ≥也是随机过程。

两个过程的区别：{}n S 不独立；{}n X 独立； 两个过程的关系：01nn kk S S X==+∑习题 计算n ES 和n DS （设00S =）。

提示 利用∑==nk kn XS 1，其中k X 是时刻k 的移动方式。

习题 设从原点出发，则()/2()/2()/2,2()0,21n k n k n k n n C q p n k iP S k n k i +-+⎧+===⎨+=-⎩。

例 服务器到达的数据流(连续时间，离散状态)在],0[t 内，到达服务器的数据包个数记为)(t N ，那么}0),({≥t t N 也是个随机过程，其指标集}{+∈=R t T ，状态空间},1,0{ =E 。

例 布朗运动（连续时间，连续状态）直线上质点的位移是连续的。

在时刻t 的位置为t X 。

泊松过程参数估计全文共四篇示例，供读者参考第一篇示例：泊松过程是一种常见的随机过程，其在很多领域都有着广泛的应用，比如通信网络、金融市场、医学统计学等。

泊松过程最基本的特点就是事件在时间上是随机地不断发生的，且事件之间是相互独立的。

泊松过程的一个关键参数就是事件的发生率，即单位时间内事件发生的次数，通常用λ来表示。

在实际应用中，我们常常需要对泊松过程的参数进行估计，以便更好地理解、分析和预测事件的发生情况。

参数估计的目的就是通过已有的样本数据，来估计未知的参数值。

泊松过程的参数估计方法有很多种，比如极大似然估计、贝叶斯估计等，下面我们就来详细介绍一下这些方法。

首先我们来介绍一下极大似然估计（Maximum Likelihood Estimation，简称MLE）。

极大似然估计是一种常用的参数估计方法，其目标是选择最能够使观测到的数据出现的概率最大的参数值。

对于泊松过程来说，假设我们有一组事件的发生时间数据，我们可以通过计算这些事件的时间间隔来得到事件发生的频率，然后通过极大似然估计的方法来估计λ的值。

具体来说，设有n个事件发生，分别在时间t1,t2,...,tn发生，时间间隔分别为Δt1=t1，Δt2=t2-t1,...,Δtn=tn-tn-1。

假设事件发生率为λ，那么事件发生时的概率密度函数为P(Δt)=λe^(-λΔt)，当所有事件都发生时的联合概率密度函数为L(λ)=∏(i=1,n)λe^(-λΔti)。

然后通过最大化L(λ)来得到λ的估计值。

除了极大似然估计外，贝叶斯估计也是一种常见的参数估计方法。

贝叶斯估计是一种基于贝叶斯定理的方法，其核心思想是先验概率和后验概率的更新。

对于泊松过程来说，我们可以引入一个先验分布作为事件发生率λ的先验信息，然后通过贝叶斯定理来更新这个先验分布，得到后验分布，从而估计λ的值。

我们可以假设λ服从一个指数分布，即先验分布为P(λ)=exp(-λ)，那么在得到观测数据后，我们可以根据贝叶斯定理得到后验分布为P(λ|data)∝L(λ)×P(λ)，然后通过后验分布来估计λ的值。