随机过程 第二章 泊松过程
- 格式:ppt
- 大小:481.00 KB
- 文档页数:25



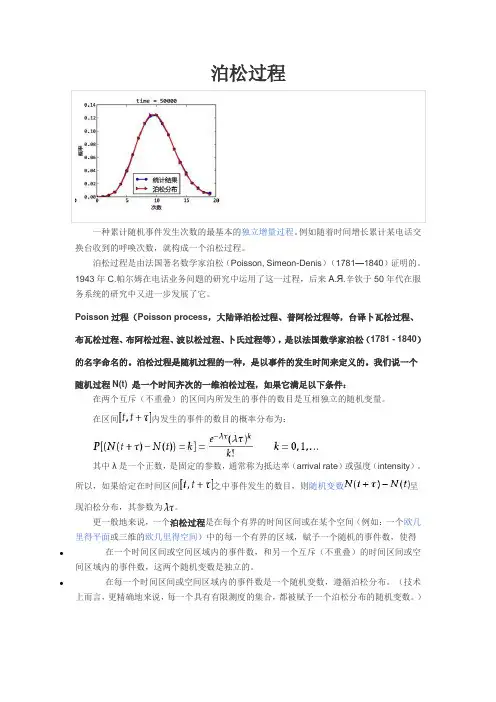
泊松过程一种累计随机事件发生次数的最基本的独立增量过程。
例如随着时间增长累计某电话交换台收到的呼唤次数,就构成一个泊松过程。
泊松过程是由法国著名数学家泊松(Poisson, Simeon-Denis)(1781—1840)证明的。
1943年C.帕尔姆在电话业务问题的研究中运用了这一过程,后来Α.Я.辛钦于50年代在服务系统的研究中又进一步发展了它。
Poisson过程(Poisson process,大陆译泊松过程、普阿松过程等,台译卜瓦松过程、布瓦松过程、布阿松过程、波以松过程、卜氏过程等),是以法国数学家泊松(1781 - 1840)的名字命名的。
泊松过程是随机过程的一种,是以事件的发生时间来定义的。
我们说一个随机过程N(t) 是一个时间齐次的一维泊松过程,如果它满足以下条件:在两个互斥(不重叠)的区间内所发生的事件的数目是互相独立的随机变量。
在区间内发生的事件的数目的概率分布为:其中λ是一个正数,是固定的参数,通常称为抵达率(arrival rate)或强度(intensity)。
所以,如果给定在时间区间之中事件发生的数目,则随机变数呈现泊松分布,其参数为。
更一般地来说,一个泊松过程是在每个有界的时间区间或在某个空间(例如:一个欧几里得平面或三维的欧几里得空间)中的每一个有界的区域,赋予一个随机的事件数,使得•在一个时间区间或空间区域内的事件数,和另一个互斥(不重叠)的时间区间或空间区域内的事件数,这两个随机变数是独立的。
•在每一个时间区间或空间区域内的事件数是一个随机变数,遵循泊松分布。
(技术上而言,更精确地来说,每一个具有有限测度的集合,都被赋予一个泊松分布的随机变数。
)泊松过程是莱维过程(Lévy process)中最有名的过程之一。
时间齐次的泊松过程也是时间齐次的连续时间Markov过程的例子。
一个时间齐次、一维的泊松过程是一个纯出生过程,是一个出生-死亡过程的最简单例子。


第二讲 泊松过程1.随机过程和有限维分布族现实世界中的随机过程例子:液体中,花粉的不规则运动:布朗运动;股市的股票价格; 到某个时刻的电话呼叫次数;到某个时刻服务器到达的数据流数量,等。
特征:都涉及无限多个随机变量,且依赖于时间。
定义(随机过程) 设有指标集T ,对T t ∈都有随机变量)(t X 与之对应,则称随机变量族}),({T t t X ∈为随机过程。
注 一个随机过程是就是一个二元函数E T t X →⨯Ωω:),(。
固定ω,即考虑某个事件相应的随机变量的值,得到函数R T t X →:),(ω称为样本函数或轨道或一个实现。
映射的值域空间E 称为状态空间。
例 随机游动(离散时间,离散状态)质点在直线上每隔单位时间位置就发生变化,分别以概率p 或概率p -1向正或负向移动一个单位。
如果以n S 记时刻n 质点所处的位置,那么就得到随机过程{,0}n S n ≥。
这里指标集},1,0{ =T ,状态空间},1,0,1,{ -=E 。
如果记n X 为时刻n ,质点的移动,那么{,1}n X n ≥也是随机过程。
两个过程的区别:{}n S 不独立;{}n X 独立; 两个过程的关系:01nn kk S S X==+∑习题 计算n ES 和n DS (设00S =)。
提示 利用∑==nk kn XS 1,其中k X 是时刻k 的移动方式。
习题 设从原点出发,则()/2()/2()/2,2()0,21n k n k n k n n C q p n k iP S k n k i +-+⎧+===⎨+=-⎩。
例 服务器到达的数据流(连续时间,离散状态)在],0[t 内,到达服务器的数据包个数记为)(t N ,那么}0),({≥t t N 也是个随机过程,其指标集}{+∈=R t T ,状态空间},1,0{ =E 。
例 布朗运动(连续时间,连续状态)直线上质点的位移是连续的。
在时刻t 的位置为t X 。




随机过程的分支过程和泊松过程随机过程,指的是随时间而变化的一系列随机事件的集合。
随机过程的数学模型可以用随机变量的集合来描述。
其中,分支过程(branching process)和泊松过程(Poisson process)是随机过程中比较经典并且应用广泛的两种模型。
一、分支过程分支过程最早出现在爱尔兰数学家戈尔登的研究中。
他在研究人口增长的过程中发现,如果假设每个人在他的有生之年内可以产生若干个子女,那么就可以把人口增长的过程看作是一个分支过程。
分支过程是一类离散时间的随机过程,可以描述由一个个独立的、概率相同的“父代”产生的“子代”数目的随机变化过程。
具体来说,在分支过程中,每个父代独立地产生一个随机整数,表示它将会产生的子代数目。
每个子代的产生也是独立的,并且都遵循与父代相同的分布。
这个过程一直持续下去,一直到所有的后代都无法再产生新的子代为止。
对于一个分支过程,我们可以定义一个生成函数G(x),表示从一个父代生成的所有子代的数目的概率分布。
对于一个父代可以生成k个后代的概率为pk,则G(x)可以表示为:G(x) = p0 + p1x + p2x2 + ... + pnxn其中,pn表示最后一代后代数目为n的概率。
我们可以根据这个生成函数来计算分支过程的很多性质,如在每个时刻,所有后代的数目的期望、方差和协方差等等。
二、泊松过程泊松过程是一个连续时间的随机过程,它具有无记忆性(memorylessness)和独立增量(independent increments)的性质,这使得它成为了极其重要的一种数学模型。
在泊松过程中,事件发生的时间无规律,但是平均每单位时间内事件发生的次数是固定的。
具体来说,对于一个泊松过程,我们定义一个速率参数λ,表示在单位时间内事件发生的平均次数。
我们假设事件是独立发生的,并且事件发生的时间间隔服从指数分布。
这样,我们就可以用泊松分布来描述在任意时间段内事件发生的次数。

应用随机过程实验2—泊松过程一.准备知识1.泊松过程2.非齐次泊松过程3. 复合泊松过程二.作业1. 设()1X t 和()2X t 分别是参数为1λ和2λ的相互独立的泊松过程,(1)模拟()1X t 和()2X t ,并画图;(2)生成随机过程()()()12Y t =X +X t t ,并画图;(3)计算(){}Y t ,t 0≥ 的平均到达率与+1λ2λ的相对误差。
2. 设到达某商店的顾客组成强度为λ的泊松过程,每个顾客购买商品的概率为p ,且与其他顾客是否购买商品无关,假设每位购买商品的顾客的花费i X 独立同分布,且服从正态分布2X (,)iN μσ,1,2,3,i = ,令()Y t 是t 时刻购买商品的顾客数,()Z t 是t 时刻商品的营业额,0t ≥ ,(1)试模拟随机过程(){},0Y t t ≥,并画图,计算随机过程(){},0Y t t ≥ 的均值函数与pt λ的相对误差;(2)试模拟随机过程(){},0Z t t ≥,并画图,计算随机过程(){}t ,t 0Z ≥ 的均值函数与pt λμ的相对误差。
3. 某路公共汽车从早晨5时到晚上9时有车发出,乘客流量如下:5时按平均乘客为200人/小时计算;5时至8时乘客平均到达率线性增加,8时到达率为1400人/小时;8时至18时保持平均到达率不变;18时到21时到达率线性下降,到21时为200人/小时,假定乘客数在不重叠的区间内是相互独立的,令()X t 是t 时刻到达公共汽车的总人数,(1)计算早晨5时到晚上9时的乘客到达率,并画图;(2)模拟从早晨5时到晚上9时的乘客到达过程(){}X t ,t 0≥。
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注)。
随机过程——泊松过程计数过程 在(0,t)内出现事件A的总数所组成的过程{N(t),t>0}称为计数过程。
如果⽤N(t)表⽰到时刻t为⽌已发⽣的“事件A”的总数,若N(t)满⾜下列条件:1. N(t)≥02. N(t)取正整数值3. 对任意两个时刻t1<t2,有N(t1)≤N(t2)4. 对任意两个时刻t1<t2,N(t2)-N(t1)等于在区间(t1,t2]中发⽣的“事件A”的次数 则随机过程{N(t),t≥0}称为⼀个计数过程。
注意:如果在不相交的时间区间中发⽣的事件个数是独⽴的,则称计数过程有独⽴增量。
若在任⼀时间区间中发⽣的事件个数的分布只依赖于时间区间的长度,则称计数过程有平稳增量。
独⽴增量过程 如果在不相交的时间间隔内出现事件A的次数是互相统计独⽴的则A事件的计数过程为独⽴增量过程。
平稳(齐次)增量计数过程 在时间间隔(t,t+s)内出现事件A的次数[N(t+s)-N(t)]仅与s有关⽽与t⽆关,则称N(t)为平稳增量计数过程。
泊松过程 设随机过程{X(t),t≥0}是⼀个计数过程,满⾜1. X(0)=02. X(t)是独⽴增量过程3. 对任⼀长度为t的区间中事件的个数服从参数为λt(λ>0)的泊松分布,即对⼀切s,t≥0,有P{X(t+s)-X(s)=k}=(λt)k/(k!).exp(-λt)(其中k=0,1,2,…) 则称X(t)为具有参数λ的泊松过程。
注意:从条件3可知泊松过程有平稳增量,且E[X(t)]=λt并称λ为此过程的⽣起率或强度(单位时间内发⽣事件的平均个数)。
说明: 要确定计数过程是泊松过程,必须证明它满⾜三个条件:条件1只是说明事件的计数是从时刻t=0开始条件2通常可从对过程的了解的情况去直接验证然⽽全然不清楚如何去确定条件3是否满⾜ 为此给出⼀个与泊松过程等价的定义定义 设随机过程{X(t),t≥0}是⼀个计数过程,参数为λ(λ>0),满⾜1. X(0)=02. X(t)是独⽴平稳增量过程3. X(t)满⾜下列两式:①P{X(t+h)-X(t)=1}=λh+o(h);②P{X(t+h)-X(t)≥2}=o(h);其中o(h)表⽰当h→0时对h的⾼阶⽆穷⼩ 则称X(t)为具有参数λ的泊松过程。