材料力学应力和应变之间的关系
- 格式:ppt
- 大小:533.00 KB
- 文档页数:30

如何理解工程力学中的应力与应变?在工程力学的广袤领域中,应力与应变是两个至关重要的概念。
它们不仅是理解材料力学性能的基石,也是解决众多工程实际问题的关键。
对于初学者来说,这两个概念可能显得有些抽象和难以捉摸,但只要我们耐心剖析,就能发现其中的奥秘。
让我们先来谈谈应力。
应力,简单来说,就是单位面积上所承受的内力。
想象一下,你手里拿着一根橡皮筋,当你用力拉伸它时,橡皮筋内部就会产生抵抗拉伸的力。
如果我们把橡皮筋的横截面积考虑进去,计算出单位面积上的内力,这就是应力。
应力的单位是帕斯卡(Pa),它表示每平方米所承受的力的大小。
在实际的工程应用中,我们常常会遇到不同类型的应力,比如拉伸应力、压缩应力和剪切应力。
拉伸应力出现在材料被拉长的时候,就像刚刚提到的拉伸橡皮筋;压缩应力则相反,发生在材料被压缩的情况下,比如把一根柱子压短;而剪切应力则常见于材料受到平行于其表面的力的作用,例如用剪刀剪断一张纸。
为了更深入地理解应力,我们来考虑一个具体的例子。
假设我们有一根横截面面积为 1 平方厘米的金属杆,我们对它施加一个 100 牛顿的拉力。
那么,这根金属杆所承受的应力就是 100 牛顿除以 00001 平方米(1 平方厘米= 00001 平方米),即 1000000 帕斯卡。
接下来,我们再看看应变。
应变是用来描述物体形状或尺寸变化程度的量。
它是一个无量纲的量,也就是说,它没有单位。
应变可以分为线应变和角应变。
线应变表示物体在某一方向上长度的相对变化。
如果一根原来长度为 L 的杆子,在受到外力作用后长度变成了 L',那么线应变就等于(L' L)/L 。
还是以刚才的金属杆为例,如果它原来的长度是1 米,被拉伸后变成了 101 米,那么线应变就是(101 1)/ 1 = 001 。
角应变则用于描述物体角度的变化。
比如说,一个原本是直角的物体,在受到外力作用后角度发生了改变,这个角度的变化量就是角应变。


应力-应变循环曲线应力-应变循环曲线是材料力学中的重要概念,用来描述材料在循环载荷下的变形行为。
循环载荷是指反复施加在材料上的载荷,应力-应变循环曲线则可用来描述材料在这种交替循环载荷下的应力和应变之间的关系。
本文将详细介绍应力-应变循环曲线的概念、特征和应用。
应力-应变循环曲线通常由两个主要的部分组成:弹性阶段和塑性阶段。
在材料的弹性阶段,应变与应力成正比,即应力和应变满足胡克定律。
材料在这个阶段内,完全恢复了外部加载引起的应变,没有残余应变。
应力-应变曲线在这个阶段呈现出一条直线,斜率代表了材料的弹性模量。
当材料超过了弹性极限,进入了塑性阶段,应力-应变曲线就变成了一个回弹曲线。
在每个循环中,材料会出现一个塑性变形区域,在这个区域内,应变与应力的关系是非线性的。
一般来说,塑性变形区域是由初始的弹性后塑性应变(yield strain)和持续的塑性应变组成。
应力-应变循环曲线的特征还包括屈服点和饱和点。
屈服点是指应力-应变曲线上的一个特殊点,表示了材料的屈服强度。
在屈服点之后,材料会出现明显的应力软化效应,即应力下降。
而饱和点则表示了材料在循环载荷下的最大应变能力。
应力-应变循环曲线的形状和特征会受到多种因素的影响,包括加载速率、温度和材料的微观结构等。
这些因素都会对材料的塑性变形机理和位错运动产生影响。
例如,加载速率的增加会导致材料的强化效应,使得应力-应变曲线呈现出更陡峭的斜率和更高的屈服强度。
而温度的增加则会导致材料的软化效应,使得应力-应变曲线呈现出更平缓的斜率和较低的屈服强度。
应力-应变循环曲线的研究在材料科学和工程领域具有重要的意义。
它不仅可以用来评估材料的力学性能和可靠性,还可以用来设计和优化结构的工作寿命和耐久性。
通过分析应力-应变循环曲线,可以获得材料的弹塑性性质、疲劳特性和损伤行为等信息,有助于提高材料的使用寿命和安全性。
总之,应力-应变循环曲线是描述材料在循环载荷下的力学响应的重要工具。

弹性力学弹性材料的应力应变关系与力学行为弹性力学是研究物体在受力作用下产生的形变,并研究这种形变与施加力之间的关系的力学学科。
弹性材料是指在受到外力作用时,可以恢复其原有形状和大小的材料。
在弹性力学中,应力应变关系是研究弹性材料变形的重要理论基础,同时也是理解弹性材料力学行为的关键。
一、应力应变关系弹性材料的应力应变关系是指在弹性变形过程中,材料受到的应力与应变之间的关系。
根据前人的研究,线弹性模型是描述弹性材料应力应变关系较为简单的模型。
在线弹性模型中,应力与应变之间满足线性的关系,即应力与应变成正比。
线弹性模型的数学表达为:应力=弹性模量×应变其中,弹性模量是描述材料抵抗形变的能力,常用符号为E,单位为帕斯卡(Pa);应变是材料在受力作用下发生的形变,通常用ε表示。
二、力学行为在实际工程中,弹性材料的力学行为可以通过拉伸试验来研究。
拉伸试验是将材料在两端加以拉伸,观察材料的变形与受力之间的关系。
通过拉伸试验可以得到材料的应力-应变曲线,从而了解其力学行为。
应力-应变曲线通常可分为三个阶段:线弹性阶段、屈服阶段和塑性阶段。
1. 线弹性阶段材料在小应变下,应力与应变之间呈线性关系,即遵循线弹性模型。
在这个阶段,材料受力后会发生弹性形变,一旦撤去外力,材料便会恢复到初始状态。
2. 屈服阶段当应力超过材料的屈服强度时,材料开始发生塑性变形。
此时,材料的应变与外力不再成线性关系,应力-应变曲线开始变得非线性。
3. 塑性阶段在超过屈服阶段后,材料会出现塑性变形,即使撤去外力,材料也不能完全恢复到初始状态。
材料在这个阶段会发生永久性变形。
除了拉伸试验,弹性材料的力学行为还可以通过其他实验方法进行研究,如压缩试验和剪切试验等。
通过这些实验,可以探究材料在不同受力情况下的变形特性。
总结:弹性力学中,弹性材料的应力应变关系是研究弹性材料变形的重要理论基础。
应力应变关系可以通过线弹性模型进行描述,其中应力与应变成正比。



材料力学的基本假设
1.应力-应变的线性关系假设:在小变形范围内,材料的应力与应变
之间存在线性关系,即应力是应变的线性函数。
2.同性与各向同性假设:材料在各个方向上具有相同的物理性质,即
同性;在任意方向上的物理性质相同,即各向同性。
3.材料的连续性假设:材料在微观层面上具有连续性,即认为材料是
由无数微小的质点组成的,而且质点之间的距离可以被忽略。
4.材料的弹性本质假设:材料在受力后会发生形变,但当去除作用力时,材料会恢复原始形态,即弹性本质。
5.应力状态的平衡假设:材料在受力时,应力状态必须处于平衡状态,即所受的所有内部力的合力必须为零。
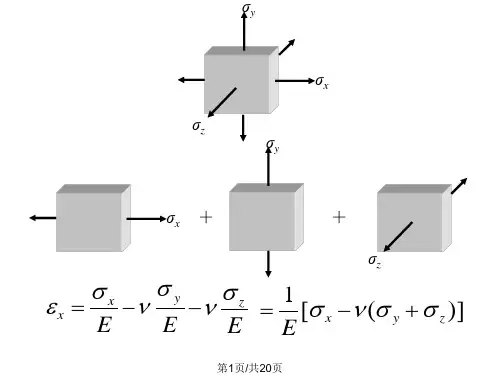
6.多轴应力状态的等效假设:将多轴应力状态转化为等效单轴应力状态,使得应力状态的分析变得简单。
7.破坏准则的假设:材料在受到超过一定程度的应力时会发生破坏,
该程度可以通过破坏准则进行描述。



材料力学应力
材料力学应力是指物体内部受到力的作用下,产生的单位面积内部力的大小,也可以理解为物体内部的拉伸或压缩程度。
它是物体受到外力作用下,内部分子间的相互作用反应的体现,通常用σ表示。
应力是一个标量,其单位通常为帕斯卡(Pa)或兆帕斯卡(MPa),在材料的拉伸或压缩过程中,应力会发生变化,产生不同的应力分布。
常见的应力有:拉应力、压应力、剪应力、扭转应力等。
材料的强度、破断和变形行为都与应力有密切的关系。
材料在应力作用下会发生变形,产生的变形与应力之间有一个关系,即材料的应力-应变关系。
应变是指物体的相对变形量,是单位长度内的形变大小。
应变是材料力学中的一个基本概念,通常用ε表示。
应变也是一个标量,其单位通常为无量纲或毫
米/毫米(mm/mm)。
材料的应力-应变关系通常通过应力-应
变曲线表示,这个曲线可以用来研究材料的力学性质,例如弹性模量、屈服强度、极限强度、延展性等。
在材料科学和结构工程中,应力和应变是非常重要的概念。
工程师和科学家需要了解材料的应力和应变行为,以便设计和预测建筑物、机器、车辆和其他结构的性能。
在工程设计中,应力和应变的考虑是至关重要的,因为结构的强度和稳定性直接取决于它们的力学特性。
这些概念也被用于制造和测试新材料,从而更好地了解材料的性能和用途。
我所认识的应力与应变关系机械与动力工程学院张淑颖612080706053在弹塑性力学中,可变性固体在外力作用下将发生变形。
根据变形的特点,固体在受力过程中的力学行为可分成两个明显不同的阶段:当外力小于某一限值(通常称之为弹性极限荷载)时,在引起变形的外力卸载后固体能完全恢复原来的形状,这种能恢复的变形成为弹性变形,固体只产生弹性变形的阶段成为弹性阶段;外力一旦超过弹性极限荷载,这时再卸除和在,固体也不能恢复原状,其中有部分不能消失的变形被保留下来,这种保留下来的永久变形就成为塑性变形,这一阶段成为塑性阶段。
在弹性阶段,应力和应变之间存在一一对应的单值函数关系,而且还假设是线性关系;在塑性阶段,应力和应变之间通常不存在一一对应的关系,而且通常还是非线性关系(这种非线性成为物理非线性)。
构成实际固体的材料种类很多,它们的性质各有差异,为方便研究,往往根据材料的主要性质做出某些假设,在弹性理论中,有如下的基本假设:⑴假设物体是连续的。
物体内部由连续介质组成,物体中没有空隙,因此物体中的应力、应变、位移等量是连续的,可以用坐标的连续函数表示。
⑵假设物体是均匀的。
整个物体是由同一材料组成的,所有各部分具有相同的弹性,物体弹性常数不随位置坐标而变,可以取出该物体的任意一小部分来加以分析,然后把分析的结果应用于整个物体。
⑶假设物体是各向同性的。
物体的弹性在所有各个方向都相同,物体的弹性常数弹性模量、泊松系数不随方向而变。
显然,木材和竹材的构件都不能当做各向同性体。
至于钢材的构件,虽然含有各向异性的晶体,但由于晶体很微小,而且是随机排列的,因此钢材构件的弹性包含无数多微小晶体随机排列时的统观弹性大致是各向同性的。
⑷假设物体是完全弹性的。
凡是符合以上四个假定的物体,就称为理想弹性体。
⑸假设位移和应变是微小的。
假定物体受力以后,整个物体所有各点的位移都远远小于物体原来的尺寸,并且应变和转角都远小于。
这样,在建立物体变形以后的平衡方程时,就可以用变形以前的尺寸来代替变形以后的尺寸,而不致引起显著的误差。
应力与应变的关系
应力与应变是相互关联的概念,有着密切的关系。
下文将对应力与应变的关系
作详细的解释。
首先,需要了解应力和应变的概念,应力是一种外力对材料的作用,包括张力,剪力,扭转力和摩擦。
应变本质上是材料力学特性的变化,是以体积为例子的变形,受应力的强大影响而形成的。
其次,应力和应变的关系本质上是一种“折中”的关系,材料对某种外力的反
应强度不定;受应力越大,应变就会越大,物体越有可能变形;受应力越小,应变就会越小,这就说明应力和应变之间呈现出正比的关系。
正是基于这种关系,受应力的大小可以通过测量材料的应变来表示,这是测定应力的一种重要方式。
最后,由于应力与应变之间的密切关系,对其进行计算模拟可以有效预测在应
力作用下材料的表现,科学上精确的计算模型可以模拟出完整的应力、应变关系并用于进行预测。
总之,应力与应变之间的关系是相互关联的,相互影响的关系。
它具有很强的
可预测性、可算法化的特点,可以更好地解释材料行为,并且为预测带来很大的方便。
应力和应变1. 简介在力学和材料科学中,应力和应变是两个重要的概念。
应力是指材料内部受到的力的作用,而应变是指材料在受到力作用后发生的形变。
应力和应变是描述材料力学性能的基本参数,对于材料的设计和工程应用具有重要意义。
2. 应力应力是材料内部受到的力的作用,通常用符号σ表示,其单位是帕斯卡(Pa),也可以使用兆帕(MPa)或千兆帕(GPa)。
应力可以分为三类:正应力、剪应力和法向应力。
2.1 正应力正应力是指作用在材料内部的垂直于截面的力,可以通过力除以截面积来计算。
正应力可以进一步分为拉应力和压应力,分别表示拉伸和压缩材料时的应力。
拉应力表示材料受到拉伸作用时的应力,通常以正数表示。
拉应力会使材料发生形变,具有延展性和弹性,可以恢复原状。
压应力表示材料受到压缩作用时的应力,通常以负数表示。
压应力会使材料发生形变,具有收缩性和塑性,并且不易恢复原状。
2.2 剪应力剪应力是指作用在材料内部的平行于截面但方向不同的力,可以通过力除以截面积来计算。
剪应力会使材料发生扭转和剪切形变。
剪应力会产生剪切变形,对应的是材料的剪切模量,可以用于描述材料的硬度和可塑性。
2.3 法向应力法向应力是指作用在材料内部的垂直于截面方向的力,可以通过力除以截面积来计算。
法向应力会使材料发生压缩或拉伸形变。
法向应力的大小和方向取决于施加力的方向和大小,可用于描述材料的稳定性和破坏性。
3. 应变应变是材料在受到力作用后发生的形变,通常用符号ε表示。
应变可以分为线性应变和非线性应变两类。
3.1 线性应变线性应变是指材料在受到小应力作用时,形变与力之间的关系是线性的。
线性应变可以通过材料的弹性模量来描述,弹性模量是材料在小应力作用下恢复原状能力的度量。
3.2 非线性应变非线性应变是指材料在受到大应力作用时,形变与力之间的关系是非线性的。
非线性应变通常发生在超过材料弹性极限时,即材料开始变形并难以恢复原状的阶段。
非线性应变可以引起材料的塑性变形和破坏,对于材料的设计和使用具有重要影响。
应力应变知识介绍在应力应变知识中,应力是指单位面积上的力,它的大小表示材料受到的力的强度。
常见的应力有正应力、切应力等。
正应力指的是垂直于材料截面的力,在力学中常用希腊字母σ表示,单位为帕斯卡(Pa)。
切应力指的是与材料截面平行的力,在力学中常用希腊字母τ表示,单位也是帕斯卡。
应变是指材料在受到外力作用下产生的变形程度,它与应力有着直接的关系。
常见的应变有线性应变、剪切应变等。
线性应变指的是材料在外力作用下产生的长度变化与原始长度之比,通常用拉伸应变表示,单位为米/米或百分比。
剪切应变指的是材料在外力作用下产生的切变角度与材料厚度之比,单位为弧度或度。
应力与应变之间的关系可以用应力-应变曲线表示。
在应力-应变曲线中,通常可以分为弹性变形区、塑性变形区和断裂区。
弹性变形区是指材料受到外力作用后,在去除外力后能够完全恢复原状的变形区域。
塑性变形区是指材料受到外力作用后,在去除外力后不能完全恢复原状的变形区域。
断裂区是指材料在受到极大外力作用下发生破坏的区域。
除了应力与应变之间的关系,应力应变知识还涉及到应力分布、杨氏模量和泊松比等内容。
应力分布指的是材料在受到外力作用后,应力沿着材料各个方向的分布情况。
杨氏模量是材料刚度的度量,表示材料受到外力作用下产生的线性应变与相应应力之间的关系。
泊松比是材料在受到外力作用下产生的横向应变和纵向应变之比,表征了材料在受力时的横向膨胀和纵向收缩程度。
应力应变知识的应用广泛,涉及到材料的工程设计、结构分析和材料改性等方面。
在工程设计中,了解材料的应力应变性能可以帮助工程师选择合适的材料和结构形式,以确保工程的安全性和可靠性。
在结构分析中,通过研究材料的应力应变分布可以评估结构的承载能力和变形情况。
在材料改性中,通过调整材料的组成和处理工艺可以改变材料的应力应变性能,以满足特定的工程需求。
总之,应力应变知识是材料力学中的核心内容,研究材料在受到外力作用下的变形和破坏行为。