当前位置：文档之家 › 二次函数图象(1)

二次函数图象(1)

  • 格式：ppt
  • 大小：927.00 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

2.二次函数图象(1)

2.二次函数图象(1)

练习3、
2图象上有三点： 二次函数y=x
A (2,a), B (1,b), C (0,c)， 求△ABC的面积
练习4、
直线l过A ( 4, 0 ),B ( 0, 4)两点,与 y=ax2交在第一象限于P，若 △AOP的面积为9/2，求此二次函 数解析式。
(4)图象的顶点是哪一点？ 此时函数有最大值还是有最小值？
(5)y随x的变化怎么变化？
(6)你认为抛物线的开口大小是由 什么决定的？
指出下列函数图象所具有的性质
y 23 x y y 7xx y 23 x 8 13
2
22 2 2 2 22
yy x..5x 0 y 22 x y 21 59x y 试，最终为了 中考一场； 一次、两次、三次、四 次……痛苦，最终为了微 笑一次。
二次函数的图 象和性质（1）
议一议
对于二次函数y=ax2的图象，
(1)你能描述图象的形状吗?
(2)你用什么办法确定抛物线的 开口方向？
(3)图象是轴对称图形吗?如果是， 它的对称轴是什么?请你找出几对 对称点．
练习1：
若抛物线y=ax2 (a ≠ 0)过点（-1, 3）。 1.则a的值是 ； 2.对称轴是____开口_____ 3.顶点坐标是____， 4. 抛物线在x轴的_____方 5.增减性是
练习2、
2过点A（-2，-8）。 已知抛物线y=ax
1.求抛物线的函数解析式 2.判断点B（-1，- 4）是否在此抛物 线上。 3.求出此抛物线上纵坐标为-6的点的 坐标。

2.2 浙教版二次函数的图象(1)

2.2 浙教版二次函数的图象(1)
画出下列函数的图象。 画出下列函数的图象。
y = x2
1 y= x
列表 描点 连线
(1) y = 2x2 2 2 (2) y = − x 3
y = −x 2
用光滑曲线连结时要 用光滑曲线连结时要 用光滑曲线连结时要 用光滑曲线连结时要 自左向右顺次连结 用光滑曲线连结时要 用光滑曲线连结时要 用光滑曲线连结时要 用光滑曲线连结时要 自左向右顺次连结 自左向右顺次连结 自左向右顺次连结 自左向右顺次连结 自左向右顺次连结 自左向右顺次连结 自左向右顺次连结
y = x2
1、观察右图， 、观察右图， 并完成填空。 并完成填空。 练习2 2、练习2 3、想一想 练习4 4、练习4
二次函数y=ax2的性质 二次函数 １、顶点坐标与对称轴 ２、位置与开口方向 ３、增减性与极值
y = −x2
抛物线 顶点坐标 对称轴 位置 开口方向 增减性 极值
y=x2
（0，0） ， ） y轴 轴
1、已知抛物线y=ax2经过点 （-2，-8）。 、已知抛物线 经过点A（ ， ）。 （1）求此抛物线的函数解析式； ）求此抛物线的函数解析式； （2）判断点B（-1，- 4）是否在此抛物线上。 ）判断点 （ ， ）是否在此抛物线上。 的点的坐标。 （3）求出此抛物线上纵坐标为 的点的坐标。 ）求出此抛物线上纵坐标为-6的点的坐标 解（1）把（-2，-8）代入 ） ， ）代入y=ax2,得 得 -8=a(-2)2,解出 -2,所求函数解析式为 解出a= 所求函数解析式为 解出 y= -2x2. （2）因为 − 4 ≠ −2( −1) 2 ，所以点B（-1 ，-4） ） 所以点 （ ） 不在此抛物线上。 不在此抛物线上。 （3）由-6=-2x2 ,得x2=3, ） 得 x=± 3 所以纵坐标为-6的点有两个 的点有两个， 所以纵坐标为 的点有两个，它们分别是

6.2二次函数的图象和性质(1)

6.2二次函数的图象和性质(1)

§6.2 二次函数的图象和性质（1）[ 教案]备课时间: 主备人:教学目标:经历探索二次函数y=x2的图象的作法和性质的过程，获得利用图象研究二次函数性质的经验．掌握利用描点法作出y=x2的图象，并能根据图象认识和理解二次函数y=x2的性质．能够作为二次函数y=－x2的图象，并比较它与y=x2图象的异同，初步建立二次函数表达式与图象之间的联系．教学重点:利用描点法作出y=x2的图象过程中，理解掌握二次函数y=x2的性质，这是掌握二次函数y=ax2＋bx＋c（a≠0）的基础，是二次函数图象、表达式及性质认识应用的开始．要注意图象的特点．教学难点:函数图象的画法，及由图象概括出二次函数y=x2性质，它难在由图象概括性质，结合图象记忆性质．教学过程:一、作二次函数y=x2的图象。

二、议一议：1.你能描述图象的形状吗？与同伴交流。

2.图象与x轴有交点吗？如果有，交点的坐标是什么？3.当x<0时，y随着x的增大，y的值如何变化？当x>0时呢？4.当x取什么值时，y的值最小？5.图象是轴对称图形吗？如果是，它的对称轴是什么？请你找出几对对称点，并与同伴交流。

三、y=x2的图象的性质：三、例题：【例1】求出函数y=x＋2与函数y=x2的图象的交点坐标．【例2】已知a＜－1，点（a－1，y1）、（a，y2）、（a＋1，y3）都在函数y=x2的图象上，则（）A．y1＜y2＜y3 B．y1＜y3＜y2 C．y3＜y2＜y1 D．y2＜y1＜y3四、练习1．函数y=x2的顶点坐标为．若点（a，4）在其图象上，则a的值是．2．若点A（3，m）是抛物线y=－x2上一点，则m= ．3．函数y=x2与y=－x2的图象关于对称，也可以认为y=－x2，是函数y=x2的图象绕旋转得到．五：小结1、我们通过观察总结得出二次函数y=ax2的图象的一些性质：①、图象——“抛物线”是轴对称图形；②、与x、y轴交点——（0，0）即原点；③、a 的绝对值越大抛物线开口越大，a ﹥0，开口向上，当x ﹤0时，（对称轴左侧），y 随x 的增大而减小（y 随x 的减小而增大）当x ﹥0时，（对称轴右侧），y 随x 的增大而增大（y 随x 的减小而减小）a ﹤0，开口向下，当x ﹤0时，（对称轴左侧），y 随x 的增大而增大（y 随x 的减小而减小）当x ﹥0时，（对称轴右侧），y 随x 的增大而减小（y 随x 的减小而增大）（2）今天我们通过观察收获不小，其实只要我们在日常生活中勤与观察，勤与思考，你会发现知识无处不在，美无处不在。

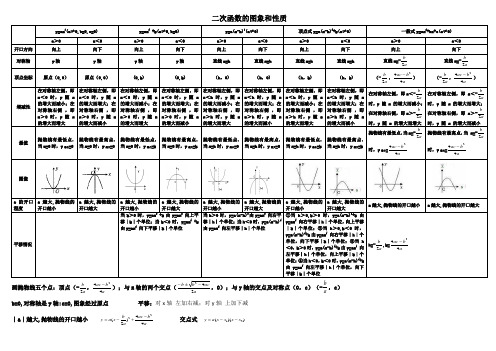
二次函数的图象和性质(含图)

二次函数的图象和性质(含图)

（h，0) 在对称轴左侧，即 x ＜ h 时， y 随 x 的增大而增大；在 对称轴右侧 ，即 x ＞ h 时， y 随 x 的增大而减小
（h，k) 在对称轴左侧，即 x ＜ h 时， y 随 x 的增大而减小；在 对称轴右侧 ，即 x ＞ h 时， y 随 x 的增大而增大
（h，k) 在对称轴左侧，即 x ＜ h 时， y 随 x 的增大而增大；在 对称轴右侧 ，即 x ＞ h 时， y 随 x 的增大而减小
时，y 最小=
4ac b 2 4a
时，y 最大=
4ac b 2 4a
图像
a 的开口 a 越大 , 抛物线的 a 越大 , 抛物线的 a 越大 , 抛物线的 a 越大 , 抛物线的 程度 开口越小 开口越大 开口越小 开口越大 2 2 当 k＞0 时，y=ax +k 由 y=ax 向上平 移∣k∣个单位；当 k＜0 时，y=ax2 +k 由 y=ax2 向下平移∣k∣个单位
a 越大 , 抛物线的 a 越大 , 抛物线的 开口越小 开口越大 2 2 当 h＞0 时，y=a(x-h) 由 y=ax 向右平 移∣h∣个单位；当 h＜0 时，y=a(x-h)2 由 y=ax2 向左平移∣h∣个单位
平移情况
a 越大 , 抛物线的 a 越大 , 抛物线的 a 越大,抛物线的开口越小 开口越小 开口越大 2 ①当 h ＞ 0,k ＞ 0 时， y=a(x-h) +k 由 y=ax2 向右平移∣h∣个单位， 向上平移 ∣ k ∣个单位；②当 h ＞ 0,k ＜ 0 时， 2 2 y=a(x-h) +k 由 y=ax 向右平移∣h∣个 单位，向下平移∣ k ∣个单位；③当 h 4ac b 2 b h=,k= 2 2 ＜0，k＞0 时，y=a(x-h) +k 由 y=ax 向 2a 4a 左平移∣h∣个单位，向上平移∣k∣个 单位； ④当 h＜0， k＜0 时， y=a(x-h)2+k 2 由 y=ax 向左平移∣h∣个单位，向下 平移∣k∣个单位

1.2 二次函数的图象(1)

1.2 二次函数的图象(1)

1.2 二次函数的图象(1)二次函数y=ax 2(a≠0)的图象是顶点在原点的一条抛物线，当a>0时，开口向上；当a<0时，开口向下．1.已知抛物线y=(m-1)x 2经过点(－1，－2)，那么m 的值是(B ).A.1B.－1C.2D.－22.抛物线y=ax 2(a ＜0)的图象一定经过(B ).A.第一、二象限B.第三、四象限C.第一、三象限D.第二、四象限3.函数y=xa 与y=ax 2(a≠0)在同一平面直角坐标系中的图象可能是(D ). A. B.C. D. 4.在同一平面直角坐标系中作函数y=3x 2，y=-3x 2，y=31x 2的图象，这些图象的共同特点是(B ).A.都是关于x 轴对称，抛物线开口向上B.都是关于y 轴对称，抛物线的顶点都是原点C.都是关于原点对称，抛物线的顶点都是原点D.都是关于y 轴对称，抛物线开口向下 5.某车的刹车距离y(m)与开始刹车时的速度x(m/s)之间满足二次函数y=201x 2(x ＞0)，若该车某次的刹车距离为5m ，则刹车前的速度为(C ).A.40m/sB.20m/sC.10m/sD.5m/s 6.已知抛物线y=ax 2(a ＞0)过A(-2，y 1)，B(1，y 2)两点，则下列关系式中,一定正确的是(C ).A.y 1＞0＞y 2B.y 2＞0＞y 1C.y 1＞y 2＞0D.y 2＞y 1＞07.若抛物线y=ax 2经过点A(3，-9)，则其函数表达式为 y=-3x 2 ． 8.若抛物线y=(a+1)x a2+a 开口向下，则a= -2 ．9.已知二次函数y=ax 2的图象经过点P(-2，5).(1)求a 的值.(2)若点M(4，m)在这个二次函数的图象上，求m 的值.【答案（1）∵二次函数y=ax 2的图象经过点P(-2，5)，∴a×(-2)2=5，解得a=45. （2由（1）知二次函数表达式为y=45x 2， ∵点M(4，m)在这个二次函数的图象上，∴m=45×42=20. 10.根据下列条件，求a 的值或取值范围：(1)函数y=(a-2)x 2，当x ＞0时，y 随x 增大而减小;当x ＜0时，y 随x 增大而增大．(2)函数y=(3a-2)x 2有最大值．(3)抛物线y=(a+2)x 2与抛物线y=-21x 2的形状相同． (4)函数y=(a-1)x a2-a 的图象是开口向上的抛物线．【答案】（1）a ＜2．（2）a ＜32． （3）a=-2.5.（4）a=2.11.已知四个二次函数的图象如图所示，则a 1，a 2，a 3，a 4的大小关系是(A ).A.a 1＞a 2＞a 3＞a 4B.a 1＜a 2＜a 3＜a 4C.a 2＞a 1＞a 4＞a 3D.a 2＞a 3＞a 1＞a 4(第11题) (第12题)12.株洲湘江五桥主桥主孔为拱梁钢构组合体系(如图1所示)，小明在五桥观光，发现拱梁的路面部分均匀排列着9根支柱，他回家上网查到了拱梁是抛物线，其跨度为20m ，拱高(中柱)10m ，于是他建立如图2所示的平面直角坐标系，将余下的8根支柱的高度都算出来了.那么，中柱右边第二根支柱的高度是(D ). A.7m B.7.6m C.8m D.8.4m13.边长为1的正方形OABC 的顶点A 在 x 轴正半轴上，点C 在y 轴正半轴上，将正方形OABC 绕顶点O 顺时针旋转75°，如图所示，使点B 恰好落在函数y=ax 2(a ＜0)的图象上，则a 的值为(D ).A.- 2B.-1C.- 423D.- 32 (第13题) (第14题)14.如图所示，边长为2的正方形ABCD 的中心在直角坐标系的原点O 上，AD∥x 轴，以O 为顶点且过A ，D 两点的抛物线与以O 为顶点且过B ，C 两点的抛物线将正方形分割成几部分.则图中阴影部分的面积是 2 ．15.已知函数y=ax 2(a≠0)与直线y=2x-3交于点A(1，b).(1)求a 和b 的值．(2)当x 取何值时，二次函数y=ax 2中的y 随x 的增大而增大？(3)求抛物线y=ax 2与直线y=2x-3的另一个交点B 的坐标．【答案】（1）a=-1,b=-1.（2）∵a=-1，∴二次函数y=ax 2为y=-x 2，它的图象开口向下，对称轴为y 轴. ∴当x ＜0时，y 随x 的增大而增大. （3）解方程组⎩⎨⎧-=-=232x y x y ,得⎩⎨⎧-==1111y x ,⎩⎨⎧-=-=9322y x . ∴抛物线y=ax 2与直线y=2x-3的另一个交点B 的坐标是（-3，-9）．16.有一座横断面为抛物线形状的拱桥，其水面宽AB 为18m ，拱顶O 离水面AB 的距离OM 为8m ，货船在水面以上部分的横断面是矩形CDEF ，建立如图所示的平面直角坐标系．(1)求此抛物线的二次函数表达式．(2)如果限定矩形的长CD 为9m ，那么矩形的高DE 不能超过多少米，才能使船通过拱桥？(3)若设EF=a ，请将矩形CDEF 的面积S 用含a 的代数式表示，并指出a 的取值范围．【答案】（1）y=-818x 2．（2）∵CD=9,∴点E 的横坐标为29，则点E 的纵坐标为-818×⎪⎭⎫ ⎝⎛292=-2. ∴点E 的坐标为（29,-2）. ∴要使货船能通过拱桥，则货船高度不能超过8-2=6（m ）.（3）∵EF=a，∴点E 坐标为（21a,- 812a 2） (第16题) ∴ED=8-│-812a 2∣=8-812a 2. ∴S 矩形CDEF =EF·ED=8a -812a 3（0＜a ＜18）． (第17题)17.如图所示，在平面直角坐标系中，O 为坐标原点，直线y=4x+4交y 轴于点A ，在抛物线y=2x 2上是否存在一点P ，使△POA 的面积等于10？若存在，求出点P 的坐标；若不存在，说明理由．【答案】假设存在一点P （m ，n ），使S △POA =10.∴S=21OA·|m|=10，即21×4×|m|=10， 解得m=5或-5.把m 代入y=2x 2，解得n=50.∴点P 的坐标为（5，50）或（-5，50）．18.【宁夏】已知a≠0，在同一平面直角坐标系中，函数y=ax 与y=ax 2的图象有可能是(C ). A.B. C. D.(第19题) 19.【淄博】如图所示，Rt△OAB 的顶点A(-2，4)在抛物线y=ax 2上，将Rt△OAB 绕点O 顺时针旋转90°，得到△OCD，边CD 与该抛物线相交于点P ，则点P 的坐标为 （2，2） （第20题）20.如图所示，垂直于x 轴的直线AB 分别与抛物线C 1：y=x 2(x ≥0)和抛物线C 2：y= 42x (x ≥0)交于A ，B 两点，过点A 作CD∥x 轴分别与y 轴和抛物线C 2交于点C ，D ，过点B作EF∥x 轴分别与y 轴和抛物线C 1交于点E ，F ，则EADOFB S S ∆∆的值为(D ). A. 62 B. 42 C. 41 D. 61 【解析】设点A ，B 的横坐标为a （a ＞0），则点A 的纵坐标为a 2，点B 的纵坐标为42a ∵BE∥x 轴，∴点F 的纵坐标为42a .∵F 是抛物线y=x 2上的点， ∴点F 的横坐标为x=y =21a. ∵CD∥x 轴，∴点D 的纵坐标为a 2.∵D 是抛物线y=42x 上的点， ∴点D 的横坐标为x=y 4=2a.∴AD=a，BF=21a ，CE=43a 2，OE=41a 2. ∴EAD OFBS S ∆∆=CE AD OE BF ⋅⋅2121=224321412121a a a a ⨯⨯⨯⨯=61.故选D.。

二次函数图像和性质课件(1)完整版公开课

二次函数图像和性质课件(1)完整版公开课
• 一般地, y=a(x-h)²+k(a≠0) 的图象可以看成 y=ax²的图象先沿x轴整体左(右)平移|h|个单位 (当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体 上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移) 得到的.
• 因此,二次函数y=a(x-h)²+k的图象是一条抛物线, 它的开口方向、对称轴和顶点坐标与a,h,k的值 有关.
到
二次函数y=3(x-1)2+2的 图象和抛物线 y=3x²,y=3(x-1)2有什么关 系?它的开口方向,对称轴 和顶点坐标分别是什么?
y 3x 12 2
y 3x 12
二次函数y=3(x-1)2+2的 图象可以看作是抛物线 y=3x2先沿着x轴向右平移 1个单位,再沿直线x=1向 上平移2个单位后得到的.
向下
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
当x=h时,最小值为k.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
当x=h时,最大值为k.
小练习: 抛物线
y 1 x2 2
y 5x2 2
y 2(x 1)2
y (x 1)2 2
向上平移 9 个单位可得到 y=x2+2的图象。
(3)将抛物线y=4x2向上平移3个单位，所得的抛物线的函数 式是 y=4x2+3 。
将抛物线y=-5x2+1向下平移5个单位,所得的抛物线的函 数式是 y=-5x2-4 。
回顾:
(1)怎样的抛物线可以通过平移得到? 二次项系数a值相同的抛物线可以通过平移得到
X=1
对称轴仍是平行于y轴的直 线(x=1);增减性与y=3x2类似.

2.2 二次函数的图象(1)课件1


例1、已知二次函数 、已知二次函数y=ax2(a≠0)的图 的图 像经过点(-2,-3). 像经过点 的值， (1)求a的值，并写出这个二次函数的解析式 的值 并写出这个二次函数的解析式. (2)说出这个二次函数的顶点坐标、对称轴、开 说出这个二次函数的顶点坐标、对称轴、
口方向和图像的位置. 口方向和图像的位置
y = x2
列表
画出下列函数的图象。 画出下列函数的图象。
描点 连线
1 2 (1) y = x 2 (2) y = 2x2 2 2 (3) y = − x 3
y = −x 2 用光滑曲线连结时要 自左向右顺次连结
x
y= 1 2 x y=x2 2
... ... ... ... ... ...
Байду номын сангаас
-3 4.5 -1.5 4.5
义务教育课程标准实验教科书 浙教版九年级上册
回顾知识: 回顾知识:
一、一次函数y=kx+b（k ≠ 0）的图象是什么？ 一次函数 （ ）的图象是什么？ 图象是一条直线. 图象是一条直线
k 0）的图象是什么？ 二、反比例函数 y = （k ≠ 0）的图象是什么？ x
图象是双曲线. 图象是双曲线
二次函数y=ax²+ bx+c（a ≠ 0） 二次函数 （ ） 其图象又是什么呢？ 其图象又是什么呢？
2 y = − x2 在x轴的 （2）抛物线 ） 轴的 3
除顶点外）， ），在对称轴的 下 方（除顶点外），在对称轴的
左侧， 随着 随着x的 在对称轴的右侧， 随着 随着x的 左侧，y随着 的 增大而增大 ；在对称轴的右侧，y随着 的 增大而减小 ，当x=0时，函数 的值最大，最大值是 的值最大， 时 函数y的值最大 0 ，

课件1二次函数的图像和性质


（2）在平面直角坐标系中描点：
y
-4
-3
-2
-1
o
1
2
3
4
x
-2
-4
-6
-8
y = - x2
-10
（3）用光滑曲线顺次连接各点，便得到函数y= -x2 的图象.
二次函数的图象是不是跟投篮路线很像？
知识要点
抛物线： 像这样的曲线通常叫做抛物线。 二次函数的图象都是抛物线。
一般地，二次函数 y ax2 bx c 的图象叫做抛物线 y ax2 bx c。
()
A．江南制造总局的汽车
B．洋人发明的火车
C．轮船招商局的轮船
D．福州船政局的军舰
[解析] 由材料信息“19世纪七十年代，由江苏沿江居民 到上海”可判断最有可能是轮船招商局的轮船。
二、近代以来交通、通讯工具的进步对人们社会生活的影 响
(1)交通工具和交通事业的发展，不仅推动各地经济文化交 流和发展，而且也促进信息的传播，开阔人们的视野，加快 生活的节奏，对人们的社会生活产生了深刻影响。
(2)通讯工具的变迁和电讯事业的发展，使信息的传递变得 快捷简便，深刻地改变着人们的思想观念，影响着人们的社 会生活。
y= 2x2
y=x2
y 10
9 8 7 6 5 4
3 2 1
y= 0.5x2
-5 -4 -3 -2 -1 o 1 2 3 4 5 x
y 1
-5 -4 -3 -2 -1-1 o 1 2 3 4 5 x -2
-3 -4
-5
-6
-7
-8 -9
y=－21 x
-10
y=－2x2 y=x2
a的符号决定抛物线的开口方向，|a|的 大小决定抛物线开口的大小，|a|越大开 口越小

6.2二次函数的图象和性质(1)

§6.2 二次函数的图象和性质（1）备课时间: 主备人:教学目标:经历探索二次函数y=x2的图象的作法和性质的过程，获得利用图象研究二次函数性质的经验．掌握利用描点法作出y=x2的图象，并能根据图象认识和理解二次函数y=x2的性质．能够作为二次函数y=－x2的图象，并比较它与y=x2图象的异同，初步建立二次函数表达式与图象之间的联系．教学重点:利用描点法作出y=x2的图象过程中，理解掌握二次函数y=x2的性质，这是掌握二次函数y=ax2＋bx＋c（a≠0）的基础，是二次函数图象、表达式及性质认识应用的开始．要注意图象的特点．教学难点:函数图象的画法，及由图象概括出二次函数y=x2性质，它难在由图象概括性质，结合图象记忆性质．教学过程:一、作二次函数y=x2的图象。

二、议一议：1.你能描述图象的形状吗？与同伴交流。

2.图象与x轴有交点吗？如果有，交点的坐标是什么？3.当x<0时，y随着x的增大，y的值如何变化？当x>0时呢？4.当x取什么值时，y的值最小？5.图象是轴对称图形吗？如果是，它的对称轴是什么？请你找出几对对称点，并与同伴交流。

三、y=x2的图象的性质：三、例题：【例1】求出函数y=x＋2与函数y=x2的图象的交点坐标．【例2】已知a＜－1，点（a－1，y1）、（a，y2）、（a＋1，y3）都在函数y=x2的图象上，则（）A．y1＜y2＜y3 B．y1＜y3＜y2 C．y3＜y2＜y1 D．y2＜y1＜y3四、练习1．函数y=x2的顶点坐标为．若点（a，4）在其图象上，则a的值是．2．若点A（3，m）是抛物线y=－x2上一点，则m= ．3．函数y=x2与y=－x2的图象关于对称，也可以认为y=－x2，是函数y=x2的图象绕旋转得到．五：小结1、我们通过观察总结得出二次函数y=ax2的图象的一些性质：①、图象——“抛物线”是轴对称图形；②、与x、y轴交点——（0，0）即原点；③、a 的绝对值越大抛物线开口越大，a ﹥0，开口向上，当x ﹤0时，（对称轴左侧），y 随x 的增大而减小（y 随x 的减小而增大）当x ﹥0时，（对称轴右侧），y 随x 的增大而增大（y 随x 的减小而减小）a ﹤0，开口向下，当x ﹤0时，（对称轴左侧），y 随x 的增大而增大（y 随x 的减小而减小）当x ﹥0时，（对称轴右侧），y 随x 的增大而减小（y 随x 的减小而增大）（2）今天我们通过观察收获不小，其实只要我们在日常生活中勤与观察，勤与思考，你会发现知识无处不在，美无处不在。

第1讲二次函数的图象和性质复习课件(共39张PPT)

全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
第二种是在瑞典本国流行的说法．在诺贝尔立遗嘱期 间，瑞典最有名望的数学家就是米塔格·勒弗列尔，诺贝尔 很明白，如果设立数学奖，这项奖金在当时必然会授予这位 数学家，而诺贝尔很不喜欢他．所以诺贝尔不设立数学奖．
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
从函数图象中获取信息 a的作用：决定开口的方向和大小． (1)a＞0开口向上，a＜0开口向下； (2)a越大，抛物线的开口越小． b的作用：决定顶点的位置． 左(对称轴在y轴左边) 同(a，b同号) 右(对称轴在y轴右边) 异(a，b异号) c的作用：决定抛物线与y轴交点的位置． 上(抛物线与y轴的交点在y轴正半轴)
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
【解析】 ①∵图象与x轴的交点A，B的横坐标分别为－1，3， ∴AB＝4， ∴对称轴 x＝－2ba＝1， 即2a＋b＝0， 故①错误； ②根据图示可知，当x＝1时，y＜0，即a＋b＋c＜0， 故②错误； ③∵点A的坐标为(－1，0)， ∴a－b＋c＝0，且b＝－2a， ∴a＋2a＋c＝0，即c＝－3a， 故③正确；
大师导航 归类探究 自主招生交流平台 思维训练
第一章 二次函数
第1讲 二次函数的图象和性质
全效优等生
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
诺贝尔为什么没有设数学奖 诺贝尔奖在全世界有很高的地位，许多科学家梦想着能 获得诺贝尔奖．数学被誉为“科学女皇的骑士”却得不到每年由 瑞典科学院颁发的诺贝尔奖，过去没有，将来也不会有．因为 瑞典著名化学家诺贝尔留下的遗嘱中没有提出设立数学奖．对 此，外界流传着两种说法． 第一种是在法国和美国流行的说法．与诺贝尔同时期的 瑞典著名数学家米塔格·勒弗列尔曾是俄国彼得堡科学院的外 籍院士，后来又是前苏联科学院的外籍院士．米塔格·勒弗列 尔曾侵犯过诺贝尔的夫人，诺贝尔对他非常厌恶．为了对他所 从事的数学研究进行报复，所以诺贝尔不设立数学奖．
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

?
做一做
函数y=a(x-h)2(a≠0)的图象和性质
在同一坐标系中作Βιβλιοθήκη 二次函数y=3x2,y=3(x-1)2和 y=3(x+1)2的图象． 完成下表,并比较3x2,3(x-1)2和3(x+1)2的值, 它们之间有什么关系?
x -4 -3 -2 -1 0 1 2 3 4
y 3x 2
y 3x 1 y 3x 1
x -3 -2 -1 0 1 2 3 4
3 x2
27
12 27
3 12
0 3
3 0
12 3
27 12
48 27
3(x-1)2 48
(2)在同一坐标系中作出二次函数 y=3x2和 y=3(x-1)2的图象．
做一做
y=3x2 (3)函数y=3(x-1)2的 图象与 y =3 x 2 的图象 有什么关系 ? 它是轴 对称图形吗 ? 它的对 称轴和顶点坐标分别 是什么?
?
二次函数y=3(x-1)2+2的
图象和抛物线y=3x² , y=3(x-1)2有什么关系?它 的开口方向、对称轴和 顶点坐标分别是什么?
y 3x 2
y 3x 1 2
2
y 3x 1
2
二次函数y=3(x-1)2+2 的图象可以看作是抛 x=1 物线y=3x2先沿着x轴向 开口向上 右平移1个单位,再沿直 对称轴仍是平行于 y轴的直 ,当 x=1 时有最小 线x=1向上平移2个单 线x=1;增减性与y=3 x2 类似. 值,且最小值为2. 位后得到的. 顶点是(1,2).
独立 作业
知识的升华
P48 习题2.4
1题.
祝你成功！
2.(1)二次函数y=3(x+1)2的图象与二次函数y=3x2的图象有什 么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什 么? (2)二次函数y=-3(x-2)2+4的图象与二次函数y=-3x2的图象有 什么关系? (3)对于二次函数y=3(x+1)2,当x取哪些值时,y的值随x值的增 大而增大?当x取哪些值时,y的值随x值的增大而减小?二次函 数y=3(x+1)2+4呢?
二次函数y=a(x-h)2+k的图象和性质
１.顶点坐标与对称轴
２.位置与开口方向
３.增减性与最值
抛物线
y=a(x-h)2+k(a>0)
（ h，k） 直线x=h
由h和k的符号确定
y=a(x-h)2+k(a<0)
（h，k） 直线x=h
由h和k的符号确定
顶点坐标
对称轴 位置 开口方向
向上
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
2. x取哪些值时,函数 y=3(x+1)2的值随x值的增 大而增大?x取哪些值时, 函数y=3(x+1)2的值随x的 增大而减少？
y 3x 1
y 3x 2
2
y 3x 1
2
在对称轴(直线x=-1)左侧 在对称轴(直线x=-1) 顶点是最低点 ,函数 (即x<-1时),函数y =3(x+1)2 右侧 有最小值 , (即x>-1时), 的值随x的增大而减少 . .当x=-1时 最小值是0. 函数y=3(x+1)2的值 二次函数y=3(x+1)2 随x的增大而增大. 与y=3x2的增减性类似. 猜一猜:函数y=-3(x-1)2,y=-3(x+1)2 和y=-3x2的图象的位置和形状. 请你总结二次函数y=a(x-h)2的图象和性质.
2 2
27
12
3
0
3
12
27
27 27 12 3
12 0
3 3
0 12
3 27
12
27
1. 函数 y =3( x +1) 2 的图象 y 3x 2 2 与y=3x2和y=3(x-1)2的图象 2 y 3 x 1 y 3x 1 有什么关系?它是轴对称图 形吗?它的对称轴和顶点坐 标分别是什么? 二次函数y=3(x+1)2 与y=3x2的图象形状 相同,可以看作是抛 图象是轴对称图形, 二次项系数相同 2 物线y=3x 整体沿x 对称轴是平行于 a>0,开口都向上. 轴向左平移了1 个 y轴的直线:x= -1. 顶点坐标 单位. 是点(-1,0). 2 想一想,二次函数y=3(x+1) 的图象的增减性会怎样?
y=ax2+bx+c
想一想
函数y=ax²+bx +c的图象
二次函数 y=3(x-1)2+2 的图象是什么形状?它与我们已 经作过的二次函数的图象有什么关系?
在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象。
比较二次函数y=3x2和y=3(x-1)2的图象。
⑴完成下表,并比较3x2和3(x-1)2的值,它们之间 有什么关系?
向下
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
增减性 最值
当x=h时,最小值为k.
当x=h时,最大值为k.
随堂练习

悟出真谛,练出本事
2
1.指出下列函数图象的开口方向、对称轴和顶点坐标:
1 1 2 1y 2x 3 ; 2y x 1 5. 3 2
二次函数y=a(x-h)2的性质
１.顶点坐标与对称轴 ２.位置与开口方向 ３.增减性与最值
抛物线 顶点坐标 对称轴
y=a(x-h)2 (a>0)
（h，0） 直线x=h 在x轴的上方(除顶点外) 向上
在对称轴的左侧,y随着x的增大 而减小. 在对称轴的右侧, y随 着x的增大而增大.
y=a(x-h)2 (a<0)
二次项系数 相同a>0, 开口都向上.
想一想,在同一坐标系中作二次函数y=3(x+1)2 的图象,会在什么位置?
(4)x取哪些值时,函数 y=3(x-1)2的值随x值的增 大而增大?x取哪些值时, 函数y=3(x-1)2的值随x的 增大而减少？
y 3x
2
y 3x 1
2
二次函数y=3(x-1)2 有最小值.当x=1时, 在对称轴 (直线x=1)右侧 与y=3x2的增减性类似. 最小值是 0。 (即x>1时),函数y=3(x-1)2 的值随x的增大而增大,. 想一想,在同一坐标系中作出二次函数

小结
拓展
二次函数y=a(x-h)² +k与y=ax² 的关系
1.相同点: (1)形状相同(图象都是抛物线,开口方向相同). (2)都是轴对称图形. (3)都有最(大或小)值. (4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称 轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y 都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 . 2.不同点: 只是位置不同(1)顶点不同:分别是(h,k)和(0,0). (2)对称轴不同:分别是直线x= h和y轴. (3)最值不同:分别是k和0. 3.联系: y=a(x-h)² +k(a≠0) 的图象可以看成y=ax² 的图象先沿x轴整 体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再 沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向 下平移)得到的.
二次函数y=a(x-h)² +k与y=ax² 的关系

一般地,由y=ax²的图象便可得到二次函数 y=a(x-h)²+k的图象:y=a(x-h)²+k(a≠0) 的图象可以看成y=ax²的图象先沿x轴整体 左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下) 平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的. 因此,二次函数y=a(x-h)² +k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与 a,h,k的值有关.
y=3(x-1)2
(4)x取哪些值时,函数y=3(x-1)2的值随x值的增大 而增大?x取哪些值时,函数y=3(x-1)2的值随x的 增大而减少？
(3)函数y=3(x-1)2的图象 与 y =3 x 2 的图象有什么关 系?它是轴对称图形吗?它 的对称轴和顶点坐标分别 是什么?
y=3x2
二次函数y=3(x-1)2 图象是轴对称图形, 与y=3x2的图象形状 对称轴是平行于 相同,可以看作是抛 y轴的直线:x=1. 物线y=3x2整体沿x轴 顶点坐标 向右平移了1 个单位. 是点(1,0).
（h，0） 直线x=h 在x轴的下方( 除顶点外) 向下
在对称轴的左侧,y随着x的增大 而增大. 在对称轴的右侧, y随 着x的增大而减小.
位置
开口方向 增减性 最值
开口大小
当x=h时,最小值为0.
a 越大,开口越小.
当x=h时,最大值为0.
a 越小,开口越大.
做一做
我思，我进步
在同一坐标系中作出二次函数y=3x² ,y=3(x-1)2和 y=3(x-1)2+2的图象. 二次函数y=3x² ,y=3(x-1)2和y=3(x-1)2+2的图象有什么 关系?它们的开口方向、对称轴和顶点坐标分别是什么 ? 作图看一看．
二次函数y=-3(x-1)2,y=-3(x+1)2和y=-3x2的图象
y 2.抛物线y=-3(x-1)2 和y=-3(x+1)2在x轴的 下方(除顶点外),它的 2 2 开口向下,并且向下无 y 3x 1 y 3x 1 限伸展. 1.抛物线y=-3(x-1)2 3.抛物线y=-3(x-1)2在对称轴 的顶点是(1,0);对称 (直线x=1)的左侧(即当x<1时), y =1;抛物线 y 3x 2 轴是直线x2 随着x的增大而增大;在对称轴 y=-3(x+1) 的顶点是 (直线x=1)右侧(即当x>1时), y随 x=-1 x=1 (-1,0);对称轴是直线 着x的增大而减小;当x=1时,函 x=-1. 数y的值最大(是0).抛物线y=4.抛物线y=-3(x-1)2可以看作是 3(x+1)2在对称轴(直线x=-1)的 抛物线y=-3x2沿x轴向右平移了1 左侧(即当x<-1时), y随着x的增 个单位;抛物线y=-3(x+1)2可以看 大而增大;在对称轴(直线x=-1) 作是抛物线y=-3x2沿x轴向左平移 右侧(即当x>-1时), y随着x的增 了1个单位. 大而减小;当x=-1时,函数y的值 最大(是0).