闭合导线的连接角观测与平差

闭合导线角度闭合差公式在测量角度闭合差时，一般需要进行多次测量，然后根据实际测量结果计算角度闭合误差。

角度闭合误差是指在闭合导线测量过程中，所测得的角度总和与理论值之间的差异。

这个差异可能由于测量仪器的误差、观测者的操作误差、测量环境的不稳定性等因素导致。

角度闭合差公式的推导涉及到平差理论中的一些基本概念和原则。

其中最为关键的概念是“观测角”，即指测量角度的观测值。

如果设有n个导线闭合，每个导线上都有2个观测角，那么总共会有2n个观测角。

根据平差理论，测得的每个观测角应与理论值之间的差异，记为观测角公差。

设第i个导线的观测角公差为δθi，则总的角度闭合公差可以表示为：Σδθi=0这就是角度闭合公差的基本表达式。

在实际测量中，角度闭合误差通常不可能为零，因此需要进行平差处理。

平差处理的目标是通过调整观测角公差，使得总的角度闭合误差最小。

根据最小二乘法，可以得到平差观测角公差的解析解：δθi=(Σδθi)/n该公式可用于计算每个导线上观测角的平差值。

在应用角度闭合差公式进行实际测量时，还需要考虑其他因素的影响。

例如，导线长度的测量误差、观测角的精度等都会对角度闭合误差产生一定的影响。

此外，如果存在闭合导线中间有障碍物或者地形不平坦的情况，也会导致角度闭合误差的增大，需要进行相应的修正。

在实际测量中，为了减小角度闭合误差，通常会采用以下方法：1.增加测量观测次数，减小观测误差的影响；2.根据测量精度要求，选择合适的观测仪器；3.合理规划导线的测量路线，避免不必要的测量误差；4.进行后方交会检查，找出测量数据中存在的问题，并进行合理修正。

总结起来，闭合导线角度闭合差公式是测量工程中非常重要的一种公式，它可以帮助测量人员对测量数据进行角度平差处理，减小角度闭合误差，提高测量结果的准确性和可靠性。

在实际应用中，需要考虑各种因素的影响，并结合实际情况进行调整和修正，才能得到准确的测量结果。

全站仪测量闭合导线如何平差计算出各点坐标测量闭合导线的平差计算，一般可以分为以下几个步骤：
1.测量闭合导线的原始数据获取：首先，需要在各个测站上用全站仪
测量闭合导线的各个点的水平角和垂直角，并记录下来。

同时，还要测量
闭合导线的距离。

2.计算展点坐标的预计值：根据测量的数据和已知的初始点的坐标，
可以利用三角函数计算出闭合导线上各点的预计坐标值。

在计算中要注意
角度的单位和相应的角度公式。

3.闭合导线的平差计算：根据各点的预计坐标值和测量的实际坐标值，可以进行闭合导线的平差计算。

平差计算的目的是为了得出最接近实测值
的各点坐标。

平差计算的方法有很多种，其中常用的有“角度平差法”和“坐标平
差法”。

以“角度平差法”为例，其步骤如下：
1.计算闭合导线的总角度差：根据测量得到的各个点的角度值，可以
求得闭合导线的总角度差，即闭合差。

2.计算方位角的改正数：根据闭合差和导线的总长度可以计算出方位
角的改正数。

方位角的改正数是为了使计算后的闭合导线与实际测量中的
闭合导线相吻合。

3.计算各点坐标的改正数：根据预计坐标值和实际测量值的差异，可
以计算出各个点的坐标改正数。

4.修正各点坐标：根据上述计算得到的改正数，可以对各点的预计坐标值进行修正，得到最终的各点坐标。

总之，全站仪测量闭合导线的平差计算是一个较为复杂的过程，需要通过测量数据和数学方法进行计算。

只有进行准确的测量和精确的计算，才能得到符合实际情况的各点坐标值。

在平差计算过程中要注意各个环节的精度控制和数据处理，以确保测量结果的准确性和可靠性。

闭合导线坐标计算闭合导线计算式根据外业观测的边长、夹角和方位角以及其中一个导线点的坐标，结合平差计算，来推算其余各导线点的坐标。

设对闭合导线n个内角分别进行了观测，各个符号精度要求的观测值为，并对闭合多边形的n个边长分别进行了测量，各个符号精度要求的观测值为；其中一个导线点的坐标为；确定其余各个导线点的坐标x,1 角度闭合差的计算也调整（1）实测角度闭合差的计算闭合导线n个实测内角的和不等于其理论值（n-2）*180,其差称为角度闭合差以表示：(2)实测角度闭合差检核角度闭合差校核是将实测角度闭合差也同级导线角度闭合差的容许值，按各级导线测量主要技术要求比较，以确定角度综合限差是否满足要求。

这里角度综合限差采用图根导线数据，即=40。

（3）角度闭合差的调整若≤，则可以进行角度闭合的调整，否则，应分析情况重测。

角度闭合差的调整原则是，将以相反的符号平均分配到各个观测角中，即各点改正数为式=／n计算时，根据角度的取位的要求，改正数可凑整到1″、6″、10″.若不能均分，一般情况下，因短边角引起的误差较大，因此给短边角的夹角多分配一点，使各角改正数的总和也反号的闭合差相等，即2、推算各边的坐标方位角推算各边的坐标方位角目的是为了计算坐标增量。

推算方法根据起始方位角及改正后的转折角，按式依次推算出各边的坐标方位角。

或式中：----------第i条边的正方位角---------第i+1条的正方位角--------分别为第i-1条边与第i条边间所夹的左右角。

在推算过程中，如果算出＞360°，则应减去360°如果算出的＜0°，则应加上360°为了发现推算过程中的差错，最后必须推算至起始边的坐标方位角，看其是否与已知值相等，以此作为计算校核。

3 坐标增量闭合差的计算和调整（1）计算实测各边的坐标增量设第i条实测边的终、横坐标增量分别为(2)确定理论纵、横坐标增量∑△Xi理、∑△Yi理闭合导线的纵横坐标增量总和的理论值应为零，则有∑△Xi理=0∑△Yi理=0(3)计算坐标增量闭合差fx.fy由于测量误差，改正后的角度仍有残余误差，坐标增量总和的测量计算值∑△X测与∑△Y测一般都不为零，其值称为坐标增量闭合差，fx.fy表示，则fx=∑△Xi测-∑△Xi理=∑△Xi测fy=∑△Yi测-∑△Yi理=∑△Yi测（4）计算导线全长闭合差f并检核全长相对闭合差K因计算的闭合导线并不闭合，而存在一个缺口，这个缺口的长度称为导线闭合差f导线越长，全长闭合差也越大。

坐标平差闭合计算公式一、坐标平差闭合差计算的基本概念。

1. 定义。

- 在测量工作中，由于观测值存在误差，使得由观测值计算得到的结果（如闭合导线的坐标计算）与理论值之间存在差异，这个差异就称为闭合差。

坐标平差闭合差计算是测量平差中的重要内容，其目的是通过一定的方法对观测值进行调整，使得调整后的结果满足理论上的几何关系。

2. 闭合导线坐标计算中的闭合差类型。

- 角度闭合差：对于闭合导线，其内角和理论值根据多边形内角和公式(n - 2)×180^∘（n为多边形边数）计算。

而实际观测的内角和与理论值之间的差值就是角度闭合差f_β，即f_β=∑limits_i = 1^nβ_i-(n - 2)×180^∘。

- 坐标增量闭合差。

- 在平面直角坐标系中，闭合导线各边坐标增量的代数和在理论上应该为零。

设Δ x_i和Δ y_i分别为第i边的纵、横坐标增量，对于闭合导线，∑limits_i =1^nΔ x_i=0，∑limits_i = 1^nΔ y_i=0。

但由于观测误差的存在，实际计算得到的坐标增量代数和∑limits_i = 1^nΔ x_i=f_x，∑limits_i = 1^nΔ y_i=f_y，f_x和f_y分别称为纵、横坐标增量闭合差。

- 坐标增量闭合差的大小反映了观测误差对坐标计算的影响程度。

根据坐标增量闭合差可以计算出导线全长闭合差f_D，f_D=√(f_x)^2+f_{y^2}。

- 为了衡量导线测量的精度，还需要计算导线全长相对闭合差K=frac{f_D}{∑limits_i = 1^nD_i}（其中∑limits_i = 1^nD_i为导线的总长度）。

二、坐标平差闭合差的调整原则和方法。

1. 角度闭合差的调整。

- 调整原则：将角度闭合差反号平均分配到各观测角中。

设角度闭合差为f_β，观测角个数为n，则每个角的改正数v_β=-frac{f_β}{n}。

- 调整后的角度计算：调整后的角度β_i'=β_i+v_β。

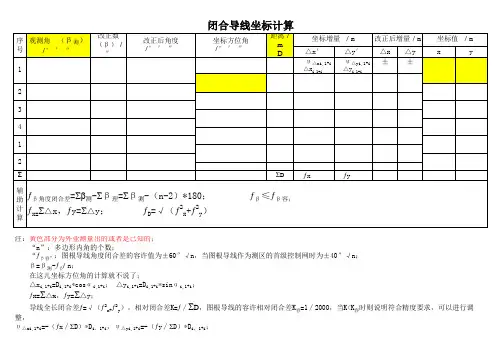
闭合导线坐标计算
注：黄色部分为外业测量出的或者是已知的；
“n”：多边形内角的个数；
“ƒβ容”：图根导线角度闭合差的容许值为±60″√n，当图根导线作为测区的首级控制网时为±40″√n；
β=β测-ƒβ n；
在这儿坐标方位角的计算就不说了；
△x i,1+i=D i,1+i*cosαi,1+i； △y i,1+i=D i,1+i*sinαi,1+i；
ƒx=Ʃ△x，ƒy=Ʃ△y；
导线全长闭合差ƒ=√（ƒ2x+ƒ2y），相对闭合差K=ƒ∕ƩD，图根导线的容许相对闭合差K容=1∕2000，当K<K容时则说明符合精度要求，可以进行调整，
υ△xi,1+i=-（ƒx∕ƩD）*D i，1+i，υ△yi,1+i=-（ƒy∕ƩD）*D i，1+i；
△x △y x y
υ△xi,1+i υ△yi,1+i ±±
△x i,1+i
△y i,1+i
Ʃ
ƩD ƒx ƒy
辅助计算
观测角 （β测） ′ ″改正数
（β） 改正后角度 ′ ″
坐标方位角 ′ ″
56序号1234△x′△y′ƒβ角度闭合差=Ʃβ测-Ʃβ
理=Ʃβ测-（n-2）*180； ƒβ
≤ƒβ容；
ƒx=Ʃ△x，ƒy=Ʃ△y； ƒD =√（ƒ2x +ƒ2y ）
注：1、附合导线和闭合导线的差别在于两个方面：①角度闭合差的计算和调整，②坐标增量闭合差的计算；（怎么计算就不一一说了，见谅！）
坐标增量 m 改正后增量 m
坐标值 m 距离 m。

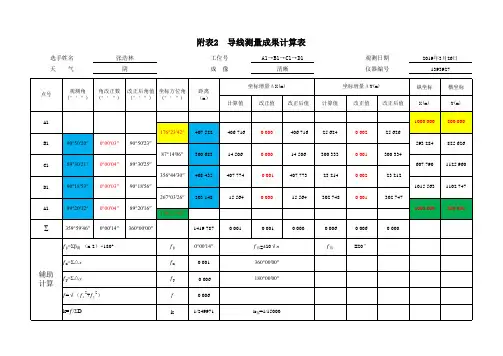
观测日期工位号A1→B1→C1→D1
成 像
清晰
阴
附表2 导线测量成果计算表
2019年3月26日仪器编号
1393927选手姓名天 气
张浩林
说明：本表中n表示闭合环的边数，本表四边形为例，即理论内角和为360°，本表中蓝色底纹部分为链接附件1观测手簿中平均结果数据，黄色底纹为已知数据，绿色底纹为校核数据，红色字体为手动输入数据。

角度改正数分配原则：正常为按边长的比例分配，特殊情况为长边少分，短边多分；坐标增量改正数分配原则：正常为按边长的比例分配，特殊情况为长边多分，短边少分。

随着全站仪在工程测量中应用的逐渐普及，采用导线作为测量的平面控制越来越广泛，导线一般多布设成单一导线。

应用全站仪观测导线，可以通过机内的微处理器，直接得到地面点的平面近似坐标，因此在成果处理时可以应用这些近似坐标直接按坐标平差（即间接平差）法进行平差。

本文主要针对采用全站仪观测导线的近似平差和严密平差方法进行探讨。

导线的近似坐标平差导线测量用于图根控制等低精度测量中，往往采用近似平差即可。

由于全站仪直接测定各导线点的近似坐标值，平差计算就不用像传统的导线近似平差计算那样，先进行角度闭合差计算和调整，然后推算方位角，再进行坐标增量闭合差的计算和调整，最后根据平差后的坐标增量计算导线点的坐标。

全站仪观测导线直接按坐标平差计算，将更为简便。

直接按坐标平差法计算步骤如下：假设有一条附合导线，由于存在观测误差，最后测得的一点（假设为C）坐标与该点已知坐标（xc，yc）不一致，其差值即为纵、横坐标增量闭合差，即（1）导线全长闭合差为f：（2）导线全长相对闭合差为：（3）此时若满足要求的精度，就可以直接根据坐标增量闭合差来计算各个导线点的坐标改正数，各导线点的坐标改正值计算公式为：（4）改正后各点坐标xi、yi为：（5）式中，∆x1、∆x2、∆x i、∆y1、∆y2、∆y i、分别为第一、第二和第i条边的近似坐标增量；x i’、y i’为各待定点坐标的观测值（即全站仪外业直接观测的导线点的坐标）。

采用坐标法进行导线近似平差，直接在已经测得导线点的坐标上进行改正，方法简单，易于掌握，避免了传统近似平差法的方位角的推算和改正，以及坐标增量的计算和改正，能大大提高工作效率，而且不易出错。

同时可以看出传统附和导线测量需要两条已知边，作为方位角的检核条件，而直接坐标法，只需要一条已知边和一个已知点即可，使导线的布网更加灵活。

导线的严密坐标平差采用全站仪观测导线的优势高等级平面控制测量对精度的要求较高，需要严密平差。

全站仪观测的导线采用严密坐标平差法较为适宜。

闭合导线平差计算步骤：1、绘制计算草图。

在图上填写已知数据和观测数据。

2、角度闭合差的计算与调整（1）计算闭合差：（2）计算限差：（图根级）（3）若在限差内，则按平均分配原则，计算改正数：（4）计算改正后新的角值：3、按新的角值，推算各边坐标方位角。

4、按坐标正算公式，计算各边坐标增量。

5、坐标增量闭合差的计算与调整（1）计算坐标增量闭合差。

有：导线全长闭合差：导线全长相对闭合差:（2）分配坐标增量闭合差若 K&lt;1/2000 （图根级），则将、以相反符号，按边长成正比分配到各坐标增量上去。

并计算改正后的坐标增量。

6、坐标计算根据起始点的已知坐标和经改正的新的坐标增量，来依次计算各导线点的坐标。

[ 例题 ] 如图所示闭合导线，试计算各导线点的坐标。

计算表格见下图：闭合水准路线内业计算的步骤：(1) 填写观测数据(2) 计算高差闭合差h f =∑h ，若h f ≤容h f时，说明符合精度要求，可以进行高差闭合差的调整；否则，将重新进行观测。

(3) 调整高差闭合差 各段高差改正数：i hi i hi L L f V n nf V ·· ∑-=∑-=或各段改正高差：ii i V h h +=改(4) 计算待定点的高程闭合差(ｆh )水准路线中各点间高差的代数和应等于两已知水准点间的高差。

若不等两者之差称为闭合差高差闭合差的计算.支水准路线闭合差的计算方法.附合水准路线闭合差的计算方法.闭合水准路线闭合差的计算方法高差闭合差容许值 （n 为测站数，适合山地）(L 为测段长度，以公里为单位，适合平地)水准测量中，消除闭合差的原则一般按距离或测站数成正比地改正各段的观测高差改正数每公里改正数各测段的改正数每一站改正数各测段的改正数计算的基本步骤高差闭合差的计算闭合差的调整高程的计算(见例题2)例题2高程误差配赋表首先：将检查无误的野外观测成果填入计算表，包括：各测段的距离和高差值h i已知数据第一步：高差闭合差的计算第二步：高差闭合差的调整各测段实测高差加改正数，得改正后的高差h i第三步：待定点高程的计算根据改正后的高差h i，由起始点Ⅲ18开始，逐点推算出各点的高程，列入表中最后算得的Ⅲ19点的高程应与已知的高程HⅢ19相等，否则说明闭合水准路线闭合水准路线的成果计算与附合水准路线基本相同，不同之处是检核条件与附合水准路线不同。