高考数学专题训练19特例检验型逆向思维型综合型理

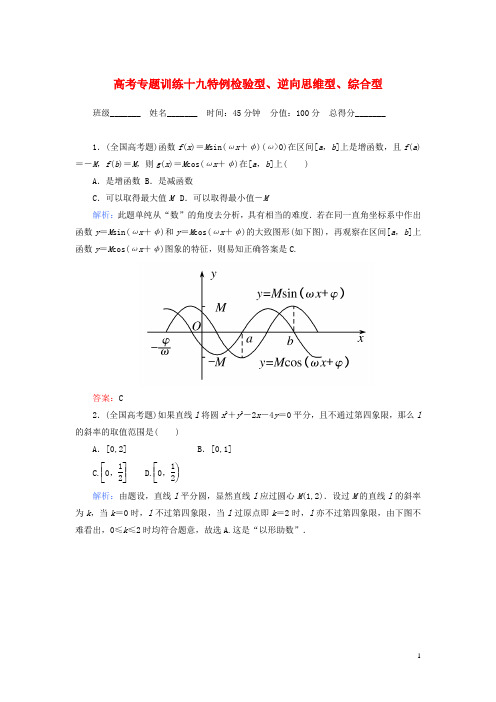
高考专题训练十九特例检验型、逆向思维型、综合型班级_______ 姓名_______ 时间：45分钟 分值：100分 总得分_______1．(全国高考题)函数f (x )＝M sin(ωx ＋φ)(ω>0)在区间[a ，b ]上是增函数，且f (a )＝－M ，f (b )＝M ，则g (x )＝M cos(ωx ＋φ)在[a ，b ]上( )A ．是增函数B ．是减函数C ．可以取得最大值MD ．可以取得最小值－M解析：此题单纯从“数”的角度去分析，具有相当的难度．若在同一直角坐标系中作出函数y ＝M sin(ωx ＋φ)和y ＝M cos(ωx ＋φ)的大致图形(如下图)，再观察在区间[a ，b ]上函数y ＝M cos(ωx ＋φ)图象的特征，则易知正确答案是C.答案：C2．(全国高考题)如果直线l 将圆x 2＋y 2－2x －4y ＝0平分，且不通过第四象限，那么l 的斜率的取值范围是( )A ．[0,2]B ．[0,1] C.⎣⎡⎦⎤0，12 D.⎣⎡⎭⎫0，12 解析：由题设，直线l 平分圆，显然直线l 应过圆心M (1,2)．设过M 的直线l 的斜率为k ，当k ＝0时，l 不过第四象限，当l 过原点即k ＝2时，l 亦不过第四象限，由下图不难看出，0≤k ≤2时均符合题意，故选A.这是“以形助数”．答案：A3．(全国高考题)定义在(－∞，＋∞)上的奇函数f(x)为增函数，偶函数g(x)在区间[0，＋∞)的图象与f(x)的图象重合．设a>b>0，给出下列不等式：①f(b)－f(－a)>g(a)－g(－b)，②f(b)－f(－a)<g(a)－g(－b)，③f(a)－f(－b)>g(b)－g(－a)，④f(a)－f(－b)<g(b)－g(－a)．其中成立的是( )A．①②B．②③C．①③D．②④解析：依题意画出f(x)在[0，＋∞)上的示意图(如下图)从图中易得：由f(x)奇，g(x)偶有，f(a)＝g(a)＝g(－a)＝－f(－a)，f(b)＝g(b)＝g(－b)＝－f(－b)，f(b)－f(－a)＝f(b)＋f(a)＝g(b)＋g(a)>g(a)－g(－b)，f(a)－f(－b)＝f(a)＋f(b)＝g(a)＋g(b)>g(b)－g(－a)．故选C. 答案：C4．如果函数y ＝sin2x ＋a cos2x 的图象关于直线x ＝－π8对称，则实数a 的值为( )A. 2 B ．－ 2 C ．1 D ．－1分析：函数f (x )在x ＝－π8时取得最值；或考虑有f ⎝⎛⎭⎫－π8＋x ＝f ⎝⎛⎭⎫－π8－x 对一切x ∈R 恒成立．解析：解法一：设f (x )＝sin2x ＋a cos2x ，因为函数的图象关于直线x ＝－π8对称，所以f ⎝⎛⎭⎫－π8＋x ＝f ⎝⎛⎭⎫－π8－x 对一切实数x 都成立， 即sin2⎝⎛⎭⎫－π8＋x ＋a cos2⎝⎛⎭⎫－π8＋x ＝sin2⎝⎛⎭⎫－π8－x ＋a cos2⎝⎛⎭⎫－π8－x 即sin ⎝⎛⎭⎫－π4＋2x ＋sin ⎝⎛⎭⎫π4＋2x ＝a ⎣⎡⎦⎤cos ⎝⎛⎭⎫π4＋2x －cos ⎝⎛⎭⎫－π4＋2x ， ∴2sin2x ²cosπ4＝－2a sin2x ²sin π4， 即(a ＋1)²sin2x ＝0对一切实数x 恒成立，而sin2x 不能恒为0， ∴a ＋1＝0，即a ＝－1，故选D.解法二：∵f (x )＝sin2x ＋a cos2x 关于直线x ＝－π8∴有f ⎝⎛⎭⎫－π8＋x ＝f ⎝⎛⎭⎫－π8－x 对一切x ∈R 恒成立． 特别，对于x ＝π8将x ＝π8代入上式，得f (0)＝f ⎝⎛⎭⎫－π4， ∴sin0＋a cos0＝sin ⎝⎛⎭⎫－π2＋a cos ⎝⎛⎭⎫－π2 ∴0＋a ＝－1＋a ³0. ∴a ＝－1.故选D.解法三：y ＝sin2x ＋a cos2x ＝1＋a 2sin(2x ＋φ)，其中角φ的终边经过点(1，a )．其图象的对称轴方程为2x ＋φ＝k π＋π2(k ∈Z)， 即x ＝k π2＋π4－φ2(k ∈Z)． 令k π2＋π4－φ2＝－π8k ∈Z)． 得φ＝k π＋3π4(k ∈Z)． 但角φ的终边经过点(1，a )，故k 为奇数，角φ的终边与－π2角的终边相同，∴a ＝－1.故选D.解法四：y ＝sin2x ＋a cos2x ＝1＋a 2sin(2x ＋φ)，其中角φ满足tan φ＝a .因为f (x )的对称轴为y ＝－π8， ∴当x ＝－π8时函数y ＝f (x )有最大值或最小值，所以1＋a 2＝f ⎝⎛⎭⎫－π8或－1＋a 2＝f ⎝⎛⎭⎫－π8， 即1＋a 2＝sin ⎝⎛⎫－π4＋a cos ⎝⎛⎫－π4， 或－1＋a 2＝sin ⎝⎛⎭⎫－π4＋a cos ⎝⎛⎭⎫－π4. 解之得a ＝－1.故选D. 答案：D评析：本题给出了四种不同的解法，充分利用函数图象的对称性的特征来解题．解法一是运用了方程思想或恒等式思想求解．解法二是利用了数形结合的思想求解，抓住f (m ＋x )＝f (m －x )的图象关于直线x ＝m 对称的性质，取特殊值来求出待定系数a 的值．解法三利用函数y ＝A sin(ωx ＋φ)的对称轴是方程ωx ＋φ＝k π＋π2(k ∈Z)的解x ＝k π＋π2－φω(k ∈Z)，然后将x ＝－π8代入求出相应的φ值，再求a 的值．解法四利用对称轴的特殊性质，在此处函数f (x )取最大值或最小值．于是有f ⎝⎛⎭⎫－π8＝[f (x )]max 或f ⎝⎛⎭⎫－π8＝[f (x )]min.从而转化为解方程问题，体现了方程思想．由此可见，本题体现了丰富的数学思想方法，要从多种解法中悟出其实质东西．5．△ABC 的外接圆的圆心为O ，两条边上的高的交点为H ，OH →＝m (OA →＋OB →＋OC →)，则实数m 的值为( )A.12B ．1C ．2 D.22解析：当△ABC 为等腰直角三角形时，O 为AC 的中点，AB 、BC 边上高的交点H 与B 重合(如图)，OA →＋OB →＋OC →＝OB →＝OH →，所以m ＝1.答案：B6．设f (x )是定义在实数集R 上的任意一个增函数，且F (x )＝f (x )－f (－x )，那么F (x )应为( )A ．增函数且是奇函数B ．增函数且为偶函数C ．减函数且是奇函数D ．减函数且为偶函数解析：因为f (x )是定义在R 上的任意一个增函数，可取f (x )＝x ，知F (x )＝x －(－x )＝2x ，故选A.答案：A7．若sin α＋sin β＝13(cos β－cos α)，α、β∈(0，π)．则α－β的值为( )A ．－2π3B ．－π3C.π3 D.2π3解析：由sin α＋sin β＝13(cos β－cos α)及α、β的范围，可直接推α－β的值，但运算量较大．令β＝π6代入，得sin α＝－13cos α，即tan α＝－33，α∈(0，π)，∴α＝5π6.∴α－β＝5π6－π6＝2π3，故选D. 答案：D8．(全国高考题)若a >b >1，P ＝lg a ² lg b ，Q ＝12(lg a ＋lg b )，R ＝lg ⎝⎛⎭⎫a ＋b 2，则( )A ．R <P <QB ．P <Q <RC ．Q <P <RD ．P <R <Q解析：取a ＝100，b ＝10，则P ＝2，Q ＝1.5，R ＝lg 1102>lg 1002＝2－lg2>Q ，故应选B.答案：B 9．若0<|α|<π4，则( ) A ．sin2α>sin α B ．cos2α<cos α C ．tan2α>tan α D ．cot2α>cot α解析：取α＝±π6，可否定A 、C 、D ，因此选B. 答案：B10．命题甲：x ≠2或y ≠3；命题乙：x ＋y ≠5，则( ) A ．甲是乙的充分不必要条件 B ．甲是乙的必要不充分条件 C ．甲是乙的充要条件D ．甲既不是乙的充分条件，也不是乙的必要条件解析：“甲⇒乙”，即“x ≠2或y ≠3⇒x ＋y ≠5”，其逆否命题为：“x ＋y ＝5”⇒“x ＝2且y ＝3”显然不正确．同理，可判断命题“乙⇒甲”为真命题．所以选B.答案：B11．定义：离心率e ＝5－12的椭圆为“黄金椭圆”．对于椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)，如果a ，b ，c 不是等比数列，那么椭圆E ( )A ．一定是“黄金椭圆”B ．一定不是“黄金椭圆”C ．可能是“黄金椭圆”D ．可能不是“黄金椭圆”解析：假设E 为黄金椭圆，则有e ＝c a ＝5－12，即c ＝5－12a .所以b 2＝a 2－c 2＝a 2－⎝⎛⎭⎪⎫5－12a 2＝5－12a 2＝ac ， 这说明a ，b ，c 成等比数列，与已知矛盾，故椭圆E 一定不是“黄金椭圆”．故选B. 答案：B12．若焦点在x 轴上的椭圆x 22＋y 2m ＝1的离心率为12，则m ＝( )A. 3B.32C.83D.23解析：假设m ＝32，则c 2＝2－32＝12，c ＝22e ＝c a ＝12故选B.答案：B13．若圆x 2＋y 2＝r 2上恰有相异两点到直线4x －3y ＋25＝0的距离等于1，则r 的取值范围是( )A ．[4,6]B ．[4,6)C ．(4,6]D ．(4,6)解析：因为圆心O (0,0)到直线4x －3y ＋25＝0的距离d ＝5，若r ＝4，则圆上只有一点到直线的距离等于1，故r ≠4.又若r ＝6，则圆上有三点到直线的距离等于1，故r ≠6.所以选D.答案：D14．对任意的锐角α、β，下列不等关系中正确的是( ) A ．sin(α＋β)>sin α＋sin β B ．sin(α＋β)>cos α＋cos β C ．cos(α＋β)<sin α＋sin β D ．cos(α＋β)<cos α＋cos β解析：当α＝β＝30°时，可排除A 、B 选项，当α＝β＝15°时，代入C 选项中，即0<cos30°<2sin15°，两边平方，34＝0.75<4sin 215°＝4³1－cos30°2＝2－3≈0.268矛盾．故选D.答案：D15．在△ABC 中，有命题：①AB →－AC →＝BC →；②AB →＋BC →＋CA →＝0；③若(AB →＋AC →)²(AB →－AC →)＝0，则△ABC 为等腰三角形；④若AC →²AB →>0，则△ABC 为锐角三角形．上述命题正确的是( )A ．①②B ．①④C ．②③D ．②③④ 解析：∵AB →－AC →＝CB →易知①错，②、③都正确．而AC →²AB →>0⇒|AC →||AB →|cos A >0⇒∠A 为锐角，不能断言△ABC 为锐角三角形，即④错．答案：C16．已知函数f (x )＝ax 2＋bx ＋c (a ，b ，c ∈R ，a <0)对于一切实数x ，f (1－x )＝f (1＋x )均成立，且f (－1)<0，f (0)>0.则有( )A ．a ＋b ＋c <0B ．b <a ＋cC ．c <2bD ．abc >0解析：(排除法)由题设可知抛物线的对称轴为x ＝1，即 －b2a＝1，b ＝－2a >0.f (－1)＝a －b ＋c <0⇒a ＋c <b ，排除 B.f (1)＝a ＋b ＋c >0，排除A.a <0，f (0)＝c >0，b >0，排除D.另外选项C 的正确性可如下证明：a ＋c <b ⇒c <b －a <b －2a ＝2b .答案：C17．对于函数①f (x )＝|x ＋2|；②f (x )＝(x －2)2；③f (x )＝cos(x －2)． 判断如下两个命题的真假： 命题甲：f (x ＋2)是偶函数；命题乙：f (x )在(－∞，2)上是减函数，在(2，＋∞)上是增函数； 能使命题甲、乙均为真的所有函数的序号是( ) A ．①②B ．①③C ．②D ．③解析：命题甲f (x ＋2)是偶函数，可知②③满足条件，排除①；作出②③函数的图象，可知③不满足命题乙的条件，所以选C.答案：C18．已知四边形ABCD 为菱形，点P 在对角线AC 上(不包括端点A 、C )，则AP →等于( )A ．λ(AB →＋AD →)，λ∈(0,1)B ．λ(AB →＋BC →)，λ∈⎝ ⎛⎭⎪⎫0，22 C ．λ(AB →－AD →)，λ∈(0,1) D ．λ(AB →－BC →)，λ∈⎝ ⎛⎭⎪⎫0，22 解析：λ(AB →＋AD →)＝λAC →，当λ∈(0,1)时，|λAC →|＝λ|AC →|∈(0，|AC →|)，而选项B 中λ(AB →＋BC →)∈⎝ ⎛⎭⎪⎫0，22|AC →|，不满足条件，选项C 、D则显然不正确，故选A.答案：A19．(2011²陕西模拟)如图所示，O ，A ，B 是平面上三点，向量OA →＝a ，OB →＝b .在平面AOB 上，P 是线段AB 垂直平分线上任意一点，向量OP →＝p ，且|a |＝3，|b |＝2，则p ²(a －b )的值是( )A ．5 B.52C ．3 D.32解析：因为P 是线段AB 垂直平分线上任意一点，不妨设P 为AB 的中点，则有OP →＝p ＝12(a ＋b )．∴p ²(a －b )＝12(|a |2－|b |2)．∵|a |＝3，|b |＝2， ∴p ²(a －b )＝52.答案：B20．在△ABC 中，已知D 是AB 边上一点，若AD →＝2DB →，CD →＝13CA →＋λCB →，则λ等于( )A.23B.13C ．－13D ．－23解析：取△ABC 为等腰三角形，如图所示，则有CD →＝CE →＋CF →，此时CE →＝13→，CF →＝23CB →，而CD →＝13CA →＋λCB →，故λ＝23. 答案：A。

马井堂-数学-高考专题训练十九特例检验型、逆向思维型、综合型班级_______ 姓名_______ 时间：45分钟 分值：100分 总得分_______1．(全国高考题)函数f (x )＝M sin(ωx ＋φ)(ω>0)在区间[a ，b ]上是增函数，且f (a )＝－M ，f (b )＝M ，则g (x )＝M cos(ωx ＋φ)在[a ，b ]上( )A ．是增函数B ．是减函数C ．可以取得最大值MD ．可以取得最小值－M解析：此题单纯从“数”的角度去分析，具有相当的难度．若在同一直角坐标系中作出函数y ＝M sin(ωx ＋φ)和y ＝M cos(ωx ＋φ)的大致图形(如下图)，再观察在区间[a ，b ]上函数y ＝M cos(ωx ＋φ)图象的特征，则易知正确答案是C.答案：C2．(全国高考题)如果直线l 将圆x 2＋y 2－2x －4y ＝0平分，且不通过第四象限，那么l 的斜率的取值范围是( )A ．[0,2]B ．[0,1]C.⎣⎢⎡⎦⎥⎤0，12 D.⎣⎢⎡⎭⎪⎫0，12 解析：由题设，直线l 平分圆，显然直线l 应过圆心M (1,2)．设过M的直线l的斜率为k，当k＝0时，l不过第四象限，当l过原点即k＝2时，l亦不过第四象限，由下图不难看出，0≤k≤2时均符合题意，故选A.这是“以形助数”．答案：A3．(全国高考题)定义在(－∞，＋∞)上的奇函数f(x)为增函数，偶函数g(x)在区间[0，＋∞)的图象与f(x)的图象重合．设a>b>0，给出下列不等式：①f(b)－f(－a)>g(a)－g(－b)，②f(b)－f(－a)<g(a)－g(－b)，③f(a)－f(－b)>g(b)－g(－a)，④f(a)－f(－b)<g(b)－g(－a)．其中成立的是()A．①②B．②③C．①③D．②④解析：依题意画出f(x)在[0，＋∞)上的示意图(如下图)从图中易得：由f (x )奇，g (x )偶有， f (a )＝g (a )＝g (－a )＝－f (－a )， f (b )＝g (b )＝g (－b )＝－f (－b )，f (b )－f (－a )＝f (b )＋f (a )＝g (b )＋g (a )>g (a )－g (－b )， f (a )－f (－b )＝f (a )＋f (b )＝g (a )＋g (b )>g (b )－g (－a )． 故选C. 答案：C4．如果函数y ＝sin2x ＋a cos2x 的图象关于直线x ＝－π8对称，则实数a 的值为( )A. 2 B ．－ 2 C ．1D ．－1分析：函数f (x )在x ＝－π8时取得最值；或考虑有f ⎝⎛⎭⎪⎫－π8＋x ＝f ⎝⎛⎭⎪⎫－π8－x 对一切x ∈R 恒成立． 解析：解法一：设f (x )＝sin2x ＋a cos2x ，因为函数的图象关于直线x ＝－π8对称，所以f ⎝ ⎛⎭⎪⎫－π8＋x ＝f ⎝ ⎛⎭⎪⎫－π8－x 对一切实数x 都成立，即sin2⎝ ⎛⎭⎪⎫－π8＋x ＋a cos2⎝ ⎛⎭⎪⎫－π8＋x ＝sin2⎝ ⎛⎭⎪⎫－π8－x ＋a cos2⎝ ⎛⎭⎪⎫－π8－x 即sin ⎝ ⎛⎭⎪⎫－π4＋2x ＋sin ⎝ ⎛⎭⎪⎫π4＋2x ＝a ⎣⎢⎡⎦⎥⎤cos ⎝⎛⎭⎪⎫π4＋2x －cos ⎝⎛⎭⎪⎫－π4＋2x ， ∴2sin2x ·cos π4＝－2a sin2x ·sin π4，即(a ＋1)·sin2x ＝0对一切实数x 恒成立，而sin2x 不能恒为0， ∴a ＋1＝0，即a ＝－1，故选D.解法二：∵f (x )＝sin2x ＋a cos2x 关于直线x ＝－π8对称．∴有f ⎝⎛⎭⎪⎫－π8＋x ＝f ⎝⎛⎭⎪⎫－π8－x 对一切x ∈R 恒成立．特别，对于x ＝π8应该成立．将x ＝π8代入上式，得f (0)＝f ⎝ ⎛⎭⎪⎫－π4，∴sin0＋a cos0＝sin ⎝⎛⎭⎪⎫－π2＋a cos ⎝⎛⎭⎪⎫－π2∴0＋a ＝－1＋a ×0. ∴a ＝－1.故选D.解法三：y ＝sin2x ＋a cos2x ＝1＋a 2sin(2x ＋φ)，其中角φ的终边经过点(1，a )．其图象的对称轴方程为2x ＋φ＝k π＋π2(k ∈Z)，即x ＝k π2＋π4－φ2(k ∈Z)．令k π2＋π4－φ2＝－π8(k ∈Z)．得φ＝k π＋3π4(k ∈Z)．但角φ的终边经过点(1，a )，故k 为奇数，角φ的终边与－π2角的终边相同，∴a ＝－1.故选D.解法四：y ＝sin2x ＋a cos2x ＝1＋a 2sin(2x ＋φ)，其中角φ满足tan φ＝a .因为f (x )的对称轴为y ＝－π8，∴当x ＝－π8时函数y ＝f (x )有最大值或最小值，所以1＋a 2＝f ⎝⎛⎭⎪⎫－π8或－1＋a 2＝f ⎝⎛⎭⎪⎫－π8，即1＋a 2＝sin ⎝⎛⎭⎪⎫－π4＋a cos ⎝⎛⎭⎪⎫－π4，或－1＋a 2＝sin ⎝ ⎛⎭⎪⎫－π4＋a cos ⎝ ⎛⎭⎪⎫－π4.解之得a ＝－1.故选D. 答案：D评析：本题给出了四种不同的解法，充分利用函数图象的对称性的特征来解题．解法一是运用了方程思想或恒等式思想求解．解法二是利用了数形结合的思想求解，抓住f (m ＋x )＝f (m －x )的图象关于直线x ＝m 对称的性质，取特殊值来求出待定系数a 的值．解法三利用函数y ＝A sin(ωx ＋φ)的对称轴是方程ωx ＋φ＝k π＋π2(k ∈Z)的解x ＝k π＋π2－φω(k ∈Z)，然后将x ＝－π8代入求出相应的φ值，再求a 的值．解法四利用对称轴的特殊性质，在此处函数f (x )取最大值或最小值．于是有f ⎝ ⎛⎭⎪⎫－π8＝[f (x )]max 或f ⎝ ⎛⎭⎪⎫－π8＝[f (x )]min .从而转化为解方程问题，体现了方程思想．由此可见，本题体现了丰富的数学思想方法，要从多种解法中悟出其实质东西．5．△ABC 的外接圆的圆心为O ，两条边上的高的交点为H ，OH →＝m (OA →＋OB →＋OC →)，则实数m 的值为( )A.12 B ．1 C ．2 D.22解析：当△ABC 为等腰直角三角形时，O 为AC 的中点，AB 、BC 边上高的交点H 与B 重合(如图)，OA →＋OB →＋OC →＝OB →＝OH →，所以m ＝1.答案：B6．设f (x )是定义在实数集R 上的任意一个增函数，且F (x )＝f (x )－f (－x )，那么F (x )应为( )A ．增函数且是奇函数B ．增函数且为偶函数C ．减函数且是奇函数D ．减函数且为偶函数解析：因为f (x )是定义在R 上的任意一个增函数，可取f (x )＝x ，知F (x )＝x －(－x )＝2x ，故选A.答案：A7．若sin α＋sin β＝13(cos β－cos α)，α、β∈(0，π)．则α－β的值为( )A ．－2π3B ．－π3C.π3D.2π3解析：由sin α＋sin β＝13(cos β－cos α)及α、β的范围，可直接推α－β的值，但运算量较大．令β＝π6代入，得sin α＝－13cos α，即tan α＝－33，α∈(0，π)，∴α＝5π6.∴α－β＝5π6－π6＝2π3，故选D.答案：D8．(全国高考题)若a >b >1，P ＝lg a · lg b ，Q ＝12(lg a ＋lg b )，R ＝lg ⎝⎛⎭⎪⎫a ＋b 2，则( ) A ．R <P <Q B ．P <Q <R C ．Q <P <RD ．P <R <Q解析：取a ＝100，b ＝10，则P ＝2，Q ＝1.5，R ＝lg 1102>lg 1002＝2－lg2>Q ，故应选B.答案：B9．若0<|α|<π4，则( )A ．sin2α>sin αB ．cos2α<cos αC ．tan2α>tan αD ．cot2α>cot α解析：取α＝±π6，可否定A 、C 、D ，因此选B.答案：B10．命题甲：x ≠2或y ≠3；命题乙：x ＋y ≠5，则( ) A ．甲是乙的充分不必要条件 B ．甲是乙的必要不充分条件 C ．甲是乙的充要条件D ．甲既不是乙的充分条件，也不是乙的必要条件解析：“甲⇒乙”，即“x ≠2或y ≠3⇒x ＋y ≠5”，其逆否命题为：“x ＋y ＝5”⇒“x ＝2且y ＝3”显然不正确．同理，可判断命题“乙⇒甲”为真命题．所以选B.答案：B11．定义：离心率e ＝5－12的椭圆为“黄金椭圆”．对于椭圆E ：x 2a 2＋y 2b2＝1(a >b >0)，如果a ，b ，c 不是等比数列，那么椭圆E ( ) A ．一定是“黄金椭圆” B ．一定不是“黄金椭圆” C ．可能是“黄金椭圆” D ．可能不是“黄金椭圆” 解析：假设E 为黄金椭圆，则有 e ＝ca ＝5－12，即c ＝5－12a .所以b 2＝a 2－c 2＝a 2－⎝ ⎛⎭⎪⎫5－12a 2＝5－12a 2＝ac ，这说明a ，b ，c 成等比数列，与已知矛盾，故椭圆E 一定不是“黄金椭圆”．故选B.答案：B12．若焦点在x 轴上的椭圆x 22＋y 2m ＝1的离心率为12，则m ＝( )A. 3B.32C.83D.23解析：假设m ＝32，则c 2＝2－32＝12，c ＝22，e ＝c a ＝12.故选B.答案：B13．若圆x 2＋y 2＝r 2上恰有相异两点到直线4x －3y ＋25＝0的距离等于1，则r 的取值范围是( )A ．[4,6]B ．[4,6)C ．(4,6]D ．(4,6)解析：因为圆心O (0,0)到直线4x －3y ＋25＝0的距离d ＝5，若r ＝4，则圆上只有一点到直线的距离等于1，故r ≠4.又若r ＝6，则圆上有三点到直线的距离等于1，故r ≠6.所以选D.答案：D14．对任意的锐角α、β，下列不等关系中正确的是( ) A ．sin(α＋β)>sin α＋sin β B ．sin(α＋β)>cos α＋cos β C ．cos(α＋β)<sin α＋sin β D ．cos(α＋β)<cos α＋cos β解析：当α＝β＝30°时，可排除A 、B 选项，当α＝β＝15°时，代入C 选项中，即0<cos30°<2sin15°，两边平方，34＝0.75<4sin 215°＝4×1－cos30°2＝2－3≈0.268矛盾．故选D.答案：D15．在△ABC 中，有命题：①AB →－AC →＝BC →；②AB →＋BC →＋CA →＝0；③若(AB →＋AC →)·(AB →－AC →)＝0，则△ABC 为等腰三角形；④若AC →·AB →>0，则△ABC 为锐角三角形．上述命题正确的是( )A ．①②B ．①④C ．②③D ．②③④解析：∵AB →－AC →＝CB →易知①错，②、③都正确．而AC →·AB →>0⇒|AC →||AB →|cos A >0⇒∠A 为锐角，不能断言△ABC 为锐角三角形，即④错．答案：C16．已知函数f (x )＝ax 2＋bx ＋c (a ，b ，c ∈R ，a <0)对于一切实数x ，f (1－x )＝f (1＋x )均成立，且f (－1)<0，f (0)>0.则有( )A ．a ＋b ＋c <0B ．b <a ＋cC ．c <2bD ．abc >0解析：(排除法)由题设可知抛物线的对称轴为x ＝1，即 －b2a ＝1，b ＝－2a >0.f (－1)＝a －b ＋c <0⇒a ＋c <b ，排除 B.f (1)＝a ＋b ＋c >0，排除A.a <0，f (0)＝c >0，b >0，排除D.另外选项C 的正确性可如下证明： a ＋c <b ⇒c <b －a <b －2a ＝2b . 答案：C17．对于函数①f (x )＝|x ＋2|；②f (x )＝(x －2)2；③f (x )＝cos(x －2)． 判断如下两个命题的真假：命题甲：f (x ＋2)是偶函数；命题乙：f (x )在(－∞，2)上是减函数，在(2，＋∞)上是增函数； 能使命题甲、乙均为真的所有函数的序号是( )A ．①②B ．①③C ．②D ．③解析：命题甲f (x ＋2)是偶函数，可知②③满足条件，排除①；作出②③函数的图象，可知③不满足命题乙的条件，所以选C.答案：C18．已知四边形ABCD 为菱形，点P 在对角线AC 上(不包括端点A 、C )，则AP →等于( )A ．λ(AB →＋AD →)，λ∈(0,1)B ．λ(AB →＋BC →)，λ∈⎝⎛⎭⎪⎫0，22 C ．λ(AB →－AD →)，λ∈(0,1)D ．λ(AB →－BC →)，λ∈⎝⎛⎭⎪⎫0，22 解析：λ(AB →＋AD →)＝λAC →，当λ∈(0,1)时，|λAC →|＝λ|AC →|∈(0，|AC →|)，而选项B 中λ(AB →＋BC →)∈⎝ ⎛⎭⎪⎪⎫0，22|AC →|，不满足条件，选项C 、D 则显然不正确，故选A.答案：A19．(2011·陕西模拟)如图所示，O ，A ，B 是平面上三点，向量OA →＝a ，OB →＝b .在平面AOB 上，P 是线段AB 垂直平分线上任意一点，向量OP →＝p ，且|a |＝3，|b |＝2，则p ·(a －b )的值是( )A ．5B.52 C ．3 D.32解析：因为P 是线段AB 垂直平分线上任意一点，不妨设P 为AB 的中点，则有OP →＝p ＝12(a ＋b )． ∴p ·(a －b )＝12(|a |2－|b |2)． ∵|a |＝3，|b |＝2，∴p ·(a －b )＝52. 答案：B20．在△ABC 中，已知D 是AB 边上一点，若AD →＝2DB →，CD →＝13CA →＋λCB →，则λ等于( ) A.23B.13 C ．－13D ．－23解析：取△ABC 为等腰三角形，如图所示，则有CD →＝CE →＋CF →，此时CE→＝13CA →，CF →＝23CB →，而CD →＝13CA →＋λCB →，故λ＝23. 答案：A。

高考专题训练十九特例检验型、逆向思维型、综合型班级_______ 姓名_______ 时间：45分钟 分值：100分 总得分_______1．(全国高考题)函数f (x )＝M sin(ωx ＋φ)(ω>0)在区间[a ，b ]上是增函数，且f (a )＝－M ，f (b )＝M ，则g (x )＝M cos(ωx ＋φ)在[a ，b ]上( )A ．是增函数B ．是减函数C ．可以取得最大值MD ．可以取得最小值－M解析：此题单纯从“数”的角度去分析，具有相当的难度．若在同一直角坐标系中作出函数y ＝M sin(ωx ＋φ)和y ＝M cos(ωx ＋φ)的大致图形(如下图)，再观察在区间[a ，b ]上函数y ＝M cos(ωx ＋φ)图象的特征，则易知正确答案是C.答案：C2．(全国高考题)如果直线l 将圆x 2＋y 2－2x －4y ＝0平分，且不通过第四象限，那么l 的斜率的取值范围是( )A ．[0,2]B ．[0,1]C.⎣⎢⎡⎦⎥⎤0，12 D.⎣⎢⎡⎭⎪⎫0，12 解析：由题设，直线l 平分圆，显然直线l 应过圆心M (1,2)．设过M的直线l的斜率为k，当k＝0时，l不过第四象限，当l过原点即k＝2时，l亦不过第四象限，由下图不难看出，0≤k≤2时均符合题意，故选A.这是“以形助数”．答案：A3．(全国高考题)定义在(－∞，＋∞)上的奇函数f(x)为增函数，偶函数g(x)在区间[0，＋∞)的图象与f(x)的图象重合．设a>b>0，给出下列不等式：①f(b)－f(－a)>g(a)－g(－b)，②f(b)－f(－a)<g(a)－g(－b)，③f(a)－f(－b)>g(b)－g(－a)，④f(a)－f(－b)<g(b)－g(－a)．其中成立的是()A．①②B．②③C．①③D．②④解析：依题意画出f(x)在[0，＋∞)上的示意图(如下图)从图中易得：由f (x )奇，g (x )偶有， f (a )＝g (a )＝g (－a )＝－f (－a )， f (b )＝g (b )＝g (－b )＝－f (－b )，f (b )－f (－a )＝f (b )＋f (a )＝g (b )＋g (a )>g (a )－g (－b )， f (a )－f (－b )＝f (a )＋f (b )＝g (a )＋g (b )>g (b )－g (－a )． 故选C. 答案：C4．如果函数y ＝sin2x ＋a cos2x 的图象关于直线x ＝－π8对称，则实数a 的值为( )A. 2 B ．－ 2 C ．1D ．－1分析：函数f (x )在x ＝－π8时取得最值；或考虑有f ⎝⎛⎭⎪⎫－π8＋x ＝f ⎝⎛⎭⎪⎫－π8－x 对一切x ∈R 恒成立． 解析：解法一：设f (x )＝sin2x ＋a cos2x ，因为函数的图象关于直线x ＝－π8对称，所以f ⎝ ⎛⎭⎪⎫－π8＋x ＝f ⎝ ⎛⎭⎪⎫－π8－x 对一切实数x 都成立，即sin2⎝ ⎛⎭⎪⎫－π8＋x ＋a cos2⎝ ⎛⎭⎪⎫－π8＋x ＝sin2⎝ ⎛⎭⎪⎫－π8－x ＋a cos2⎝ ⎛⎭⎪⎫－π8－x 即sin ⎝ ⎛⎭⎪⎫－π4＋2x ＋sin ⎝ ⎛⎭⎪⎫π4＋2x ＝a ⎣⎢⎡⎦⎥⎤cos ⎝⎛⎭⎪⎫π4＋2x －cos ⎝⎛⎭⎪⎫－π4＋2x ， ∴2sin2x ·cos π4＝－2a sin2x ·sin π4，即(a ＋1)·sin2x ＝0对一切实数x 恒成立，而sin2x 不能恒为0， ∴a ＋1＝0，即a ＝－1，故选D.解法二：∵f (x )＝sin2x ＋a cos2x 关于直线x ＝－π8对称．∴有f ⎝⎛⎭⎪⎫－π8＋x ＝f ⎝⎛⎭⎪⎫－π8－x 对一切x ∈R 恒成立．特别，对于x ＝π8应该成立．将x ＝π8代入上式，得f (0)＝f ⎝ ⎛⎭⎪⎫－π4，∴sin0＋a cos0＝sin ⎝⎛⎭⎪⎫－π2＋a cos ⎝⎛⎭⎪⎫－π2∴0＋a ＝－1＋a ×0. ∴a ＝－1.故选D.解法三：y ＝sin2x ＋a cos2x ＝1＋a 2sin(2x ＋φ)，其中角φ的终边经过点(1，a )．其图象的对称轴方程为2x ＋φ＝k π＋π2(k ∈Z)，即x ＝k π2＋π4－φ2(k ∈Z)．令k π2＋π4－φ2＝－π8(k ∈Z)．得φ＝k π＋3π4(k ∈Z)．但角φ的终边经过点(1，a )，故k 为奇数，角φ的终边与－π2角的终边相同，∴a ＝－1.故选D.解法四：y ＝sin2x ＋a cos2x ＝1＋a 2sin(2x ＋φ)，其中角φ满足tan φ＝a .因为f (x )的对称轴为y ＝－π8，∴当x ＝－π8时函数y ＝f (x )有最大值或最小值，所以1＋a 2＝f ⎝⎛⎭⎪⎫－π8或－1＋a 2＝f ⎝⎛⎭⎪⎫－π8，即1＋a 2＝sin ⎝⎛⎭⎪⎫－π4＋a cos ⎝⎛⎭⎪⎫－π4，或－1＋a 2＝sin ⎝ ⎛⎭⎪⎫－π4＋a cos ⎝ ⎛⎭⎪⎫－π4.解之得a ＝－1.故选D. 答案：D评析：本题给出了四种不同的解法，充分利用函数图象的对称性的特征来解题．解法一是运用了方程思想或恒等式思想求解．解法二是利用了数形结合的思想求解，抓住f (m ＋x )＝f (m －x )的图象关于直线x ＝m 对称的性质，取特殊值来求出待定系数a 的值．解法三利用函数y ＝A sin(ωx ＋φ)的对称轴是方程ωx ＋φ＝k π＋π2(k ∈Z)的解x ＝k π＋π2－φω(k ∈Z)，然后将x ＝－π8代入求出相应的φ值，再求a 的值．解法四利用对称轴的特殊性质，在此处函数f (x )取最大值或最小值．于是有f ⎝ ⎛⎭⎪⎫－π8＝[f (x )]max 或f ⎝ ⎛⎭⎪⎫－π8＝[f (x )]min .从而转化为解方程问题，体现了方程思想．由此可见，本题体现了丰富的数学思想方法，要从多种解法中悟出其实质东西．5．△ABC 的外接圆的圆心为O ，两条边上的高的交点为H ，OH →＝m (OA →＋OB →＋OC →)，则实数m 的值为( )A.12 B ．1 C ．2 D.22解析：当△ABC 为等腰直角三角形时，O 为AC 的中点，AB 、BC 边上高的交点H 与B 重合(如图)，OA →＋OB →＋OC →＝OB →＝OH →，所以m ＝1.答案：B6．设f (x )是定义在实数集R 上的任意一个增函数，且F (x )＝f (x )－f (－x )，那么F (x )应为( )A ．增函数且是奇函数B ．增函数且为偶函数C ．减函数且是奇函数D ．减函数且为偶函数解析：因为f (x )是定义在R 上的任意一个增函数，可取f (x )＝x ，知F (x )＝x －(－x )＝2x ，故选A.答案：A7．若sin α＋sin β＝13(cos β－cos α)，α、β∈(0，π)．则α－β的值为( )A ．－2π3B ．－π3C.π3D.2π3解析：由sin α＋sin β＝13(cos β－cos α)及α、β的范围，可直接推α－β的值，但运算量较大．令β＝π6代入，得sin α＝－13cos α，即tan α＝－33，α∈(0，π)，∴α＝5π6.∴α－β＝5π6－π6＝2π3，故选D.答案：D8．(全国高考题)若a >b >1，P ＝lg a · lg b ，Q ＝12(lg a ＋lg b )，R ＝lg ⎝⎛⎭⎪⎫a ＋b 2，则( ) A ．R <P <Q B ．P <Q <R C ．Q <P <RD ．P <R <Q解析：取a ＝100，b ＝10，则P ＝2，Q ＝1.5，R ＝lg 1102>lg 1002＝2－lg2>Q ，故应选B.答案：B9．若0<|α|<π4，则( )A ．sin2α>sin αB ．cos2α<cos αC ．tan2α>tan αD ．cot2α>cot α解析：取α＝±π6，可否定A 、C 、D ，因此选B.答案：B10．命题甲：x ≠2或y ≠3；命题乙：x ＋y ≠5，则( ) A ．甲是乙的充分不必要条件 B ．甲是乙的必要不充分条件 C ．甲是乙的充要条件D ．甲既不是乙的充分条件，也不是乙的必要条件解析：“甲⇒乙”，即“x ≠2或y ≠3⇒x ＋y ≠5”，其逆否命题为：“x ＋y ＝5”⇒“x ＝2且y ＝3”显然不正确．同理，可判断命题“乙⇒甲”为真命题．所以选B.答案：B11．定义：离心率e ＝5－12的椭圆为“黄金椭圆”．对于椭圆E ：x 2a 2＋y 2b2＝1(a >b >0)，如果a ，b ，c 不是等比数列，那么椭圆E ( ) A ．一定是“黄金椭圆” B ．一定不是“黄金椭圆” C ．可能是“黄金椭圆” D ．可能不是“黄金椭圆” 解析：假设E 为黄金椭圆，则有 e ＝ca ＝5－12，即c ＝5－12a .所以b 2＝a 2－c 2＝a 2－⎝ ⎛⎭⎪⎫5－12a 2＝5－12a 2＝ac ，这说明a ，b ，c 成等比数列，与已知矛盾，故椭圆E 一定不是“黄金椭圆”．故选B.答案：B12．若焦点在x 轴上的椭圆x 22＋y 2m ＝1的离心率为12，则m ＝( )A. 3B.32C.83D.23解析：假设m ＝32，则c 2＝2－32＝12，c ＝22，e ＝c a ＝12.故选B.答案：B13．若圆x 2＋y 2＝r 2上恰有相异两点到直线4x －3y ＋25＝0的距离等于1，则r 的取值范围是( )A ．[4,6]B ．[4,6)C ．(4,6]D ．(4,6)解析：因为圆心O (0,0)到直线4x －3y ＋25＝0的距离d ＝5，若r ＝4，则圆上只有一点到直线的距离等于1，故r ≠4.又若r ＝6，则圆上有三点到直线的距离等于1，故r ≠6.所以选D.答案：D14．对任意的锐角α、β，下列不等关系中正确的是( ) A ．sin(α＋β)>sin α＋sin β B ．sin(α＋β)>cos α＋cos β C ．cos(α＋β)<sin α＋sin β D ．cos(α＋β)<cos α＋cos β解析：当α＝β＝30°时，可排除A 、B 选项，当α＝β＝15°时，代入C 选项中，即0<cos30°<2sin15°，两边平方，34＝0.75<4sin 215°＝4×1－cos30°2＝2－3≈0.268矛盾．故选D.答案：D15．在△ABC 中，有命题：①AB →－AC →＝BC →；②AB →＋BC →＋CA →＝0；③若(AB →＋AC →)·(AB →－AC →)＝0，则△ABC 为等腰三角形；④若AC →·AB →>0，则△ABC 为锐角三角形．上述命题正确的是( )A ．①②B ．①④C ．②③D ．②③④解析：∵AB →－AC →＝CB →易知①错，②、③都正确．而AC →·AB →>0⇒|AC →||AB →|cos A >0⇒∠A 为锐角，不能断言△ABC 为锐角三角形，即④错．答案：C16．已知函数f (x )＝ax 2＋bx ＋c (a ，b ，c ∈R ，a <0)对于一切实数x ，f (1－x )＝f (1＋x )均成立，且f (－1)<0，f (0)>0.则有( )A ．a ＋b ＋c <0B ．b <a ＋cC ．c <2bD ．abc >0解析：(排除法)由题设可知抛物线的对称轴为x ＝1，即 －b2a ＝1，b ＝－2a >0.f (－1)＝a －b ＋c <0⇒a ＋c <b ，排除 B.f (1)＝a ＋b ＋c >0，排除A.a <0，f (0)＝c >0，b >0，排除D.另外选项C 的正确性可如下证明： a ＋c <b ⇒c <b －a <b －2a ＝2b . 答案：C17．对于函数①f (x )＝|x ＋2|；②f (x )＝(x －2)2；③f (x )＝cos(x －2)． 判断如下两个命题的真假：命题甲：f (x ＋2)是偶函数；命题乙：f (x )在(－∞，2)上是减函数，在(2，＋∞)上是增函数； 能使命题甲、乙均为真的所有函数的序号是( )A ．①②B ．①③C ．②D ．③解析：命题甲f (x ＋2)是偶函数，可知②③满足条件，排除①；作出②③函数的图象，可知③不满足命题乙的条件，所以选C.答案：C18．已知四边形ABCD 为菱形，点P 在对角线AC 上(不包括端点A 、C )，则AP →等于( )A ．λ(AB →＋AD →)，λ∈(0,1)B ．λ(AB →＋BC →)，λ∈⎝⎛⎭⎪⎫0，22 C ．λ(AB →－AD →)，λ∈(0,1)D ．λ(AB →－BC →)，λ∈⎝⎛⎭⎪⎫0，22 解析：λ(AB →＋AD →)＝λAC →，当λ∈(0,1)时，|λAC →|＝λ|AC →|∈(0，|AC →|)，而选项B 中λ(AB →＋BC →)∈⎝ ⎛⎭⎪⎪⎫0，22|AC →|，不满足条件，选项C 、D 则显然不正确，故选A.答案：A19．(2011·陕西模拟)如图所示，O ，A ，B 是平面上三点，向量OA →＝a ，OB →＝b .在平面AOB 上，P 是线段AB 垂直平分线上任意一点，向量OP →＝p ，且|a |＝3，|b |＝2，则p ·(a －b )的值是( )A ．5B.52 C ．3 D.32解析：因为P 是线段AB 垂直平分线上任意一点，不妨设P 为AB 的中点，则有OP →＝p ＝12(a ＋b )． ∴p ·(a －b )＝12(|a |2－|b |2)． ∵|a |＝3，|b |＝2，∴p ·(a －b )＝52. 答案：B20．在△ABC 中，已知D 是AB 边上一点，若AD →＝2DB →，CD →＝13CA →＋λCB →，则λ等于( ) A.23B.13 C ．－13D ．－23解析：取△ABC 为等腰三角形，如图所示，则有CD →＝CE →＋CF →，此时CE→＝13CA →，CF →＝23CB →，而CD →＝13CA →＋λCB →，故λ＝23. 答案：A。

高考专题训练十九特例检验型、逆向思维型、综合型班级_______ 姓名_______ 时间：45分钟分值：100分总得分_______1．（全国高考题）函数f(x)＝M sin(ωx＋φ)（ω〉0)在区间［a，b]上是增函数，且f(a）＝－M,f（b）＝M，则g(x）＝M cos（ωx＋φ)在[a,b]上（)A．是增函数B．是减函数C．可以取得最大值M D．可以取得最小值－M解析:此题单纯从“数"的角度去分析，具有相当的难度．若在同一直角坐标系中作出函数y＝M sin（ωx＋φ)和y＝M cos(ωx＋φ）的大致图形（如下图）,再观察在区间[a，b］上函数y＝M cos（ωx＋φ)图象的特征，则易知正确答案是C.答案：C2．（全国高考题）如果直线l将圆x2＋y2－2x－4y＝0平分，且不通过第四象限，那么l的斜率的取值范围是( ）A．［0,2］B．［0,1]C。

错误!D。

错误!解析:由题设，直线l平分圆，显然直线l应过圆心M（1，2)．设过M的直线l的斜率为k,当k＝0时，l不过第四象限，当l过原点即k＝2时，l亦不过第四象限，由下图不难看出,0≤k≤2时均符合题意,故选A.这是“以形助数”．答案：A3．(全国高考题)定义在(－∞，＋∞）上的奇函数f(x）为增函数，偶函数g（x)在区间[0，＋∞)的图象与f(x）的图象重合．设a〉b>0，给出下列不等式:①f（b）－f（－a)>g(a)－g（－b），②f（b）－f（－a)〈g(a)－g(－b）,③f（a)－f(－b）>g(b)－g（－a)，④f(a）－f（－b)<g(b)－g(－a）．其中成立的是（)A．①② B．②③C．①③ D．②④解析:依题意画出f（x）在［0，＋∞）上的示意图(如下图)从图中易得：由f(x）奇，g(x)偶有，f(a)＝g（a)＝g(－a）＝－f（－a），f（b)＝g（b)＝g（－b)＝－f（－b)，f(b)－f（－a）＝f(b）＋f（a）＝g（b)＋g(a)>g（a)－g(－b）,f(a）－f(－b)＝f(a)＋f（b)＝g(a)＋g(b）〉g（b）－g(－a）．故选C。

高考专题训练十九特例检验型、逆向思维型、综合型班级_______ 姓名_______ 时间：45分钟 分值：100分 总得分_______1．(全国高考题)函数f (x )＝M sin(ωx ＋φ)(ω>0)在区间[a ，b ]上是增函数，且f (a )＝－M ，f (b )＝M ，则g (x )＝M cos(ωx ＋φ)在[a ，b ]上( )A ．是增函数B ．是减函数C ．可以取得最大值MD ．可以取得最小值－M解析：此题单纯从“数”的角度去分析，具有相当的难度．若在同一直角坐标系中作出函数y ＝M sin(ωx ＋φ)和y ＝M cos(ωx ＋φ)的大致图形(如下图)，再观察在区间[a ，b ]上函数y ＝M cos(ωx ＋φ)图象的特征，则易知正确答案是C.答案：C2．(全国高考题)如果直线l 将圆x 2＋y 2－2x －4y ＝0平分，且不通过第四象限，那么l 的斜率的取值范围是( )A ．[0,2]B ．[0,1]C.⎣⎢⎡⎦⎥⎤0，12D.⎣⎢⎡⎭⎪⎫0，12 解析：由题设，直线l 平分圆，显然直线l 应过圆心M (1,2)．设过M 的直线l 的斜率为k ，当k ＝0时，l 不过第四象限，当l 过原点即k ＝2时，l 亦不过第四象限，由下图不难看出，0≤k ≤2时均符合题意，故选A.这是“以形助数”．答案：A3．(全国高考题)定义在(－∞，＋∞)上的奇函数f(x)为增函数，偶函数g(x)在区间[0，＋∞)的图象与f(x)的图象重合．设a>b>0，给出下列不等式：①f(b)－f(－a)>g(a)－g(－b)，②f(b)－f(－a)<g(a)－g(－b)，③f(a)－f(－b)>g(b)－g(－a)，④f(a)－f(－b)<g(b)－g(－a)．其中成立的是( )A．①②B．②③C．①③D．②④解析：依题意画出f(x)在[0，＋∞)上的示意图(如下图)从图中易得：由f(x)奇，g(x)偶有，f(a)＝g(a)＝g(－a)＝－f(－a)，f(b)＝g(b)＝g(－b)＝－f(－b)，f(b)－f(－a)＝f(b)＋f(a)＝g(b)＋g(a)>g(a)－g(－b)，f(a)－f(－b)＝f(a)＋f(b)＝g(a)＋g(b)>g(b)－g(－a)．故选C. 答案：C4．如果函数y ＝sin2x ＋a cos2x 的图象关于直线x ＝－π8对称，则实数a 的值为( ) A. 2 B ．－ 2 C ．1D ．－1分析：函数f (x )在x ＝－π8时取得最值；或考虑有f ⎝ ⎛⎭⎪⎫－π8＋x ＝f ⎝ ⎛⎭⎪⎫－π8－x 对一切x ∈R 恒成立．解析：解法一：设f (x )＝sin2x ＋a cos2x ，因为函数的图象关于直线x ＝－π8对称，所以f ⎝ ⎛⎭⎪⎫－π8＋x ＝f ⎝ ⎛⎭⎪⎫－π8－x 对一切实数x 都成立， 即sin2⎝ ⎛⎭⎪⎫－π8＋x ＋a cos2⎝ ⎛⎭⎪⎫－π8＋x＝sin2⎝ ⎛⎭⎪⎫－π8－x ＋a cos2⎝ ⎛⎭⎪⎫－π8－x 即sin ⎝ ⎛⎭⎪⎫－π4＋2x ＋sin ⎝ ⎛⎭⎪⎫π4＋2x ＝a ⎣⎢⎡⎦⎥⎤cos ⎝⎛⎭⎪⎫π4＋2x －cos ⎝ ⎛⎭⎪⎫－π4＋2x ，∴2sin2x ·cos π4＝－2a sin2x ·sin π4，即(a ＋1)·sin2x ＝0对一切实数x 恒成立，而sin2x 不能恒为0， ∴a ＋1＝0，即a ＝－1，故选D.解法二：∵f (x )＝sin2x ＋a cos2x 关于直线x ＝－π8对称．∴有f ⎝ ⎛⎭⎪⎫－π8＋x ＝f ⎝ ⎛⎭⎪⎫－π8－x 对一切x ∈R 恒成立． 特别，对于x ＝π8应该成立．将x ＝π8代入上式，得f (0)＝f ⎝ ⎛⎭⎪⎫－π4， ∴sin0＋a cos0＝sin ⎝ ⎛⎭⎪⎫－π2＋a cos ⎝ ⎛⎭⎪⎫－π2∴0＋a ＝－1＋a ×0. ∴a ＝－1.故选D.解法三：y ＝sin2x ＋a cos2x ＝1＋a 2sin(2x ＋φ)，其中角φ的终边经过点(1，a )．其图象的对称轴方程为2x ＋φ＝k π＋π2(k ∈Z)，即x ＝k π2＋π4－φ2(k ∈Z)． 令k π2＋π4－φ2＝－π8(k ∈Z)． 得φ＝k π＋3π4(k ∈Z)．但角φ的终边经过点(1，a )，故k 为奇数，角φ的终边与－π2角的终边相同，∴a ＝－1.故选D.解法四：y ＝sin2x ＋a cos2x ＝1＋a 2sin(2x ＋φ)，其中角φ满足tan φ＝a .因为f (x )的对称轴为y ＝－π8，∴当x ＝－π8时函数y ＝f (x )有最大值或最小值，所以1＋a 2＝f ⎝ ⎛⎭⎪⎫－π8或－1＋a 2＝f ⎝ ⎛⎭⎪⎫－π8，即1＋a 2＝sin ⎝ ⎛⎭⎪⎫－π4＋a cos ⎝ ⎛⎭⎪⎫－π4，或－1＋a 2＝sin ⎝ ⎛⎭⎪⎫－π4＋a cos ⎝ ⎛⎭⎪⎫－π4.解之得a ＝－1.故选D. 答案：D评析：本题给出了四种不同的解法，充分利用函数图象的对称性的特征来解题．解法一是运用了方程思想或恒等式思想求解．解法二是利用了数形结合的思想求解，抓住f (m ＋x )＝f (m －x )的图象关于直线x ＝m 对称的性质，取特殊值来求出待定系数a 的值．解法三利用函数y ＝A sin(ωx ＋φ)的对称轴是方程ωx ＋φ＝k π＋π2(k ∈Z)的解x ＝k π＋π2－φω(k ∈Z)，然后将x ＝－π8代入求出相应的φ值，再求a 的值．解法四利用对称轴的特殊性质，在此处函数f (x )取最大值或最小值．于是有f ⎝ ⎛⎭⎪⎫－π8＝[f (x )]max 或f ⎝ ⎛⎭⎪⎫－π8＝[f (x )]min .从而转化为解方程问题，体现了方程思想．由此可见，本题体现了丰富的数学思想方法，要从多种解法中悟出其实质东西．5．△ABC 的外接圆的圆心为O ，两条边上的高的交点为H ，OH →＝m (OA →＋OB →＋OC →)，则实数m 的值为( )A.12 B ．1 C ．2 D.22解析：当△ABC 为等腰直角三角形时，O 为AC 的中点，AB 、BC 边上高的交点H 与B 重合(如图)，OA →＋OB →＋OC →＝OB →＝OH →，所以m ＝1.答案：B6．设f (x )是定义在实数集R 上的任意一个增函数，且F (x )＝f (x )－f (－x )，那么F (x )应为( )A ．增函数且是奇函数B ．增函数且为偶函数C ．减函数且是奇函数D ．减函数且为偶函数解析：因为f (x )是定义在R 上的任意一个增函数，可取f (x )＝x ，知F (x )＝x －(－x )＝2x ，故选A.答案：A7．若sin α＋sin β＝13(cos β－cos α)，α、β∈(0，π)．则α－β的值为( )A ．－2π3B ．－π3C.π3D.2π3解析：由sin α＋sin β＝13(cos β－cos α)及α、β的范围，可直接推α－β的值，但运算量较大．令β＝π6代入，得sin α＝－13cos α，即tan α＝－33，α∈(0，π)，∴α＝5π6.∴α－β＝5π6－π6＝2π3，故选D.答案：D8．(全国高考题)若a >b >1，P ＝lg a · lg b ，Q ＝12(lg a ＋lg b )，R ＝lg ⎝ ⎛⎭⎪⎫a ＋b 2，则( ) A ．R <P <Q B ．P <Q <R C ．Q <P <RD ．P <R <Q解析：取a ＝100，b ＝10，则P ＝2，Q ＝1.5，R ＝lg 1102>lg 1002＝2－lg2>Q ，故应选B.答案：B9．若0<|α|<π4，则( )A ．sin2α>sin αB ．cos2α<cos αC ．tan2α>tan αD ．cot2α>cot α解析：取α＝±π6，可否定A 、C 、D ，因此选B.答案：B10．命题甲：x ≠2或y ≠3；命题乙：x ＋y ≠5，则( ) A ．甲是乙的充分不必要条件 B ．甲是乙的必要不充分条件 C ．甲是乙的充要条件D ．甲既不是乙的充分条件，也不是乙的必要条件解析：“甲⇒乙”，即“x ≠2或y ≠3⇒x ＋y ≠5”，其逆否命题为：“x ＋y ＝5”⇒“x ＝2且y ＝3”显然不正确．同理，可判断命题“乙⇒甲”为真命题．所以选B.答案：B11．定义：离心率e ＝5－12的椭圆为“黄金椭圆”．对于椭圆E ：x 2a 2＋y2b 2＝1(a >b >0)，如果a ，b ，c 不是等比数列，那么椭圆E ( )A ．一定是“黄金椭圆”B ．一定不是“黄金椭圆”C ．可能是“黄金椭圆”D ．可能不是“黄金椭圆”解析：假设E 为黄金椭圆，则有e ＝c a ＝5－12，即c ＝5－12a . 所以b 2＝a 2－c 2＝a 2－⎝ ⎛⎭⎪⎫5－12a 2＝5－12a 2＝ac ， 这说明a ，b ，c 成等比数列，与已知矛盾，故椭圆E 一定不是“黄金椭圆”．故选B. 答案：B12．若焦点在x 轴上的椭圆x 22＋y 2m ＝1的离心率为12，则m ＝( )A. 3B.32C.83D.23解析：假设m ＝32，则c 2＝2－32＝12，c ＝22，e ＝c a ＝12.故选B.答案：B13．若圆x 2＋y 2＝r 2上恰有相异两点到直线4x －3y ＋25＝0的距离等于1，则r 的取值范围是( )A ．[4,6]B ．[4,6)C ．(4,6]D ．(4,6)解析：因为圆心O (0,0)到直线4x －3y ＋25＝0的距离d ＝5，若r ＝4，则圆上只有一点到直线的距离等于1，故r ≠4.又若r ＝6，则圆上有三点到直线的距离等于1，故r ≠6.所以选D.答案：D14．对任意的锐角α、β，下列不等关系中正确的是( ) A ．sin(α＋β)>sin α＋sin β B ．sin(α＋β)>cos α＋cos β C ．cos(α＋β)<sin α＋sin β D ．cos(α＋β)<cos α＋cos β解析：当α＝β＝30°时，可排除A 、B 选项，当α＝β＝15°时，代入C 选项中，即0<cos30°<2sin15°，两边平方，34＝0.75<4sin 215°＝4×1－cos30°2＝2－3≈0.268矛盾．故选D.答案：D15．在△ABC 中，有命题：①AB →－AC →＝BC →；②AB →＋BC →＋CA →＝0；③若(AB →＋AC →)·(AB →－AC →)＝0，则△ABC 为等腰三角形；④若AC →·AB →>0，则△ABC 为锐角三角形．上述命题正确的是( )A ．①②B ．①④C ．②③D ．②③④解析：∵AB →－AC →＝CB →易知①错，②、③都正确．而AC →·AB →>0⇒|AC →||AB →|cos A >0⇒∠A 为锐角，不能断言△ABC 为锐角三角形，即④错．答案：C16．已知函数f (x )＝ax 2＋bx ＋c (a ，b ，c ∈R ，a <0)对于一切实数x ，f (1－x )＝f (1＋x )均成立，且f (－1)<0，f (0)>0.则有( )A ．a ＋b ＋c <0B ．b <a ＋cC ．c <2bD ．abc >0解析：(排除法)由题设可知抛物线的对称轴为x ＝1，即 －b2a＝1，b ＝－2a >0.f (－1)＝a －b ＋c <0⇒a ＋c <b ，排除 B.f (1)＝a ＋b ＋c >0，排除A.a <0，f (0)＝c >0，b >0，排除D.另外选项C 的正确性可如下证明：a ＋c <b ⇒c <b －a <b －2a ＝2b .答案：C17．对于函数①f (x )＝|x ＋2|；②f (x )＝(x －2)2；③f (x )＝cos(x －2)． 判断如下两个命题的真假： 命题甲：f (x ＋2)是偶函数；命题乙：f (x )在(－∞，2)上是减函数，在(2，＋∞)上是增函数； 能使命题甲、乙均为真的所有函数的序号是( ) A ．①② B ．①③ C ．②D ．③解析：命题甲f (x ＋2)是偶函数，可知②③满足条件，排除①；作出②③函数的图象，可知③不满足命题乙的条件，所以选C.答案：C18．已知四边形ABCD 为菱形，点P 在对角线AC 上(不包括端点A 、C )，则AP →等于( ) A ．λ(AB →＋AD →)，λ∈(0,1)B ．λ(AB →＋BC →)，λ∈⎝ ⎛⎭⎪⎫0，22C ．λ(AB →－AD →)，λ∈(0,1) D ．λ(AB →－BC →)，λ∈⎝⎛⎭⎪⎫0，22解析：λ(AB →＋AD →)＝λAC →，当λ∈(0,1)时，|λAC →|＝λ|AC →|∈(0，|AC →|)，而选项B 中λ(AB →＋BC →)∈⎝ ⎛⎭⎪⎫0，22|AC →|，不满足条件，选项C 、D则显然不正确，故选A.答案：A19．(2011·陕西模拟)如图所示，O ，A ，B 是平面上三点，向量OA →＝a ，OB →＝b .在平面AOB 上，P 是线段AB 垂直平分线上任意一点，向量OP →＝p ，且|a |＝3，|b |＝2，则p ·(a －b )的值是( )A ．5 B.52 C ．3D.32解析：因为P 是线段AB 垂直平分线上任意一点，不妨设P 为AB 的中点，则有OP →＝p ＝12(a ＋b )．∴p ·(a －b )＝12(|a |2－|b |2)．∵|a |＝3，|b |＝2， ∴p ·(a －b )＝52.答案：B20．在△ABC 中，已知D 是AB 边上一点，若AD →＝2DB →，CD →＝13CA →＋λCB →，则λ等于( )A.23B.13C ．－13D ．－23解析：取△ABC 为等腰三角形，如图所示，则有CD →＝CE →＋CF →，此时CE →＝13CA →，CF →＝23CB →，而CD →＝13CA →＋λCB →，故λ＝23. 答案：A。