试卷03

03 四年级语文上册期末教学质量检测试卷部编版(时间：90分钟 满分：100分)一、请用“√”给加点字选择正确的读音。

(4分)琵琶．(p á b á) 憧．(c ōng ch ōng)憬 打盹．(t ǔn d ǔn) 人声鼎．(d ǐng t ǐng)沸 躯．(x ū q ū)干 诀窍．(qi ào xi ào) 荧．(y íng y ín)屏 富丽堂皇．(hu áng h áng) 二、读拼音，把词语规范地写在田字格里。

（8分）zhu āng ji ɑ m ǎn y ì zh ú ji àn ch éng d ùy án ji ū p ú t ɑo h ú di é ch āo gu ò三、按要求，写词语。

（9分）胖乎乎（ABB 式）:____________ ____________ ____________ 自言自语（ABAC 式）：____________ ____________ ____________ 果实累累（ABCC 式）：____________ ____________ ____________ 四、给下列字加上不同的偏旁变成新字，完成词语。

(6分)【者】 ( )名 ( )博 ( )塞 肥( ) 【交】 比( ) ( )猾 ( )游 ( )子 【莫】 日( ) 闭( ) 坟( ) 冷( ) 五、把下列词语补充完整，并完成练习。

(13分)①呼( )唤( ) ②上( )入( ) ③( )( )不入 ④( )( )喧天 ⑤人声( )( ) ⑥( )( )妙算1.含有近义词的词语是______，含有反义词的词语是______。

(填序号)我能写两个既含近义词又含反义词的词语：____________、______________。

小升初数学模拟试卷（03）一、填空题。

（20分，每空1分）1．要记录某市城区某一天气温变化情况，应选用( )统计图。

2.把256,2.65%,2.65·,2.6·5·按照从小到大的顺序排列是( )<( )<( )<( )。

3.园林工人在长96米的公路两边每隔6米栽一棵树（首尾都栽），现在要改成每隔4米栽一棵树，那么不用移栽的树有( ) 棵．4.（ ）的倒数是1 ，1.2的倒数是（ ），最小合数的倒数是（ ）．5.制作 这样10张卡片，想一想，至少要抽出（ ）张卡片才能保证既有偶数又有奇数？试一试6.把5份快餐分给4个工人，有一个人至少得到（ ）份．7.从1﹣24中至少取出（ ）个数，才能保证其中有两个数的差是5的倍数．8.时钟6点敲6下，10秒敲完；10点敲10下，（ ）秒敲完。

9.如图，把一个圆柱体切拼成一个长方体，表面积比原来增加了24平方厘米，已知底面的半径是2厘米，相信你一定能求出圆柱体的体积是（ ）立方厘米．10．明明读一本320页的书，第一天读了这本书的，第二天应从第（ ）页开始读．11．用150厘米长的铁丝做一个长方形的框架．长与宽的比是3：2，这个长方形的长是（ ）厘米，宽是（ ）厘米．12．妈妈准备了7只信封，在每只信封里都放了钱共100元，要求每一只信封里都放整元数，而且都不相同，那么钱放得最多的一只信封里至少放（ ）元？13．在信息时代，信息安全十分重要，往往需要对信息进行加密，若按照“叠3加1取个位”的方式逐位加密，明码“16”加密之后的密码为“49”，若某个四位明码按照上述加密方式，经过两次加密得到的密码是“2445”，则明码是（ ）14.晨光小学进行一次体育测试，合格的有108人，不合格的有12人。

这次体育测试的合格率是（ ）。

二、选择题。

（10分，每小题2分）1.某市政公司进行路灯改造，其排列规律是 ，第100盏路灯应是（ ）色。

上学期期末教学质量监测 六年级英语试卷03考生注意：1.考试时间60分钟。

2.全卷共九道大题，总共100分。

听力（30分） 笔试（70分） 总 分 题号 一二三四五六七八九十 十一十二 十三 得分听力部分一、听句子，选出正确的答案。

（5分，每小题1分）( )1.A. It's blue. B. It's my desk. C. It's small. ( )2.A. OK. B. Thank you. C. No, not very good. ( )3. A. They are dogs. B.Yes, they are. C.They are my dogs. ( )4. A. Sounds good. B. I like tomatoes. C. Yes, I do. ( )5. A. It's a model plane. B. This is yours. C. It's under the chair. 二、听对话及问题，选择最佳答案。

（5分，每小题1分）( )1. A. Alice. B. Alan. C. Eric.( )2.A. Yes, he is. B. No, he isn't. C. We don't know. ( )3. A. It's on the bag. B.It's in the bag. C. It's in the box ( )4. A. At the school. B. In a store. C. At home. ( )5. A. Hamburgers. B. Vegetables. C. We don't know. 三、听录音, 补全句子。

(10分，每小题2分)1.—What do you do on the weekend? —I _____________________.2.—Whe n is Mike’s birthday? — It’s in _________________.3.—Do you_________________on Tuesday? —Yes, I do.本考场试卷序号 （由监考填写）4. Zhang Peng often_______________.5. I usually ____________at 6:30.四、听短文，判断正误(对的写T,错的写F)。

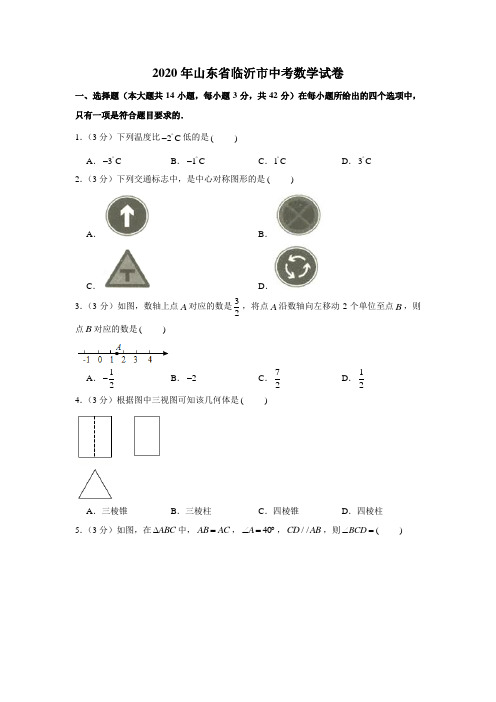
2020年山东省临沂市中考数学试卷一、选择题（本大题共14小题，每小题3分，共42分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（3分）下列温度比2C ︒-低的是( ) A ．3C ︒-B ．1C ︒-C ．1C ︒D ．3C ︒2．（3分）下列交通标志中，是中心对称图形的是( )A ．B ．C ．D ．3．（3分）如图，数轴上点A 对应的数是32，将点A 沿数轴向左移动2个单位至点B ，则点B 对应的数是( )A ．12-B ．2-C ．72D ．124．（3分）根据图中三视图可知该几何体是( )A ．三棱锥B ．三棱柱C ．四棱锥D ．四棱柱5．（3分）如图，在ABC ∆中，AB AC =，40A ∠=︒，//CD AB ，则(BCD ∠= )A ．40︒B ．50︒C ．60︒D ．70︒6．（3分）计算322(2)a a -÷的结果是( ) A ．32a -B ．42a -C ．34aD ．44a7．（3分）设72a ．则( ) A ．23a <<B ．34a <<C ．45a <<D ．56a <<8．（3分）一元二次方程2480x x --=的解是( ) A ．1223x =-+，2223x =--B ．1223x =+2223x =-C ．1222x =+2222x =-D ．123x =，223x =-9．（3分）从马鸣、杨豪、陆畅、江宽四人中抽调两人参加“寸草心”志愿服务队，恰好抽到马鸣和杨豪的概率是( ) A ．112 B ．18C ．16D ．1210．（3分）《孙子算经》是中国古代重要的数学著作，成书大约在一千五百年前，其中一道题，原文是：“今三人共车，两车空；二人共车，九人步．问人与车各几何？”意思是：现有若干人和车，若每辆车乘坐3人，则空余两辆车；若每辆车乘坐2人，则有9人步行．问人与车各多少？设有x 人，y 辆车，可列方程组为( ) A ．2392xy x y ⎧=+⎪⎪⎨⎪+=⎪⎩B ．2392xy x y ⎧=-⎪⎪⎨-⎪=⎪⎩C ．2392xy x y ⎧=+⎪⎪⎨-⎪=⎪⎩D ．2392xy x y ⎧=-⎪⎪⎨⎪-=⎪⎩11．（3分）如图是甲、乙两同学五次数学测试成绩的折线图．比较甲、乙的成绩，下列说法正确的是( )A ．甲平均分高，成绩稳定B ．甲平均分高，成绩不稳定C ．乙平均分高，成绩稳定D ．乙平均分高，成绩不稳定12．（3分）如图，P 是面积为S 的ABCD 内任意一点，PAD ∆的面积为1S ，PBC ∆的面积为2S ，则( )A ．122SS S +> B ．122S S S +<C ．122SS S +=D ．12S S +的大小与P 点位置有关13．（3分）计算11x yx y ---的结果为( ) A ．(1)(1)x yx y -+--B ．(1)(1)x yx y ---C ．(1)(1)x yx y ----D ．(1)(1)x yx y +--14．（3分）如图，在O 中，AB 为直径，80AOC ∠=︒．点D 为弦AC 的中点，点E 为BC 上任意一点．则CED ∠的大小可能是( )A ．10︒B ．20︒C ．30︒D ．40︒二、填空题（本大题共5小题，每小题3分，共15分） 15．（3分）不等式210x +<的解集是 ．16．（3分）若1a b +=，则2222a b b -+-= ．17．（3分）点1(2-，)m 和点(2,)n 在直线2y x b =+上，则m 与n 的大小关系是 ．18．（3分）如图，在ABC ∆中，D 、E 为边AB 的三等分点，////EF DG AC ，H 为AF 与DG 的交点．若6AC =，则DH = ．19．（3分）我们知道，两点之间线段最短，因此，连接两点间线段的长度叫做两点间的距离；同理，连接直线外一点与直线上各点的所有线段中，垂线段最短，因此，直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．类似地，连接曲线外一点与曲线上各点的所有线段中，最短线段的长度，叫做点到曲线的距离．依此定义，如图，在平面直角坐标系中，点(2,1)A 到以原点为圆心，以1为半径的圆的距离为 ．三、解答题（本大题共7小题，共63分）20．（72112()sin 603226--︒． 21．（7分）2020年是脱贫攻坚年．为实现全员脱贫目标，某村贫困户在当地政府支持帮助下，办起了养鸡场．经过一段时间精心饲养，总量为3000只的一批鸡可以出售．现从中随机抽取50只，得到它们质量的统计数据如下：质量/kg组中值 频数（只)0.9 1.1x < 1.0 6 1.1 1.3x < 1.2 91.3 1.5x <1.4a1.5 1.7x < 1.6 15 1.7 1.9x <1.88根据以上信息，解答下列问题：（1）表中a = ，补全频数分布直方图； （2）这批鸡中质量不小于1.7kg 的大约有多少只？（3）这些贫困户的总收入达到54000元，就能实现全员脱贫目标．按15元/kg 的价格售出这批鸡后，该村贫困户能否脱贫？22．（7分）如图，要想使人安全地攀上斜靠在墙面上的梯子的顶端，梯子与地面所成的角α般要满足6075α︒︒，现有一架长5.5m 的梯子．（1）使用这架梯子最高可以安全攀上多高的墙（结果保留小数点后一位）？（2）当梯子底端距离墙面2.2m 时，α等于多少度（结果保留小数点后一位）？此时人是否能够安全使用这架梯子？（参考数据：sin750.97︒≈，cos750.26︒≈，tan75 3.73︒≈，sin23.60.40︒≈，cos66.40.40︒≈，tan21.80.40︒≈．)23．（9分）已知蓄电池的电压为定值，使用蓄电池时，电流I （单位：)A 与电阻R （单位：)Ω是反比例函数关系．当4R =Ω时，9I A =．（1）写出I 关于R 的函数解析式；（2）完成下表，并在给定的平面直角坐标系中画出这个函数的图象；/R Ω ⋯ ⋯ /I A ⋯⋯（3）如果以此蓄电池为电源的用电器的限制电流不能超过10A ，那么用电器可变电阻应控制在什么范围内？24．（9分）已知1O 的半径为1r ，2O 的半径为2r ．以1O 为圆心，以12r r +的长为半径画弧，再以线段12O O 的中点P 为圆心，以1212O O 的长为半径画弧，两弧交于点A ，连接1O A ，2O A ，1O A 交1O 于点B ，过点B 作2O A 的平行线BC 交12O O 于点C ．（1）求证：BC 是2O 的切线；（2）若12r =，21r =，126O O =，求阴影部分的面积．25．（11分）已知抛物线22232(0)y ax ax a a =--+≠． （1）求这条抛物线的对称轴；（2）若该抛物线的顶点在x 轴上，求其解析式；（3）设点1(,)P m y ，2(3,)Q y 在抛物线上，若12y y <，求m 的取值范围．26．（13分）如图，菱形ABCD 的边长为1，60ABC ∠=︒，点E 是边AB 上任意一点（端点除外），线段CE 的垂直平分线交BD ，CE 分别于点F ，G ，AE ，EF 的中点分别为M ，N ．（1）求证：AF EF =； （2）求MN NG +的最小值；（3）当点E 在AB 上运动时，CEF ∠的大小是否变化？为什么？2020年山东省临沂市中考数学试卷参考答案与试题解析一、选择题（本大题共14小题，每小题3分，共42分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（3分）下列温度比2C ︒-低的是( ) A ．3C ︒-B ．1C ︒-C ．1C ︒D ．3C ︒【解答】解：根据两个负数，绝对值大的反而小可知32-<-， 所以比2C ︒-低的温度是3C ︒-． 故选：A ．2．（3分）下列交通标志中，是中心对称图形的是( )A ．B ．C ．D ．【解答】解：A 、不是中心对称图形，不符合题意；B 、是中心对称图形，符合题意；C 、不是中心对称图形，不符合题意；D 、不是中心对称图形，不符合题意．故选：B ．3．（3分）如图，数轴上点A 对应的数是32，将点A 沿数轴向左移动2个单位至点B ，则点B 对应的数是( )A ．12-B ．2-C ．72D ．12【解答】解：点A 向左移动2个单位， 点B 对应的数为：31222-=-． 故选：A ．4．（3分）根据图中三视图可知该几何体是( )A ．三棱锥B ．三棱柱C ．四棱锥D ．四棱柱【解答】解：根据图中三视图可知该几何体是三棱柱． 故选：B ．5．（3分）如图，在ABC ∆中，AB AC =，40A ∠=︒，//CD AB ，则(BCD ∠= )A ．40︒B ．50︒C ．60︒D ．70︒【解答】解：在ABC ∆中，AB AC =，40A ∠=︒，70ACB ∴∠=︒， //CD AB ，180140ACD A ∴∠=︒-∠=︒， 70BCD ACD ACB ∴∠=∠-∠=︒．故选：D ．6．（3分）计算322(2)a a -÷的结果是( )A ．32a -B ．42a -C ．34aD ．44a【解答】解：原式624a a =÷ 44a =．故选：D ．7．（3分）设72a ．则( )A ．23a <<B ．34a <<C ．45a <<D ．56a <<【解答】解：273<<，4725∴<+<，45a ∴<<．故选：C ．8．（3分）一元二次方程2480x x --=的解是( ) A ．1223x =-+，2223x =-- B ．1223x =+，2223x =-C ．1222x =+，2222x =-D ．123x =，223x =-【解答】解：一元二次方程2480x x --=， 移项得：248x x -=，配方得：24412x x -+=，即2(2)12x -=，开方得：223x -=±，解得：1223x =+，2223x =-． 故选：B ．9．（3分）从马鸣、杨豪、陆畅、江宽四人中抽调两人参加“寸草心”志愿服务队，恰好抽到马鸣和杨豪的概率是( ) A ．112 B ．18C ．16D ．12【解答】解：根据题意画图如下：共有12种等可能情况数，其中恰好抽到马鸣和杨豪的有2种， 则恰好抽到马鸣和杨豪的概率是21126=； 故选：C ．10．（3分）《孙子算经》是中国古代重要的数学著作，成书大约在一千五百年前，其中一道题，原文是：“今三人共车，两车空；二人共车，九人步．问人与车各几何？”意思是：现有若干人和车，若每辆车乘坐3人，则空余两辆车；若每辆车乘坐2人，则有9人步行．问人与车各多少？设有x人，y辆车，可列方程组为()A．2 392xyxy ⎧=+⎪⎪⎨⎪+=⎪⎩B．2392xyxy⎧=-⎪⎪⎨-⎪=⎪⎩C．2392xyxy⎧=+⎪⎪⎨-⎪=⎪⎩D．2392xyxy⎧=-⎪⎪⎨⎪-=⎪⎩【解答】解：依题意，得：2392xyxy⎧=-⎪⎪⎨-⎪=⎪⎩．故选：B．11．（3分）如图是甲、乙两同学五次数学测试成绩的折线图．比较甲、乙的成绩，下列说法正确的是()A．甲平均分高，成绩稳定B．甲平均分高，成绩不稳定C．乙平均分高，成绩稳定D．乙平均分高，成绩不稳定【解答】解：10085908095905x++++==乙，8590808580845x++++==甲，因此乙的平均数较高；2_S乙，2_S甲，5014>，∴乙的离散程度较高，不稳定，甲的离散程度较低，比较稳定；故选：D．12．（3分）如图，P 是面积为S 的ABCD 内任意一点，PAD ∆的面积为1S ，PBC ∆的面积为2S ，则( )A ．122SS S +>B ．122S S S +<C ．122SS S +=D ．12S S +的大小与P 点位置有关【解答】解：过点P 作EF AD ⊥交AD 于点E ，交BC 于点F ， 四边形ABCD 是平行四边形，AD BC ∴=， S BC EF ∴=，12AD PE S =，22BC PFS =， EF PE PF =+，AD BC =， 122SS S ∴+=， 故选：C ．13．（3分）计算11x yx y ---的结果为( ) A ．(1)(1)x yx y -+--B ．(1)(1)x yx y ---C ．(1)(1)x yx y ----D ．(1)(1)x yx y +--【解答】解：原式(1)(1)(1)(1)(1)(1)x y y x x y x y --=----- (1)(1)xy x xy yx y --+=--(1)(1)x yx y -+=--．故选：A ．14．（3分）如图，在O 中，AB 为直径，80AOC ∠=︒．点D 为弦AC 的中点，点E 为BC 上任意一点．则CED ∠的大小可能是( )A ．10︒B ．20︒C ．30︒D ．40︒【解答】解：连接OD 、OE ，OC OA =，OAC ∴∆是等腰三角形，点D 为弦的中点，40DOC ∴∠=︒，100BOC ∠=︒，设BOE x ∠=，则100COE x ∠=︒-，10040DOE x ∠=︒-+︒，OC OE =，100COE x ∠=︒-， 1402OEC OCE x ∴∠=∠=︒+，OD OE <，10040140DOE x x ∠=︒-+︒=︒-， 1202OED x ∴∠<︒+，11(40)(20)2022CED OEC OED x x ∴∠=∠-∠>︒+-︒+=︒，40CED ABC ∠<∠=︒， 2040CED ∴︒<∠<︒故选：C ．二、填空题（本大题共5小题，每小题3分，共15分） 15．（3分）不等式210x +<的解集是 12x <- ． 【解答】解：移项，得：21x <-， 系数化为1，得：12x <-， 故答案为12x <-． 16．（3分）若1a b +=，则2222a b b -+-= 1- ．【解答】解：1a b +=， 2222a b b ∴-+- ()()22a b a b b =+-+-22a b b =-+- 2a b =+- 12=- 1=-．故答案为：1-．17．（3分）点1(2-，)m 和点(2,)n 在直线2y x b =+上，则m 与n 的大小关系是 m n < ．【解答】解：直线2y x b =+中，20k =>，∴此函数y 随着x 的增大而增大，122-<， m n ∴<．故答案为m n <．18．（3分）如图，在ABC ∆中，D 、E 为边AB 的三等分点，////EF DG AC ，H 为AF 与DG 的交点．若6AC =，则DH = 1 ．【解答】解：D 、E 为边AB 的三等分点，////EF DG AC ，BE DE AD ∴==，BF GF CG ==，AH HF =，3AB BE ∴=，DH 是AEF ∆的中位线， 12DH EF ∴=，//EF AC ， BEF BAC ∴∆∆∽， ∴EF BE AC AB =，即63EF BEBE=， 解得：2EF =，112122DH EF ∴==⨯=，故答案为：1．19．（3分）我们知道，两点之间线段最短，因此，连接两点间线段的长度叫做两点间的距离；同理，连接直线外一点与直线上各点的所有线段中，垂线段最短，因此，直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．类似地，连接曲线外一点与曲线上各点的所有线段中，最短线段的长度，叫做点到曲线的距离．依此定义，如图，在平面直角坐标系中，点(2,1)A 到以原点为圆心，以1为半径的圆的距离为51- ．【解答】解：连接AO 交O 于B ，则线段AB 的长度即为点(2,1)A 到以原点为圆心，以1为半径的圆的距离， 点(2,1)A ，22215OA ∴=+=，1OB =， 51AB ∴=-，即点(2,1)A 到以原点为圆心，以1为半径的圆的距离为51-， 故答案为：51-．三、解答题（本大题共7小题，共63分）20．（7sin 60-︒．【解答】解：原式1123=-+16=+=． 21．（7分）2020年是脱贫攻坚年．为实现全员脱贫目标，某村贫困户在当地政府支持帮助下，办起了养鸡场．经过一段时间精心饲养，总量为3000只的一批鸡可以出售．现从中随机抽取50只，得到它们质量的统计数据如下：1.1 1.3x < 1.3 1.5x < 1.5 1.7x < 1.7 1.9x <根据以上信息，解答下列问题：（1）表中a = 12 ，补全频数分布直方图； （2）这批鸡中质量不小于1.7kg 的大约有多少只？（3）这些贫困户的总收入达到54000元，就能实现全员脱贫目标．按15元/kg 的价格售出这批鸡后，该村贫困户能否脱贫？【解答】解：（1）508159612a =----=（只)，补全频数分布直方图； 故答案为：12； （2）8300048050⨯=（只) 答：这批鸡中质量不小于1.7kg 的大约有480只； （3）16 1.29 1.412 1.615 1.881.4450x ⨯+⨯+⨯+⨯+⨯==（千克）， 1.443000156480054000⨯⨯=>， ∴能脱贫，答：该村贫困户能脱贫．22．（7分）如图，要想使人安全地攀上斜靠在墙面上的梯子的顶端，梯子与地面所成的角α般要满足6075α︒︒，现有一架长5.5m 的梯子．（1）使用这架梯子最高可以安全攀上多高的墙（结果保留小数点后一位）？（2）当梯子底端距离墙面2.2m 时，α等于多少度（结果保留小数点后一位）？此时人是否能够安全使用这架梯子？（参考数据：sin750.97︒≈，cos750.26︒≈，tan75 3.73︒≈，sin23.60.40︒≈，cos66.40.40︒≈，tan21.80.40︒≈．)【解答】解：（1）由题意得，当75α=︒时，这架梯子可以安全攀上最高的墙， 在Rt ABC ∆中，sin ACABα=， sin 5.50.97 5.3AC AB α∴=≈⨯≈，答：使用这架梯子最高可以安全攀上5.3m 的墙； （2）在Rt ABC ∆中，cos 0.4BCABα==， 则66.4α≈︒，6066.475︒︒︒，∴此时人能够安全使用这架梯子．23．（9分）已知蓄电池的电压为定值，使用蓄电池时，电流I （单位：)A 与电阻R （单位：)Ω是反比例函数关系．当4R =Ω时，9I A =．（1）写出I 关于R 的函数解析式；（2）完成下表，并在给定的平面直角坐标系中画出这个函数的图象；/R Ω ⋯ 3 ⋯ /I A ⋯⋯（3）如果以此蓄电池为电源的用电器的限制电流不能超过10A ，那么用电器可变电阻应控制在什么范围内？【解答】解：（1）电流I 是电阻R 的反比例函数，设kI R=， 4R =Ω时，9I A = 94k ∴=， 解得4936k =⨯=，36I R∴=；（2）列表如下： /R Ω 3 4 5 6 8 9 10 12 /I A1297.264.543.63（3）10I ，36I R=， ∴3610R， 3.6R ∴，即用电器可变电阻应控制在不低于3.6欧的范围内．24．（9分）已知1O 的半径为1r ，2O 的半径为2r ．以1O 为圆心，以12r r +的长为半径画弧，再以线段12O O 的中点P 为圆心，以1212O O 的长为半径画弧，两弧交于点A ，连接1O A ，2O A ，1O A 交1O 于点B ，过点B 作2O A 的平行线BC 交12O O 于点C ．（1）求证：BC 是2O 的切线；（2）若12r =，21r =，126O O =，求阴影部分的面积．【解答】（1）证明：连接AP ，以线段12O O 的中点P 为圆心，以1212O O 的长为半径画弧， 121212O P AP O P O O ∴===， 1290O AO ∴∠=︒，2//BC O A ，11290O BC O AO ∴∠=∠=︒，过点2O 作2O D BC ⊥交BC 的延长线于点D ，∴四边形2ABDO 是矩形，2AB O D ∴=，112O A r r =+，22O D r ∴=，BC ∴是2O 的切线；（2）解：12r =，21r =，126O O =，11212O A O O ∴=， 160BO C ∴∠=︒，1124O C O B ∴==，2222114223BC OC O B ∴=-=-=， 1122216011602222323236023603O BC BO E r S S S O B BC πππ⨯⨯⨯∴=-=⋅-=⨯⨯=阴影扇形． 25．（11分）已知抛物线22232(0)y ax ax a a =--+≠．（1）求这条抛物线的对称轴；（2）若该抛物线的顶点在x 轴上，求其解析式；（3）设点1(,)P m y ，2(3,)Q y 在抛物线上，若12y y <，求m 的取值范围．【解答】解：（1）抛物线2222232(1)23y ax ax a a x a a =--+=-+--． ∴抛物线的对称轴为直线1x =；（2）抛物线的顶点在x 轴上，2230a a ∴--=， 解得32a =或1a =-， ∴抛物线为233322y x x =-+或221y x x =-+-； （3）抛物线的对称轴为1x =，则2(3,)Q y 关于1x =对称点的坐标为2(1,)y -，∴当0a >，13m -<<时，12y y <；当0a <，1m <-或3m >时，12y y <．26．（13分）如图，菱形ABCD 的边长为1，60ABC ∠=︒，点E 是边AB 上任意一点（端点除外），线段CE 的垂直平分线交BD ，CE 分别于点F ，G ，AE ，EF 的中点分别为M ，N ．（1）求证：AF EF =；（2）求MN NG +的最小值；（3）当点E 在AB 上运动时，CEF ∠的大小是否变化？为什么？【解答】解：（1）连接CF ，FG 垂直平分CE ，CF EF ∴=，四边形ABCD 为菱形，A ∴和C 关于对角线BD 对称，CF AF ∴=，AF EF ∴=；（2）连接AC ， M 和N 分别是AE 和EF 的中点，点G 为CE 中点， 12MN AF ∴=，12NG CF =，即1()2MN NG AF CF +=+， 当点F 与菱形ABCD 对角线交点O 重合时， AF CF +最小，即此时MN NG +最小， 菱形ABCD 边长为1，60ABC ∠=︒， ABC ∴∆为等边三角形，1AC AB ==， 即MN NG +的最小值为12；（3）不变，理由是：延长EF ，交DC 于H ，CFH FCE FEC ∠=∠+∠，AFH FAE FEA ∠=∠+∠， AFC FCE FEC FAE FEA ∴∠=∠+∠+∠+∠， 点F 在菱形ABCD 对角线BD 上，根据菱形的对称性可得：12AFD CFD AFC ∠=∠=∠， AF CF EF ==，AEF EAF ∴∠=∠，FEC FCE ∠=∠，AFD FAE ABF FAE CEF ∴∠=∠+∠=∠+∠， ABF CEF ∴∠=∠，60ABC ∠=︒，30ABF CEF ∴∠=∠=︒，为定值．。

数学人教版6年级上册第3单元单元专题卷03一、选择题1．人工饲养的狮子通常可以活到20岁，豹的寿命约是狮子寿命的34，狗的寿命约是豹寿命的45。

狗的寿命是多少岁？正确的列式是（ ）。

A ．342045⨯⨯B ．342045⨯÷C ．342045÷÷2．一个果园种了240棵桃树，比种的梨树多15，梨树种了多少棵？列式正确的是（ ）。

A ．240×15B ．240×（1＋15）C ．240÷（1＋15）3．甲数的23等于乙数的56（甲、乙两数都大于0），甲、乙两数相比较，（ ）。

A ．甲数＞乙数B ．甲数＝乙数C ．甲数＜乙数D ．无法确定大小关系4．一批零件，师傅比徒弟多加工了35，徒弟比师傅少加工15个，徒弟加工了（ ）个。

A ．9B ．12C ．255．一条路长20千米，甲队单独做4天完成，乙队单独做6天完成。

两队合做几天可以完成工程的110。

正确的列式是（ ）。

A ．1111046÷B ．201146÷＋C ．1111046⨯（＋）D ．110÷204206÷÷（＋）6．体积相等的冰和水，冰的质量比水的质量少110。

现有一块重8kg 的冰，如果一桶水的体积和这块冰的体积相等，这桶水有多重？正确的算式是（ ）。

A ．8÷（1－110）B ．8÷110C ．8÷（1＋110）D ．110＋8×1107．下面各情境中的问题，不能用算式12×23解决的是（ ）。

A ．一堆沙子12吨，运走了23，运走了多少吨沙子？B ．花圃里有玫瑰花12盆，百合花比玫瑰花多23，百合花比玫瑰花多多少盆？C ．一袋大米剩23，重12千克，这袋大米重多少千克？D ．弟弟有12元钱，买笔记本花去全部钱的23，买笔记本花了多少元钱？8．下面算式中，符合下图图意的算式是（ ）。

一、填空题（1）在绘制直线时按住( Shift )键，可绘制出与水平成45°的线段。

（2）绘制椭圆时，在拖动鼠标时按住( Shift )键，可以绘制出一个正圆。

（3）用点选方式选择多个图形的方法是：单击选取一个图形，然后按住( Shift )键，再单击其他图形即可选中多个图形。

（4）在混色器中可以为图形填充纯色、线性渐变色和( 放射状渐变 )。

（5）按( Ctrl+Z )键可以撤消前面的操作。

（6）橡皮擦工具只能对( 形状 )进行擦除，对文字和位图无效，如果要擦除文字或位图，必须将它们( 打散 )。

（7）Flash MX 2004提供了( 箭头工具 )工具和缩放工具来帮助用户编辑图形。

（8）根据素材的属性和作用的不同，可以将素材分为图像素材、( 视频素材 )和音频素材。

（9）根据图像显示原理的不同，图形可以分为( 位图 )和( 矢量图 )。

（10）设置帧频就是设置动画的播放速度，帧频越大，播放速度越( 快 )频越小，播放速度越( 慢 )。

（11）帧的类型有3种：( 空白帧 )、( 空白关键帧 )和关键帧。

（12）按( F6 )键可创建关键帧，按( F7 )键可创建空白关键帧，按( F5 )键可创建普通帧。

（13）图层包括普通层、( 引导 )层和( 遮照 )层。

（14）按( Ctrl+L )键可以打开“库”面板。

（15）Flash元件包括( 图形 )( 按钮 )和( 影片剪辑 )3种。

（16）如果想让一个图形元件从可见到不可见，应将其( Alpha )从( 100% )调节到0%。

（17）Flash动画分为( 逐帧动画 )和补间动画，其中补间动画又分为( 形变 )动画和( 移动 )动画。

二、选择题（1）在使用钢笔工具绘图时要将笔尖的运动轨迹预先显示出来，应在“首选参数”对话框中选中（ A ）复选框。

A、显示钢笔预览B、显示精确光标C、显示实心点（2）选择（ C ）菜单命令，将打开“场景”面板。

《马克思主义哲学原理》辩证唯物主义部分试卷（三）一、单项选择题（每小题1分，共25分）1、学习马克思主义哲学的根本目的在于（）A．说明世界B．认识世界和改造世界C．寻找现成答案D．为我所用2、认为金、木、火、土是世界本原的观点是（）A．唯心主义B．宗教唯心主义C．庸俗唯物主义D．朴素唯物主义3、哲学为具体科学的研究提供（）A．一般方法B．经验材料C．理论结论D．具体方法4、世界最古老的三大哲学传统是（）A．中国哲学、希腊哲学、印度哲学B．中国哲学、埃及哲学、德国哲学C．中国哲学、英国哲学、法国哲学D．中国哲学、俄国哲学、日本哲学5、事物的发展是上升的运动，这是由（）A．主要矛盾决定的B．基本矛盾决定的C．辩证否定的本性决定的D．矛盾的主要方面决定的6、唯物辩证法的根本方法是（）A．观察实验的方法B．逻辑推理的方法C．矛盾分析的方法D．归纳和演绎的方法7、区分量变和质变的根本标志是事物的变化（）A．速度的快慢B．状态的显著与否C．范围大小D．是否超出度的范围8、一个完整的认识过程是（）A．感性认识——理性认识——感性认识B．实践——认识——实践C．感觉——知觉——表象D．概念——判断——推理9、属于唯理论的哲学派别（）A．只有唯心主义的B．只有唯物主义的C．既可是唯心主义的也可是唯物主义的D．二元论的10、从唯物辩证法普遍联系的观点看，事物间差别的界限（）A．是完全不确定B．是确定不变的C．是难以捉摸的D．既是确定的，又是不确定的11、客观真理和唯物主义反映论，是（）A．毫无联系B．辩证统一C．不完全一致D．完全一致的12、下列哪些说法揭示了因果关系（）A．天才出于勤奋B．闪电雷鸣C．日出东方，日落西方D．冬去春来13、积劳成疾说明的哲学道理是（）A．肯定和否定B．量变引起质变C．爆旋式上升D．同一性和斗争性14、在唯物辩证法看来，水果同苹果、梨、香蕉等的关系是（）A．本质和现象关系B．内容和形式关系C．普遍性和特殊性关系D．整体和部分关系15、问题“只见树木，不见森林”是（）A．唯物辩证法的观点B．客观唯心主义观点C．形而上学观点D．不可知论观点16、世界统一于存在的观点是（）A．形而上学B．折衷主义C．唯心主义D．唯物主义17、“水中捞月”是（）A．抽象的可能性B．非现实的可能性C．现实的可能性D．不可能性18、事物由肯定、否定到否定之否定，从发展的形式上看（）A．是事物自我完善和发展的过程B．是一个不断周而复始的循环的过程C．是一个波浪式前进和螺旋式上升过程D．是一个旧事物灭亡新事物产生的过程19、物质运动最高级的形式是（）A．物理运动B．生物运动C．化学运动D．社会运动20、认识的最终目的是（）A．发现真理B．认识世界C．创立新理论D．改造世界21、主观和客观、理论和实践的统一应是（）A．循环的B．绝对的C．具体的D．无条件的22、相对主义运动观认为（）A．静止是运动的特殊状态B．运动和物质是不可分割的C．运动的形式是多样的D．只存在绝对运动而无静止23、制定我国国民经济计划的依据是（）A．现实性B．目的性C．实践性D．现实可能性24、原子衰变过程极其短促，而由猿到人的转化过程长达几百万年，这是（）A．质变过程的条件性表现B．质变过程的客观性表现C．质变形式的普遍性的表现D．质变形式的多样性的表现25、人们获得知识的根本途径是（）A．认真看书学习B．靠灵感和机遇C．靠借鉴他人经验D．积极参加社会实践二、双项选择题（每小题1分，共20分）1、一切哲学派别都不能回避，并首先要回答的问题是（）A．物质和意识的关系问题B．规律的客观性问题C．世界处于什么状态的问题D．感性认识和理性认识的关系问题E．主观和客观的关系问题2、马克思主义哲学产生的直接理论来源是（）A．黑格尔的辩证法的“合理内核”B．康德的认识论的合理内核C．费尔巴哈的唯物主义的“基本内核”D．狄德罗的唯物主义认识论E．培根、洛克的唯物主义经验论合理思想3、下列论断属于主观唯心主义的有（）A．“身外无物”B．“理在事先”C．“一念发动处便是行”D．世界是由人之外的客观精神创造的E．现实世界不过是理念的影子4、一元论（）A．是认为世界上只有一种本原的哲学学说B．指唯心主义的一元论C．指唯物主义一元论D．既有唯心主义一元论，又有唯物主义一元论E．指物质和精神都服从于一个实体——上帝5、人坐在火车上与火车一起向目的地奔驰，从运动和静止的关系上，这表明（）A．一直在运动、不存在静止B．在座位上根本没有运动C．是“动中有静”D．是“静中有动”E．运动和静止是混淆不清的6、意识的内容来自于（）A．人脑B．人的灵感C．理念D．客观世界E．实践7、片面夸大意识的能动作用会导致（）A．主观唯心主义B．客观唯心主义C．唯意志论D．形而上学唯物主义E．机械决定论8、做任何事情都要“不唯书、不唯上、只唯实”。

2024年北京第二次普通高中学业水平合格性考试英语仿真模拟试卷03考生须知1.考生要认真填写考场号和座位序号。

2.本试卷共22页，四道大题(共100分)。

3.试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

选择题必须用2B铅笔作答;非选择题必须用黑色字迹的签字笔作答。

4.考试结束后，考生应将试卷和答题卡按要求放在桌面上，待监考员收回。

一、听力理解(共25小题;每小题1分，共25分)第一节(共20小题;每小题1分，共20分)听下面十段对话或独白，从每题所给的A、B、C三个选项中，选出最佳选项，并在答题卡上将该项涂黑。

每段对话或独白你将听两遍。

听第1段材料，回答第1题。

1．What was the reason for the man to work at the charity at first?A．To help the homeless.B．To do a college project.C．To get work experience.【答案】C【原文】W:So,it says here that you did some volunteer work to raise money for a homeless charity during the summer.M:That’s right.I originally took the job because I needed some work experience for college,but helping other people really made me realize how lucky I am.听第2段材料，回答第2题。

2．Where does the conversation take place?A．On a beach.B．In a hospital.C．Over the phone.【答案】C【原文】W:San Francisco General Hospital.M:Hello.This is an emergency.Can you please send an ambulance?W:OK,OK.Just try to calm down,sir.And tell me where you are.M:Right.Uh,we are at La Traviata Restaurant in North Beach.听第3段材料，回答第3题。

人教版七年级（下）数学期末试卷（03）一、选择题（每小题3分，共30分）1．（3分）16的平方根是（）A．256B．4C．±4D．82．（3分）在平面直角坐标系中，点M（﹣2，3）在（）A．第一象限B．第二象限C．第三象限D．第四象限3．（3分）下列实数，，0.1212212221（相邻两个1之间依次多一个2），，，中，无理数有（）A．1个B．2个C．3个D．4个4．（3分）如图，直线AB，CD被EF所截，交点分别是点M，点N，则∠AMF与∠END 是（）A．同位角B．内错角C．同旁内角D．邻补角5．（3分）如果关于x的不等式3x﹣a≤﹣1的解集如图所示，则a的值是（）A．a＝﹣1B．a＝﹣2C．a≤﹣1D．a≤﹣26．（3分）如图，若AB，CD相交于点O，过点O作OE⊥AB，则下列结论不正确的是（）A．∠1与∠2互为余角B．∠3与∠2互为余角C．∠2与∠AOE互为补角D．∠AOC与∠BOD是对顶角7．（3分）如图所示，AB∥CD，若∠1＝146°，则∠2的度数是（）A．30°B．32°C．36°D．34°8．（3分）已知方程组的解也是关于x、y的二元一次方程2ax﹣3y＝0的一个解，则a的值为（）A．1.5B．2C．2.5D．39．（3分）如图，面积为7的正方形ABCD的顶点A在数轴上，且表示的数为1，若点E在数轴上，（点E在点A的右侧）且AB＝AE，则点E所表示的数为（）A．B．C．1D．+210．（3分）如图，在一个单位为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，…，是斜边在x轴上，斜边长分别为2，4，6，…的等腰直角三角形．若△A1A2A3的顶点坐标分别为A1（2，0），A2（1，﹣1），A3（0，0），则依图中所示规律，A2022的纵坐标为（）A．﹣1010B．1010C．﹣1011D．1011二、填空题（每小题3分，共24分）11．（3分）的立方根是．12．（3分）在平面直角坐标系中，若点P（﹣1，m﹣3）在x轴上，则m的值为．13．（3分）若是某个二元一次方程的一个解，则该方程可能是（请写出满足条件的一个答案即可）．14．（3分）如图，已知∠1＝∠2，则图中互相平行的线段是．15．（3分）用一组a，b，c，的值说明命题“若ac＜bc，则a＜b”是错误的，这组值可以是a＝，b＝，c＝．16．（3分）如图，AB∥CD，CE交AB于F，∠C＝54°，∠AEC＝14°，则∠A＝°．17．（3分）《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图1，图2所示，图中各行从左到右列出的算筹数分别表示未知数x，y的系数与相应的常数项．把图1表示的算筹图用我们现在所熟悉的方程组形式表述出来就是，类似地，图2所示的算筹图可以表述为．18．（3分）在平面直角坐标系xOy中，对于点P（x，y），如果点Q（x，y′）的纵坐标满足y′＝，那么称点Q为点P的“关联点”．请写出点（3，5）的“关联点”的坐标；如果点P（x，y）的关联点Q坐标为（﹣2，3），则点P 的坐标为．三、解答题（共46分，19题4分，20题5分，21题6分，22、23题每小题4分，24题6分，25题7分，26题8分）19．（4分）计算：．20．（5分）解方程组：21．（6分）求不等式组的整数解．22．（5分）如图，AB∥DC，∠B＝∠C，求证：BE∥CF．23．（5分）如图，已知点A（﹣3，3），点B（﹣4，1），点C（﹣2，2）．（1）求△ABC的面积．（2）将△ABC平移，使得点A与点D（2，4）重合，得到△DEF，点B，C的对应点分别是点E，F，画出平移后的△DEF，并写出点E和点F的坐标．24．（6分）在某官方旗舰店购买3个冰墩墩和6个雪容融毛绒玩具需1020元；购买1个冰墩墩和5个雪容融毛绒玩具需700元．（1）求冰墩墩、雪容融毛绒玩具单价各是多少元？（2）某单位准备用不超过2100元的资金在该官方旗舰店购进冰墩墩、雪容融两种毛绒玩具共20个，问最多可以购进雪容融毛绒玩具多少个？25．（7分）如图，直线AB∥CD，直线EF与AB，CD分别交于点G，H，∠EHD＝α（0°＜α＜90°）．小安将一个含30°角的直角三角板PMN按如图①放置，使点N、M分别在直线AB、CD上，且在点C、H的右侧，∠P＝90°，∠PMN＝60°．（1）填空；∠PNB+∠PMD∠P（填“＞”“＜”或“＝”）；（2）若∠MNG的平分线NO交直线CD于点O，如图②．①当NO∥EF，PM∥EF时，求α的度数；②小安将三角板PMN沿直线AB左右移动，保持PM∥EF，点N、M分别在直线AB和直线CD上移动，请直接写出∠MON的度数（用含α的式子表示）．26．（8分）在平面直角坐标系xOy中，点A，B的坐标分别为（﹣2，0），（1，0），同时将点A，B先向右平移1个单位长度，再向上平移2个单位长度，得到点A，B的对应点依次为点C，D，连接CD，AC，BD．（1）直接写出点C，D的坐标，并求出平行四边形ABDC的面积；（2）点E是坐标轴上一动点，当S△EBD＝S四边形ABDC时，请直接写出点E的坐标．附加题27．（3分）若y＝﹣+6x，则的值为．28．（3分）如图，已知AB∥CD，BE平分∠ABC，DE平分∠ADC，∠BAD＝70°，∠BCD ＝40°，则∠BED的度数为．29．（3分）m为负整数，已知二元一次方程组有整数解，则m的值为．30．（3分）关于y的不等式组的整数解是﹣3，﹣2，﹣1，0，1．则t的取值范围是．31．（8分）在平面直角坐标系中，如果点P（a，b）满足a+1＞b且b+1＞a，则称点P为“自大点”；如果一个图形的边界及其内部的所有点都不是“自大点”，则称这个图形为“自大忘形”．（1）判断下列点中，哪些点是“自大点”，直接写出点名称；P1（1，0），P2（，），P3（﹣，），P4（﹣1，﹣）（2）如果点N（2x+3，2）不是“自大点”，求出x的取值范围．（3）如图，正方形ABCD的初始位置是A（0，6），B（0，4），C（2，4），D（2，6），现在正方形开始以每秒1个单位长的速度向下（y轴负方向）平移，设运动时间为t秒（t ＞0），请直接写出当正方形成为“自大忘形”时，t的取值范围：．。

专题03 空间向量的应用一、单选题1．（2020·贵州省铜仁第一中学高二开学考试）已知两个异面直线的方向向量分别为a r ，b r ，且|a r |＝|b r|＝1，a r •12b r =-，则两直线的夹角为（ ）A ．30°B ．60°C ．120°D ．150°【答案】B【解析】设两直线的夹角为θ，则由题意可得1×1×cos a r ＜，12b =-r ＞，∴cos a r ＜，12b =-r ＞，∴a r ＜，23b p =r ＞，∴θ3p =，故选：B ．2．（2019·穆棱市第一中学高二期末）若平面,a b 的法向量分别为1,1,3,(1,2,6)2a b æö=-=--ç÷èør r ，则（ ）A ．//a bB ．a 与b 相交但不垂直C ．a b^D ．//a b 或a 与b 重合【答案】D【解析】因为12a b =-r r ，所以平面,a b 的法向量共线，故//a b 或a 与b 重合.故选：D.3．（2020·北京高二期末）已知直线l 的方向向量为m u r ,平面a 的法向量为n r ,则“0m n ×=u r r”是“l ∥a ”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】B【解析】Q 0m n ×=u r r \m n^u r r Q 0m n ×=u r r ,即m n ^u r r ,不一定有l ∥a ,也可能l aÌ\“0m n ×=u r r ”是“l ∥a ”的不充分条件Q l ∥a ,可以推出m n ^u r r ,\“0m n ×=u r r ”是“l ∥a ”是必要条件,综上所述, “0m n ×=u r r ”是“l ∥a ”必要不充分条件.故选:B.4．（2019·山东省济南一中高二期中）在平面ABCD 中，(0,1,1)A ，(1,2,1)B ，(1,0,1)C --，若(1,,)a y z =-v ，且a v 为平面ABCD 的法向量，则2y 等于（ ）A ．2B ．0C ．1D ．无意义【答案】C【解析】由题得，(1,1,0)AB =uuu r ，(1,1,2)AC =--uuu r ，又a r 为平面ABCD 的法向量，则有00a AB a AC ì×=í×=îuuu v v uuu v v ，即10120y y z -+=ìí-+=î，则1y =，那么21y =.故选：C5．（2019·四川省双流中学高三月考）已知点P 是正方体1111ABCD A B C D -的棱CD 的中点，给出以下结论：①11A P C D ^；②1A P BD ^；③11A P BC ^；④1AP ^平面1BC D 其中正确命题的序号是（ ）A ．①B ．②C ．③D ．④【答案】C【解析】设正方体边长为2,建立如图空间直角坐标系.则()12,1,2A P =--uuur .对①, ()10,2,2C D =--uuuu r ,因为110242A P C D ×=-+=uuur uuuu r ,故①错误.对②, ()2,2,0BD =--uuu r ,因为1422A P BD ×=-=uuur uuu r ,故②错误.对③, ()12,0,2BC =-uuuu r ,因为1440A P BD ×=-=uuur uuu r ,故③正确.对④,由②有1A P BD ^不成立,故1AP ^平面1BC D 不成立.故④错误.故选：C6．（2019·穆棱市第一中学高二期末）如图，在正方体ABCD ­1111A B C D 中，以D 为原点建立空间直角坐标系，E 为B 1B 的中点，F 为11A D 的中点，则下列向量中，能作为平面AEF 的法向量的是( )A ．(1，－2，4)B ．(－4,1，－2)C ．(2，－2，1)D ．(1，2，－2)【答案】B【解析】设正方体棱长为2，则A （2，0，0），E （2，2，1），F （1，0，2），∴AE uuu r =（0，2，1），AF uuu r =（﹣1，0，2）设向量n r=（x ，y ，z ）是平面AEF 的一个法向量则2020n AE y z n AF x z ì×=+=ïí×=-+=ïîuuu r r uuu r r ，取y=1，得x=﹣4，z=﹣2∴n r =（﹣4，1，﹣2）是平面AEF 的一个法向量因此可得：只有B 选项的向量是平面AEF 的法向量故选：B ．7．（2019·包头市第四中学高二期中）在棱长为2的正方体1111ABCD A B C D -中，E ，F 分别为棱1AA 、1BB 的中点，M 为棱11A B 上的一点，且1(02)A M l l =<<，设点N 为ME 的中点，则点N 到平面1D EF 的距离为（ ）ABCD【答案】D【解析】以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系，则M （2，λ，2），D 1（0，0，2），E （2，0，1），F （2，2，1），1ED uuuu v ＝（﹣2，0，1），EF uuu r ＝（0，2，0），EM uuuu r ＝（0，λ，1），设平面D 1EF 的法向量n r＝（x ，y ，z ），则1·20·20n ED x z n EF y ì=-+=í==îuuuu v v uuuv v ，取x ＝1，得n r ＝（1，0，2），∴点M 到平面D 1EF=N 为EM 中点，所以N ，选D ．8．（2020·湖南省高二期末）已知直三棱柱111ABC A B C -中，底面边长和侧棱长都相等，则异面直线1AB 与1BC 所成的角的余弦值为（ ）A ．12B ．18C ．14D ．34【答案】C【解析】立空间坐标系如图，设边长为2，得到A （2，0，0），1B （12），B （10），1C （0，0，2）向量()()112,­1,2AB BC =-=uuuv uuuu v 设异面直线夹角为q ，则1111cos =||||AB BC AB BC q ×=×uuuv uuuu v uuuv uuuu v 14故答案为C9．（2018·山西省山西大附中高二期中）过正方形ABCD 的顶点A ，作PA ^平面ABCD ，若PA BA =，则平面ABP 和平面CDP 所成的锐二面角的大小是A ．30°B ．45°C ．60°D ．90°【答案】B【解析】法一：建立如图(1)所示的空间直角坐标系，不难求出平面APB 与平面PCD 的法向量分别为n 1＝(0,1,0)，n 2＝(0,1,1)，故平面ABP 与平面CDP 所成二面角的余弦值为1212n n n n＝，故所求的二面角的大小是45°.法二：将其补成正方体．如图(2)，不难发现平面ABP 和平面CDP 所成的二面角就是平面ABQP 和平面CDPQ 所成的二面角，其大小为45°.10．（2020·山东省章丘四中高二月考）在正方形1111ABCD A B C D -中，棱AB ，11A D 的中点分别为E ，F ，则直线EF 与平面11AA D D 所成角的余弦值为（ ）A B C D 【答案】D【解析】以D 为原点，DA 为x 轴，DC 为y 轴，1DD 为z 轴，建立空间直角坐标系，设正方体1111ABCD A B C D -的棱长为2，则()2,1,0E ， ()1,0,2F ， ()1,1,2EF =--uuu r ，平面11AA D D 的法向量()0,1,0n =r ，设直线EF 与平面11AA D D 所成角为q ，0,2p éùqÎêúëû，则||sin ||||EF n EF n q ===uuu r r g uuu r r g ．所以cos q ==\直线EF 与平面11AA D D 故选：D ．二、多选题11．（2020·山东省高二期末）已知ν为直线l 的方向向量，1n ,2n 分别为平面α，β的法向量（α，β不重合），那么下列选项中，正确的是（ ）A ．12////n n a bÛB ．12n n a b^Û^C ．1////n l n aÛD ．1//n l n a ^Û【答案】AB【解析】A 选项，平面α，β不重合，所以平面α，β的法向量平行等价于平面α，β平行，正确；B 选项，平面α，β不重合，所以平面α，β的法向量垂直等价于平面α，β垂直，正确；C 选项，直线的方向向量平行于平面的法向量等价于直线垂直于平面，错误；D 选项，直线的方向向量垂直于平面的法向量等价于直线平行于平面或直线在平面内，错误.故选：AB12．（2019·山东省高三）正方体1111ABCD A B C D -的棱长为1，,,E F G 分别为11,,BC CC BB 的中点．则（ ）A ．直线1D D 与直线AF 垂直B ．直线1A G 与平面AEF 平行C ．平面AEF 截正方体所得的截面面积为98D ．点C 和点G 到平面AEF 的距离相等【答案】BC【解析】对选项A ：（方法一）以D 点为坐标原点，DA 、DC 、1DD 所在的直线分别为x 、y 、z 轴，建立空间直角坐标系，则(0,0,0)D 、(1,0,0)A 、1(1,0,1)A 、1,1,02E æöç÷èø、10,1,2F æöç÷èø、11,1,2G æöç÷èø.从而1(0,0,1)DD =uuuu r ，11,1,2AF æö=-ç÷èø，从而1102DD AF ×=¹uuuu r uuu r ，所以1DD 与直线AF 不垂直，选项A 错误；（方法二）取1DD 的中点N ，连接AN ，则AN 为直线AF 在平面11ADD A 内的射影，AN 与1DD 不垂直，从而AF 与1DD 也不垂直，选项A 错误；取BC 的中点为M ，连接1A M 、GM ，则1A M AE ∥，GM EF ∥，易证1A MG AEF 平面∥平面，从而1A G AEF ∥平面，选项B 正确；对于选项C ，连接1AD ，1D F ，易知四边形1AEFD 为平面，且1D H AH ==，1A D =132AD H S D ==，而113948AD H AEFD S S ==四边形△，从而选项C 正确；对于选项D ：（方法一）由于111111112222224GEF EBG BEFG S S S D D æö=-=+´-´´=ç÷èø梯形，而11112228ECF S D =´´=，而13A GEF EFG V S AB -D =×，13A ECF ECF V S AB -D =×，所以2A GEF A ECF V V --=，即2G AEFC AEF V V --=，点G 到平面AEF 的距离为点C 到平面AEF 的距离的二倍.从而D 错误.（方法二）假设点C 与点G 到平面AEF 的距离相等，即平面AEF 将CG 平分，则平面AEF 必过CG 的中点，连接CG交EF于点O ，易知O 不是CG 的中点，故假设不成立，从而选项D 错误.13．（2020·福建省高二期末）正方体1111ABCD A B C D -中，E 、F 、G 、H 分别为1CC 、BC 、CD 、BB 、1BB 的中点，则下列结论正确的是（ ）A ．1B G BC^B ．平面AEF I 平面111AA D D AD =C ．1//A H 面AEFD ．二面角E AF C --的大小为4p 【答案】BC【解析】由题可知，1B G 在底面上的射影为BG ，而BC 不垂直BG ，则1B G 不垂直于BC ，则选项A 不正确；连接1AD 和1BC ，E 、F 、G 、H 分别为1CC 、BC 、CD 、BB 、1BB 的中点，可知11////EF BC AD ，所以AEF D Ì平面1AD EF ，则平面AEF I 平面111AA D D AD =，所以选项B 正确；由题知，可设正方体的棱长为2，以D 为原点，DA 为x 轴，DC 为y 轴，1DD 为z 轴，则各点坐标如下：()()()()()()12,0,0,0,2,0,0,2,1,2,0,2,2,2,1,1,2,0A C E A H F ()()()()110,2,1,1,2,0,1,0,1,0,0,2A H AF EF AA =-=-=-=uuuu r uuu r uuu r uuur ，设平面AEF 的法向量为(),,n x y z =r ，则00n AF n EF ì×=í×=îuuu v v uuu v v ，即200x y x z -+=ìí-=î，令1y =，得2,2x z ==，得平面AEF 的法向量为()2,1,2n =r ，所以10A H n ×=uuuu r r ，所以1//A H 平面AEF ，则C选项正确；由图可知，1AA ^平面AFC ，所以1AA uuur是平面AFC 的法向量，则1112cos ,3AA n AA n AA n×<>===×uuur r uuur r uuur r .得知二面角E AF C --的大小不是4p ，所以D 不正确.故选：BC.三、填空题14．（2019·山东省济南一中高二期中）若平面a的一个法向量为(n =v，直线l的一个方向向量为a =v ，则l 与a 所成角的正弦值为________.【答案】15【解析】由题，设l 与a 所成角为q，可得||1sin 5||||n a n a q ×===v v v v .故答案为：1515．（2019·陕西省西北大学附中高二期中）如图，在正三棱柱111ABC A B C -中，12,AB AC AA === ,E F 分别是,BA11A C 的中点.设D 是线段11B C 上的（包括两个端点）动点，当直线BD 与EF，则线段BD 的长为_______．【答案】【解析】以E 为原点，EA,EC 为x,y轴建立空间直角坐标系，如下图．1(0,0,0),,2),(0,1,0),(0,,2)(11)2E F B D t t --££1,2),(0,1,2)2EF BD t ==+uuu v uuuv cos q =解得t=1，所以BD =，填．点睛：利用空间向量求解空间角与距离的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.16．（2019·浙江省宁波市鄞州中学高二期中）正方体1111ABCD A B C D -中，,E F 分别是1,AA AB 的中点，则EF 与直线1AC 所成角的大小为______ ；EF 与对角面11BDD B 所成角的正弦值是 __________．【答案】2p 12【解析】如图所示建立空间直角坐标系，设正方体的边长为2，则()2,0,1E ，()2,1,0F ，()2,0,0A ，()10,2,2C ，故()0,1,1EF =-uuu r ，()12,2,2AC =-uuuu r .故10EF AC ×=uuu r uuuu r ，故EF 与直线1AC 所成角的大小为2p .易知对角面11BDD B 的一个法向量为()1,1,0n =-r ，设EF 与对角面11BDD B 所成角为q ，故1sin cos ,2EF n EF n EF n q ×===×uuu r r uuu r r uuu r r .故答案为：2p ；12.17．（2019·江西省会昌中学高二月考）已知正方体1111ABCD A B C D -的棱长为a ，点E ，F ，G 分别为棱A B ，1AA ，11C D 的中点，下列结论中，正确结论的序号是___________.①过E ，F ，G 三点作正方体的截面，所得截面为正六边形；②11//B D 平面EFG ；③1BD ^平面1ACB ；④异面直线EF 与1BD ；⑤四面体11ACB D 的体积等于312a .【答案】①③④【解析】延长EF 分别与1l B A ，1B B 的延长线交于N ，Q ，连接GN 交11A D 于H ，设HG 与11B C 的延长线交于P ，连接P Q 交1CC 于I ，交BC 于M ，连FH ，HG ，GI ，IM ，ME ,EF ,如图:则截面六边形EFHGIM 为正六边形，故①正确：因为11B D 与HG 相交，故11B D 与平面EFG 相交，所以②不正确：1,BD AC BD AC ^\^Q (三垂线定理)，1111,BC B C BD B C ^\^Q (三垂线定理)，且AC 与1B C 相交，所以1BD ^平面1ACB ，故③正确；以D 为原点,1,,DA DC DD 分别为,,x y z 轴建立空间直角坐标系,则1(0,0,0),(,,0),(,0,),(,,0),(0,0,)22a a D E a F a B a a D a ,则(0,,)22a a EF =-uuu r ,1(,,)BD a a a =--uuuu r ,所以111cos ,||||EF BD EF BD EF BD ×<>=uuu r uuuu r uuu r uuuu r uuu r uuuur ===所以1sin ,EF BD <>==uuu r uuuu r=所以111sin ,tan ,cos ,EF BD EF BD EF BD <><>=<>uuu r uuuu r uuu r uuuu r uuu r uuuur ==,所以异面直线EF 与1BD，故④正确；因为四面体11ACB D 的体积等于正方体的体积减去四个正三棱锥的体积，即为3331114323a a a -´´=，故⑤不正确．故答案为：①③④四、解答题18．（2019·广西壮族自治区田东中学高二期中）已知三棱柱111ABC A B C -的侧棱垂直于底面，90BAC Ð=°，12AB AA ==，1AC =，M ，N 分别是11A B ，BC 的中点．（1）求证：1AB AC ^；（2）求证：//MN 平面11ACC A .【答案】(1)证明见解析 (2) 证明见解析【解析】Q 三棱柱为直三棱柱 1AA \^平面ABC 1AA AC \^，1AA AB ^又90BAC Ð=o ，则1,,AB AC AA 两两互相垂直，可建立如下图所示的空间直角坐标系则()0,0,0A ，()0,2,0B ，()1,0,0C -，()11,0,2C -，()0,1,2M ，1,1,02N æö-ç÷èø（1）()0,2,0AB =uuu r Q ，()11,0,2AC =-uuuu r ()10120020AB AC \×=´-+´+´=uuu r uuuu r 1AB AC \^（2）由题意知：AB uuu r是平面11ACC A 的一个法向量()0,2,0AB =uuu r Q ，1,0,22MN æö=--ç÷èøuuuu r ()10200202AB MN æö\×=´-+´+´-=ç÷èøuuu r uuuu r AB MN \^uuu r uuuu r MN ËQ 平面11ACC A //MN \平面11ACC A 19．（2020·陕西省高二期末）如图，在棱长为2的正方体1111ABCD A B C D -中E ，F 分别为AB ，1A C的中点.（1）求EF ；（2）求证：//EF 平面11AA D D【答案】（1；（2）证明见解析【解析】（1）由题知,(2,1,0)E ,(1,1,1)F ,∴(1,0,1)EF =-uuu r ,∴||EF ==uuu r （2）由题知,(2,0,0)A ,1(0,0,2)D ,∴1(2,0,2)AD =-uuuu r ,∴12AD EF =uuuu r uuu r ,故//AD EF ,又1AD Ì平面11AA D D ,EF Ë平面11AA D D∴EF ∥平面11AA D D .20.（2020·北京高二期末）如图，在直三棱柱111ABC A B C -中，3AC =，4BC =，5AB =，14AA =，点D 是AB 的中点．（1）求异面直线AC 与1BC 所成的角；（2）求证：1//AC 平面1CDB ．【答案】（1）2p （2）证明见解析【解析】（1）因为3AC =，4BC =，5AB =，所以222AC BC AB +=，所以ABC D 是直角三角形，所以2ACB p=，所以AC BC^因为三棱柱111ABC A B C -为直三棱柱，所以1C C ^平面ABC ，所以1C C AC ^，1C C BC^以C 为原点，分别以CA 、CB 、1CC 为x 轴、y 轴、z 轴，建立空间直角坐标系，则(0C ，0，0)，(3A ，0，0)，(0B ，4，0)，1(0C ，0，4)所以直线AC 的方向向量为(3,0,0)CA =uuu r ，直线1BC 的方向向量为1(0,4,4)BC =-uuuu r ，设异面直线AC 与1BC 所成的角为q ，因为10CA BC =uuu r uuuu r g ，所以cos 0q =，所以异面直线AC 与1BC 所成的角为2p．（2）由（1）可知3,2,02D æöç÷èø，1(0B ，4，4)，则3,2,02CD æö=ç÷èøuuu r ，1(0,4,4)CB =uuur 设平面1CDB 的法向量为(,,)n x y z =r ，则1·0·0CD n CB n ì=ïí=ïîuuu v v uuuv v ，所以3202440x y y z ì+=ïíï+=î令4x =，则3y =-，3z =，所以(4,3,3)n =-r直线1AC 的方向向量为1(3,0,4)AC =-uuuu r ，因为10AC n =uuuu r r g ，1AC Ë平面1CDB ， 所以1//AC 平面1CDB ．21．（2020·银川三沙源上游学校高二期末）如图，在直三棱柱111ABC A B C -中，AB AC ^，2AB AC ==，1AA =，D 为棱BC 的中点.（1）求直线1DB 与平面11AA C C 所成角的正弦值；（2）求平面11AA C C 与平面1ADB 所成二面角的余弦值.【答案】（12）.【解析】则(0,0,0)A ，1(0,0,A ，(2,0,0)C ，(0,2,0)B ，(1,1,0)D ，1(0,2,B ，所以(2,0,0)AC =uuu r ，1(0,0,AA =uuur ，(1,1,0)AD =uuu r ，1(1,1,DB =-uuuu r ，如下图：（1）设平面11AA C C 的一个法向量为(,,)m x y z =u r ，则100AC m AA m ì×=ïí×=ïîuuu v v uuuv v，即00ìïí=ïî，取(0,1,0)m =u r ，所以1cos ,DB m <=uuuu r u r ，所以直线1DB 与平面11AA C C（2）设平面1ADB 的一个法向量为111(,,)n x y z =r ，则100AD n DB n ì×=ïí×=ïîuuu v v uuuu v v，即1111100x y x y +=ìïí-++=ïî，取(1,n =-r ，所以cos ,m n <=u r r ，所以求平面11AA C C 与平面1ADB所成二面角的余弦值.22．（2019·江苏省苏州实验中学高一月考）直四棱柱1111ABCD A B C D -中，2AB BC ==，90ABC Ð=°，E 、F 分别为棱AB 、11B C 上的点，2AE EB =，112C F FB =.求证：（1）//EF 平面11AA C C ；（2）线段AC 上是否存在一点G ，使面EFG ^面11AA C C .若存在，求出AG 的长；若不存在，请说明理由.【答案】（1）证明见解析（2）存在，AG =【解析】（1）如图所示：以1A 为原点，11A D ，11A B ，1A A 分别为,,x y z 轴建立空间直角坐标系：则1(0,0,0)A ，1(0,2,0)B ，1(2,2,0)C ，设(0,0,)A a ，则4(0,,)3E a ，2(,2,0)3F ，所以22(,,)33EF a =-uuu r ，1(0,0,)A A a =uuur ，11(2,2,0)AC =uuuu r ，因为11113EF A A A C =-+uuu r uuur uuuu r ，所以EF uuu r ，1A A uuur ，11AC uuuu r 共面，又EF 不在平面11AA C C 内，所以//EF 平面11AA C C（2）线段AC 上存在一点G ，使面EFG ^面11AA C C ，且AG =证明如下：在三角形AGE 中，由余弦定理得EG ====，所以222AG EG AE +=，即EG AG ^，又1A A ^平面ABCD ，EG Ì平面ABCD ，所以1A A EG ^，而1AG A A A Ç=，所以EG ^平面11AA C C ，因为EG Ì平面EFG ，所以EFG ^面11AA C C .23．（2020·北京高二期末）如图，在底面是正方形的四棱锥P ABCD -中，PA ^平面ABCD ，2AP AB ==，,,E F G 是,,BC PC CD 的中点.（1）求证：BG ^平面PAE ；（2）在线段BG 上是否存在点H ，使得//FH 平面PAE ？若存在，求出BH BG 的值；若不存在，说明理由.【答案】（1）证明见解析；（2）存在，35.【解析】（1）证明：因为四棱锥P ABCD -底面是正方形，且PA ^平面ABCD ，以点A 为坐标原点，,,AB AD AP所在直线分别为,,x y z 轴建立如图所示空间直角坐标系.则(0,0,0),(2,0,0),(0,0,2),A B P ，(2,2,0),(0,2,0)C D ，因为,,E F G 是,,BC PC CD 的中点，所以(2,1,0),(1,1,1),(1,2,0)E F G ，所以(1,2,0)BG =-uuu v ，(0,0,2),(2,1,0),AP AE ==uuu v uuu v 所以0BG AP ×=uuu v uuu v ，且0BG AE ×=uuu v uuu v . 所以BG AP ^，BG AE ^，且AE AP A =I .所以BG ⊥平面PAE .（2）假设在线段BG 上存在点H ，使得FH //平面PAE . 设BH BG l =uuuv uuu v (01)l ££，则(1,21,1)FH FB BH AB AF BG l l l =+=-+=---uuuv uuu v uuuv uuu v uuu v uuu v .因为FH //平面PAE ，BG ⊥平面PAE ，所以(1)(12(21)0(1)530FH GB l l l ×=-×-+-+´-=-=uuuv uuu v . 所以35l =. 所以，在线段BG 上存在点H ，使得FH //平面PAE .其中35BH BG =.。