江苏省南京航空航天大学附属高级中学2020-2021学年高二上学期数学周测试卷(一)(扫描版,无答案)

2020-2021学年江苏省南京市玄武区人民中学高二（上）月考数学试卷（9月份）一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的，请把答案填涂在答题卡相应位置上.1．（5分）计算sin43°cos13°﹣cos43°sin13°的结果等于（）A．B．C．D．2．（5分）已知△ABC中，角A，B，C所对的边分别是a，b，c，且，则sin B＝（）A．B．C．D．3．（5分）若方程x2+y2﹣4x+2y+5k＝0表示圆，则实数k的取值范围是（）A．（﹣∞，1）B．（﹣∞，1]C．[1，+∞）D．R4．（5分）圆柱的侧面展开图是一个边长为2的正方形，那么这个圆柱的体积是（）A．B．C．D．5．（5分）已知M（﹣3，0），N（3，0），|PM|﹣|PN|＝6，则动点P的轨迹是（）A．一条射线B．双曲线右支C．双曲线D．双曲线左支6．（5分）设抛物线y2＝12x的焦点为F，点P在此抛物线上且横坐标为5，则|PF|等于（）A．4B．6C．8D．107．（5分）下列三图中的多边形均为正多边形，M，N是所在边的中点，双曲线均以图中的F1，F2为焦点，设图示①②③中的双曲线的离心率分别为e1，e2，e3、则e1，e2，e3的大小关系为（）A．e1＞e2＞e3B．e1＜e2＜e3C．e2＝e3＜e1D．e1＝e3＞e2 8．（5分）某同学数星星的时候，突然想到了哈雷彗星：信息技术老师给他找了一幅哈雷慧星图片和轨道图片，地理老师告诉他哈雷慧星近日点距离太阳约0.6A．U．，将于2023年12月9日出现的远日点距离太阳约35A．U．（A．U．是天文单位，天文学中计量天体之间距离的一种单位，其数值取地球和太阳之间的平均距离，1A．U．＝149，597，870千米）物理老师告诉他该彗星的周期约76年，质量约1015kg．化学老师说：彗核的成分以水冰为主，占70%，它只是个很松散的大雪堆而已，数学老师问：哈雷慧星的轨迹可以近似看成椭圆，那么该椭圆的离心率约是多少呢？（）A．1.03B．0.97C．0.83D．0.77二、多项选择题：本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求，请把答案填涂在答题卡相应位置上，全部选对得5分，部分选对得3分，不选或有错选的得0分9．（5分）以下命题（其中a，b表示直线，α表示平面），其中错误的是（）A．若a∥b，b⊂α，则a∥αB．若a∥α，b∥α，则a∥bC．若a∥b，b∥α，则a∥αD．若a∥α，a⊂β，α∩β＝b，则a∥b10．（5分）关于双曲线C1：＝1与双曲线C2：＝﹣1，下列说法正确的是（）A．它们有相同的渐近线B．它们有相同的顶点C．它们的离心率不相等D．它们的焦距相等11．（5分）已知方程mx2+ny2＝1，其中m2+n2≠0，则（）A．mn＞0时，方程表示椭圆B．mn＜0时，方程表示双曲线C．n＝0时，方程表示抛物线D．n＞m＞0时，方程表示焦点在x轴上的椭圆12．（5分）如图A（2，0），B（1，1），C（﹣1，1），D（﹣2，0），是以OD为直径的圆上一段圆弧，是以BC为直径的圆上一段圆弧，是以OA为直径的圆上一段圆弧，三段弧构成曲线Ω．则下面说法正确的是（）A．曲线Ω与x轴围成的面积等于B．与的公切线方程为：C．所在圆与所在圆的交点弦方程为：x﹣y＝0D．用直线y＝x截所在的圆，所得的弦长为三、填空题：本题共4小题，每小题5分，共20分.请把答案填写在答题卡相应位置上13．（5分）抛物线y＝4x2的准线方程为．14．（5分）双曲线﹣＝1的焦点到其渐近线的距离为．15．（5分）已知点A（﹣2，1），y2＝﹣4x的焦点是F，P是y2＝﹣4x上的点，为使|P A|+|PF|取得最小值，P点的坐标是．16．（5分）如图，AB为圆O的直径，点C在圆周上（异于点A，B），直线P A垂直于圆O 所在的平面，点M是线段PB的中点．有以下四个命题：①MO∥平面P AC；②P A∥平面MOB；③OC⊥平面P AC；④平面P AC⊥平面PBC．其中正确的命题的序号是．四、解答题：本大题共6小题，共70分.请在答题卡指定区域内作答，解答时应写出必要的文字说明，证明过程或演算步骤.17．（10分）已知函数f（x）＝x．（1）求函数f（x）的值域；（2）求函数f（x）单调递增区间．18．（12分）已知直线l1：x+2ay+1＝0，直线l2：（3a﹣1）x﹣ay﹣7＝0．（1）若l1⊥l2，求实数a的值；（2）若l1∥l2，求实数a的值．19．（12分）如图，四棱锥P﹣ABCD的底面是边长为2的菱形，PD⊥底面ABCD．（1）求证：AC⊥平面PBD；（2）若PD＝2，直线PB与平面ABCD所成的角为45°，求四棱锥P﹣ABCD的体积．20．（12分）已知抛物线y2＝2px（p＞0）的准线方程为x＝﹣1．（Ⅰ）求p的值；（Ⅱ）直线l：y＝x﹣1交抛物线于A、B两点，求弦长|AB|．21．（12分）已知点P（﹣2，1）在椭圆C：+＝1（a＞0）上，动点A，B都在椭圆上，且直线AB不经过原点O，直线OP经过弦AB的中点．（1）求椭圆C的方程和直线AB的斜率；（2）求△P AB面积的最大值．22．（12分）已知离心率为的椭圆E：+＝1（a＞b＞0）经过点A（1，）．（1）求椭圆E的方程；（2）若不过点A的直线l：y＝x+m交椭圆E于B，C两点，求△ABC面积的最大值．参考答案与试题解析一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的，请把答案填涂在答题卡相应位置上.1．【分析】观察所求的式子发现满足两角和与差的正弦函数公式sinαcosβ﹣cosαsinβ＝sin（α﹣β），故利用此公式及特殊角的三角函数值化简即可求出原式的值．【解答】解：sin43°cos13°﹣cos43°sin13°＝sin（43°﹣13°）＝sin30°＝．故选：A．2．【分析】由已知利用正弦定理即可求解sin B的值．【解答】解：因为，由正弦定理，可得．故选：A．3．【分析】由方程x2+y2﹣4x+2y+5k＝0配方可得（x﹣2）2+（y+1）2＝5﹣5k，此方程表示圆，则5﹣5k＞0，解得即可．【解答】解：由方程x2+y2﹣4x+2y+5k＝0可得（x﹣2）2+（y+1）2＝5﹣5k，此方程表示圆，则5﹣5k＞0，解得k＜1．故实数k的取值范围是（﹣∞，1）．故选：A．4．【分析】由题意求出圆柱的高和底面圆半径，再求圆柱的体积．【解答】解：如图所示，圆柱的侧面展开图是一个边长为2的正方形，则圆柱的高为h＝2，底面圆的周长为2πr＝2，解得r＝，∴圆柱的体积是V＝πr2h＝π••2＝．故选：A．5．【分析】先计算|MN|，从而有|PM|﹣|PN|＝|MN|，故可确定点P的轨迹．【解答】解：由题意，|MN|＝3+3＝6，∵|PM|﹣|PN|＝6，∴|PM|﹣|PN|＝|MN|，∴点P的轨迹是射线．故选：A．6．【分析】利用抛物线的标准方程，求出p，通过定义转化求解即可．【解答】解：抛物线y2＝12x的焦点在x轴上，P＝6，由抛物线的定义可得：．故选：C．7．【分析】根据题设条件，分别建立恰当的平面直角坐标系，求出图示①②③中的双曲线的离心率e1，e2，e3，然后再判断e1，e2，e3的大小关系．【解答】解：①设等边三角形的边长为2，以底边为x轴，以底边的垂直平分线为y轴，建立平面直角坐标系，则双曲线的焦点为（±1，0），且过点（，），∵（，）到两个焦点（﹣1，0），（1，0）的距离分别是和，∴，c＝1，∴．②正方形的边长为，分别以两条对角线为x轴和y轴，建立平面直角坐标系，则双曲线的焦点坐标为（﹣1，0）和（1，0），且过点（）．∵点（）到两个焦点（﹣1，0），（1，0）的距离分别是和，∴，c＝1，∴．③设正六边形的边长为2，以F1F1所在直线为x轴，以F1F1的垂直平分线为y轴，建立平面直角坐标系，则双曲线的焦点为（﹣2，0）和（2，0），且过点（1，），∵点（1，）到两个焦点（﹣2，0）和（2，0）的距离分别为2和2，∴a＝﹣1，c＝2，∴．所以e1＝e3＞e2．故选：D．8．【分析】设椭圆的长半轴长为a，半焦距为c，由题意列方程求得a与c的值，则离心率可求．【解答】解：设椭圆的长半轴长为a，半焦距为c，由题意可得，解得a＝17.8，c＝17.2，∴e＝．故选：B．二、多项选择题：本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求，请把答案填涂在答题卡相应位置上，全部选对得5分，部分选对得3分，不选或有错选的得0分9．【分析】对于A，a∥α或a⊂α；对于B，a与b相交、平行或异面；对于C，a∥α或a⊂α；对于D，由线面平行的性质得a∥b．【解答】解：由a，b表示直线，α表示平面，知：对于A，若a∥b，b⊂α，则a∥α或a⊂α，故A错误；对于B，若a∥α，b∥α，则a与b相交、平行或异面，故B错误；对于C，若a∥b，b∥α，则a∥α或a⊂α，故C错误；对于D，若a∥α，a⊂β，α∩β＝b，则由线面平行的性质得a∥b，故D正确．故选：ABC．10．【分析】求解两个双曲线的顶点坐标，渐近线方程，离心率，焦距判断选项即可．【解答】解：双曲线C1：＝1的顶点坐标（±3，0），渐近线方程：4x±3y＝0，离心率为：，焦距为10．双曲线C2：＝﹣1，即：，它的顶点坐标（±4，0），渐近线方程：3x±4y＝0，离心率为：，焦距为10．所以它们的离心率不相等，它们的焦距相等．故选：CD．11．【分析】由椭圆方程和双曲线方程、抛物线方程的特点，可判断结论．【解答】解：方程mx2+ny2＝1，其中m2+n2≠0，当m＜0，n＜0时，方程不表示椭圆，故A错；当mn＜0时，方程表示双曲线，故B对；当n＝0时，mx2＝1，m＞0，方程表示两条直线；m≤0时，不表示任何图象，故C错；n＞m＞0时，方程表示焦点在x轴上的椭圆，故D对．故选：BD．12．【分析】首先利用分割法的应用求出曲线Ω与x轴围成的曲变形的面积，进一步利用点到直线的距离和直线的平行的应用求出圆的公切线的方程，最后利用垂径定理的应用和勾股定理的应用求出结果．【解答】解：根据题意：圆弧AB表示为以（1，0）为圆心，1为半径的圆的周长的．圆弧BC表示为以（0，1）为圆心，1为半径的圆的周长的．圆弧CD是以（﹣1，0）为圆心，1为半径的圆的周长的．所以把图形进行分割，如图所示：①所以曲线Ω与x轴围成的图形的面积为S＝，故选项A错误．②由于圆弧AB表示为以（1，0）为圆心，1为半径的圆．圆弧BC表示为以（0，1）为圆心，1为半径的圆．所以和所在的圆的公切线平行于经过（1，0）和（0，1）的直线，所以设直线的斜率k＝﹣1，设直线的方程为x+y+b＝0，所以（0，1）到直线x+y+b＝0的距离d＝，解得b＝或，根据图象得：公切线的方程为x+y﹣，故选项B正确．③以和所在的圆的方程为（x﹣1）2+y2＝1.所在的圆的方程为x2+（y﹣1）2＝1，两圆相减得：x﹣y＝0．④所在的圆的方程为（x+1）2+y2＝1，所以圆心（﹣1，0）到直线x﹣y＝0的距离d＝，所以所截的弦长为l＝2，故选项D错误．故选：BC．三、填空题：本题共4小题，每小题5分，共20分.请把答案填写在答题卡相应位置上13．【分析】先把抛物线方程整理成标准方程，进而求得p，再根据抛物线性质得出准线方程．【解答】解：整理抛物线方程得x2＝y，∴p＝∵抛物线方程开口向上，∴准线方程是y＝﹣故答案为：．14．【分析】先由题中条件求出焦点坐标和渐近线方程，再代入点到直线的距离公式即可求出结论．【解答】解：由题得：其焦点坐标为（﹣，0），（，0）．渐近线方程为y＝±x，即x﹣2y＝0，所以焦点到其渐近线的距离d＝＝．故答案为：．15．【分析】过P作PK⊥l（l为抛物线的准线）于K，则|PF|＝|PK|，进而问题转化为求|P A|+|PK|的最小值，当P，A，K三点共线时即当P点的纵坐标与A点的纵坐标相同时，|P A|+|PK|最小，把y＝1代入抛物线方程求得x，则点P的纵坐标可得，进而求得P的坐标．【解答】解：过P作PK⊥l（l为抛物线的准线）于K，则|PF|＝|PK|，∴|P A|+|PF|＝|P A|+|PK|．∴当P点的纵坐标与A点的纵坐标相同时，|P A|+|PK|最小，此时P点的纵坐标为1，把y＝1代入y2＝﹣4x，得x＝﹣，即当P点的坐标为（﹣，1）时，|P A|+|PF|最小．故答案为：．16．【分析】①先证明MO∥P A，即可判定MO∥平面P AC；②P A在平面MOB内，可得②错误；③可证P A⊥BC，BC⊥平面P AC．即可证明OC⊥平面P AC不成立；④由③知BC⊥平面P AC，即可证明平面P AC⊥平面PBC．【解答】解：①因为MO∥P A，MO⊄平面P AC，P A⊂平面P AC，所以MO∥平面P AC；②因为P A在平面MOB内，所以②错误；③因为P A垂直于圆O所在的平面，所以P A⊥BC．又BC⊥AC，AC∩P A＝A，所以BC⊥平面P AC．因为空间内过一点作已知平面的垂线有且只有一条，所以OC⊥平面P AC不成立，③错误；④由③知BC⊥平面P AC，且BC⊂平面PBC，所以平面P AC⊥平面PBC．正确命题的序号是①④．故答案为：①④．四、解答题：本大题共6小题，共70分.请在答题卡指定区域内作答，解答时应写出必要的文字说明，证明过程或演算步骤.17．【分析】（1）利用辅助角公式进行化简，结合三角函数的有界性进行求解即可．（2）根据三角函数的单调性的性质进行求解即可．【解答】解：（1）f（x）＝x＝sin2x+1+cos2x＝2sin（2x+）+1，∵﹣1≤sin（2x+）≤1，∴﹣2≤2sin（2x+）≤2，﹣1≤2sin（2x+）+1≤3，即﹣1≤f（x）≤3，即f（x）的值域为[﹣1，3]．（2）由2kπ﹣≤2x+≤2kπ+，k∈Z，得kπ﹣≤x≤kπ+，k∈Z，即函数的单调递增区间为[kπ﹣，kπ+]，k∈Z．18．【分析】（1）由相互垂直的直线的系数关系求出a的值；（2）由相互平行的系数关系求出a的值．【解答】解：（1）若l1⊥l2，由题意可得1×（3a﹣1）+2a×（﹣a）＝0，即2a2﹣3a+1＝0，解得a＝或a＝1；（2）若l1∥l2，由题意可得1•（﹣a）＝2a•（3a﹣1），且1×（﹣7）≠1×（3a﹣1），解得a ＝0或a＝．19．【分析】（1）由四边形ABCD是菱形，得AC⊥BD，再由PD⊥平面ABCD，得PD⊥AC，然后利用直线与平面垂直的判定可得AC⊥平面PBD；（2）由PD⊥平面ABCD，得∠PBD是直线PB与平面ABCD所成的角，可得∠PBD＝45°，再由已知求得BD＝2．由AB＝AD＝2，求出菱形ABCD的面积，代入棱锥体积公式求四棱锥P﹣ABCD的体积．【解答】（1）证明：∵四边形ABCD是菱形，∴AC⊥BD，又∵PD⊥平面ABCD，AC⊂平面ABCD，∴PD⊥AC，又PD∩BD＝D，∴AC⊥平面PBD；（2）解：∵PD⊥平面ABCD，∴∠PBD是直线PB与平面ABCD所成的角，于是∠PBD＝45°，∵PD＝2，∴BD＝PD＝2，又AB＝AD＝2，∴菱形ABCD的面积为，故四棱锥P﹣ABCD的体积．20．【分析】（Ⅰ）利用抛物线的性质，直接求p的值；（Ⅱ）联立直线l：y＝x﹣1与抛物线方程，通过韦达定理以及弦长公式，转化求解弦长|AB|．【解答】解：（Ⅰ）由抛物线y2＝2px（p＞0）的准线方程为x＝﹣1．得，所以p＝2；（Ⅱ）设A（x1，y1），B（x2，y2），由消去y，得x2﹣6x+1＝0，则x1+x2＝6，x1x2＝1，所以＝＝＝．21．【分析】（1）将P（﹣2，1）代入+＝1，得椭圆方程为+＝1，设直线AB：y＝kx+m，A（x1，y1），B（x2，y2），A，B的中点为M（x0，y0），由，得（1+4k2）x2+8kmx+4m2﹣8＝0，由此利用韦达定理、中点坐标公式，能求出椭圆C的方程和直线AB 的斜率．（2）当k＝时，由△＝16﹣4m2＞0，得﹣2＜m＜2，x1+x2＝﹣2m，x1x2＝2m2﹣4，|AB|＝|x1﹣x2|＝2•，点P到直线AB：y＝的距离d＝，△P AB面积S＝|AB|d＝|m﹣2|＝，设f（m）＝﹣（m﹣2）3（m+2），（﹣2＜m＜2），利用导数性质能求出△P AB面积的最大值．【解答】解：（1）将P（﹣2，1）代入+＝1，得+＝1，解得a2＝8，∴椭圆方程为+＝1，设直线AB：y＝kx+m，A（x1，y1），B（x2，y2），A，B的中点为M（x0，y0），由，得（1+4k2）x2+8kmx+4m2﹣8＝0，，，直线OP经过弦AB的中点，则k OM＝k OP，＝﹣，＝﹣，∴k AB＝．（2）当k＝时，由△＝16﹣4m2＞0，得﹣2＜m＜2，x1+x2＝﹣2m，x1x2＝2m2﹣4，|AB|＝|x1﹣x2|＝•＝2•，点P到直线AB：y＝的距离d＝，△P AB面积S＝|AB|d＝|m﹣2|＝，设f（m）＝﹣（m﹣2）3（m+2），（﹣2＜m＜2），则f′（m）＝﹣[3（m﹣2）2（m+2）+（m﹣2）3]＝﹣4（m﹣2）2（m+1），解得f（m）max＝f（﹣1）＝27，∴S max＝＝3．22．【分析】（1）根据，设，c＝n，则b＝n，椭圆E的方程为，代入点A的坐标解出即可；（2）设B（x1，y1），C（x2，y2）．直线l：y＝x+m代入椭圆方程并化简，再利用根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式、基本不等式的性质即可得出．【解答】解：（1）因为，所以设，c＝n，则b＝n，椭圆E的方程为．代入点A的坐标得，n2＝1，所以椭圆E的方程为．…（4分）（2）设点B，C的坐标分别为（x1，y1），（x2，y2），由得，即，，…（6分）△＝2m2﹣4（m2﹣1）＞0，m2＜2．…（7分）＝＝，点A到直线l的距离，…（9分）△ABC的面积＝＝…（11分），当且仅当m2＝2﹣m2，即m2＝1时等号成立．所以当m＝±1时，△ABC面积的最大值为．…（12分）。

江苏省南京航空航天大学附属高级中学2020-2021学年度高三第一学期期中考试数学本试卷满分150分，考试时间120分钟一、单项选择题（本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求）1．已知集合A ={}22|≤≤-x x ，B =(){}1lg |-=x y x ，则B A =（ ）A.{}2|-≥x x B ．{}21|<<x x C ．{}21|≤<x x D ．{}2|≥x x2．若复数i i z +-=⋅1，则复数z 的虚部为（ ）A ．－1B ．1C ．－iD ．i3．矩形ABCD 中，AB=2，AD=1，E ，F 分别是边AB ，CD 的中点，将正方形ADFE 沿EF 折到A 1D 1FE 位置，使得二面角A 1-EF-B 的大小为120°，则异面直线A 1F 与CE 所成角的余弦值为（ ）A ．105B ．1010C ．21D ．43 4．朱载堉(1536-1611)，明太祖九世孙，音乐家、数学家、天文历算家，在他多达百万字的著述中以《乐律全书》最为著名， 在西方人眼中他是大百科全书式的学者王子。

他对文艺的最大贡献是他创建了“十二平均律”，此理论被广泛应用在世界各国的键盘乐器上，包括钢琴，故朱载墒被誉为“钢琴理论的鼻祖”。

“十二平均律”是指一个八度有13个音，相邻两个音之间的频率之比相等，且最后一个音频率是最初那个音频率的2倍，设第二个音的频率为f 2，第八个音的频率为f 8，则28f f 等于（ ） A ．2 B ．32 C ．42 D ．625．已知4tan 1tan =+θθ，则⎪⎭⎫ ⎝⎛+4cos 2πθ=（ ） A ．51B ．41C ．31D ．21 6．已知P 是椭圆()012222>>=+b a by a x 上的一点，F 1、F 2分别是椭圆的左、右焦点，点P 到原点O 的距离为焦距的一半，且|PF 1|－|PF 2|=a ，则椭圆的离心率为（ ）A ．46B ．410C ．23D ．22 7．已知实数a ，b ，c 满足ca b 110lg ==，则下列关系式中不可能成立的是（ ） A ．a >b >c B ．a >c >b C ．c >a >b D ．c >b >a8．设函数()2ln 2+-=x x x x f ，若存在区间[]⎪⎭⎫⎢⎣⎡∞+⊆，，21b a ，使得()x f 在[]b a ，上的值域为()()[]22++b k a k ，，则实数k 的取值范围是（ ）A ．⎪⎭⎫ ⎝⎛+42ln 391，B ．⎥⎦⎤⎢⎣⎡+42ln 391，C ．⎥⎦⎤ ⎝⎛+102ln 291，D ．⎥⎦⎤⎢⎣⎡+102ln 291， 二、多项选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求，请把答案填涂在答题卡相应位置上．全部选对得5分，部分选对得3分，不选或有错选的得0分．9．港珠澳大桥位于中国广东省珠江口伶仃洋海域内，是中国境内一项连接香港、珠海和澳门的桥隊工程，因其超大的建筑规模、空前的施工难度和顶尖的建造技术而闻名世.2018年10月24日上午9时开通运营后香港到澳门之间4个小时的陆路车程极大缩矩.为了解实际通行所需时间，随机抽取了n 台车辆进行统计，结果显示这些车辆的通行时间(单位:分钟)都在[35, 50]内，按通行时间分为[35,38) ，[38,41) ，[41,44)，[44, 47)，[47,50]五组，其中通行时间在[38,47)的车辆有182台，频率分布直方图如图所示，则（ ）A.n =200B.n =280C.抽取的车辆中通行时间在[35,38)的车辆有4台D.抽取的车辆中通行时间在[35,38)的车辆有12台10．已知曲线C 的方程为()R k ky k x ∈=-+-16222，则下列结论正确的是（ ） A ．当k =4时，曲线C 为圆B ．当k =0时，曲线C 为双曲线，其渐近线方程为x y 3±=C ．“5<k <6”是“曲线C 为焦点在x 轴上的椭圆”的充分不必要条件D ．存在实数k 使得曲线C 为双曲线，其离心率为211．已知等差数列{}n a 的首项为1，公差d =4，前n 项和为n S ，则下列结论成立的是（ ）A ．数列⎭⎬⎫⎩⎨⎧n S n 的前10项和为100 B ．若a 1，a 3，a m 成等比数列，则m =21C ．若256111>∑=+n i i i a a ，则n 的最小值为6 D ．若a m +a n =a 2+a 10，则n m 161+的最小值为1225 12．已知棱长为1的正方体ABCD -A 1B 1C 1D 1，过对角线BD 1作平面α交棱AA 1于点E ，交棱CC 1于点F ，以下结论正确的是（ ）A ．四边形BFD 1E 不一定是平行四边形B ．平面α分正方体所得两部分的体积相等C ．平面α于平面DBB 1不可能垂直D ．四边形BFD 1E 面积的最大值为2三、填空题：本大题共4小题，每小题5分，共20分．请把答案填写在答题卡相应位置上．13．已知平面向量a =（1，0），b =（21-，23），则a 与a +b 的夹角为▲________． 14．回文联是我国对联中的一种.用回文形式写成的对联，既可顺读，也可倒读.不仅意思不变，而且颇具趣味.相传，清代北京城里有一家饭馆叫“天然居”，曾有一副有名的回文联：“客上天然居，居然天上客；人过大佛寺，寺佛大过人."”在数学中也有这样一类顺读与倒读都是同一个数的自然数，称之为“回文数”.如44， 585，2662等；那么用数字1，2，3，4， 5，6可以组成4位“回文数”的个数为▲________．15．设函数()()⎪⎭⎫ ⎝⎛<>+=20sin 2πϕϕϕω，x x f 的部分图象如图．若对任意的()()x t f x f R x -=∈2，恒成立，则实数t 的最小正值为▲________．16．在平面直角坐标系xOy 中，过点P 向圆O ：422=+y x 和圆C ：()()42222=-++y x 各引一条切线，切点分别为A ，B ，若PB =2P A ，且平面上存在一定点M ，使得P 到M 的距离为定值。

2020-2021学年江苏省南航附中高三（上）质检数学试卷（10月份）试题数：22.满分：01.（单选题.3分）已知集合P={x|x2≤1}.M={a}．若P∪M=P.则a的取值范围是（）A.（-∞.-1]B.[1.+∞）C.[-1.1]D.（-∞.-1]∪[1.+∞）2.（单选题.3分）设a∈R.若复数（1+i）（a+i）在复平面内对应的点位于实轴上.则a=（）A.0B.-1C.1D. √23.（单选题.3分）若f（x）=tan（ωx）（ω＞0）的最小正周期为1.则f(1)的值为（）3A. −√3B. −√33C. √33D. √34.（单选题.3分）下列函数中.值域为R且为奇函数的是（）A.y=x+2B.y=sinxC.y=x-x3D.y=2x5.（单选题.3分）设a⃗ . b⃗⃗均为单位向量.则“| a⃗ -3 b⃗⃗ |=|3 a⃗ + b⃗⃗|”是“ a⃗⊥ b⃗⃗”的（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件6.（单选题.3分）将4位志愿者分配到世博会的3个不同场馆服务.每个场馆至少1人.不同的分配方案有（）种．A.72B.36C.64D.817.（单选题.3分）若f （x ）=Asin （ωx+φ）（其中A ＞0.|φ| ＜π2 ）的图象如图.为了得到 g (x )=sin (2x −π3) 的图象.则需将f （x ）的图象（ ）A.向右平移 π6个单位B.向右平移 π3 个单位 C.向左平移 π6 个单位 D.向左平移 π3 个单位8.（单选题.3分）2020年3月14日是全球首个国际圆周率日（π Day ）．历史上.求圆周率π的方法有多种.与中国传统数学中的“割圆术”相似.数学家阿尔•卡西的方法是：当正整数n 充分大时.计算单位圆的内接正6n 边形的周长和外切正6n 边形（各边均与圆相切的正6n 边形）的周长.将它们的算术平均数作为2π的近似值．按照阿尔•卡西的方法.π的近似值的表达式是（ ） A.3n （sin 30°n +tan 30°n ） B.6n （sin 30°n +tan 30°n） C.3n （sin60°n +tan 60°n ） D.6n （sin60°n +tan 60°n） 9.（多选题.3分）Keep 是一款具有社交属性的健身APP.致力于提供健身教学、跑步、骑行、交友及健身饮食指导、装备购买等一站式运动解决方案．Keep 可以让你随时随地进行锻炼.记录你每天的训练进程．不仅如此.它还可以根据不同人的体质.制定不同的健身计划．小明根据Keep 记录的2019年1月至2019年11月期间每月跑步的里程（单位：十公里）数据整理并绘制了下面的折线图．根据该折线图.下列结论正确的是（ ）A.月跑步里程最小值出现在2月B.月跑步里程逐月增加C.月跑步里程的中位数为5月份对应的里程数D.1月至5月的月跑步里程相对于6月至11月波动性更小10.（多选题.3分）已知圆锥的顶点为P.母线长为2.底面半径为√3 .A.B为底面圆周上两个动点.则下列说法正确的是（）A.圆锥的高为1B.三角形PAB为等腰三角形C.三角形PAB面积的最大值为√3D.直线PA与圆锥底面所成角的大小为π611.（多选题.3分）台球运动已有五、六百年的历史.参与者用球杆在台上击球．若和光线一样.台球在球台上碰到障碍物后也遵从反射定律．如图.有一张长方形球台ABCD.AB=2AD.现从角落A沿角α的方向把球打出去.球经2次碰撞球台内沿后进入角落C的球袋中.则tanα的值为（）A. 16B. 12C.1D. 3212.（多选题.3分）函数y=f（x）图象上不同两点A（x1.y1）.B（x2.y2）处的切线的斜率分别叫曲线y=f（x）在点A与点B之间的“弯曲度”.以下正确的命是k A.k B.规定φ（A.B）= |k A−k B||AB|题为（）A.函数y=x3-x2+1图象上两点A、B的横坐标分别为1.2.则φ(A，B)＞√3B.存在这样的函数.图象上任意两点之间的“弯曲度”为常数C.设点A 、B 是抛物线.y=x 2+1上不同的两点.则φ（A.B ）⩽2D.设曲线y=e x 上不同两点A （x 1.y 1）.B （x 2.y 2）.且x 1-x 2=1.若t•ϕ（A.B ）＜1恒成立.则实数t 的取值范围是（-∞.1）13.（填空题.3分）设S n 为等差数列{a n }的前n 项和.a 1=3.S 3=18.则其通项公式a n =___ ． 14.（填空题.3分）已知tan （α+β）= 25 .tan （β- π4 ）= 14 .则tan （α+ π4 ）=___ ．15.（填空题.3分）如图.已知正方形OABC.其中OA=a （a ＞1）.函数y=3x 2交BC 于点P.函数 y =x −12交AB 于点Q.当|AQ|+|CP|最小时.则a 的值为 ___ ．16.（填空题.3分）设函数f （x ）=me x -x 2+3.其中m∈R ．若函数f （x ）在区间[-2.4]上有三个零点.则m 的取值范围为___ ． 17.（问答题.0分）从 ① sinA= √1010 . ② cosB= −√55. ③ b=4这三个条件中任选一个.补充在问题中并作答．在△ABC 中.a= √2 .c= √10 .且____．（补充条件） （1）求△ABC 的面积； （2）求sin （A+B ）．18.（问答题.0分）已知向量 a ⃗ =（2cosx.2sinx ）. b ⃗⃗ =（ √3 cosx.cosx ）.设函数f （x ）= a ⃗•b ⃗⃗ - √3 .求：（1）f （x ）的最小正周期和单调递增区间；（2）若 f (α2−π6)−f (α2+π12)=√6 .且α∈（ π2 .π）．求α．19.（问答题.0分）2018年11月5日上午.首届中国国际进口博览会拉开大幕.这是中国也是世界上首次以进口为主题的国家级博览会．本次博览会包括企业产品展、国家贸易投资展．其中企业产品展分为7个展区.每个展区统计了备受关注百分比.如表：展区类型智能及高端装备消费电子及家电汽车服装服饰及日用消费品食品及农产品医疗器械及医药保健服务贸易展区的企业数（家）400 60 70 650 1670 300 450备受关注百分比25% 20% 10% 23% 18% 8% 24% 备受关注百分比指：一个展区中受到所有相关人士关注（简称备受关注）的企业数与该展区的企业数的比值．（Ⅰ）从企业产品展7个展区的企业中随机选取1家.求这家企业是选自“智能及高端装备”展区备受关注的企业的概率；（Ⅱ）从“消费电子及家电”展区备受关注的企业和“医疗器械及医药保健”展区备受关注的企业中.任选2家接受记者采访．（ i）记X为这2家企业中来自于“消费电子及家电”展区的企业数.求随机变量X的分布列；（ii）假设表格中7个展区的备受关注百分比均提升10%．记Y为这2家企业中来自于“消费电子及家电”展区的企业数．试比较随机变量X.Y的均值E（X）和E（Y）的大小．（只需写出结论）20.（问答题.0分）如图.在四棱锥P-ABCD中.PA⊥底面ABCD.AD ||BC.AB=AC=AD=3.PA=BC=4．（1）求异面直线PB与CD所成角的余弦值；（2）求平面PAD与平面PBC所成锐二面角的余弦值．21.（问答题.0分）已知函数f（x）=lnx-ax2+2ax．（Ⅰ）若a=-1.求曲线y=f（x）在点（1.f（1））处的切线方程；（Ⅱ）若f（x）≤x恒成立.求实数a的取值范围．22.（问答题.0分）已知函数f（x）=（3-x）e x.g（x）=x+a（a∈R）（e是自然对数的底数.e≈2.718…）．（1）求函数f（x）的极值；（2）若函数y=f（x）g（x）在区间[1.2]上单调递增.求a的取值范围；在区间（0.+∞）上既存在极大值又存在极小值.并且h（x）的（3）若函数h（x）= f(x)+g(x)x极大值小于整数b.求b的最小值．2020-2021学年江苏省南航附中高三（上）质检数学试卷（10月份）参考答案与试题解析试题数：22.满分：01.（单选题.3分）已知集合P={x|x2≤1}.M={a}．若P∪M=P.则a的取值范围是（）A.（-∞.-1]B.[1.+∞）C.[-1.1]D.（-∞.-1]∪[1.+∞）【正确答案】：C【解析】：通过解不等式化简集合P；利用P∪M=P⇔M⊆P；求出a的范围．【解答】：解：∵P={x|x2≤1}.∴P={x|-1≤x≤1}∵P∪M=P∴M⊆P∴a∈P-1≤a≤1故选：C．【点评】：本题考查不等式的解法、考查集合的包含关系：根据条件P∪M=P⇔M⊆P是解题关键．2.（单选题.3分）设a∈R.若复数（1+i）（a+i）在复平面内对应的点位于实轴上.则a=（）A.0B.-1C.1D. √2【正确答案】：B【解析】：利用复数代数形式的乘除运算化简.再由虚部为0求解a值．【解答】：解：∵复数（1+i）（a+i）=（a-1）+（a+1）i在复平面内对应的点位于实轴上.∴a+1=0.即a=-1．故选：B．【点评】：本题考查复数代数形式的乘除运算.考查复数的代数表示法及其几何意义.是基础题．3.（单选题.3分）若f（x）=tan（ωx）（ω＞0）的最小正周期为1.则f(13)的值为（）A. −√3B. −√33C. √33D. √3【正确答案】：D【解析】：由题意利用正切函数的周期性求得ω的值.可得它的解析式.从而求出f(13)的值．【解答】：解：∵f（x）=tan（ωx）（ω＞0）的周期为πω=1.∴ω=π.即f（x）=tanπx.则f(13) =tan π3= √3 .故选：D．【点评】：本题主要考查正切函数的周期性.属于基础题．4.（单选题.3分）下列函数中.值域为R且为奇函数的是（）A.y=x+2B.y=sinxC.y=x-x3D.y=2x【正确答案】：C【解析】：分别结合奇偶性及函数的值域判断各选项即可求解．【解答】：解：A：y=x+2为非奇非偶函数.不符合题意；B：y=sinx的值域[-1.1].不符合题意；C：y=x-x3为奇函数且值域为R.符合题意；D：y=2x为非奇非偶函数.不符合题意．故选：C．【点评】：本题主要考查了基本初等函数的奇偶性的判断及值域的求解.属于基础试题．5.（单选题.3分）设a⃗ . b⃗⃗均为单位向量.则“| a⃗ -3 b⃗⃗ |=|3 a⃗ + b⃗⃗|”是“ a⃗⊥ b⃗⃗”的（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【正确答案】：C【解析】：根据向量数量积的应用.结合充分条件和必要条件的对应进行判断即可．【解答】：解：∵“| a⃗ -3 b⃗⃗ |=|3 a⃗ + b⃗⃗|”∴平方得| a⃗|2+9| b⃗⃗ |2-6 a⃗• b⃗⃗ =9| a⃗|2+| b⃗⃗ |2+6 a⃗• b⃗⃗ .即1+9-6 a⃗• b⃗⃗ =9+1+6 a⃗• b⃗⃗ .即12 a⃗• b⃗⃗ =0.则a⃗• b⃗⃗ =0.即a⃗⊥ b⃗⃗ .反之也成立.则“| a⃗ -3 b⃗⃗ |=|3 a⃗ + b⃗⃗|”是“ a⃗⊥ b⃗⃗”的充要条件.故选：C．【点评】：本题主要考查充分条件和必要条件的判断.结合向量数量积的公式进行转化是解决本题的关键．6.（单选题.3分）将4位志愿者分配到世博会的3个不同场馆服务.每个场馆至少1人.不同的分配方案有（）种．A.72B.36C.64D.81【正确答案】：B【解析】：先从4个人中选出2个作为一个元素看成整体.再把它同另外两个元素在三个位置全排列.根据分步乘法原理得到结果【解答】：解：∵将4位志愿者分配到3个不同场馆服务.每个场馆至少1人.∴先从4个人中选出2个作为一个元素看成整体.再把它同另外两个元素在三个位置全排列.共有C24A33=36．故选：B．【点评】：本题考查排列组合及简单的计数问题.是一个基础题.本题又是一个易错题.排列容易重复.注意做到不重不漏．7.（单选题.3分）若f（x）=Asin（ωx+φ）（其中A＞0.|φ| ＜π2）的图象如图.为了得到g(x)=sin(2x−π3)的图象.则需将f（x）的图象（）A.向右平移π6个单位B.向右平移π3个单位C.向左平移π6个单位D.向左平移π3个单位【正确答案】：B【解析】：由函数的图象的顶点坐标求出A.由周期求出ω.由五点法作图求出φ的值.可得函数的解析式.再利用y=Asin（ωx+φ）的图象变换规律.得出结论．【解答】：解：根据f（x）=Asin（ωx+ϕ）（其中A＞0.|φ| ＜π2）的图象.可得A=1.1 4•2πω= 7π12- π3.∴ω=2．再根据五点法作图可得2• π3+φ=π.∴φ= π3.∴f（x）=sin（2x+ π3）．故把f（x）=sin（2x+ π3）的图象向右平移π3个单位.可得y=sin[2（x- π3）+ π3]=sin（2x- π3）=g（x）的图象.故选：B．【点评】：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式.由函数的图象的顶点坐标求出A.由周期求出ω.由五点法作图求出φ的值.y=Asin（ωx+φ）的图象变换规律.属于基础题．8.（单选题.3分）2020年3月14日是全球首个国际圆周率日（π Day）．历史上.求圆周率π的方法有多种.与中国传统数学中的“割圆术”相似.数学家阿尔•卡西的方法是：当正整数n充分大时.计算单位圆的内接正6n边形的周长和外切正6n边形（各边均与圆相切的正6n边形）的周长.将它们的算术平均数作为2π的近似值．按照阿尔•卡西的方法.π的近似值的表达式是（ ） A.3n （sin 30°n +tan 30°n） B.6n （sin 30°n +tan 30°n） C.3n （sin60°n +tan 60°n ） D.6n （sin60°n +tan 60°n） 【正确答案】：A【解析】：设内接正6n 边形的边长为a.外切正6n 边形的边长为b.运用圆的性质.结合直角三角形的锐角三角函数的定义.可得所求值．【解答】：解：如图.设内接正6n 边形的边长为a.外切正6n 边形的边长为b. 可得a=2sin 360°12n =2sin 30°n. b=2tan 360°12n =2tan 30°n. 则2π≈6na+6nb 2 =6n （sin 30°n +tan 30°n）. 即π≈3n （sin 30°n +tan 30°n）. 故选：A ．【点评】：本题考查数学中的文化.考查圆的内接和外切多边形的边长的求法.考查运算能力.属于基础题．9.（多选题.3分）Keep 是一款具有社交属性的健身APP.致力于提供健身教学、跑步、骑行、交友及健身饮食指导、装备购买等一站式运动解决方案．Keep 可以让你随时随地进行锻炼.记录你每天的训练进程．不仅如此.它还可以根据不同人的体质.制定不同的健身计划．小明根据Keep 记录的2019年1月至2019年11月期间每月跑步的里程（单位：十公里）数据整理并绘制了下面的折线图．根据该折线图.下列结论正确的是（ ）A.月跑步里程最小值出现在2月B.月跑步里程逐月增加C.月跑步里程的中位数为5月份对应的里程数D.1月至5月的月跑步里程相对于6月至11月波动性更小【正确答案】：ACD【解析】：由所给折线图可知.月跑步里程并不是逐递增.月跑步里程最小值出现在2月.月跑步里程中位数为5月份对应的里程数.1月至5月的月跑步里程相对于6月至11月.波动性更小．【解答】：解：由所给折线图可知.月跑步里程并不是逐递增.故B错误；月跑步里程最小值出现在2月.故A正确；月跑步里程中位数为5月份对应的里程数.故C正确；1月至5月的月跑步里程相对于6月至11月.波动性更小.故D正确．故选：ACD．【点评】：本题考查命题真假的判断.考查折线图的性质等基础知识.考查运算求解能力.是基础题．10.（多选题.3分）已知圆锥的顶点为P.母线长为2.底面半径为√3 .A.B为底面圆周上两个动点.则下列说法正确的是（）A.圆锥的高为1B.三角形PAB为等腰三角形C.三角形PAB面积的最大值为√3D.直线PA与圆锥底面所成角的大小为π6【正确答案】：ABD【解析】：直接利用勾股定理的应用求出圆锥的高.进一步判定三角形的形状和直线与平面的夹角．【解答】：解：圆锥的顶点为P.母线长为2.底面半径为√3 .如图所示：所以圆锥的高为h= √(2)2−(√3)2=1．故选项A正确．由于A和B为底面圆周上两个动点.由于满足PA=PB.所以△PAB为等腰三角形.故选项B正确．由于S△PAB=12×2×2×sin∠APB .当sin∠APB=1时.三角形PAB面积的最大值为2．直线PA与圆锥底面所成角为直线PA和AO所成的角.即∠PAO.在△APO中.sin ∠PAO=POAP =12.所以∠PAO=π6．故选项D正确．故选：ABD．【点评】：本题考查的知识要点：圆锥的性质的应用.直线与平面的夹角的应用.主要考查学生的运算能力和转换能力及思维能力.属于基础题型．11.（多选题.3分）台球运动已有五、六百年的历史.参与者用球杆在台上击球．若和光线一样.台球在球台上碰到障碍物后也遵从反射定律．如图.有一张长方形球台ABCD.AB=2AD.现从角落A沿角α的方向把球打出去.球经2次碰撞球台内沿后进入角落C的球袋中.则tanα的值为（）A. 16B. 12C.1D. 32【正确答案】：AD【解析】：根据题意画出示意图.进而求解结论．【解答】：解：因为AB=2AD.现从角落A沿角α的方向把球打出去.球经2次碰撞球台内沿后进入角落C的球袋中；当是图一时.如图：A关于DC 的对称点为E.C关于AB的对称点为F；如图；根据直线的对称性可得：tanα= EGGF = 3AD2AD= 32；当是图2时.如图：A关于BC 的对称点为G.C关于AD的对称点为E.如图：根据直线的对称性可得：tanα= EFFG = AD6AD= 16；故选：AD．【点评】：本题主要考查直线的对称性.属于基础题目．12.（多选题.3分）函数y=f（x）图象上不同两点A（x1.y1）.B（x2.y2）处的切线的斜率分别是k A.k B.规定φ（A.B）= |k A−k B||AB|叫曲线y=f（x）在点A与点B之间的“弯曲度”.以下正确的命题为（）A.函数y=x3-x2+1图象上两点A、B的横坐标分别为1.2.则φ(A，B)＞√3B.存在这样的函数.图象上任意两点之间的“弯曲度”为常数C.设点A、B是抛物线.y=x2+1上不同的两点.则φ（A.B）⩽2D.设曲线y=e x 上不同两点A （x 1.y 1）.B （x 2.y 2）.且x 1-x 2=1.若t•ϕ（A.B ）＜1恒成立.则实数t 的取值范围是（-∞.1） 【正确答案】：BC【解析】：根据定义计算φ（A.B ）判断A.以一次函数为例判断B.根据φ（A.B ）的计算式判断C.讨论t 的符号.求出 1φ(A ，B)的取值范围.从而可得出t 的范围判断D ．【解答】：解：对于A.y′=3x 2-2x.故k A =1.k B =8.又A （1.1）.B （2.5）.故|AB|= √17 . ∴φ（A.B ）=√17＜ √3 .故A 错误；对于B.若f （x ）为一次函数.则函数图象上任意两点处的切线斜率都相等.故φ（A.B ）=0.故B 正确；对于C.y′=2x .故φ（A.B ）=12√(x 1−x 2)2+(y 1−y 2)2.当且仅当y 1=y 2时取等号.故C 正确；对于D.由定义可知φ（A.B ）≥0.故当t≤0时.t•ϕ（A.B ）＜1恒成立.符合题意. 当t ＞0时.由t•ϕ（A.B ）＜1恒成立可知t ＜ 1φ(A ，B)恒成立.而1φ(A ，B) = |AB||e x 1−ex 2| =√1+(e x 1−e x 2)2e x 1−e x 2.令e x 1-e x 2=m.则m ＞0.1φ(A ，B)=√1+(e x 1−e x 2)2e x 1−e x 2= √m 2+1m = √1m2+1 ＞1.∴0＜t≤1.综上.t 的取值范围是（-∞.1].故D 错误． 故选：BC ．【点评】：本题考查了对新定义的理解.导数的几何意义.函数值域的计算.属于中档题． 13.（填空题.3分）设S n 为等差数列{a n }的前n 项和.a 1=3.S 3=18.则其通项公式a n =___ ． 【正确答案】：[1]3n【解析】：运用等差数列的前n 项和公式可解决此问题．【解答】：解：根据题意得.a 1=3.S 3=a 1+a 2+a 3=18. ∴3a 2=18. ∴a 2=6. ∴d=3.∴a n =3+3（n-1）=3n. 故答案为：3n ．【点评】：本题考查等差数列的前n 项和公式和等差数列的通项公式．14.（填空题.3分）已知tan （α+β）= 25 .tan （β- π4 ）= 14 .则tan （α+ π4 ）=___ ． 【正确答案】：[1] 322【解析】：由条件利用两角差的正切公式求得tan （α+ π4 ）的值．【解答】：解：∵tan （α+β）= 25 .tan （β- π4 ）= 14 .∴tan （α+ π4 ）= tan (α+β)−tan(β−π4)1+tan (α+β)•tan(β−π4)= 25−141+25×14= 322 .【点评】：本题主要考查两角差的正切公式的应用.属于基础题．15.（填空题.3分）如图.已知正方形OABC.其中OA=a （a ＞1）.函数y=3x 2交BC 于点P.函数 y =x −12交AB 于点Q.当|AQ|+|CP|最小时.则a 的值为 ___ ．【正确答案】：[1] √3【解析】：由已知可得P.Q 坐标.进而可得|AQ|+|CP|= √a3 + √1a .由基本不等式可得答案．【解答】：解：由题意得：P 点坐标为（ √a3 .a ）.Q 点坐标为（a. √1a ）. |AQ|+|CP|= √a3 + √1a ≥2 √√3.当且仅当a= √3 时.取最小值. 故答案为： √3 ．【点评】：本题考查的知识点是基本不等式.二次函数和幂函数.难度不大.属于基础题． 16.（填空题.3分）设函数f （x ）=me x -x 2+3.其中m∈R ．若函数f （x ）在区间[-2.4]上有三个零点.则m 的取值范围为___ ． 【正确答案】：[1][ 13e 4 . 6e 3 ）【解析】：由题意可得me x -x 2+3=0在[-2.4]上有三个不等的实根.等价为m= x 2−3e x在[-2.4]上有三个不等的实根．设g （x ）=x 2−3e x.求得导数和单调性.可得极值和最值.画出y=g （x ）在[-2.4]的图象.通过图象可得所求范围．【解答】：解：函数f （x ）在区间[-2.4]上有三个零点. 即为me x -x 2+3=0在[-2.4]上有三个不等的实根. 等价为m= x 2−3e x在[-2.4]上有三个不等的实根． 设g （x ）= x 2−3e x .g′（x ）= 2x−x 2+3e x =- (x−3)(x+1)e x. 可得g （x ）在[-2.-1]递减.在（-1.3）递增.在[3.4]递减.则g （x ）的最小值为g （-1）=-2e.g （x ）的极大值为g （3）= 6e 3 . g （4）= 13e4 .画出y=g （x ）在[-2.4]的图象. 可得当 13e 4 ≤m ＜ 6e 3 时.y=m 和y= x 2−3e x在[-2.4]上有三个不同的交点. 故答案为：[ 13e 4 . 6e3 ）．【点评】：本题考查函数零点个数问题.考查数形结合思想和转化思想.运算能力和推理能力.属于中档题．17.（问答题.0分）从 ① sinA= √1010 . ② cosB= −√55. ③ b=4这三个条件中任选一个.补充在问题中并作答．在△ABC 中.a= √2 .c= √10 .且____．（补充条件） （1）求△ABC 的面积； （2）求sin （A+B ）．【正确答案】：【解析】：若选择 ① .依题意.利用同角三角函数基本关系式可求cosA.由余弦定理可解得b 的值.（1）利用三角形的面积公式即可求解；（2）由已知利用正弦定理可求sinC 的值.结合两角和的正弦函数公式可求sin （A+B ）的值．若选择 ② .（1）利用同角三角函数基本关系式可求sinB.进而根据三角形的面积公式即可求解；（2）由已知利用余弦定理可求b 的值.利用正弦定理可求sinC 的值.例两角和的正弦函数公式即可求解sin （A+B ）的值．若选择 ③ .（1）由余弦定理可得cosC 的值.利用同角三角函数基本关系式可求sinC 的值.利用三角形的面积公式即可得解；（2）根据两角和的正弦函数公式即可求解sin （A+B ）的值．【解答】：解：若选择 ① . 依题意.A 为锐角.由sinA=√1010.得cosA= √1−sin 2A =3√1010. 在△ABC 中.因为a= √2 .c= √10 .由余弦定理a 2=b 2+c 2-2bccosA.可得：（ √2 ）2=b 2+（ √10 ）2-2× √10×3√1010b .解得b=2或b=4.（1）当b=2时.S △ABC = 12 bcsinA= 12×2×√10×√1010=1；当b=4时.S △ABC =2；（2）由a= √2 .c= √10 .sinA= √1010 . asinA =csinC .可得sinC= √22 . 在△ABC 中.A+B=π-C.sin （A+B ）=sinC= √22． 若选择 ② .（1）因为cosB=- √55.B∈（0.π）.所以sinB= √1−cos 2B = 2√55. 因为a= √2 .c= √10 .所以S △ABC = 12 acsinB= 12×√2×√10×2√55=2．（2）因为a= √2 .c= √10 .cosB=- √55.由b2=a2+c2-2accosB.可得：b2=（√2）2+（√10）2-2× √2×√10×（- √55）=16.解得b=4.由bsinB =csinC.解得sinC= √22.在△ABC中.A+B=π-C.sin（A+B）=sinC= √22．若选择③ .（1）在△ABC中.因为a= √2 .c= √10 .b=4.由余弦定理可得cosC= a 2+b2−c22ab=2×√2×4= √22.因为C∈（0.π）.所以sinC= √1−cos2C = √22.所以S△ABC= 12 absinC= 12×√2×4×√22=2．（2）在△ABC中.A+B=π-C.sin（A+B）=sinC= √22．【点评】：本题主要考查了同角三角函数基本关系式.三角形的面积公式.正弦定理.两角和的正弦函数公式.余弦定理在解三角形中的综合应用.考查了计算能力和转化思想.属于中档题18.（问答题.0分）已知向量a⃗ =（2cosx.2sinx）. b⃗⃗ =（√3 cosx.cosx）.设函数f（x）= a⃗•b⃗⃗ - √3 .求：（1）f（x）的最小正周期和单调递增区间；（2）若f(α2−π6)−f(α2+π12)=√6 .且α∈（π2.π）．求α．【正确答案】：【解析】：（1）f（x）解析式利用平面向量的数量积运算法则计算.再利用二倍角的正弦、余弦函数公式化简.整理后找出ω的值.代入周期公式即可求出最小正周期；由正弦函数的递增区间即可确定出f（x）的递增区间；（2）利用f（x）解析式化简已知等式求出sin（α- π4）的值.根据α的范围即可确定出α的度数．【解答】：解：f（x）= a⃗• b⃗⃗ - √3 =2 √3 cos2x+2sinxcosx- √3 =sin2x+ √3 cos2x=2sin（2x+ π3）；（1）∵ω=2.∴函数f（x）的最小正周期为T= 2π2π；由2kπ- π2≤2x+ π3≤2kπ+ π2.k∈Z.得kπ- 5π12≤x≤kπ+ π12.k∈Z.∴函数f（x）的单调递增区间为[kπ- 5π12 .kπ+ π12].k∈Z；（2）∵f（α2 - π6）-f（α2+ π12）= √6 .∴2sinα-2cosα= √6 .∴2 √2 sin（α- π4）= √6 .∴sin（α- π4）= √32.∵α∈（π2 .π）.∴α- π4∈（π4. 3π4）.∴α- π4 = π3或2π3.∴α= 7π12或11π12．【点评】：此题考查了三角函数中的恒等变换应用.以及平面向量数量积的运算.熟练掌握运算法则是解本题的关键．19.（问答题.0分）2018年11月5日上午.首届中国国际进口博览会拉开大幕.这是中国也是世界上首次以进口为主题的国家级博览会．本次博览会包括企业产品展、国家贸易投资展．其中企业产品展分为7个展区.每个展区统计了备受关注百分比.如表：企业数的比值．（Ⅰ）从企业产品展7个展区的企业中随机选取1家.求这家企业是选自“智能及高端装备”展区备受关注的企业的概率；（Ⅱ）从“消费电子及家电”展区备受关注的企业和“医疗器械及医药保健”展区备受关注的企业中.任选2家接受记者采访．（ i）记X为这2家企业中来自于“消费电子及家电”展区的企业数.求随机变量X的分布列；（ii）假设表格中7个展区的备受关注百分比均提升10%．记Y为这2家企业中来自于“消费电子及家电”展区的企业数．试比较随机变量X.Y 的均值E （X ）和E （Y ）的大小．（只需写出结论）【正确答案】：【解析】：（Ⅰ）根据题意计算对应的频率值.用频率估计概率即可； （Ⅱ）由题意知X 的可能取值.计算对应的概率值.写出它的分布列； （Ⅲ）结合题意得出E （X ）＞E （Y ）．【解答】：解：（Ⅰ）7个展区企业数共400+60+70+650+1670+300+450=3600家. 其中备受关注的智能及高端装备企业共400×25%=100家.设从各展区随机选1家企业.这家企业是备受关注的智能及高端装备为事件A. 所以P （A ）=1003600 = 136；………………（4分）（Ⅱ）消费电子及家电备受关注的企业有60×20%=12（家）. 医疗器械及医药保健备受关注的企业有300×8%=24（家）.共36家． ∴X 的可能取值为0.1.2； 计算P （X=0）= C 242C 362 = 46105 .P （X=1）=C 121•C 241C 362 = 1635. P （X=2）= C 122C 362 = 11105 ；所以随机变量X 的分布列为：（Ⅲ）计算E （X ）.结合题意知E （X ）＞E （Y ）． …………（13分）【点评】：本题考查了古典概型的概率计算问题.也考查了离散型随机变量的分布列计算问题.是中档题．20.（问答题.0分）如图.在四棱锥P-ABCD 中.PA⊥底面ABCD.AD || BC.AB=AC=AD=3.PA=BC=4．（1）求异面直线PB 与CD 所成角的余弦值；（2）求平面PAD 与平面PBC 所成锐二面角的余弦值．【正确答案】：【解析】：（1）设BCr 中点为E.由AB=AC.得AE⊥BC .以AE.AD.AP 所在的直线分别为x.y.z 轴.建立空间直角坐标系.利用向量法能求出异面直线PB 与CD 所成角的余弦值．（2）求出平面PBC 的法向量和平面PAD 的一个法向量.利用向量法能求出平面PAD 与平面PBC 所成锐二面角的余弦值．【解答】：解：（1）设BCr 中点为E.由AB=AC.得AE⊥BC . ∴以AE.AD.AP 所在的直线分别为x.y.z 轴.建立空间直角坐标系.如图. 则A （0.0.0）.P （0.0.4）.D （0.3.0）.B （ √5，−2，0 ）.C （ √5 .2.0）. 设异面直线PB 与CD 所成角为θ. 则cosθ= |PB ⃗⃗⃗⃗⃗⃗•CD ⃗⃗⃗⃗⃗⃗||PB ⃗⃗⃗⃗⃗⃗|•|CD ⃗⃗⃗⃗⃗⃗| = √25•√6= 7√630 ． ∴异面直线PB 与CD 所成角的余弦值为 7√630 ． （2）设平面PBC 的法向量 n ⃗⃗ =（x.y.z ）.PB ⃗⃗⃗⃗⃗⃗ =（ √5，−2，−4 ）. PC ⃗⃗⃗⃗⃗⃗ =（ √5，2，−4 ）. 由 {PB ⃗⃗⃗⃗⃗⃗•n ⃗⃗=√5x −2y −4z =0PC ⃗⃗⃗⃗⃗⃗•n ⃗⃗=√5x +2y −4z =0 .取x=4.得 n ⃗⃗ =（4.0. √5 ）.平面PAD 的一个法向量 m ⃗⃗⃗ =（1.0.0）. 设平面PAD 与平面PBC 所成锐二面角为α. 则cosα= |m ⃗⃗⃗⃗•n ⃗⃗||m ⃗⃗⃗⃗|•|n ⃗⃗|= 4√2121. ∴平面PAD 与平面PBC 所成锐二面角的余弦值为 4√2121．【点评】：本题考查异面直线所成角的余弦值、二面角的余弦值的求法.考查空间中线线、线面、面面间的位置关系等基础知识.考查运算求解能力.是中档题．21.（问答题.0分）已知函数f（x）=lnx-ax2+2ax．（Ⅰ）若a=-1.求曲线y=f（x）在点（1.f（1））处的切线方程；（Ⅱ）若f（x）≤x恒成立.求实数a的取值范围．【正确答案】：【解析】：（I）函数f（x）的定义域为（0.+∞）．当a=-1时.f（x）=lnx+x2-2x．利用导数的运算法则可得f′（0）.而f（1）=-1．利用点斜式即可得出．（ II）若f（x）≤x恒成立.即f（x）-x≤0恒成立．设g（x）=f（x）-x=lnx-ax2+（2a-1）．对a分类讨论.利用导数研究函数的单调性x．只要g（x）max≤0即可；g′（x）=- (2a+1)(x−1)x极值最值即可得出．【解答】：解：（I）函数f（x）的定义域为（0.+∞）．当a=-1时.f（x）=lnx+x2-2x．+2x−2 .∴ f′(x)=1xf′（0）=1.且f（1）=-1．所以曲线y=f（x）在点（1.f（1））处的切线方程为y-（-1）=x-1.即x-y-2=0．（ II）若f（x）≤x恒成立.即f（x）-x≤0恒成立．设g （x ）=f （x ）-x=lnx-ax 2+（2a-1）x ．只要g （x ）max ≤0即可； g′（x ）=−2ax 2+(2a−1)x+1x =- (2a+1)(x−1)x． ① 当a=0时.令g′（x ）=0.得x=1． x.g′（x ）.g （x ）变化情况如下表：max ② 当a ＞0时.令g′（x ）=0.得x=- 12a （舍）.或x=1； x.g′（x ）.g （x ）变化情况如下表：max ③ 当a ＜0时.存在 x =2−1a ＞1 .满足g （2- 1a ）=ln （2- 1a ）＞0.所以f （x ）＜0不能恒成立.所以a ＜0不满足题意． 综上.实数a 的取值范围为[0.1]．【点评】：本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法、分类讨论方法.考查了推理能力与计算能力.属于难题．22.（问答题.0分）已知函数f （x ）=（3-x ）e x .g （x ）=x+a （a∈R ）（e 是自然对数的底数.e≈2.718…）．（1）求函数f （x ）的极值；（2）若函数y=f （x ）g （x ）在区间[1.2]上单调递增.求a 的取值范围； （3）若函数h （x ）=f (x )+g (x )x在区间（0.+∞）上既存在极大值又存在极小值.并且h （x ）的极大值小于整数b.求b 的最小值．【正确答案】：【解析】：（1）求出函数的导数.解各有导函数的不等式.求出函数的单调区间.求出函数的极值即可；（2）求出函数的导数.结合二次函数的性质得到关于a 的不等式组.解出即可；（3）求出h （x ）的导数.问题转化为r （x ）在（0.+∞）上有2个不相等的实数根x 1.x 2（x 1＜x 2）.根据r （x ）的单调性求出-3＜a ＜-e.根据h （x 2）= e x 2 （2-x 2）+1.求出函数的导数.结合函数的单调性确定b 的最小值即可．【解答】：解：（1）f′（x ）=（2-x ）e x . 令f′（x ）＞0.解得：x ＜2. 令f′（x ）＜0.解得：x ＞2.故f （x ）在（-∞.2）递增.在（2.+∞）递减. 故f （x ）极大值=f （2）=e 2.无极小值； （2）由y=f （x ）g （x ）=（3-x ）（x+a ）e x . y′=e x [-x 2+（1-a ）x+2a+3]. 令m （x ）=-x 2+（1-a ）x+2a+3.函数y=f （x ）g （x ）在区间[1.2]上单调递增 等价于对任意x∈[1.2].m （x ）≥0恒成立. ∴ {m (1)≥0m (2)≥0 .解得：a≥-3； （3）h （x ）=(3−x)e x +x+ax .h′（x ）= e x (−x 2+3x−3)−a x 2. 令r （x ）=e x （-x 2+3x-3）-a.若函数h （x ）在区间（0.+∞）上既存在极大值又存在极小值. 则h′（x ）=0在（0.+∞）上有2个不相等的实数根.即r （x ）在（0.+∞）上有2个不相等的实数根x 1.x 2（x 1＜x 2）. r′（x ）=x （1-x ）e x .故r （x ）在（0.1）递增.在（1.+∞）递减. 则0＜x 1＜1. {r (0)＜0r (1)＞0.解得：-3＜a ＜-e.故r （ 32）＜0.∵r （x ）在（0.+∞）连续且r （0）r （1）＜0.r （1）r （ 32）＜0. ∴r （x ）=0在（0.1）和（1. 32）上各有1个实根.故函数h （x ）在（0.+∞）既存在极大值又存在极小值时.有-3＜a ＜-e. 并且在区间（0.1）上存在极小值f （x 1）.在区间（1. 32 ）上存在极大值f （x 2）. 故h （x 2）=(3−x 2)e x 2+x 2+ax 2.且h′（x 2）=e x 2(−x 22+3x 2−3)−ax 22=0.故a= e x 2 （- x 22 +3x 2-3）.h（x2）= (3−x2)e x2+x2+e x2(−x22+3x2−3)x2= e x2（2-x2）+1. 令H（x）=e x（2-x）.H′（x）=e x（1-x）.故H（x）在（1.+∞）递减.∵x2∈（1. 32）.∴h（32）＜h（x2）＜h（1）.即h（x2）∈（12e32 +1.e+1）.则3＜12e32 +1＜e+1＜4.∵h（x）的极大值小于整数b.∴满足题意的整数b的最小值是4．【点评】：本题考查了函数的单调性.极值.最值问题.考查导数的应用以及转化思想.是一道综合题．。

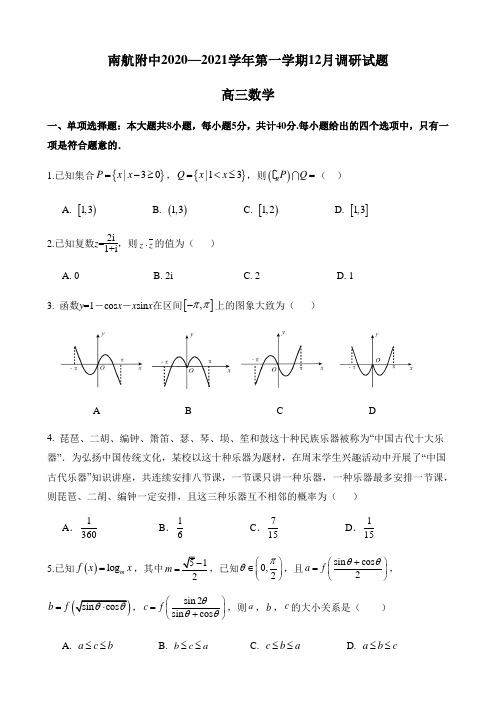
南航附中2020—2021学年第一学期12月调研试题高三数学一、单项选择题：本大题共8小题，每小题5分，共计40分.每小题给出的四个选项中，只有一项是符合题意的．1.已知集合{}30|P x x =-≥，{}13|Q x x =<≤，则()R P Q =（ ）A. [)1,3B. ()1,3C. [)1,2D. []1,3 2.已知复数z =2i1+i ，则z z ⋅的值为（ ）A. 0B. 2iC. 2D. 13. 函数y =1－cos x －x sin x 在区间上的图象大致为（ ）A B C D4. 琵琶、二胡、编钟、箫笛、瑟、琴、埙、笙和鼓这十种民族乐器被称为“中国古代十大乐器”．为弘扬中国传统文化，某校以这十种乐器为题材，在周末学生兴趣活动中开展了“中国古代乐器”知识讲座，共连续安排八节课，一节课只讲一种乐器，一种乐器最多安排一节课，则琵琶、二胡、编钟一定安排，且这三种乐器互不相邻的概率为（ ）A ．1360 B ．16 C ．715 D ．1155.已知()log m f x x =，其中m =，已知0,2πθ⎛⎫∈ ⎪⎝⎭，且sin cos 2a f θθ+⎛⎫=⎪⎝⎭，b f=，sin 2sin cos c f θθθ⎛⎫= ⎪+⎝⎭，则a ，b ，c 的大小关系是（ ）A. a c b ≤≤B. b c a ≤≤C. c b a ≤≤D. a b c ≤≤[],ππ-6.若1nx ⎫⎪⎭的展开式中二项式系数和为256，则二项式展开式中有理项系数之和为（ ） A. 85B. 84C. 57D. 567.渔民出海打鱼，为了保证获得的鱼新鲜，鱼被打上船后，要在最短的时间内将其分拣、冷藏，若不及时处理，打上来的鱼会很快失去新鲜度.已知某种鱼失去的新鲜度h 与其出水后时间t （分）满足的函数关系式为t h m a =⋅．若出水后10分钟，这种鱼失去的新鲜度为10%，出水后20分钟，这种鱼失去的新鲜度为20%．那么若不及时处理，打上来的这种鱼在多长时间后开始失去全部新鲜度（已知lg 20.3≈，结果取整数）（ ）A. 43分钟B. 45分钟C. 50分钟D. 56分钟8.已知双曲线()0,01:2222>>=-b a by a x C 的右焦点为F ，关于原点对称的两点B A 、分别在双曲线的左、右两支上，==⋅3,0且点C 在双曲线上，则双曲线的离心率为（）A ．2B ．210C ．3D ．2二、多项选择题：本大题共4小题，每小题5分，共计20分.每小题给出的四个选项中，有多个选项符合题意．全部选对的得5分，部分选对的得3分，有选错的得0分． 9．“不等式x 2－2x +m >0在x ∈R 上恒成立”的一个充分不必要条件是（ ）A. m >1B. 0<m <2C. m > 2D. m >310．已知数列{}n a 为等差数列，其前n 项和为n S ，若13 *(n n S S n N -=∈且13)n <，则正确的结论为（ ）A. {}n a 为递增数列B. 70a =C. 130S =D.130a = 11．已知函数()f x 的定义域为R ，且对任意x ∈R 都满足()()11f x f x +=-，当1x ≤时，()ln ,01e ,0xx x f x x <≤⎧=⎨≤⎩(其中e 为自然对数的底数，)若函数()2g x m x =-与()y f x =的图像恰有两个交点，则实数m 的取值可以是（ ）A. e - B ． 0 C ． e D ．e 212．在直角梯形ABCD 中，π2ABC BCD ∠=∠=，E DC BC AB ,2,1===为DC 中点，现将△ADE 沿AE 折起，得到一个四棱锥ABCE D -,则下列命题正确的有（ ）A ．在△ADE 沿AE 折起的过程中，四棱锥ABCE D -体积的最大值为31B ．在△ADE 沿AE 折起的过程中，异面直线AD 与BC 所成的角恒为4πC ．在△ADE 沿AE 折起的过程中，二面角D EC A --的大小为 45D ．在四棱锥ABCE D -中，当D 在EC 上的射影恰好为EC 的中点F 时,DB 与平面ABCE 所成的角的正切为515三､填空题：本大题共4小题，每小题5分，共20分13.若函数()sin 3cos f x x x ωω=+ (x ∈R ，0>ω)满足()()02f f αβ==，，且||αβ-的最小值等于2π，则ω的值为___________. 14.已知直线:1l x y -=与圆22:2210M x y x y +-+-=相交于,A C 两点，点,B D 分别在圆M 上运动，且位于直线AC 两侧，则四边形ABCD 面积的最大值为_______________. 15.如图，已知两座建筑物,AB CD 的高度分别为15m 和9m ，且AB BC CD >>，从建筑物AB 的顶部A 看建筑物CD 的张角为CAD ∠，测得6tan 13CAD ∠=，则,B C 间的距离_______m .16.已知点O ,A ,B ,C 在同一平面，且A ,B ,C 三点不共线，且满足OA OB OC ++=0,其中||6,||2,||14OA OB OC ===,则OA OB ⋅的值为 ，则△ABC 的面积为 ．(第一空2分，第二空3分)四､解答题：本大题共6小题，共70分解答应写出文字说明､证明过程或演算步骤． 17. 在 ①cosB=－23； ②a =7； ③b =3 这三个条件中选取两个补充在下面问题中，使得问题中的三角形存在，并说明理由.问题：在△ABC 中，a ，b ，c 是角A ，B ，C 所对的边，已知sinB －sinC=sin(A －C)， 且________和_________(填写条件序号) ，求△ABC 的面积.18.已知数列{a n }是等差数列，a 2=3，且a 32=2a 7. （1）求数列{a n }的通项公式；（2）若a 1>0，设数列{b n }满足2b 1+22b 2+23b 3+24b 4+… … +2n b n =a n . n ∈N *，求数列{b n }的前n 项和T n19.如图,在直棱柱111C B A ABC -中,BC AB =,111C A AC AA 、、的中点分别为F E D 、、. （1）求证:⊥AC 平面BEF ;（2）若异面直线1AA 与BF 所成的角为 45，且BC 与平面BEF 所成角的正弦值为55,求二面角1B CD B --的余弦值.D1AA20.蚂蚁森林是支付宝推出的公益活动，用户可以通过步行、在线缴费等减排行为获得积分，参与在荒漠化地区种树，该公益活动曾获得联合国“地球卫士奖”．蚂蚁森林2016年8月在支付宝上线，截止2020年8月5.5亿蚂蚁森林用户一起累计种下超过2.2亿颗真树．用户通过蚂蚁森林一年种植3棵树，可获得当年度全民义务植树尽责证书．某高校学生会调查了该校100名学生通过蚂蚁森林获得2020年度全民义务植树尽责证书的情况，已知这100名学生中有男生70名，男生中通过蚂蚁森林获得2020年度全民义务植树尽责证书人数占男生总数的67，女生中通过蚂蚁森林获得2020年度全民义务植树尽责证书人数占女生总数的23．（1）填写下列2×2列联表，并判断是否有95%的把握认为该校学生的性别与通过蚂蚁森林获得2020年度全民义务植树尽责证书有关系？（2）若把这100名学生通过蚂蚁森林获得2020年度全民义务植树尽责证书的频率作为该校每个学生通过蚂蚁森林获得2020年度全民义务植树尽责证书的概率，从全校所有学生中随机取出4个人，记这4人中通过蚂蚁森林获得2020年度全民义务植树尽责证书的人数与未通过蚂蚁森林获得2020年度全民义务植树尽责证书的人数之差为X，求X的分布列与期望．附：n＝a+b+c+d，22()()()()()n ad bcKa b c d a c b d-=++++．21.椭圆()01:2222>>=+b a b y a x C 的离心率为21，其右准线方程为4=x ，A 、B 分别为椭圆的左、右顶点，过点B A 、作斜率分别为21k k 、直线AM 和直线BN 分别与椭圆C 交于点N M ,（其中M 在x 轴上方，N 在x 轴下方）.(1)求椭圆C 的方程;(2)若直线MN 恒过椭圆的左焦点1F ,求证:21k k为定值.22．设函数()(1)ln(1)f x ax x bx =+++．（1）若1b =-，求曲线()y f x =在坐标原点处的切线方程； （2）当1a =时，讨论函数()f x 在[0,)+∞上的极值点的个数； （3）证明：*2ln 3ln 4ln(1)ln 2()491n nn N n n ++++⋯+>∈+.南航附中2020—2021学年第一学期12月调研试题高三数学一、单项选择题：本大题共8小题，每小题5分，共计40分.每小题给出的四个选项中，只有一项是符合题意的．1.已知集合{}30|P x x =-≥，{}13|Q x x =<≤，则()R P Q =（ ）BA. [)1,3B. ()1,3C. [)1,2D. []1,3 2.已知复数z =2i1+i ，则z z ⋅的值为（ ）CA. 0B. 2iC. 2D. 13. 函数y =1－cos x －x sin x 在区间上的图象大致为（ ）D[],ππ-A B C D4. 琵琶、二胡、编钟、箫笛、瑟、琴、埙、笙和鼓这十种民族乐器被称为“中国古代十大乐器”．为弘扬中国传统文化，某校以这十种乐器为题材，在周末学生兴趣活动中开展了“中国古代乐器”知识讲座，共连续安排八节课，一节课只讲一种乐器，一种乐器最多安排一节课，则琵琶、二胡、编钟一定安排，且这三种乐器互不相邻的概率为（ ）BA ．1360 B ．16 C ．715 D ．1155.已知()log m f x x =，其中12m =，已知0,2πθ⎛⎫∈ ⎪⎝⎭，且sin cos 2a f θθ+⎛⎫=⎪⎝⎭，b f=，sin 2sin cos c f θθθ⎛⎫= ⎪+⎝⎭，则a ，b ，c 的大小关系是（ ）DA. a c b ≤≤B. b c a ≤≤C. c b a ≤≤D. a b c ≤≤6.若1nx ⎫⎪⎭的展开式中二项式系数和为256，则二项式展开式中有理项系数之和为（ ）AA. 85B. 84C. 57D. 567.渔民出海打鱼，为了保证获得的鱼新鲜，鱼被打上船后，要在最短的时间内将其分拣、冷藏，若不及时处理，打上来的鱼会很快失去新鲜度.已知某种鱼失去的新鲜度h 与其出水后时间t （分）满足的函数关系式为t h m a =⋅．若出水后10分钟，这种鱼失去的新鲜度为10%，出水后20分钟，这种鱼失去的新鲜度为20%．那么若不及时处理，打上来的这种鱼在多长时间后开始失去全部新鲜度（已知lg 20.3≈，结果取整数）（ ）AA. 43分钟B. 45分钟C. 50分钟D. 56分钟8.已知双曲线()0,01:2222>>=-b a by a x C 的右焦点为F ，关于原点对称的两点B A 、分别在双曲线的左、右两支上，FC BF FB AF ==⋅3,0且点C 在双曲线上，则双曲线的离心率为（）BA ．2B ．210 C ．3 D ．2二、多项选择题：本大题共4小题，每小题5分，共计20分.每小题给出的四个选项中，有多个选项符合题意．全部选对的得5分，部分选对的得3分，有选错的得0分． 9．“不等式x 2－2x +m >0在x ∈R 上恒成立”的一个充分不必要条件是（ ）CDA. m >1B. 0<m <2C. m > 2D. m >310．已知数列{}n a 为等差数列，其前n 项和为n S ，若13 *(n n S S n N -=∈且13)n <，则正确的结论为（ ）BCA. {}n a 为递增数列B. 70a =C. 130S =D.130a = 11．已知函数()f x 的定义域为R ，且对任意x ∈R 都满足()()11f x f x +=-，当1x ≤时，()ln ,01e ,0xx x f x x <≤⎧=⎨≤⎩(其中e 为自然对数的底数，)若函数()2g x m x =-与()y f x =的图像恰有两个交点，则实数m 的取值可以是（ ）ABCA. B ． 0 C ． e D ．e 212．在直角梯形ABCD 中，π2ABC BCD ∠=∠=，E DC BC AB ,2,1===为DC 中点，现将△ADE 沿AE 折起，得到一个四棱锥ABCE D -,则下列命题正确的有（ ）ABDA ．在△ADE 沿AE 折起的过程中，四棱锥ABCE D -体积的最大值为31B ．在△ADE 沿AE 折起的过程中，异面直线AD 与BC 所成的角恒为4πC ．在△ADE 沿AE 折起的过程中，二面角D EC A --的大小为 45D ．在四棱锥ABCE D -中，当D 在EC 上的射影恰好为EC 的中点F 时,DB 与平面ABCE所成的角的正切为515 三､填空题：本大题共4小题，每小题5分，共20分13.若函数()sin 3cos f x x x ωω=+ (x ∈R ，0>ω)满足()()02f f αβ==，，且||αβ-的最小值等于2π，则ω的值为___________. 1 14.已知直线:1l x y -=与圆22:2210M x y x y +-+-=相交于,A C 两点，点,B D 分别在圆M 上运动，且位于直线AC 两侧，则四边形ABCD 面积的最大值为_______________. 30 15.如图，已知两座建筑物,AB CD 的高度分别为15m 和9m ，且AB BC CD >>，从建筑物AB 的顶部A 看建筑物CD 的张角为CAD ∠，测得6tan 13CAD ∠=，则,B C 间的距离_______m . 1216.已知点O ,A ,B ,C 在同一平面，且A ,B ,C 三点不共线，且满足OA OB OC ++=0,其中||6,||2,||14OA OB OC ===,则OA OB ⋅的值为 ，则△ABC 的面积为 ．(第一空2分，第二空3分) 2，35四､解答题：本大题共6小题，共70分解答应写出文字说明､证明过程或演算步骤． 17. 在 ①cosB=－23； ②a =7； ③b =3 这三个条件中选取两个补充在下面问题中，使得问题中的三角形存在，并说明理由.问题：在△ABC 中，a ，b ，c 是角A ，B ，C 所对的边，已知sinB －sinC=sin(A －C)， 且________和_________(填写条件序号) ，求△ABC 的面积.18.已知数列{a n}是等差数列，a2=3，且a32=2a7.（1）求数列{a n}的通项公式；（2）若a1>0，设数列{b n}满足2b1+22b2+23b3+24b4+…… +2n b n=a n. n∈N*，求数列{b n}的前n项和T n19.如图,在直棱柱111C B A ABC -中,BC AB =,111C A AC AA 、、的中点分别为F E D 、、.（1）求证:⊥AC 平面BEF ;（2）若异面直线1AA 与BF 所成的角为 45，且BC 与平面BEF 所成角的正弦值为55,求二面角1B CD B --的余弦值.（1）证明：在ABC ∆中，BC AB = ，∴AC BE ⊥，在直棱柱111C B A ABC -中， 四边形11ACC A 是平行四边形，∴11//AC AC =又 F 是11C A 的中点，E 是AC 的中点，∴AE F A =//1， ∴四边形AEF A 1是平行四边形∴EF A A //1, 在直棱柱111C B A ABC -中，∴ABC A A 平面⊥1 ABC AC 平面⊂，∴AC A A ⊥1,∴AC EF ⊥,又 AC BE ⊥，E BE EF =⋂，BEF ,平面⊂BE EF ,∴⊥AC 平面BEF （6分）（2）解：以E 为原点，EF EC EB ,,所在直线分别为z y x ,,轴，建立空间直角坐标系.由题知,55sin ,45=∠=∠CBE BEF ,设,1=BE 则1=EF , 由(1)知,AC BE ⊥,∴ 90=∠BEC ,∴在BEC Rt ∆中，CBE ∠为锐角又 55sin =∠CBE ，∴552sin 1cos 2=∠-=∠CBE CBE ，∴21tan =∠CBE ，∴21=BE EC ，∴21=EC ,从而，)21,21,0(),0,21,0(),1,0,1(),0,0,1(1-D C B B ∴)1,21,1(),0,21,1(),21,1,0(1-=-=-=CBD1A A设平面BCD 的一个法向量为),,(z y x =，则⎪⎩⎪⎨⎧=⋅=⋅00CD m ，⎪⎪⎩⎪⎪⎨⎧=-=+-∴021021y x z y ，取2=y ，得4,1==z x ，∴)4,2,1(=. 设平面BCD 的一个法向量为),,(c b a =，则⎪⎩⎪⎨⎧=⋅=⋅001CB ,⎪⎪⎩⎪⎪⎨⎧=+-=+-∴021021c b a c b , 取2=c ,得1,3=-=b a ,∴)2,1,3(-=n .设二面角1B CD B --的平面角为θ,则661421823cos =⨯++-==θ （12分） 20.蚂蚁森林是支付宝推出的公益活动，用户可以通过步行、在线缴费等减排行为获得积分，参与在荒漠化地区种树，该公益活动曾获得联合国“地球卫士奖”．蚂蚁森林2016年8月在支付宝上线，截止2020年8月5.5亿蚂蚁森林用户一起累计种下超过2.2亿颗真树．用户通过蚂蚁森林一年种植3棵树，可获得当年度全民义务植树尽责证书．某高校学生会调查了该校100名学生通过蚂蚁森林获得2020年度全民义务植树尽责证书的情况，已知这100名学生中有男生70名，男生中通过蚂蚁森林获得2020年度全民义务植树尽责证书人数占男生总数的67，女生中通过蚂蚁森林获得2020年度全民义务植树尽责证书人数占女生总数的23．（1）填写下列2×2列联表，并判断是否有95%的把握认为该校学生的性别与通过蚂蚁森林获得2020年度全民义务植树尽责证书有关系？（2）若把这100名学生通过蚂蚁森林获得2020年度全民义务植树尽责证书的频率作为该校每个学生通过蚂蚁森林获得2020年度全民义务植树尽责证书的概率，从全校所有学生中随机取出4个人，记这4人中通过蚂蚁森林获得2020年度全民义务植树尽责证书的人数与未通过蚂蚁森林获得2020年度全民义务植树尽责证书的人数之差为X ，求X 的分布列与期望．附：P(K2≥k0) 0.05 0.01 0.005 0.001k0 3.841 6.635 7.879 10.828n＝a+b+c+d，22()()()()()n ad bcKa b c d a c b d-=++++．21.椭圆()01:2222>>=+b a b y a x C 的离心率为21，其右准线方程为4=x ，A 、B 分别为椭圆的左、右顶点，过点B A 、作斜率分别为21k k 、直线AM 和直线BN 分别与椭圆C 交于点N M ,（其中M 在x 轴上方，N 在x 轴下方）. (1)求椭圆C 的方程;(2)若直线MN 恒过椭圆的左焦点1F ,求证:21k k 为定值. 解:(1) 如图所示，设焦距为2c(c>0),⎩⎨⎧==⇒⎪⎪⎩⎪⎪⎨⎧==124212c a ca a c , ∴3=b , ∴13422=+y x （4分） (2) 设12)2(43134)2(:212221=++⇒⎪⎩⎪⎨⎧=++=x k x y x x k y AM ∴0121616)34(2121221=-+++k x k x k ,34121622121+-=-k k x M ,34862121+-=k k x M )23486()2(212111++-=+=k k k x k y M =3412211+k k34682222+-=k k x N ,3412222+-=k k y N∵MN 过左焦点1F ,∴11NF MF k k =,∴13468341213486341222222222121211++-+-=++-+k k k k k k k k ,312124912222211--=-k k k k22113121941k k k k -=-,∴21122121)3(339124k k k k k k k k -=-=-, ∴124120k k -=或4321-=k k （舍）,∴123k k =. （12分）22．设函数()(1)ln(1)f x ax x bx =+++．（1）若1b =-，求曲线()y f x =在坐标原点处的切线方程； （2）当1a =时，讨论函数()f x 在[0,)+∞上的极值点的个数； （3）证明：*2ln 3ln 4ln(1)ln 2()491n nn N n n ++++⋯+>∈+. 【详解】解：（1）当1b =-时，()(1)ln(1)f x ax x x =++-，1()ln(1)11ax f x a x x +'=++-+， ()00f ∴=，()00f '=，即曲线()y f x =在坐标原点处的切线方程为0y =； （3分） （2）当1a =时，()()()1ln 1f x x x bx =+++，()()ln 11f x x b '=+++， 令()0f x '=，则11b x e --=-，当1b ≥-时，0x ≥时，()0f x '≥，()f x 在[0,)+∞上单调递增，()f x ∴在[0,)+∞上没有极值点；当1b <-时，当101b x e --≤<-时，()0f x '<，()f x 单调递减，当11b x e -->-时，()0f x '>，()f x 单调递增，11b x e --∴=-是()f x 的极小值点， 综上，1b ≥-时，()f x 在[0,)+∞上没有极值点；1b <-时，()f x 在[0,)+∞上只有一个极小值点11b x e --=-，没有极大值点； （7分）（3）取1a =，1b =-，由（2）知()f x 在(0,)+∞上单调递增，0x ∴>时，()0f x >，∴当n *∈N 时，()0f n >，即(1)ln(1)0n n n ++->，即2ln(1)1(1)n n n n +>+， 1ln 212>⨯，ln 31423>⨯，ln 41934>⨯，…，2ln(1)1(1)n n n n +>+， 将上面不等式相加得：2ln 3ln 4ln(1)1111ln 249122334(1)n n n n +++++>++++⨯⨯⨯+，又1111223(1)n n +++⨯⨯+11111111223341n n ⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭111n =-+ 1n n =+， 2ln 3ln 4ln(1)ln 2491n nn n +∴++++>+. （12分）。

南京市2020～2021学年度第一学期期中调研模拟卷高 二 数 学 2020.10一、单选题（本大题共8小题，每小题 4分，共32分）1．已知(cos ,sin )P αα，(cos ,sin )Q ββ，则||PQ 的最大值为（ ▲ ）A B ．2C ．4D ．2．若△ABC 中，2sin()sin()sin A B A B C +-=，则此三角形的形状是（ ▲ ）A ．直角三角形B ．等腰三角形C ．等边三角形D ．等腰直角三角形3．设m ，n 是不同的直线，α，β，γ是三个不同的平面，有以下四个命题： ①若m α⊥，n β⊥，则//m n ； ②若m αγ=，n βγ=，//m n ，则//αβ；③若γα⊥，γβ⊥，则//αβ．④若//αβ，//βγ，m α⊥，则m γ⊥；其中正确命题的序号是（ ▲ ） A ．①③B ．②③C ．③④D ．①④4．已知双曲线C ：22221x y a b-=（0a >，0b >），过C 的右焦点F 作垂直于渐近线的直线l 交两渐近线于A ，B 两点，A ，B 两点分别在一、四象限，若513AF BF =，则双曲线C 的离心率为（ ▲ ）A ．1312B C D 5．已知直线0(0)x y a a +-=>与圆224x y +=交于不同的两点,,A B O 是坐标原点，且有||||OA OB AB +≥，那么a 的取值范围是（ ▲ ）A ．)+∞B ．(2,)+∞C ．[2,D ．6．在菱形ABCD 中，4,60AB A ︒=∠=，将ABD △沿对角线BD 折起使得二面角A BD C --的大小为60°，则折叠后所得四面体ABCD 的外接球的半径为（ ▲ ）A ．3B ．3C ．3D ．37．已知点G 是ABC ∆的重心，(,)AG AB AC R λμλμ=+∈，若120A ∠=，2AB AC ⋅=-，则AG 的最小值是（ ▲ ）A B ．2C ．23D ．348．过抛物线216y x =焦点F 的直线l 与抛物线相交于A ，B 两点，若以线段AB 为直径的圆与直线13x =相切，则直线l 的方程为（ ▲ ）A ．y =-y =-+B ．416y x =-或416y x =-+C ．28y x =-或28y x =-+D ．4y x =-或4y x =-+二、多选题（本大题共4 小题，每小题5分，共 20 分） 9．已知2sin 3θ=-，且cos 0θ>，则（ ▲ ） A ．tan 0θ< B ．24tan9θ>C ．22sin cos θθ>D ．sin20θ>10．如图所示，某探月卫星沿地月转移轨道飞向月球，在月球附近一点P 变轨进入以月球球心F 为一个焦点的椭圆轨道I 绕月飞行，之后卫星在点P 第二次变轨进入仍以F 为一个焦点的椭圆轨道II 绕月飞行，最终卫星在点P 第三次变轨进入以F 为圆心的圆形轨道III 绕月飞行，若用12c 和22c 分别表示椭圆轨道I 和II 的焦距，用12a 和22a 分别表示椭圆轨道I 和II 的长轴长，则下列式子正确的是（ ▲ ）A ．1122a c a c +=+B ．1122a c a c -=-C ．1212c a a c >D ．1212c c a a <11．如图，在四棱锥E ABCD -中，底面ABCD 是边长为2的正方形，CDE △是正三角形，M 为线段DE 的中点，点N 为底面ABCD 内的动点，则下列结论正确的是（ ▲ ） A ．若BC DE ⊥，则平面CDE ⊥平面ABCDB ．若BC DE ⊥，则直线EA 与平面ABCD 所成的角的正弦值为64C ．若直线BM 和EN 异面，则点N 不可能为底面ABCD 的中心D ．若平面CDE ⊥平面ABCD ，且点N 为底面ABCD 的中心，则BM EN =12．泰戈尔说过一句话：世界上最远的距离，不是树枝无法相依，而是相互了望的星星，却没有交会的轨迹；世界上最远的距离，不是星星之间的轨迹，而是纵然轨迹交会，却在转瞬间无处寻觅．已知点()10M ，，直线l ：2x =-，若某直线上存在点P ，使得点P 到点M 的距离比到直线l 的距离小1，则称该直线为“最远距离直线”，则下列结论正确的是（ ▲ ） A ．点P 的轨迹曲线是一条线段B ．点P 的轨迹与直线'l ：1x =-是没有交会的轨迹(即两个轨迹没有交点)C ．26y x =+不是“最远距离直线”D ．112y x =+是“最远距离直线” 三、填空题（本大题共4 小题，每小题5分，共 20 分）13．已知在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且2cos A sin B =sin A +2sin C ．则B =▲ .14．已知圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为78，SA 与圆锥底面所成角为45°，若SAB 的面积为515，则该圆锥的侧面积为 ▲ ．15．阿波罗尼斯（古希腊数学家，约公元前262-190年）的著作《圆锥曲线论》是古代世界光辉的科学成果，它将圆锥曲线的性质网罗殆尽几乎使后人没有插足的余地.他证明过这样一个命题：平面内与两定点距离的比为常数k （0k >且1k ≠）的点的轨迹是圆，后人将这个圆称为阿氏圆现有ABC ，6AC =，sin 2sin C A =，则当ABC 的面积最大时，它的内切圆的半径为 ▲ .16．已知抛物线()2:20C x py p =>的焦点为F ，直线():0l y kx b k =+≠与抛物线C 交于A ，B两点，且6AF BF +=，线段AB 的垂直平分线过点()0,4M ，则抛物线C 的方程是 ▲ ；若直线l 过点F ，则k = ▲ . 四、解答题（本大题共6 小题，共 78 分）17．（10分）在ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，并且222b c a bc +-=.已知 ▲ ，计算ABC 的面积.请①7a =，②2b =，③sin 2sin C B =这三个条件中任选两个，将问题（1）补充完整，并作答.注意，只需选择其中的一种情况作答即可.18．（12分）如图，在平面直角坐标系xOy 中，角θ的终边与单位圆交于点P . （1）若点P 的横坐标为35，求cos2sin cos θθθ-⋅的值.（2）若将OP 绕点O 逆时针旋转4π，得到角α(即4παθ=+)，若1tan 2α=，求tan θ的值.19．（12分）在平面直角坐标系xOy 中，点(),P x y 为动点，已知点()2,0A，()2,0B -，直线PA 与PB 的斜率之积为定值12-． （1）求动点P 的轨迹E 的方程；（2）若()1,0F ，过点F 的直线l 交轨迹E 于M 、N 两点，以MN 为对角线的正方形的第三个顶点恰在y 轴上，求直线l 的方程．20．（14分）如图所示，该几何体是由一个直三棱柱ADE BCF 和一个正四棱锥P ABCD -组合而成，AD AF ⊥，2AE AD ==． （Ⅰ）证明：平面PAD ⊥平面ABFE ；（Ⅱ）求正四棱锥P ABCD -的高h ，使得二面角C AF P --的余弦值是22．21．（14分）已知点P 是抛物线21:4C y x =的准线上任意一点，过点P 作抛物线1C 的两条切线PA 、PB ，其中A 、B 为切点.（1）证明：直线AB 过定点，并求出定点的坐标；（2）若直线AB 交椭圆222:143x y C +=于C 、D 两点，1S 、2S 分别是PAB △、PCD 的面积，求12S S 的最小值.22．（16分）已知圆C 的圆心在直线30x y -=上，与x 轴正半轴相切，且被直线l ：0x y -=截得的弦长为27. （1）求圆C 的方程；（2）设点A 在圆C 上运动，点()7,6B ，且点M 满足2AM MB =，记点M 的轨迹为Γ. ①求Γ的方程，并说明Γ是什么图形；②试探究：在直线l 上是否存在定点T (异于原点O )，使得对于Γ上任意一点P ，都有PO PT为一常数，若存在，求出所有满足条件的点T 的坐标，若不存在，说明理由.参考答案1．B2．A 3．D 4．B 5．C 6．A 7．C 8．B 9．AB 10．BC 11．ABC 12．BCD 13．23π14．15116．24x y = ±17．答案不唯一，见解析 18．（1）15（2）13-19．（1）()22102x y y +=≠；（2）10x y --=或10x y +-=． 20．（Ⅰ）见解析;（Ⅱ）1h =．21．（1）定点坐标为()1,0，证明见解析；（2）43. 22．（1）()()22139x y -+-=；（2）①()()22551x y -+-=，Γ是圆；②存在， 4949,1010D ⎛⎫⎪⎝⎭.。

南京市2020-2021学年第一学期期中调研测试高二数学一、单项选择题:本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．在平面直角坐标系xoy 中，已知抛物线x 2=2y 的焦点为F ，准线为l ,则点F 到准线l 的距离为（ ）A ．12B. 1C. 2D. 4 2. 已知向量a →=（-2，3，-1），b →=（4，m ，n ），且 a →||b →，其中m,n ∈R,则m+n=( )A ．4 B. -4 C. 2 D. —23．若sinθ=2cos(π-θ),则t an(θ+π4)的值为（ ） A ．3 B. 13 C. —3 D. — 134.在平面直角坐标系xoy 中，若椭圆C ：x 29 + y 2m =1 与双曲线T ：x 2— y 2m=1 有相同的焦点，则双曲线T 的渐近线方程为（ ）A. y= ±14 xB. y= ±12x C . y= ±4x D . y= ±2x 5. 在平面直角坐标系xoy 中，直线x+2y-4=0与两坐标轴分别交于点A ，B ，圆C 经过A ，B ，且圆心在y 轴上，则圆C 的方程为（ ）A. x 2+y 2+6y-16=0B. x 2+y 2-6y-16=0C. x 2+y 2+8y-9=0 D .x 2+y 2-8y-9=06.如图，已知圆柱的底面半径为2，与圆柱底面成600角的平面截这个圆柱得到一个椭圆，则该椭圆的焦距为（ ）A ．2 2 B. 2 3 C. 4 2 D. 4 37．如图，在三棱柱ABC-A 1B 1C 1中，BC 1与B 1C 相交于点O ，∠A 1AB=∠A 1AC=600，∠BAC=900，A 1A=3，AB=AC=2，则线段AO 的长度为（ ） A.29 2 B.29 C. 23 2D. 23 8. 在平面直角坐标系xoy 中，已知双曲线C ：x 2a 2 - y 2b2 =1 (a>0,b>0)的左焦点为F ，点M ，N 在双曲线C 上，若四边形OFMN 为菱形，则双曲线C 的离心率为（ ）A ． 3 -1．B. 5 -1 C. 3 +1 D. . 5 +1二、多项选择题:本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得5分，部分选对的得3分，不选或有选错的得0分.9．已知两个不重合的平面α,β及直线m,下列说法正确的是（ ）A ．若α⊥β，m ⊥α, 则m ||β B. 若α||β，m ⊥α, 则m ⊥βC. 若m||α，m ⊥β, 则α⊥βD. 若m||α，m||β, 则α||β10. 在平面直角坐标系xoy 中，F 1，F 2分别为椭圆 x 24 + y 22=1 的左、右焦点，点A 在椭圆上.若△AF 1F 2为直角三角形，则AF 1的长度可以为（ ）A ．1B ．2C ．3D ．411．如图，直线21,l l 相交于点O ，点P 是平面内的任意一点，若x,y 分别表示点P 到21,l l 的距离，则称（x,y ）为点P 的“距离坐标”.下列说法正确的是（ ）A ．距离坐标为（0，0）的点有1个B ．距离坐标为（0，1）的点有2个C ．距离坐标为（1，2）的点有4个D ．距离坐标为（x ，x ）的点在一条直线上12．20世纪50年代，人们发现利用静态超高压和高温技术，通过石墨等碳质原料和某些金属反应可以人工合成金刚石，人工合成金刚石的典型晶态为立方体（六面体）、八面体和立方八面体以及他们的过渡形态. 其中立方八面体（如图所示）有24条棱、12个顶点，14个面（6个正方形、八个正三角形），它是将立方体“切”去8个“角”后得到的几何体.已知一个立方八面体的棱长为1，则（ ）A ．它的所有顶点均在同一个球面上，且该球的直径为2.B.它的任意两条不共面的棱所在的直线都互相垂直.C.它的体积为 5 2 3D. 它的任意两个共棱的面所成的二面角都相等. 三、填空题：本大题共4小题，每小题5分，共20分.13．在平面直角坐标系xoy 中，已知直线1l ：x+ay=0和直线2l :2x-(a-3)y-4=0,a ∈R,若1l 与2l 平行，则1l 与2l 之间的距离为 .14．在空间直角坐标系中，若三点A （1，-1，a ）,B(2,a,0),C(1,a,-2)满足：（AB →-2AC →）⊥BC →，则实数a 的值为 .15. 词语“堑堵”、“阳马”、“鳖臑”等出现自中国数学名著《九章算术•商功》，是古代人对一些特殊锥体的称呼.在《九章算术•商功》中，把四个面都是直角三角形的四面体称为“鳖臑”，现有如图所示的“鳖臑”四面体PABC ，其中PA ⊥平面ABC ，PA=AC=1，BC= 2 ，则四面体PABC 的外接球的表面积为 。

南航附中2023-2024学年度第一学期期中考试高三数学一､单选题（每题5分）1.已知集合，则（ ）A. B. C. D.2.若复数满足（其中是虚数单位），复数的共轭复数为，则（ ）A.的实部是B.的虚部是C.复数在复平面内对应的点在第一象限D.3.向量在向量上的投影向量为，且，则数量积（ ）A.8B.-8C.32D.164.已知，则（ ）B.D.5.三棱锥中，与均为边长为2的等边三角形，若平面平面，则该三棱锥外接球的表面积为（ ）A.B. C. D.6.已知数列为无穷项等比数列，为数列的前项和，则“且公比”是“恒成立”的（）A.必要而不充分条件B.充分而不必要条件C.充分必要条件D.既不充分也不必要条件7.已知直线与椭圆交于两点，线段的中点为，则的离心率可能是（ ）{}*24,A x x x B x y ⎧=∈==⎨⎩N ∣…A B ⋂=R ð[]0,3{}1,2,3{}1,2[]1,3z ()12i 34i z +⋅=+i z z z 115-z 25z 5z =a b 4b 2b = a b ⋅= tan 2α=-cos πcos 4αα=⎛⎫+ ⎪⎝⎭A BCD -ABD V BCD V ABD ⊥BCD 8π320π8π20π3{}n a n S {}n a n 10a >0q >0n S >13y x t =-+2222:1(0)x y C a b a b+=>>,A B AB 1,(2)2P m m ⎛⎫> ⎪⎝⎭CA. B. C. D.8.已知函数满足：，对任意恒成立.若成立，则实数的取值范围是（ ）A. B.C.D.二､多选题（每题5分，漏选得2分，错选不得分）9.下列选项中，正确的命题是（）A.已知随机变量，若，则B.的展开式中的系数为10C.用独立性检验进行检验时，的值越大，说明有更大的把握认为两事件有关系D.样本相关系数越接近1，成对样本数据的线性相关程度越弱10.将函数的图象向右平移个单位长度得到的图象，则（ ）A.在上是减函数B..C.是奇函数D.在上有4个零点11.甲､乙､丙三人玩传球游戏，第1次由甲传出，每次传球时，传球者都等可能地将球传给另外两人中的任何一人.设第次传球后球在甲手中的概率为，则下列结论正确的有（ ）A.B.C.D.⎫⎪⎪⎭⎫⎪⎪⎭⎫⎪⎪⎭⎫⎪⎪⎭()f x ()()22f x f x -+=[)()()()()12122121,1,,0x x x x f x f x x x ∞⎡⎤∈+≠-⋅->⎣⎦()()422622f x ax f x ++-…a (]{},20∞--⋃(],2∞--[)2,∞-+[)()2,00,∞-⋃+(),X B n p ~()()30,20E X D X ==13p =5122x y ⎛⎫- ⎪⎝⎭23x y 2χ2χr ()π2cos 24f x x ⎛⎫=-⎪⎝⎭π8()y g x =()y f x =ππ,42⎡⎤⎢⎥⎣⎦ππ44f x f x ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭()y g x =()1y g x =-[]π,π-k *,k p k ∈N 10p =213p =121k k p p ++=202313p >12.曲率半径是用来描述曲线上某点处曲线弯曲变化程度的量，已知对于曲线上点处的曲率半径公式为，则下列说法正确的是（ ）A.若曲线上某点处的曲率半径越大，则曲线在该点处的弯曲程度越小B.若某焦点在轴上的椭圆上一点处的曲率半径的最小值为（半焦距），则该椭圆离心率为C.椭圆上一点处的曲率半径的最大值为D.若椭圆上所有点相应的曲率半径最大值为8，最小值为1，则椭圆方程为三､填空题（每题5分）13.已知的展开式中第9项､第10项､第11项的二项式系数成等差数列，则正整数__________.14.已知的内角所对的边分别为，若，且内切圆面积为，则周长的最小值是__________.15.已知抛物线，点为直线上一动点，过点作直线与分别切于点，则__________.16.已知函数，若，则的最小值为__________.四､解答题（共70分）17.（10分）已知的前项和为是公比为的等比数列.（1）求的通项公式；（2）设，求数列的前项和.22221(0)x y a b a b+=>>()00,P x y 3222220044x y R a b a b ⎛⎫=+ ⎪⎝⎭x c 22221(0)x y a b a b +=>>2b a22221(0)x y a b a b +=>>221164x y +=(1n n =ABC V ,,A B C ,,a b c ()sin sin 2B Ca A Cb ++=ABC V 4πABC V 2:4C x y =M 1y =-M ,MA MB C ,A B MA MB ⋅=()()()()e 1,1ln xf x xg x x x =+=+()()12(1)f x g x m m ==>112ln x x x m+{}n a n 1,2,2n n n S S a a ⎧⎫=-⎨⎬⎩⎭12{}n a ()2212221log log log log n n n n n n a a b a a a +++=+⋅{}n b n n T18.（12分）记锐角的内角的对边分别为，已知.（1）求证：；（2）若，求的最大值.19.（12分）如图，在四棱锥中，侧面底面是边长为2的等边三角形，底面为直角梯形，其中.（1）求到平面的距离.（2）线段上是否存在一点，使得平面与平面？若存在，求出的值；若不存在，请说明理由.20.（12分）已知函数.（1）当时，求曲线在处的切线方程；（2）若，求的取值范围.21.（12分）数据中心是全球协作的特定设备网络，用于在网络上处理､存储和传递数据信息.由于数据中心对算力的要求很高，在高速运转时往往会产生巨大的热量.如果不对设备进行散热，会对设备的正常运作造成不可忽视的影响.氟化液是最为适合浸没式液冷系统的电子设备冷却液.由于氟化液技术壁垒较高，此前高性能电子氟化液长期被国外垄断.2020年巨化集团技术中心成功开发出高性能巨芯冷却液，填补了国内高性能大数据中心专用冷却液的空白.一工厂生产某型号的氯化液其抗张强度⩾100为合格品，否则为不合格品.该厂有新旧两套生产设备同时生产，按两设备生产量分层抽样进行检测，其中新设备和旧设备生产的产品中分别抽取了12桶和8桶，测得每桶抗张强度值（单位：）如下表所示：甲102.1101.0100.8103.6107.699.9100.2100.9105.798.8103.2104.1乙103.3102.6107.199.5102.8103.699.5102.3（1）根据抽检结果请完成下面的列联表，试根据小概率值的独立性检验，分析新设备是否比旧设备好.ABC V ,,A B C ,,a b c ()()sin sin cos cos A B A C BC--=B C =sin 2a C =2211a b+P ABCD -PAD ⊥,ABCD PAD V ABCD BC ∥,,1AD AB AD AB BC ⊥==B PCD PD E EAC DAC PEPD()2e e 7xf x ax =-+-7a =-()y f x =1x =[)()270,,4x f x x ∞∀∈+…a Mpa Mpa 22⨯0.10α=合格（桶）不合格（桶）合计新设备旧设备合计（2）从旧设备产品抽得的样本中随机抽取3桶，求抽到的不合格桶数的分布列和数学期望；（3）从该厂所有产品中任取一桶，用抽检频率估计概率，求抽到的一桶不合格的概率.参考公式：，其中.0.150.100.050.0252.0722.7063.8415.02422.（12分）已知椭圆的左，右顶点分别为，上，下顶点分别为，，四边形的内切圆的面积为，其离心率；抛物线的焦点与椭圆的右焦点重合.斜率为的直线过抛物线的焦点且与椭圆交于两点，与抛物线交于两点.（1）求椭圆及抛物线的方程；（2）是否存在常数，使得为一个与无关的常数？若存在，求出的值；若不存在，请说明理由.X ()()()()22()n ad bc a b c d a c b d χ-=++++n a b c d =+++αx α22122:1(0)x y E a b a b +=>>12,A A 1B 2B 1122A B A B 5π6e =22:2(0)E y px p =>1E k l 2E 1E ,A B 2E ,C D 1E 2E λ1AB CDλ+k λ南航附中2023-2024学年度第一学期期中考试高三数学一､单选题（每题5分）1.【答案】B【解析】解：由，得，由，得，.故选：B.2.【答案】C【解析】解：，，的实部是，故A 错误；的虚部是，故B 错误；复数在复平面内对应的点在第一象限，故C 正确；D 错误.故选：C.3.【答案】D【解析】解：向量在向量上的投影向量为，所以，又，所以.故选：D.4.【答案】A{}*24A x x x =∈N ∣…{}1,2,3,4A =B x y ⎧==⎨⎩()3,B =+∞(]{},3,1,2,3B A B =-∞⋂=R R ðð()12i 34i z +⋅=+ ()()()()34i 12i 34i 112i 12i 12i 12i 55z +-+∴===-++-z ∴115z 25-z 112,55⎛⎫⎪⎝⎭z ==ab 4b 24||a b b ⋅=2b = 16a b ⋅=【解析】解：因为，，故选：A.5.【答案】D 【解析】解：如图，取中点，连接，则，平面平面，平面平面，取的外心的外心，分别过作平面与平面的垂线交于点，即为球心，连接，由与均为边长为2的等边三角形，得三棱锥外接球的表面积.故选：D.6.【答案】B【解析】解：若，且公比，则，恒成立，故充分性成立；若，且时，tan 2α=-cos πcos 4αα∴====⎛⎫+ ⎪⎝⎭BD E ,AE CE ,AE BD CE BD ⊥⊥ ABD ⊥CBD AE ∴⊥,CBD CE ⊥ABD ABD V 1,O BCD V 2O 12,O O ABD BCD O O OC ABD V BCD V 221CO OO O E ===22222253R OC CO OO ∴==+=∴220π4π3S R ==10a >0q >110n n a a q -=>0n S ∴>10a >12q =-，由恒成立推不出，且公比，故必要性不成立，故“且公”是“恒成立”的充分不必要条件.故选：B.7.【答案】D【解析】解：设，则，则，故，线段的中点为，，故，又，则，即，，故椭圆的离心率，故椭圆离心率范围为，故选：D.8.【答案】C【解析】解：因为对任意，所以在上单调递增，111112212111(1)01323212n n nnn a S a a ⎡⎤⎛⎫--⎢⎥ ⎪⎡⎤⎡⎤⎝⎭⎢⎥⎛⎫⎛⎫⎣⎦==--=--⨯>⎢⎥⎢⎥ ⎪ ⎪⎛⎫⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦-- ⎪⎝⎭∴0n S >10a >0q >10a >0q >0n S >()()1122,,,A x y B x y 22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩22221212220x x y y a b --+=2121221212y y x x b x x a y y -+=--+ AB 1,(2)2P m m ⎛⎫> ⎪⎝⎭12122,1x x m y y ∴+=+=2122122y y mb x x a-=--121213y y x x -=--22213mb a -=-2216b a m =22112,612b m a m >∴=< C e =>=⎫⎪⎪⎭[)()()()()12122121,1,,0x x x x f x f x x x ∞⎡⎤∈+≠-⋅->⎣⎦()f x [)1,∞+又因为，所以，所以，即，所以在上恒成立，即以在上恒成立，令，则，问题转化为在上恒成立，又因为，当，即时，满足题意；当时，则有，解得：，综上所述，的取值范围为.故选：C.二､多选题（每题5分，漏选得2分，错选不得分）9.【答案】AC【解析】解：对于选项：因为随机变量，所以由可得：，所以本选项正确；对于选项B ：二项式的通项公式为，令，所以的系数为，因此本选项不正确；对于选项C ：由的意义可知的值越大，说明有更大的把握认为两事件有关系，因此本选项说法正确；()()22f x f x -+=()()22f x f x =--()()422622f x ax f x ++-…()()()()42222262222424f x axf x f xf x ⎡⎤+--=---=-⎣⎦…42224x ax x +-…[)1,∞+()42240x a x +-+…[)1,∞+2t x =1t …()2240t a t +-+…[)1,∞+2(2)16a =--V 0V …26a -……0>V ()2(2)16021212140a a a ⎧-->⎪-⎪-⎨⎪+-⨯+⎪⎩……6a >a [)2,∞-+A (),X B n p ~()()30,20E X D X ==()3011203np p np p =⎧⇒=⎨-=⎩5122x y ⎛⎫- ⎪⎝⎭52551551C (2)C 2(1)2rr r rr r r r r T x y x y ---+⎛⎫=⋅⋅-=⋅⋅-⋅⋅ ⎪⎝⎭3r =23x y 323535C 2(1)20⨯-⋅⋅-=-2χ2χ对于选项D ：因为样本相关系数越接近1，成对样本数据的线性相关程度越高，所以本选项说法不正确，故选：AC.10.【答案】ACD【解析】解：将函数的图象向右平移个单位长度，得到的图象，当，故在上是减函数，故A 正确；当时，，所以的图象不关于直线对称，所以，故B 错误；由于为奇函数，故C 正确；当，令，则，可得，故，即在上有4个零点，故D 正确，故选：ACD.11.【答案】AC【解析】解：表示第1次传球后球在甲手中的概率，所以，故正确；表示第2次传球后球在甲手中的概率，则，故错误；，即，故正确；，所以数列是首项为，公比为的等比数列，所以，r ()π2cos 24f x x ⎛⎫=-⎪⎝⎭π8()ππ2cos 22sin284y g x x x ⎡⎤⎛⎫==--= ⎪⎢⎥⎝⎭⎣⎦ππππ3π,,2,42444x x ⎡⎤⎡⎤∈-∈⎢⎥⎢⎥⎣⎦⎣⎦()y f x =ππ,42⎡⎤⎢⎥⎣⎦π4x =π4f ⎛⎫= ⎪⎝⎭()f x π4x =ππ44f x f x ⎛⎫⎛⎫-≠+⎪ ⎪⎝⎭⎝⎭()2sin2g x x =[][]π,π,22π,2πx x ∈-∈-()10g x -=2sin21x =1sin22x =11π7ππ5π2,,,6666x =--()1y g x =-[]π,π-1p 10p =A 2p 212p =B ()11012k k k p p p +=⨯+-⨯121k k p p ++=C 1111111111,22322323k k k k k p p p p p ++⎛⎫=-+-=-+-=-- ⎪⎝⎭13k p ⎧⎫-⎨⎬⎩⎭13-12-11111111,332332k k k k p p --⎛⎫⎛⎫-=-⨯-=-⨯- ⎪⎪⎝⎭⎝⎭，故D 错误.故选：AC.12.【答案】ABD【解答】解：由题意可知取得最大值时，曲率半径最大，取得最小值时，曲率半径最小，点在椭圆上，，，，当时，的最大值为，当时，的最小值为，由曲率半径公式为，可得曲率半径的最大值为，最小值为，故错误；若曲线上某点处的曲率半径越大，则曲线在该点处的弯曲程度越小，故A 正确；若某焦点在轴上的椭圆上一点处的曲率半径的最小值为（半焦距），则，，解得或（舍去），，故B 正确；若椭圆上所有点相应的曲率半径最大值为8，最小值为1，，解得，椭圆方程为，故D 正确.20222023202211111113323323p ⎛⎫=-⨯-=-⨯< ⎪⎝⎭220044x y a b+R R ()00,P x y 2222200002221,1x y x y b a b a ⎛⎫∴+=∴=- ⎪⎝⎭2220004422221111x y x a b b a a b ⎛⎫∴+=+- ⎪⎝⎭22022110,0x a a b -< (2)0x =220044x y a b+21b 22x a =220044x y a b+21a 3222220044x y R a b ab ⎛⎫=+ ⎪⎝⎭R 2a b 2b a C xc 2bc a=22220,10,10a ac c e e e e ∴--=∴--=+-=e =e =∴22221(0)x y a b a b +=>>228,1a b b a∴==4,2a b ==∴221164x y +=故选：ABD.三､填空题（每题5分）13.【答案】14或23【解析】解：的展开式中第9项､第10项､第11项的二项式系数成等差数列，则，即，化简整理可得，，解得或23.故答案为：14或23.14.【答案】【解析】解：角为的内角，，，，由正弦定理可知，，，，，，，，解得，设内切圆的半径为，内切圆面积为，，解得，，，当且仅当时，等号成立，(1n +8109C C 2C ,10nnnn +=…()()()!!2!8!8!10!10!9!9!n n n n n n +=---2373220n n -+=14n = ,,A B C ABC V πA B C ∴++=()sin sin2B Ca A Cb ++= πsin sin cos 222A A a B b b ⎛⎫∴=-= ⎪⎝⎭∴sin cossin sin 2AB A B =sin 0B > cos sin 2sin cos 222A A A A ∴==()0,πA ∈ cos02A∴>1sin 22A ∴=π26A ∴=π3A =ABC V r ABC V 4π2π4πr ∴=2r =()1π1sin 2232ABC S bc a b c ∴==⨯++V a b c =++222π2cos 23a b c bc bc bc bc =+--= …b c =，，解得，当且仅当时，等号成立，.故答案为：.15.【答案】0【解析】解：抛物线，导数为，设切点分别为，，切线的方程为，即，同理切线的方程为，又因为切线过点，所以得，①又因为切线也过点，所以得，②所以是方程的两实根，由韦达定理得，因为，所以，将代入，得，故答案为：0.a ∴…abc =+++…48bc …a b c ===ABC ∴V 48=2:4C x y =11242y x x =⋅='221212,,,44x x A x B x ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭1211,22MA MB k x k x ∴==MA ()2111142x y x x x -=-2111124y x x x =-MB 2221124y x x x =-MA ()0,1M x -201111124x x x -=-MB ()0,1M x -202211124x x x -=-12,x x 2011124x x x -=-120122,4x x x x x +==-2210120211,1,,144MA x x x MB x x x ⎛⎫⎛⎫=-+=-+ ⎪ ⎪⎝⎭⎝⎭ ()()22102012111144MA MB x x x x x x ⎛⎫⎛⎫⋅=--+++ ⎪⎪⎝⎭⎝⎭()()()22221201201212111164x x x x x x x x x x =-++++++()()()2221201201212121121164x x x x x x x x x x x x ⎡⎤=-+++++-+⎣⎦120122,4x x x x x +==-0MA MB ⋅=16.【答案】【解析】解：，则，因为，故，又当时，恒成立，即单调递增，所以，则，令，当时，，当时，，所以在处取得最小值，，即的最小值为.故答案为：.四､解答题（共70分）17.【答案】（1）；（2）.【解析】解：（1）是公比为的等比数列，，，则，①当时，，②由①-②得，，e()()()()ln 1ln e 1ln ln xg x x x x f x =+=+=()()12ln (1)f x f x m m ==>()()111e 11xf x x =+>10x >0x >()()1e 10xf x x =++>'()()e 1xf x x =+12ln x x =()()()111211121e 1ln ln ln ln ln x x x x f x x x x m m m m m m+++====()()2ln 1(1),ln (ln )x x h x x h x x x ->'==()1,e x ∈()0h x <()e,x ∞∈+()0h x '>()h x e x =()ee e lne h ==112ln x x x m+e e 2nn a =12121(1)n n T n +=--+2n n S a ⎧⎫-⎨⎬⎩⎭12112211S a ∴-=-=1122n n n S a -⎛⎫∴-= ⎪⎝⎭1122n n n S a -⎛⎫=-⎪⎝⎭2n …112122n n n S a ---⎛⎫=-⎪⎝⎭1112112222n n n n n n S S a a ----⎛⎫⎛⎫-=--- ⎪ ⎪⎝⎭⎝⎭即，即，数列是首项为2，公比为2的等比数列，所以.（2），可得.18.【答案】（1）见解析；（2）【解析】解：（1）证明：由于，所以，整理的，即，因为为锐角，所以，故，由为锐角可得；（2）由（1）得，因为，且由正弦定理得，所以，则112111222n n n n a a ---⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭()()11112212122n n nn n n a a -------∴=12nn a a -=∴{}n a 2nn a =()22122222221log log 211122(1)(1)log log nn n n n n n n a a n b a n n n n a a ++⎡⎤++=+=+=-+⎢⎥++⋅⎣⎦()222322111111222223(1)nn T n n ⎛⎫⎛⎫⎛⎫=-+-+⋯+-++++ ⎪⎪ ⎪+⎝⎭⎝⎭⎝⎭()12221211121(1)12(1)n n n n +-=-+=--+-+2564()()sin sin cos cos A B A C BC--=sin cos cos sin sin cos cos sin cos cos A B A B A C A CB C--=()cos sin cos cos sin 0A B C B C -=()cos sin 0A B C -=A cos 0A >()sin 0B C -=,B C B C =b c =sin 2a C =sin sin sin sin 2a C c A b A a B ====22,sin sin a b B A==()2222111sin sin 4A B a b +=+()221sin sin 4B B C ⎡⎤=++⎣⎦221sin sin 24B B ⎡⎤=+⎣⎦，因为所以，则，所以，根据二次函数的性质可知，当时，（*）取得最大值.19.【答案】（1；（2）存在点，理由见解析【解析】解：（1）取中点，连接，为等边三角形，.又平面底面，平面平面平面，平面.又在直角梯形中，易得；所以以为原点，为轴，为轴，为轴建立空间直角坐标系.则；，设平面的法向量为，则，令，得，又，故点到平面的距离.211cos21cos 242B B -⎛⎫=+- ⎪⎝⎭()2*113cos 2cos2488B B =--+π0,2π0π2,2B B ⎧<<⎪⎪⎨⎪<-<⎪⎩ππ42B <<π2π2B <<1cos20B -<<1cos24B =-25641,3PE E PD =AD O ,PO OC PAD V PO AD ∴⊥ PAD ⊥ABCD PAD ⋂,ABCD AD PO =⊂PAD PO ∴⊥ABCD ABCD OC AD ⊥O OC x OD y OPz (()()()(),0,1,0,1,1,0,1,0,0,0,1,0P A B C D --((),1,1,0CP CD ∴=-=-PDC (),,n x y z = 00n CP x n CD x y ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩ 1z =)n = ()0,1,0BC =B PCD BC n d n ⋅====（2）假设存在点，设，，，则，设平面的法向量为，则令，则，又平面的法向量为，于是化简，得.解得或（舍去），所以存在点，此时.20.【答案】（1）；（2）【解析】解：（1）当时，，则，则又，所以所求切线方程为，即.（2）等价于，①当时，显然成立；②当时，不等式等价于，E (),,,(01)E s t r PE PD λλ=<<((,,0,1,s t r λ∴-=()0,E λ∴()()1,1,0,0,AC AE λ==+-EAC (),,m a b c = ())0,10,m AC a b m AE b c λ⎧⋅=+=⎪⎨⋅=++=⎪⎩)1b λ=-)))11,1m λλλ=--+DAC (OP =cos ,OP m OP m OP m ⋅====231030λλ-+=13λ=3λ=E 13PE PD =()2e 7e 7y x =++-(2,e 7∞⎤--⎦7a =-()2e 7e 7xf x x =++-()e 7xf x '=+()1e 7f '=+()21e e f =+()()()2e e e 71y x -+=+-()2e 7e 7y x =++-[)()270,,4xf x x ∞∀∈+…[)2270,,e e 74x x ax x ∞∈+-+-…0x =2e 60-…0x >227e e 74xax x -+-…224e 74e 284x x a x-+-…设，则.设，则时，，当时，，则在上单调递减，上单调递增.因为，所以，且，则当时，，当时，.所以在上单调递减，在上单调递增，则，则，故的取值范围为.21.【答案】（1）不可以认为新设备比旧设备好；（2）见解析；（3）【解析】解：（1）易知抗张强度为合格品，否则为不合格品，在新设备和旧设备生产的产品中分别抽取了12桶和8桶，其中新设备中合格的有10桶，不合格的有2桶；旧设备中合格的有6桶，不合格的有2桶，列联表如下：合格（桶）不合格（桶）合计新设备10212旧设备628合计16420零假设：设备新旧与产品合格没有关系，此时，根据小概率值的独立性检验，没有充分证据推断不成立，则不可以认为新设备比旧设备好；()224e 74e 28x x g x x -+-=()()22241e 74e 28x x x g x x'---+=()()2241e 74e 28xh x x x =---+()()74e 1422e 7,0,ln2xxh x x x x x ⎛⎫=-=-∈ ⎪⎝⎭'()0h x '<7ln ,2x ∞⎫⎛⎫∈+ ⎪⎪⎝⎭⎭()0h x '>()h x 70,ln 2⎛⎫ ⎪⎝⎭7ln ,2∞⎛⎫+ ⎪⎝⎭()()2046e0h =-<7ln 02h ⎛⎫< ⎪⎝⎭()20h =()0,2x ∈()0g x '<()2,x ∞∈+()0g x '>()g x ()0,2()2,∞+()2min ()24e 28g x g ==-244e 28a -…a (2,e 7∞⎤--⎦15100Mpa …22⨯0H 2220(10262)0.2083 2.706128164χ⨯-⨯=≈<⨯⨯⨯0.10α=0H（2）易知的所有取值为，，则的分布列为：012此时；（3）易知该厂所有产品中新设备生产的占比为，旧设备生产的占比为，新设备的不合格率为，旧设备的不合格率，记“任取一桶产品不合格”为事件，记“产品为新设备生产”为事件，记“产品为旧设备生产”为事件，此时，可得，则从该厂所有产品中任取一桶，该桶不合格的概率为.22.【答案】（1）的方程为的方程为：；（2）.【解析】解：（1）已知椭圆，所以，则直线的方程为：，即因为四边形的内切圆的面积为，所以原点到直线，，①X 0,1,2()()()3211266262333888C C C C C 51530,1,2C 14C 28C 28P X P X P X =========X X P5141528328()515330121428284E X =⨯+⨯+⨯=12208201614A B C ()()()()1238211,,,20520564P B P C P A B P A C ======∣∣()()()()()3121156545P A P B P AB PC P A C =+=⨯+⨯=∣∣151E 2221,5x y E +=28y x =λ=22122:1x y E a b+=()()21,0,0,A a B b 21A B 1x ya b+=0,bx ay ab +-=1122A B A B 5π6O 21A B =因为椭圆离心率，所以，②又，③联立①②③，解得，所以梢圆的方程为，因为抛物线的焦点与椭圆的右焦点重合，所以，解得，则抛物线的方程为：.（2）由（1）知：抛物线焦点为，不妨设直线，联立，消去并整理得，由韦达定理得，所以联立，消去并整理得，由韦达定理得，因为直线过抛物线的焦点，e =c a =222a b c =+1,2a b c ===1E 2215x y +=22:2(0)E y px p =>1E 22pc ==4p =2E 28y x =2E ()2,0()()()()()()11223344:20,,,,,,,,l y k x k A x y B x y C x y D x y =-≠()22215y k x x y ⎧=-⎪⎨+=⎪⎩y ()222251202050k x k x k +-+-=2212122220205,5151k k x x x x k k -+==++2AB x =-===()228y k x y x⎧=-⎨=⎩y ()22224840k x k x k -++=234248k x x k ++=l 2E所以，此时，可得，所以，解得.()223422814844k k CD x x kk ++=++=+=()22181k AB CD k λλ+=+=+m =()22040k -+-=20040⎧-=⎪⎨-=⎪⎩λ=。

2020-2021学年江苏省南京市高二（上）期末数学试卷一、单项选择题（共8小题）.1．命题“∀a，b＞0，a+≥2和b+≥2至少有一个成立”的否定为（）A．∀a，b＞0，和至少有一个成立B．∀a，b＞0，和都不成立C．∃a，b＞0，和至少有一个成立D．∃a，b＞0，和都不成立2．已知a，b∈R，则“a+b＜0”是“a|a|+b|b|＜0”的（）A．必要不充分条件B．充分不必要条件C．充分必要条件D．既不充分也不必要条件3．自2010年以来，一、二、三线的房价均呈现不同程度的上升趋势，以房养老、以房为聘的理念深入人心，使得各地房产中介公司的交易数额日益增加．现将A房产中介公司2010﹣2019年4月份的售房情况统计如图所示，根据2010﹣2013年，2014﹣2016年，2017﹣2019年的数据分别建立回归直线方程、、，则（）A．，B．，C．，D．，4．在空间四边形ABCD各边AB、BC、CD、DA上分别取点E、F、G、H，若直线EF、GH相交于点P，则（）A．点P必在直线AC上B．点P必在直线BD上C．点P必在平面ABD内D．点P必在平面BCD内5．某校高一年级研究性学习小组利用激光多普勒测速仪实地测量复兴号高铁在某时刻的速度，其工作原理是：激光器发出的光平均分成两束射出，在被测物体表面汇聚，探测器接收反射光，当被测物体横向速度为零时，反射光与探测光频率相同，当横向速度不为零时，反射光相对探测光会发生频移，其中v为测速仪测得被测物体的横向速度，λ为激光波长，φ为两束探测光线夹角的一半，如图，若激光测速仪安装在距离高铁1m处，发出的激光波长为1500nm（1nm＝10﹣9m），某次检验中可测频移范围为9.500×109（1/h）至10.000×109（1/h），该高铁以运行速度（337.5km/h至375km/h）经过时，可测量的概率为（）A．B．C．D．6．已知A，B分别为双曲线实轴的左右两个端点，过双曲线Γ的左焦点F 作直线PQ交双曲线于P，Q两点（点P，Q异于A，B），则直线AP，BQ的斜率之比k AP：k BQ＝（）A．B．﹣3C．D．7．将边长为1的正方形ABCD沿对角线BD翻折，使得二面角A﹣BD﹣C的平面角的大小为，若点E，F分别是线段AC和BD上的动点，则的取值范围为（）A．[﹣1，0]B．C．D．8．在矩形ABCD中，AB＝4，，点G，H分别为直线BC，CD上的动点，AH交DG于点P．若，（0＜λ＜1），则点P的轨迹是（）A．直线B．抛物线C．椭圆D．双曲线二、多项选择题（共4小题）.9．对下列命题的否定说法正确是（）A．P：∀x∈R，x＞0；￢p：∃x∈R，x≤0B．P：∃x∈R，x2≤﹣1；￢p：∃x∈R，x2＞﹣1C．P：如果x＜2，那么x＜1；￢p：如果x＜2，那么x≥1D．P：∀x∈R，使x2+1≠0；￢p：∃x∈R，x2+1＝010．设同时抛掷两个质地均匀的四面分别标有1，2，3，4的正四面体一次．记事件A＝{第一个四面体向下的一面出现偶数}；事件B＝{第二个四面体向下的一面出现奇数}；C＝{两个四面体向下的一面或者同时出现奇数或者同时出现偶数}．给出下列说法：A．P（A）＝P（B）＝P（C）；B．P（AB）＝P（AC）＝P（BC）；C.；D.．其中正确的是（）A．A B．B C．C D．D11．正方体ABCD﹣A1B1C1D1的棱长为3，点E，F分别在棱CC1，D1C1上，且C1E＝2EC，D1F＝2FC1，下列命题：A．异面直线BE，CF所成角的余弦值为；B．过点B，E，F的平面截正方体，截面为等腰梯形；C．三棱锥B1﹣BEF的体积为；D．过B1作平面α，使得AE⊥α，则平面α截正方体所得截面面积为．其中所有真命题为（）A．A B．B C．C D．D12．已知椭圆M：（a＞b＞0）的左、右焦点分别为F1，F2，若椭圆M与坐标轴分别交于A，B，C，D四点，且从F1，F2，A，B，C，D这六点中，可以找到三点构成一个直角三角形，则椭圆M的离心率的可能取值为（）A．B．C．D．三、填空题（共4小题）.13．已知a∈R，命题p：∀x∈[1，2]，x2﹣a≥0，命题q：∃x∈R，x2+2ax+2﹣a＝0，若命题p ∧q为真命题，则实数a的取值范围是．14．假设要考察某公司生产的500克袋装牛奶的三聚青氨是否超标，现从800袋牛奶中抽取60袋进行检验，利用随机数表抽取样本时，先将800袋牛奶按000，001，…，799进行编号，如果从随机数表第7行第8列的数开始向右读，请你依次写出最先检测的3袋牛奶的编号．（下面摘取了随机数表第7行至第9行）84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 2583 92 12 06 7663 01 63 78 59 1695 56 67 19 98 10 50 71 75 12 86 73 58 0744 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 0744 38 15 51 00 13 4299 66 0279 5415．如图，一种电影放映灯的反射镜面是旋转椭圆面（椭圆绕其对称轴旋转一周形成的曲面）的一部分，过对称轴的截口BAC是椭圆的一部分，灯丝位于椭圆的一个焦点F1上，片门位于另一个焦点F2上．由椭圆一个焦点F1发出的光线，经过旋转椭圆面反射后集中到另一个焦点F2.已知BC⊥F1F2，|F1B|＝，|F1F2|＝4，则截口BAC所在椭圆的离心率为．16．如图，在△ABC中，AB＝1，，，将△ABC绕边AB翻转至△ABP，使面ABP⊥面ABC，D是BC的中点，设Q是线段PA上的动点，则当PC与DQ所成角取得最小值时，线段AQ的长度为．四、解答题（共70分）17．已知命题p：方程x2﹣2x+m＝0有两个不相等的实数根；命题q：2m+1＜4．（1）若p为真命题，求实数m的取值范围；（2）若p∨q为真命题，p∧q为假命题，求实数m的取值范围．18．有编号为1，2，3的三只小球，和编号为1，2，3，4的四个盒子，将三个小球逐个随机的放入四个盒子中、每只球的放置相互独立．（1）求三只小球恰在两个盒子中的概率；（2）求三只小球在三个不同的盒子，且至少有两个球的编号与所在盒子编号不同的概率．19．已知抛物线E：y2＝2px（p＞0）的焦点为F，直线l：y＝2x﹣2，直线l与E的交点为A，B．同时|AF|+|BF|＝8，直线m∥l．直线m与E的交点为C、D，与y轴交于点P．（I）求抛物线E的方程；（Ⅱ）若，求|CD|的长．20．“工资条里显红利，个税新政人民心”，随着2021年新年钟声的敲响，我国自1980年以来，力度最大的一次个人所得税（简称个税）改革至2019年实施以来发挥巨大作用．个税新政主要内容包括：（1）个税起征点为5000元；（2）每月应纳税所得额（含税）＝收入﹣个税起征点﹣专项附加扣除；（3）专项附加扣除包括住房、子女教育和赡养老人等．新旧个税政策下每月应纳税所得额（含税）计算方法及其对应的税率表如表：旧个税税率表（税起征点3500元）新个税税率表（个税起征点5000元）缴税级数每月应纳税所得额（含税）＝收税率（%）每月应纳税所得额（含税）＝收税率（%）入﹣个税起征点入﹣个税起征点﹣专项附加扣除1不超过1500元部分3不超过3000元部分32超过1500元至4500元部分10超过3000元至12000元部分103超过4500元至9000元的部分20超过12000元至25000元的部分204超过9000元至35000元的部分25超过25000元至35000元的部分255超过35000元至55000元部分30超过35000元至55000元部分30……………随机抽取某市1000名同一收入层级的IT从业者的相关资料，经统计分析，预估他们2021年的人均月收入24000元．统计资料还表明，他们均符合住房专项扣除；同时，他们每人至多只有一个符合子女教育扣除的孩子，并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2：1：1：1；此外，他们均不符合其他专项附加扣除．新个税政策下该市的专项附加扣除标准为：住房1000元/月，子女教育每孩1000元/月，赡养老人2000元/月等．假设该市该收入层级的IT从业者都独自享受专项附加扣除，将预估的该市该收入层级的IT从业者的人均月收入视为其个人月收入．根据样本估计总体的思想，解决如下问题：（1）求该市该收入层级的IT从业者2021年月缴个税的所有可能及其概率．（2）根据新旧个税方案，估计从2021年1月开始，经过多少个月，该市该收入层级的IT从业者各月少缴交的个税之和就超过2019年的月收入？21．如图，四棱锥P﹣ABCD中，侧棱PA垂直于底面ABCD，AB＝AC＝AD＝3，2AM＝MD，N为PB的中点，AD平行于BC，MN平行于面PCD，PA＝2．（1）求BC的长；（2）求二面角N﹣PM﹣D的余弦值．22．已知椭圆：C1：（a＞b＞0）的右顶点与抛物线C2：y2＝2px（p＞0）的焦点重合，椭圆C1的离心率为，过椭圆C1的右焦点F且垂直于x轴的直线截抛物线所得的弦长为．（Ⅰ）求椭圆C1和抛物线C2的方程；（Ⅱ）过点A（﹣4，0）的直线l与椭圆C1交于M，N两点，点M关于x轴的对称点为E．当直线l绕点A旋转时，直线EN是否经过一定点？请判断并证明你的结论．参考答案一、单项选择题（共8小题）.1．命题“∀a，b＞0，a+≥2和b+≥2至少有一个成立”的否定为（）A．∀a，b＞0，和至少有一个成立B．∀a，b＞0，和都不成立C．∃a，b＞0，和至少有一个成立D．∃a，b＞0，和都不成立解：根据含有量词的命题否定可知，∀a，b＞0，a+≥2和b+≥2至少有一个成立的否定为：∃a，b＞0，和都不成立．故选：D．2．已知a，b∈R，则“a+b＜0”是“a|a|+b|b|＜0”的（）A．必要不充分条件B．充分不必要条件C．充分必要条件D．既不充分也不必要条件解：由a+b＜0，可得a≤0，b＜0或a＞0，b＜﹣a，当a≤0，b＜0时，可得a|a|+b|b|＜0，当a＞0，b＜﹣a时，可得a|a|+b|b|＜0，故“a+b＜0”是“a|a|+b|b|＜0”的充分条件，由a|a|+b|b|＜0，可得当a≤0时，b＜0，或b＜﹣a，得a+b＜0；当a＞0时，可得b＜﹣a，得a+b＜0，故“a+b＜0”是“a|a|+b|b|＜0”的必要条件，∴a，b∈R，则“a+b＜0”是“a|a|+b|b|＜0”的充分必要条件，故选：C．3．自2010年以来，一、二、三线的房价均呈现不同程度的上升趋势，以房养老、以房为聘的理念深入人心，使得各地房产中介公司的交易数额日益增加．现将A房产中介公司2010﹣2019年4月份的售房情况统计如图所示，根据2010﹣2013年，2014﹣2016年，2017﹣2019年的数据分别建立回归直线方程、、，则（）A．，B．，C．，D．，解：回归直线分布在散点图附近，表示回归直线的斜率，表示回归直线在y轴上的截距，由题意可知，2010﹣2013年，y随x的增加而迅速增加，2014﹣2016年，y随x的增加而平缓增加，2017﹣2019年，y随x的增加而减少，故，由图可知，，故选：A．4．在空间四边形ABCD各边AB、BC、CD、DA上分别取点E、F、G、H，若直线EF、GH 相交于点P，则（）A．点P必在直线AC上B．点P必在直线BD上C．点P必在平面ABD内D．点P必在平面BCD内解：作图如下：因为EF属于一个面，而GH属于另一个面，且EF和GH能相交于点P，所以P在两面的交线上，因为AC是两平面的交线，所以点P必在直线AC上．故选：A．5．某校高一年级研究性学习小组利用激光多普勒测速仪实地测量复兴号高铁在某时刻的速度，其工作原理是：激光器发出的光平均分成两束射出，在被测物体表面汇聚，探测器接收反射光，当被测物体横向速度为零时，反射光与探测光频率相同，当横向速度不为零时，反射光相对探测光会发生频移，其中v为测速仪测得被测物体的横向速度，λ为激光波长，φ为两束探测光线夹角的一半，如图，若激光测速仪安装在距离高铁1m处，发出的激光波长为1500nm（1nm＝10﹣9m），某次检验中可测频移范围为9.500×109（1/h）至10.000×109（1/h），该高铁以运行速度（337.5km/h至375km/h）经过时，可测量的概率为（）A．B．C．D．解：sinφ＝＝，＝，当高铁以运行速度337.5km/h经过时，频移为≈8.998×109（1/h）；当高铁以运行速度375km/h经过时，频移为≈9.998×109（1/h）．则频移范围为9.998×109（1/h）至8.998×109（1/h），又检验中可测频移范围为9.500×109（1/h）至10.000×109（1/h），∴该高铁以运行速度（337.5km/h至375km/h）经过时，可测量的概率为P＝＝．故选：A．6．已知A，B分别为双曲线实轴的左右两个端点，过双曲线Γ的左焦点F 作直线PQ交双曲线于P，Q两点（点P，Q异于A，B），则直线AP，BQ的斜率之比k AP：k BQ＝（）A．B．﹣3C．D．解：由已知得双曲线Γ：a＝1，b＝，c＝2．故F（﹣2，0），A（﹣1，0），B（1，0）．设直线PQ：x＝my﹣2，且P（x1，y1），Q（x2，y2）．由消去x整理得（3m2﹣1）y2﹣12my+9＝0，∴，两式相比得①，∴k AP：k BQ＝＝＝②，将①代入②得：上式＝＝﹣3．故k AP：k BQ＝﹣3．故选：B．7．将边长为1的正方形ABCD沿对角线BD翻折，使得二面角A﹣BD﹣C的平面角的大小为，若点E，F分别是线段AC和BD上的动点，则的取值范围为（）A．[﹣1，0]B．C．D．解：如图，＝（）•（）＝++＝0﹣（+）+0＝﹣（+），∵，∴∈[﹣]，∵OC＝OA＝，二面角A﹣BD﹣C的平面角的大小为，∴∈[]，∴∈[﹣1，]．故选：B．8．在矩形ABCD中，AB＝4，，点G，H分别为直线BC，CD上的动点，AH交DG于点P．若，（0＜λ＜1），则点P的轨迹是（）A．直线B．抛物线C．椭圆D．双曲线解：分别以MN和AD所在的直线为x，y轴建立平面直角坐标系，则，，M（2，0），N（﹣2，0），因为，（0＜λ＜1），所以，，所以直线AH的方程为，直线DG的方程为，联立这两条件直线方程可得点因为，则点P的坐标满足，所以点P的轨迹是以O为对称中心，N，M分别为左右焦点的椭圆，其中a＝4，，c＝2．故选：C．二、多项选择题（本大题共4小题，每小题5分，共20分，在每小题给出的选项中，有多项是符合题目要求的全部选对的得5分，有选错的得0分，部分选对的得3分）9．对下列命题的否定说法正确是（）A．P：∀x∈R，x＞0；￢p：∃x∈R，x≤0B．P：∃x∈R，x2≤﹣1；￢p：∃x∈R，x2＞﹣1C．P：如果x＜2，那么x＜1；￢p：如果x＜2，那么x≥1D．P：∀x∈R，使x2+1≠0；￢p：∃x∈R，x2+1＝0解：P：∀x∈R，x＞0；￢p：∃x∈R，x≤0，A正确；P：∃x∈R，x2≤﹣1；￢p：∀x∈R，x2＞﹣1，B错误；P：如果x＜2，那么x＜1；￢p：如果x＜2，那么x≥1，C正确；P：∀x∈R，使x2+1≠0；￢p：∃x∈R，x2+1＝0，D正确．故选：ACD．10．设同时抛掷两个质地均匀的四面分别标有1，2，3，4的正四面体一次．记事件A＝{第一个四面体向下的一面出现偶数}；事件B＝{第二个四面体向下的一面出现奇数}；C＝{两个四面体向下的一面或者同时出现奇数或者同时出现偶数}．给出下列说法：A．P（A）＝P（B）＝P（C）；B．P（AB）＝P（AC）＝P（BC）；C.；D.．其中正确的是（）A．A B．B C．C D．D解：同时抛掷两个质地均匀的四面分别标有1，2，3，4的正四面体一次．记事件A＝{第一个四面体向下的一面出现偶数}，则P（A）＝＝，事件B＝{第二个四面体向下的一面出现奇数}，则P（B）＝＝，C＝{两个四面体向下的一面或者同时出现奇数或者同时出现偶数}，则P（C）＝＝，∴P（A）＝P（B）＝P（C），故A正确；∵A，B，C是相互独立事件，∴P（AB）＝P（AC）＝P（BC）＝＝，故B正确；∵A、B、C不是两两互斥事件，∴不正确，故C错误；∵P（A）＝P（B）＝P（C）＝，∴，故D正确．故选：ABD．11．正方体ABCD﹣A1B1C1D1的棱长为3，点E，F分别在棱CC1，D1C1上，且C1E＝2EC，D1F＝2FC1，下列命题：A．异面直线BE，CF所成角的余弦值为；B．过点B，E，F的平面截正方体，截面为等腰梯形；C．三棱锥B1﹣BEF的体积为；D．过B1作平面α，使得AE⊥α，则平面α截正方体所得截面面积为．其中所有真命题为（）A．A B．B C．C D．D解：对于A．取A1B1的三等分点为F1，使A1F1＝2F1B1，又D1F＝2FC1，∴F1B1∥FC1且F1B1＝FC1，∴四边形FC1B1F1为平行四边形，∴FF1∥B1C1∥BC且FF1＝B1C1＝BC，∴四边形F1FCB为平行四边形，∴BF1∥CF，则∠F1BE为异面直线BE，CF所成的角，连接EF1，由题意得：BF1＝，BE＝，EF1＝，所以cos∠F1BE＝＝＝，故A正确；对于B．取B1B的三等分点为E1，使B1E1＝2E1B，又C1E＝2EC，∴BE1∥CE且BE1＝CE，∴四边形BE1EC为平行四边形，则E1E∥BC且E1E＝BC，又由A得，FF1∥BC且FF1＝BC，于是FF1∥EE1且FF1＝EE1，∴四边形EE1F1F为平行四边形，∴EE1∥F1F，取A1B1的中点为G，连接BG，又＝＝，∴E1F1∥BG∥EF，则四边形BEFG即为所求截面，由题意知：BE≠FG，故B不正确；对于C．S△B1BE＝×3×3＝，又C1F⊥面B1BE，C1F＝1，所以＝＝×C1F＝＝××1＝，故C正确；对于D．取CD的三等分点为H1，使CH1＝2DH1，取BC的三等分点为H，使CH＝2BH，∴HH1∥BD∥B1D1，则面B1D1H1H即为所求的截面α，建立如图所示的空间坐标系，则A（3，0，0），E（0，3，1），B1（3，3，3），D1（0，0，3），H1（0，1，0），＝（﹣3，3，1），＝（﹣3，﹣3，0），＝（﹣3，﹣2，﹣3），∵•＝0，•＝0，所以AE⊥平面B1D1H1H，由已知条件得，B1D1＝3，HH1＝B1D1＝2，B1H＝D1H1＝，等腰梯形B1D1H1H的高为h＝＝，所以截面面积为S＝×＝，故D正确．故选：ACD．12．已知椭圆M：（a＞b＞0）的左、右焦点分别为F1，F2，若椭圆M与坐标轴分别交于A，B，C，D四点，且从F1，F2，A，B，C，D这六点中，可以找到三点构成一个直角三角形，则椭圆M的离心率的可能取值为（）A．B．C．D．解：由题意可得左右焦点和上下顶点可能构成直角三角形，这时b＝c，离心率e＝＝＝；或者长轴的点和短轴的点和一个焦点可能构成直角三角形，如图所示：这时AF22＝AB2+BF22，即（a+c）2＝a2+b2+a2，整理可得：e2+e﹣1＝0，可得e＝，故选：BC．三、填空题（本大题共4小题，每小题5分，共20分，把答案填写在答题卡相应位置上）13．已知a∈R，命题p：∀x∈[1，2]，x2﹣a≥0，命题q：∃x∈R，x2+2ax+2﹣a＝0，若命题p ∧q为真命题，则实数a的取值范围是a≤﹣2，或a＝1．解：若命题p：“∀x∈[1，2]，x2﹣a≥0”为真；则1﹣a≥0，解得：a≤1，若命题q：“∃x∈R，x2+2ax+2﹣a＝0”为真，则△＝4a2﹣4（2﹣a）≥0，解得：a≤﹣2，或a≥1，若命题“p∧q”是真命题，则a≤﹣2，或a＝1，故答案为：a≤﹣2，或a＝114．假设要考察某公司生产的500克袋装牛奶的三聚青氨是否超标，现从800袋牛奶中抽取60袋进行检验，利用随机数表抽取样本时，先将800袋牛奶按000，001，…，799进行编号，如果从随机数表第7行第8列的数开始向右读，请你依次写出最先检测的3袋牛奶的编号331、572、455．（下面摘取了随机数表第7行至第9行）84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 2583 92 12 06 7663 01 63 78 59 1695 56 67 19 98 10 50 71 75 12 86 73 58 0744 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 0744 38 15 51 00 13 4299 66 0279 54解：利用随机数表抽取是样本数据，找到第7行第8列的数开始向右读，第一个符合条件的是331，第二个数是572，第三个数是455．故答案为：331，572，455．15．如图，一种电影放映灯的反射镜面是旋转椭圆面（椭圆绕其对称轴旋转一周形成的曲面）的一部分，过对称轴的截口BAC是椭圆的一部分，灯丝位于椭圆的一个焦点F1上，片门位于另一个焦点F2上．由椭圆一个焦点F1发出的光线，经过旋转椭圆面反射后集中到另一个焦点F2.已知BC⊥F1F2，|F1B|＝，|F1F2|＝4，则截口BAC所在椭圆的离心率为．解：由题意可得2c＝4，＝，c2＝a2﹣b2，解得a＝6，所以离心率e＝＝＝，故答案为：．16．如图，在△ABC中，AB＝1，，，将△ABC绕边AB翻转至△ABP，使面ABP⊥面ABC，D是BC的中点，设Q是线段PA上的动点，则当PC与DQ所成角取得最小值时，线段AQ的长度为．解：过点P作PO⊥平面ABC，交BA延长线于点O，连结OC，以O为原点，OB为x轴，OC为y轴，OP为z轴，建立空间直角坐标系，在△ABC中，AB＝1，BC＝2，B＝，将△ABC绕边AB翻转至△ABP，使平面ABP⊥平面ABC，D是BC的中点，设Q是线段PA上的动点，则B（2，0，0），A（1，0，0），O（0，0，0），C（0，2，0），P（0，0，2），设Q（x，y，z），＝＝λ（﹣1，0，2），λ∈[0，1]，即（x﹣1，y，z）＝（﹣λ，0，2λ），∴Q（1﹣λ，0，2λ），D（1，1，0），＝（﹣λ，﹣1，2λ），＝（0，2，﹣2），|cos＜＞|＝＝，令f（λ）＝，λ∈[0，1]，∴f′（λ）＝，由f′（λ）＝0，λ∈[0，1]，得，λ∈[0，）时，f′（λ）＞0，λ∈（，1]时，f′（x）＜0，∴当时，f（λ）取最大值，此时PC与DQ所成角取得最小值，|AQ|＝||＝．故答案为：．四、解答题（共70分。

江苏省南京市2020-2021学年高二上学期期中调研测试数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．在平面直角坐标系xoy 中，已知抛物线x 2=2y 的焦点为F ，准线为l ，则点F 到准线l 的距离为（ ） A ．12B ．1C ．2D ．42．已知向量()2,3,1a =--，()4,,b m n =，且//a b ，其中m 、n R ∈，则m n +=（ ） A ．4B ．4-C ．2D ．2-3．若sin θ=2cos (π-θ)，则tan 4πθ⎛⎫+ ⎪⎝⎭的值为（ ） A ．3B ．13 C ．3-D ．13-4．在平面直角坐标系xoy 中，若椭圆22:19x y C m +=与双曲线22:1y T x m-=有相同的焦点，则双曲线T 的渐近线方程为（ ） A ．14y x =±B ．12y x =±C ．4y x =±D ．2y x =±5．在平面直角坐标系xOy 中，直线240x y +-=与两坐标轴分别交于点A 、B ，圆C 经过A 、B ，且圆心在y 轴上，则圆C 的方程为（ ） A ．226160x y y ++-= B ．226160x y y +--= C ．22890x y y ++-=D ．22890x y y +--=6．如图，已知圆柱的底面半径为2，与圆柱底面成60角的平面截这个圆柱得到一个椭圆，则该椭圆的焦距为（ ）A ．B ．C ．D ．7．如图，在三棱柱ABC -A 1B 1C 1中，BC 1与B 1C 相交于点O ，∠A 1AB =∠A 1AC =60，∠BAC =90，A 1A =3，AB =AC =2，则线段AO 的长度为（ ）A BC ．2D 8．在平面直角坐标系xoy 中，已知双曲线()2222:10,0x y C a b a b-=>>的左焦点为F ，点M ，N 在双曲线C 上，若四边形OFMN 为菱形，则双曲线C 的离心率为（ ）A 1B 1-C 1D 1二、多选题9．已知两个不重合的平面α，β及直线m ，下列说法正确的是（ ） A ．若α⊥β，m ⊥α， 则m //β B ．若α/β，m ⊥α， 则m ⊥β C ．若m //α，m ⊥β， 则α⊥βD ．若m //α，m //β， 则α//β10．在平面直角坐标系xoy 中，F 1，F 2分别为椭圆 22142x y +=的左、右焦点，点A 在椭圆上.若△AF 1F 2为直角三角形，则AF 1的长度可以为（ ） A ．1B ．2C ．3D ．411．如图，直线12,l l 相交于点O ，点P 是平面内的任意一点，若x ，y 分别表示点P 到12,l l 的距离，则称（x ，y ）为点P 的“距离坐标”.下列说法正确的是（ ）A ．距离坐标为（0，0）的点有1个B ．距离坐标为（0，1）的点有2个C ．距离坐标为（1，2）的点有4个D ．距离坐标为（x ，x ）的点在一条直线上12．20世纪50年代，人们发现利用静态超高压和高温技术，通过石墨等碳质原料和某些金属反应可以人工合成金刚石，人工合成金刚石的典型晶态为立方体（六面体）、八面体和立方八面体以及他们的过渡形态. 其中立方八面体（如图所示）有24条棱、12个顶点，14个面（6个正方形、8个正三角形），它是将立方体“切”去8个“角”后得到的几何体.已知一个立方八面体的棱长为1，则（ ）A ．它的所有顶点均在同一个球面上，且该球的直径为2B ．它的任意两条不共面的棱所在的直线都互相垂直C D ．它的任意两个共棱的面所成的二面角都相等三、填空题13．在平面直角坐标系xOy 中，已知直线1:0l x ay +=和直线()2:2340l x a y ---=，a R ∈，若1l 与2l 平行，则1l 与2l 之间的距离为_________.14．在空间直角坐标系中，若三点A （1，-1，a ），B (2，a ，0)，C (1，a ，-2)满足：2A AB BC C →→→⎛⎫-⊥ ⎪⎝⎭，则实数a 的值为_________. 15．词语“堑堵”、“阳马”、“鳖臑”等出现自中国数学名著《九章算术•商功》，是古代人对一些特殊锥体的称呼.在《九章算术•商功》中，把四个面都是直角三角形的四面体称为“鳖臑”，现有如图所示的“鳖臑”四面体P ABC ，其中P A ⊥平面ABC ，P A =AC =1，BC ，则四面体P ABC 的外接球的表面积为________.16．早在一千多年之前，我国已经把溢流孔技术用于造桥，以减轻桥身重量和水流对桥身的冲击，现设桥拱上有如图所示的4个溢流孔，桥拱和溢流孔轮廓线均为抛物线的一部分，且四个溢流孔轮廓线相同，建立如图所示的平面直角坐标系xoy ，根据图上尺寸， 溢流孔ABC 所在抛物线的方程为_________， 溢流孔与桥拱交点A 的横坐标．．．为 ___________ .四、解答题17．在①sin (A -B )=sin B +sin C ；②2a cos C =2b +c ；③△ABC 的面积S =a 2-b 2-c 2）三个条件中任选一个（填序号），补充在下面的问题中，并解答该问题.已知△ABC 的内角A 、B 、C 的对边分别为a ，b ，c ， ，D 是边BC 上的一点，∠BAD =2π，且 b =4，c =2，求线段AD 的长.注：如果选择多个条件分别解答，按第一个解答计分 18．在平面直角坐标系xoy 中，已知圆F ：（x -2）2+y 2=1，动圆M 与直线l ：x =-1相切且与圆F 外切.(1)记圆心M 的轨迹为曲线C ，求曲线C 的方程；(2)已知A （-2，0），曲线C 上一点P 满足P A PF ，求∠P AF 的大小. 19．如图，在直三棱柱111ABC A B C -中，D 为AC 的中点.（1）求证：1//B A 平面1C BD ；（2）若13AA AB ==，4BC =，且AB BC ⊥，求三棱锥11B B C D -的体积. 20．在平面直角坐标系xoy 中，已知圆O ：x 2+y 2=1，点A ，B 是直线x -y +m =0(m ∈R )与圆O 的两个公共点，点C 在圆O 上.（1）若△ABC 为正三角形，求直线AB 的方程；（2）若直线x -y =0上存在点P 满足0AP BP ⋅=，求实数m 取值范围.21．如图，在四棱锥P ABCD -中，平面PAB ⊥平面ABCD ，PA AB ⊥，4PA AD ==，//BC AD ，AB AD ⊥，2AB BC ==，()01PE PC λλ=≤≤.（1）若12λ=，求直线DE 与平面ABE 所成角的正弦值；（2）设二面角B AE C --的大小为θ，若cos 17θ=，求λ的值. 22．在平面直角坐标系xoy 中，已知椭圆()2222:10x y C a b a b+=>>的左顶点与上顶点的距离为(.（1）求椭圆C的方程.（2）直线l与椭圆C相交于P、Q两点，M是PQ的中点.若椭圆上存在点N满足 ，求证：△PQN的面积S为定值.3ON MO参考答案1．B 【分析】由抛物线的标准方程可知p ，即可求解. 【详解】因为抛物线x 2=2y ， 所以22p =，即1p =， 所以焦点F 到准线l 的距离为1， 故选：B 2．B 【分析】由//a b 列等式可求出m 、n 的值，进而可求得m n +的值. 【详解】向量()2,3,1a =--，()4,,b m n =，且//a b ，4231m n∴==--，解得62m n =-⎧⎨=⎩，因此，4m n +=-. 故选：B. 3．D 【分析】根据诱导公式化简可求出tan θ，利用两角和的正切公式求值即可. 【详解】由诱导公式可知，sin 2cos()2cos θπθθ=-=-，则tan 2θ=-， 所以1tan 1(2)1tan()41tan 1(2)3πθθθ++-+===----，故选：D 4．D 【分析】本题首先可根据双曲线解析式得出焦点在x 轴上，然后令焦距为2c ，根据椭圆与双曲线的a 、b 、c 三者之间的关系解得4m =，最后根据双曲线方程即可求出渐近线方程.【详解】因为椭圆22:19x y C m +=与双曲线22:1y T x m-=有相同的焦点，所以它们的焦点在x 轴上， 令焦距为2c ，则291mc m ，解得4m =，双曲线22:14y T x -=，故双曲线T 的渐近线方程为2y x =±， 故选：D. 【点睛】本题考查根据椭圆与双曲线共焦点求双曲线的渐近线方程，在椭圆22221x y a b+=中有222a cb -=，在双曲线22221x y a b -=中有222+=a b c ，且双曲线22221x y a b-=的渐近线方程为by x a=±，要注意焦点在x 轴还是在y 轴上，考查计算能力，是中档题. 5．A【分析】求出点A 、B 的坐标，设圆心坐标为()0,b ，由AC BC =可求出圆心C 的坐标，并求出圆的半径，由此可求得圆C 的方程. 【详解】易知，直线240x y +-=交x 轴于点()4,0A ，交y 轴于点()0,2B ，设圆心C 的坐标为()0,b ，由AC BC =2b =-，解得3b =-， 所以，圆C 的半径为325BC =--=，因此，圆C 的方程为()22325x y ++=，即为226160x y y ++-=.故选：A.【点睛】求圆的方程，主要有两种方法：（1）几何法：具体过程中要用到初中有关圆的一些常用性质和定理．如：①圆心在过切点且与切线垂直的直线上；②圆心在任意弦的中垂线上；③两圆相切时，切点与两圆心三点共线；（2）待定系数法：根据条件设出圆的方程，再由题目给出的条件，列出等式，求出相关量．一般地，与圆心和半径有关，选择标准式，否则，选择一般式．不论是哪种形式，都要确定三个独立参数，所以应该有三个独立等式． 6．D 【分析】如图所示，设椭圆的长轴为AB ，短轴为CD ，中心为点1O 、圆柱的底面中心为O ，则60OAB ︒∠=，可得1||a O A =， b ，求出c ，然后求解结果．【详解】 如图所示，设椭圆的长轴为AB ，短轴为CD ，中心为点1O ，圆柱的底面中心为O ， 则60OAB ︒∠=， 可得1||||4cos60OA a O A ︒===，1||22b CD ==c ∴==∴椭圆的焦距为: 故选：D 7．A 【分析】用1,,AB AC AA 表示出AO→，计算2AO →，开方得出AO 的长度.【详解】因为四边形11BCC B 是平行四边形，()111122BO BC BC BB ∴==+, 111111122222AO AB BO AB BC AA AC AB AA ∴=+=++=++11160,90,3,2,A AB A AC BAC A A AB AC ︒︒∠=∠=∠====22214,9,0AB AC AA AB AC ∴===⋅=,1132cos603AB AA AC AA ⋅=⋅=⨯⨯=,()22114AO AB AC AA ∴=++, ()22211112224AB AC AA AB AC AB AA AC AA =+++⋅+⋅+⋅ 294=||AO →∴=，即AO =故选：A 8．C 【分析】利用四边形OFMN(O 为坐标原点)为菱形，结合双曲线的对称性，求出M 的坐标，代入双曲线方程然后求解离心率. 【详解】由题意可知||OF c =，由四边形OFMN 为菱形，可得||||MN OF c ==，设点M 在F 的上方，可知M 、N 关于y轴对称，可设(2c M -，代入双曲线方程可得: 2222()(221c a b --=， 又由222+=a b c ，化简可得4422480,c a a c +-= 两边同除以4a ，可得42480e e +-=，解得24e =+ 因为1e >，解得1e ===，故选：C 【点睛】关键点点睛：根据四边形OFMN(O 为坐标原点)为菱形，||||MN OF c ==，能写出点M 的坐标，是建立方程的关键，结合双曲线的对称性，发现M 点横坐标为2c-是突破口. 9．BC 【分析】根据线面和面面的位置关系依次判断选项即可得到答案. 【详解】对选项A ，若αβ⊥，m α⊥，则//m β或m β⊂，故A 错误； 对选项B ，若//αβ，m α⊥，则m β⊥，故B 正确； 对选项C ，若//m α，则平面α内存在直线l ，使得//l m ， 又m β⊥，所以l β⊥，故αβ⊥，故C 正确；对选项D ，若//m α，//m β，则//αβ或α与β相交，故D 错误. 故选：BC 10．ABC【分析】利用已知条件判断三角形的直角顶点的位置，转化求解AF 1的长，判断选项即可. 【详解】由椭圆 22142x y +=可知，2,a b c ===焦点坐标为(，通径为222b a=，因为△AF 1F 2为直角三角形，所以A 为直角顶点时，A 在短轴端点，此时AF 1的长为2；1F 为直角顶点时，A 在y 轴左侧，此时AF 1的长为1;2F 为直角顶点时，A 在y 轴右侧，此时AF 1的长为3;故选：ABC. 11．ABC 【分析】根据题意，依次分析选项是否正确，综合即可得答案． 【详解】对于A ，若距离坐标为（0，0)，即P 到两条直线的距离都为0，P 为两直线的交点，即距离坐标为（0，0)的点只有1个，A 正确，对于B ，若距离坐标为(0，1)，即P 到直线1l 的距离为0，到直线2l 的距离为1，P 在直线1l 上，到直线2l 的距离为1，符合条件的点有2个，B 正确，对于C ，若距离坐标为（1，2)，即P 到直线1l 的距离为1，到直线2l 的距离为2，有4个符合条件的点，即四个交点为与直线1l 相距为2的两条平行线和与直线2l 相距为1的两条平行线的交点，C 正确，对于D ，若距离坐标为（x ，x )，即P 到两条直线的距离相等，则距离坐标为(x ，x )的点在2条相互垂直的直线上，D 错误， 故选：ABC 12．ACD 【分析】利用立方八面体与正方体之间的关系计算出正方体的棱长，可判断A 、C 选项的正误；计算出不共面的棱所成角的大小可判断B 选项的正误，计算相邻的两个面所成二面角的大小可判断D 选项的正误. 【详解】如下图所示，由题意可知，立方八面体的顶点为正方体1111ABCD A B C D -各棱的中点， 故立方八面体的棱为正方体1111ABCD A B C D -相邻两条棱的中点的连线，=由对称性可知，立方八面体的外接球球心为正方体1111ABCD A B C D -的中心，外接球的直径为正方体1111ABCD A B C D -的面对角线长2，该球的半径为1，A 选项正确； 设MN 、PQ 为立方八面体的两条不共面的棱，如下图所示，则11//MN B D ，在正方体1111ABCD A B C D -中，11//BB DD 且11BB DD =，则四边形11BB D D 为平行四边形，11//BD B D ∴，//MN BD ∴，由于1//PQ BC ，易知1BC D 为等边三角形，则160C BD ∠=，所以，MN 与PQ 所成角为60，B 选项错误；立方八面体的体积为331183223V ⎛=-⨯⨯⨯= ⎝⎭C 选项正确； 设正方体1111ABCD A B C D -底面的中心为点O ，连接OC 交立方八面体的棱PF 于点E ， 连接EQ ，则E 为PF 的中点，且PFQ △为等边三角形，所以，EQ PF ⊥，CD BC =，O 为BD 的中点，OC BD ∴⊥，P 、F 分别为BC 、CD 的中点，则//PF BD ，OC PF ∴⊥，所以，OEQ ∠为立方八面体的底面与由平面PFQ 所成二面角的平面角，立方八面体的棱长为1，12OE EC ∴==，1122CQ CC ==，3sin 602EQ PQ ==， 1CC ⊥平面ABCD ，CE ⊂平面ABCD ，1CC CE ∴⊥，在Rt CEQ 中，cos CE CEQ EQ ∠==所以，()cos cos 180cos 3OEQ CEQ CEQ ︒∠=-∠=-∠=-，同理可知，立方八面体的相邻两个面所成二面角的余弦值为3-，D 选项正确. 故选：ACD.【点睛】作二面角的平面角可以通过垂线法进行，在一个半平面内找一点作另一个半平面的垂线，再过垂足作二面角的棱的垂线，两条垂线确定的平面和二面角的棱垂直，由此可得二面角的平面角．13 【分析】利用两直线平行求出参数a 的值，然后利用平行线间的距离公式可求得直线1l 与2l 之间的距离. 【详解】由于直线1l 与2l 平行，则()23a a =--，解得1a =，所以，直线1l 的方程为0x y +=，直线2l 的方程为20x y +-=，因此，直线1l 与2l 之间的距离为d ==. 14．92-【分析】先根据点的坐标得到,AB BC →→，AC →的坐标表示，再根据向量垂直对应的数量积为零计算出a 的值即可.【详解】由题意(1,1,),(0,1,2),(1,0,2)AB a a a B A a C C →→→=+-=+--=--，所以(2)(1,1,4)(1,0,2)12(4)290AB BC a a a C a A →→→-⋅=--+⋅--=--+=--=， 解得92a =-. 故答案为：92-15．4π 【分析】根据“鳖臑”四面体P ABC 的特征，可确定外接球球心为PB 的中点，即可求解. 【详解】 如图，由题意90ACB ∠=︒,则取PB 的中点为点O ， 可得OA OB OP OC ===，即O 为球心，则其半径112R PB ====， 则其表面积为244S R ππ==， 故答案为：4π 16．()236145x y -=-14013【分析】根据题意，设桥拱所在抛物线的方程为22x py =-，溢流孔ABC 所在方程为()21:142(0)C x p y p ''-=->，运用待定系数法，求得p ，p '，可得右边第二个溢流孔所在方程，联立抛物线方程，可得所求. 【详解】设桥拱所在抛物线方程22x py =-，由图可知，曲线经过()20,5-，代入方程()22025p =-⨯-，解得：40p =，所以桥拱所在抛物线方程280x y =-； 四个溢流孔轮廓线相同，所以从右往左看， 设第一个抛物线()21:142C x p y '-=-，由图抛物线1C 经过点()20,5A -，则()()2201425p '-=-⨯-，解得185p '=， 所以()2136:145C x y -=-， 点A 即桥拱所在抛物线280x y =-与()2136:145C x y -=-的交点坐标， 设(),,714A x y x <<由()228036145714x y x y x ⎧=-⎪⎪-=-⎨⎪<<⎪⎩，解得：14013x = 所以点A 的横坐标为14013. 故答案为：()236145x y -=-；14013【点睛】关键点点睛：此题考查根据实际意义求抛物线方程和交点坐标，关键在于合理建立模型正确求解，根据待定系数法，及平移抛物线后方程的形式即可. 17．选择条件①②③，AD =.【分析】首先选择条件②，利用正弦定理，结合三角形内角和以及诱导公式求得1cos 2A =-，得到23A π=，利用余弦定理求得a =cos B =三角形ABD △中，求得结果. 【详解】 若选①，因为sin (A -B )=sin B +sin C ，所以sin cos cos sin sin sin cos cos sin A B A B B A B A B -=++，即sin 2cos sin 0B A B +=，因为sin 0B >，所以1cos 2A =-，因为(0,)A π∈，所以23A π=，由余弦定理可得2222cos 1644228a b c bc A =+-=++⨯=，所以a =222cos2a c b B ac +-====，所以在ABD △中，2cos AB B BD BD ===BD =所以AD =选择条件②；因为2a cos C =2b +c ，所以有2sin cos 2sin sin A C B C =+， 在三角形中sin sin()B A C =+，所以有2sin cos 2sin cos 2cos sin sin A C A C A C C =++，整理得1cos 2A =-，因为(0,)A π∈，所以23A π=，由余弦定理可得2222cos 1644228a b c bc A =+-=++⨯=，所以a =222cos2a c b B ac +-====，所以在ABD △中，2cos AB B BD BD ===BD =所以AD =若选③，因为S =a 2-b 2-c 2），所以1sin cos 2ab C A =，由正弦定理可得sin sin sin sin cos A B C B C A =，整理得tan A = 因为(0,)A π∈，所以23A π=，由余弦定理可得2222cos 1644228a b c bc A =+-=++⨯=，所以a =222cos27a c b B ac +-====，所以在ABD △中，2cos AB B BD BD ===BD =所以AD =【点睛】方法点睛：关于此类问题的解题方法有： （1）根据自己对题中条件的理解，选择好条件；（2）利用正余弦定理对式子进行边角转化，结合三角形的内角和以及诱导公式求得角的大小；（3）从余弦定理入手求边长；（4）观察图形的特征，解三角形即可得结果.18．（1）28y x =（2）4π【分析】（1）根据抛物线的定义即可求出曲线的方程；（2）求出00(,)P x y 的坐标，利用PA 的斜率即可求出∠P AF 的大小. 【详解】(1）设M (x ，y )，圆M 的半径为r .点M 到点F (2，0)的距离等于M 到定直线2x =-的距离，根据抛物线的定义知，曲线C 是以F (2，0)为焦点，2x =-为准线的抛物线.故曲线C 的方程为28.y x = （2）设00(,)P x y ,由PA =，得22220000(2)2(2)x y x y ⎡⎤++=-+⎣⎦，又208y x =，解得02x =，故(2,4)P ±， 所以1PA k =±，故4PAF π∠=19．（1）证明见解析；（2）3. 【分析】（1）连接1B C 交1BC 于点O ，再连接OD ，利用中位线的性质可得出1//OD AB ，利用线面平行的判定定理可得出1//B A 平面1C BD ；（2）取BC 的中点E ，连接DE ，证明出DE ⊥平面11BB C C ，求出DE 的长以及11BB C 的面积，利用锥体的体积公式可求得三棱锥11B B C D -的体积. 【详解】（1）如下图所示，连接1B C 交1BC 于点O ，再连接OD ，则O 为1B C 的中点，O 、D 分别为1B C 、AC 的中点，则1//OD AB ，OD ⊂平面1C BD ，1AB ⊄平面1C BD ，因此，1//B A 平面1C BD ；（2）取BC 的中点E ，连接DE ，在直三棱柱111ABC A B C -中，1BB ⊥平面ABC ，AB平面ABC ，1∴⊥AB BB ，AB BC ⊥，1BB BC B =，AB ∴⊥平面11BB C C ，D 、E 分别为AC 、BC 的中点，则//DE AB 且1322DE AB ==， DE ∴⊥平面11BB C C ，1BB ⊥平面111A B C ，11B C ⊂平面111A B C ，111BB B C ∴⊥，且113BB AA ==，111111134622BB C S BB B C ∴=⋅=⨯⨯=△， 所以，三棱锥11B B C D -的体积为11111111363332B BCD D BB C BB C V V S DE --==⋅=⨯⨯=△. 【点睛】若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解，利用等体积法要结合线面垂直的条件或结论来确定的底面与高来求解.20．（1）02x y -+=或02x y --=（2）13m - 【分析】（1）根据圆心O 到直线AB 的距离列方程计算m 的值，得出直线AB 的方程；（2）求出以AB 为直径的圆D 的方程，令直线0x y --=与圆D 有公共点列出不等式，解出m 的范围． 【详解】（1）圆O 的半径为1，若ABC 是正三角形，则O 到AB 的距离为12，∴12=，m ∴=∴直线AB 的方程为0x y -+=或0x y -=．（2）直线AB 与圆O 有两个公共点，∴1<，即m <<，||AB == AB 的中垂线方程为y x =-，联立方程组0y x x y m =-⎧⎨-+=⎩可得22m x m y ⎧=-⎪⎪⎨⎪=⎪⎩， 即AB 的中点坐标为(2m D -，)2m ， ∴以AB 为直径的圆D 的方程为222()()1222m m m x y ++-=-，直线0x y --=上存在点P 满足·0AP BP =，∴直线0x y --=与圆D 有公共点，∴2|12m m m ----， 解得13m -． 【点睛】关键点点睛：本题考查直线与圆的位置关系，解题关键是利用圆心到直线的距离判定直线与圆的位置关系．本题中根据条件AB 为直径的圆D 的方程，然后直线0x y --=上存在点P 满足0AP BP =，转化为直线0x y --=与圆D 有公共点．考查了学生的运算求解能力，逻辑推理能力．属于中档题．21．（1）35；（2）13λ=. 【分析】（1）推导出PA ⊥平面ABCD ，然后以点A 为坐标原点，AB 、AD 、AP 所在直线分别为x 、y 、z 轴建立空间直角坐标系，利用空间向量法可求得直线DE 与平面ABE 所成角的正弦值；（2）求出平面ABE 和平面AEC 的法向量，利用空间向量法可得出关于实数λ的方程，结合01λ≤≤可求得实数λ的值.【详解】（1）平面PAB ⊥平面ABCD ，平面PAB ⋂平面ABCD AB =，PA AB ⊥，PA ⊂平面PAB ，PA ∴⊥平面ABCD ，AB AD ⊥，以点A 为坐标原点，AB 、AD 、AP 所在直线分别为x 、y 、z 轴建立空间直角坐标系，如下图所示：则()0,0,0A 、()2,0,0B 、()2,2,0C 、()0,0,4P 、()0,4,0D ， 当12λ=时，()1,1,2E ，则()1,3,2DE =-， 设平面ABE 的法向量为(),,m x y z =，()2,0,0AB =，()1,1,2AE =，由00m AB m AE ⎧⋅=⎨⋅=⎩，可得2020x x y z =⎧⎨++=⎩，得02x y z=⎧⎨=-⎩，取1z =-，则0x =，2y =， 所以，平面ABE 的一个法向量为()0,2,1m =-，cos ,14DE nDE n DE n ⋅<>===⋅ 因此，直线DE 与平面ABE ； （2）设平面AEC 的一个法向量为()111,,a x y z =，()0,0,4AP =，()2,2,0AC =， 由00a AP a AC ⎧⋅=⎨⋅=⎩，得11140220z x y =⎧⎨+=⎩，可得1110y x z =-⎧⎨=⎩，令11x =，则11y =-，10z =，所以，平面AEC 的一个法向量为()1,1,0a =-，设平面ABE 的一个法向量为()222,,b x y z =，()()2,2,42,2,4PE PC λλλλλ==-=-， ()()()0,0,42,2,42,2,44AE AP PE λλλλλλ=+=+-=-，()2,0,0AB =， 由00b AB b AE ⎧⋅=⎨⋅=⎩，得()22222022440x x y z λλλ=⎧⎨++-=⎩，令222y λ=-，则20x =，2z λ=， 所以，平面ABE 的一个法向量为()0,22,b λλ=-， 由于cos cos ,2a ba b a b θ⋅=<>===⋅⨯ 整理得23210λλ+-=，01λ≤≤，解得13λ=. 【点睛】 若利用空间向量求角，各类角都可以转化为向量的夹角来运算．（1）求两异面直线a 、b 的夹角θ，须求出它们的方向向量m 、n 的夹角，则cos cos ,m n θ=<>； （2）求直线l 与平面α所成的角θ，可先求出平面α的法向量n 与直线l 的方向向量m 的夹角，则sin cos ,m n θ=<>；（3）求二面角l αβ--的大小θ，可先求出两个平面的法向量1n 、2n 所成的角，则12cos cos ,n n θ=<>，并要根据图形确定所求二面角的平面角是锐角还是钝角.22．（1）22184x y +=（2）证明见解析 【分析】（1）根据条件联立方程组求出,a b 即可得出椭圆标准方程；（2）当PQ 斜率不存在时求出△PQN 的面积，当PQ 斜率存在时，设PQ 的方程为(0)y kx m m =+≠，联立方程组求出,N M 坐标，代入椭圆方程化简可得229214k m +=， 利用42OPQ S S PQ d ==⨯即可求解.【详解】（1）椭圆C 的左顶点(,0)a -，上顶点(0,)b .因为左顶点与上顶点的距离为=，化简得2212.a b +=①因为椭圆经过点(， 所以22421a b+=，② 由①②解得228,4a b ==或226,6a b ==（舍去)，所以椭圆C 的方程为22 1.84y x += （2）当PQ 斜率不存在时，N为(PQ ±方程为3x =±，易得PQ =此时1164.229S MN PQ =⨯⨯== 当PQ 斜率存在时，设PQ 的方程为(0)y kx m m =+≠， 联立22184y kx m x y =+⎧⎪⎨+=⎪⎩，得()()222124240k x kmx m +++-=， 由()()222(4)81240,km k m =-+->得2208 4.m k <<+ ()* 设()()1122,,,,P x y Q x y 则()2121222244,1212m km x x x x k k--+==++， 因此PQ 的中点M 为222,1212km m k k -⎛⎫ ⎪++⎝⎭由因为3,ON MO =所以2263,1212km m N k k -⎛⎫⎪++⎝⎭， 将点N 代入椭圆方程，得()()22222221891412412k m m k k +=++，化简得229214k m +=，符合(*）式. 记点О到直线l 的距离为d ,则1242OPQ S S PQ d x d ==⨯=-⨯==， 将229214k m +=代入，得264.94S m == 综上，PQN 的面积S 为定值649【点睛】 关键点点睛：本题考查求椭圆的标准方程，解题关键是找到关于,a b 的等量关系．本题中直线方程代入椭圆方程整理后应用韦达定理求出12x x +，然后求出M 表示出N ，由N 在椭圆上得到等量关系．利用三角形面积公式表示出面积，代入化简即可得定值.考查了学生的运算求解能力，逻辑推理能力．属于难题．。

江苏省南京航空航天大学附属高级中学2024届高三上学期12月月考数学试题一、单选题1．已知复数z 满足2i z z =+，则复数z 的虚部为（ ） A ．iB ．1C ．i -D ．1-2．已知集合,A U B U ⊆⊆.若()U A B =∅I ð，则（ ） A ．A B A =I B ．A B B =I C ．()U B A =∅I ðD ．A B U ⋃=3．已知直线1:10l x ay -+=，()2:11240l a x y ---=，则“4a =”是“12//l l ”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件4．粮食是关系国计民生的重要战略物资.如图为储备水稻的粮仓，中间部分可近似看作是圆柱，圆柱的底面直径为10m ，上、下两部分可以近似看作是完全相同的圆锥，圆柱的高是圆锥高的4倍，且这两个圆锥的顶点相距12m ，每立方米的空间大约可装0.75吨的水稻，则该粮仓最多可装水稻（ ）A ．175π吨B ．200π吨C ．225π吨D ．250π吨5．621()x x y y ⎛⎫-+ ⎪⎝⎭的展开式中42x y 的系数为（ ）A ．55B ．70-C ．65D ．25-6．古希腊数学家阿波罗尼奥斯所著的八册《圆锥曲线论（Conics ）》中，首次提出了圆锥曲线的光学性质，其中之一的内容为：“若点P 为椭圆上的一点，1F 、2F 为椭圆的两个焦点，则点P 处的切线平分12F PF ∠外角”.根据此信息回答下列问题：已知椭圆22:184x y C +=，O 为坐标原点，l 是点(P 处的切线，过左焦点1F 作l 的垂线，垂足为M ，则OM 为（ ）A ．B ．2C ．3D ．7．已知π0,2α⎛⎫∈ ⎪⎝⎭ππ32sin 334αα⎛⎫⎛⎫+-+=- ⎪ ⎪⎝⎭⎝⎭，则cos α=（ ）A ．13B ．12C D 8．已知在正方体1111ABCD A B C D -中，4AB =，点P ，Q ，T 分别在棱1BB ，1CC 和AB 上，且13B P =，11C Q =，3BT =，记平面PQT 与侧面11ADD A ，底面ABCD 的交线分别为m ，n ，则（ ）A ．mB ．mC ．nD ．n二、多选题9．已知向量,a b r r 满足22,0a b a a b a +=⋅+=r r r r r r ，且2a =r ，则（ ）A ．8b =rB ．0a b +=r r rC ．26a b -=r r D ．4a b ⋅=r r10．l 经过抛物线2:2(0)C y px p =>的焦点F ，与抛物线C 交于点,A B 两点（点A 在第一象限），与抛物线的准线交于点D ，若8AB =，则以下结论正确的是（ ）A ．32p =B ．6AF =C ．2BD BF =D ．F 为AD 中点11．在数列{}n a 中，()()*122110,1,2n n n a a a a a n ++===+∈N .则下列结论中正确的是（ ） A ．01n a ≤≤ B ．{}1n n a a +-是等比数列 C ．141615a a a <<D ．151614a a a <<12．已知函数()()e ,ln xf xg x x ==，其中e 为自然对数的底数.下列结论正确的是（ ）A ．函数()()e y f x g x =-的极值点为eB ．若,P Q 分别是曲线()y f x =和()y g x =上的动点，则PQC ．()()()0,,2x f x g x ∃∈+∞-≤D ．若()()()1f ax g x a x -≥-对任意的()0,x ∈+∞恒成立，则a 的最小值为1e三、填空题13．现有A ，B ，C ，D ，E 五人排成一列，其中A 与B 相邻，C 不排在两边，则共有种不同的排法（用具体数字作答）. 14．已知x ，y 取值如表：画散点图分析可知：y 与x 线性相关，且求得回归方程为ˆ1yx =+，则m =． 15．已知函数()πsin (0)6f x x ωω⎛⎫=-> ⎪⎝⎭在区间π,π2⎛⎫ ⎪⎝⎭内不存在对称轴，则ω的最大值是.16．四面体的棱长只能是1或3，但该四面体不是正四面体，则该四面体的体积最大值为.四、解答题17．如图,在ABC V 中,π4B ∠=,2AC AB =,D 为线段BC 上一点,π6CAD ∠=．(1)求CDAD的值; (2)当4=AD 时,求线段AC 的长．18．已知等差数列{}n a 前n 项和为n S （N n +∈），数列{}n b 是等比数列，13a =，11b =，2210b S +=，5232a b a -=.(1)求数列{}n a 和{}n b 的通项公式；(2)若2,,n n nn S c b n ⎧⎪=⎨⎪⎩为奇数为偶数，设数列{}n c 的前n 项和为n T ，求2n T .19．如图所示，在四棱锥P ABCD -中，PA ⊥底面ABCD ，2PA =，底面ABCD 为直角梯形，90BAD o ∠=，2AB =，1AD DC ==，N 是PB 的中点，点M ，Q 分别在线段PD 与AP 上，且DM MP λ=u u u u r u u u r ，AQ QP μ=u u ur u u u r .(1)当1λ=时，求平面MDN 与平面DNC 的夹角大小； (2)若//MQ 平面PBC ，证明：12μλ=+.20．甲、乙两人参加一场比赛，比赛采用五局三胜制（比赛最多进行五局，每局比赛都分出胜负，先胜三局者获胜，比赛结束）．由于心理因素，甲每局比赛获胜的概率会受到前一局比赛结果的影响：如果前一局比赛甲获胜，则下一局比赛甲获胜的概率为34；如果前一局比赛乙获胜，则下一局比赛甲获胜的概率为14．已知第一局比赛甲获胜的概率为35，事件n A 表示“第n 局比赛甲获胜”.(1)求第二局比赛甲获胜的概率；(2)证明：当()120P A A >时，112113322)()(|)|)((P A A A P A P A A A A A P =，并类比上述公式写出()1234P A A A A 的公式（不需要证明）；(3)求比赛结束时甲获胜两局的概率.21．已知函数()e ln(1)1(1)x f x a x a =-+-≥．(1)当e a =时，求曲线()y f x =在点(0,(0))f 处的切线与两坐标轴所围成三角形的面积； (2)若()f x 没有零点，求a 的取值范围．22．已知椭圆()2222:10x y E a b a b +=>>的左、右焦点分别为()11,0F -，()21,0F ，M 是椭圆上的一点，当1260F MF ∠=︒时，12F MF △(1)求椭圆E 的方程；(2)过右焦点2F 的直线l 与椭圆E 交于A ，B 两点，线段AB 的垂直平分线交直线l 于点P ，交直线2x =-于点Q ，求PQ AB的最小值.。