一维黎曼问题数值解与计算程序

The Exact Solution of One-Dimensional Ising ModelHere we want to describe the process of working out the one-dimensional Ising model which have an exact solution. During this process mathematics of the quantum mechanics would be used, some notion such as eigenvector would also be involved.In the first place, we introduce the definition of the Ising Model. Consider a two-dimensional square lattice composed of N = L ×L sites. Every site is occupied by a so-called spin, s i . In the magnetic material, the spins mean the magnetic dipoles positioned on the crystal structure lattice. In uniaxial magnetic materials, the magnetic dipole interactions constrain the spins to point parallel or anti-parallel along a given direction. Therefore, for simplicity, we assume that the spins can only be in one of two states, ether spin-up, s i = +1, or spin-down, s i = －1. By convention, the upwards direction is defined as positive direction. It is obvious that the spins interact with each other. A pair of parallel spins has an interaction energy of －J, while a pair of anti-parallel spins has an interaction energy of +J. We get the total internal interaction energywhere J ij are known as the coupling constants between spins s i and s j and the sum runs over all distinct pairs of spins. If we impose a uniform external field, H, which acts upon every spin, there would be an external energy. So the total energy of the entire model isIn the one-dimensional Ising model, the interaction energy of one spin s i has been simplified to a sum running over all distinct nearest-neighbor pairs. The new form of the total energy of 1D Ising model isIn addition, we apply periodic boundary conditions such that s N+1 = s i .According to equilibrium statistical mechanics, one can only measure any thermodynamic quantity of interest based on the partition function of the ensemble. The partition function can be written :where we have used the fact that for a periodic lattice. Now we introduce a 2×2 matrix :whose matrix elements are defined as∑-=ijj i ij int s s J E {}∑∑=--=+=N i i ij j i ij ext int s s H s s J E E E i 1{}∑∑==+--=N i i N i i i s s H s s J E i 111()()∑∑∑±==++±=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++=11111211N s N i i i i i s N s s H s Js exp H ,T Z β ∑∑=+=+=Ni i i N i i )s s (s 11121⎪⎪⎭⎫ ⎝⎛=---+)H J (J J )H J (e e e e ββββP ()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++=+++11121i i i i i i s s H s Js exp s s βPSo the partition function can be writtenwhereare the eigenvalues of the matrix P . To find the eigenvalues of P , we set the determinant to zero and get the solution :So with the help of the dirac mark, we define the operator P , the bra and the ket .We can simplify the process of solving the partition function to a process of solving eigenvalues of a 2×2 matrix. After getting the exact solution of the partition function, the thermodynamic quantities can be calculated. We can thoroughly understand the 1D Ising Model, especially its phase transition. ()∑∑±=±==11322111N s N s N s s s s s s H ,T Z P P P ∑±==1111s s s IP PIPI []N N N s N Tr s s -+±=+===∑λλP P 1111±λ()()()()()J exp H sinh H cosh J exp ββββλ42-+±=±()0=-I P λdet ()()()[]()()0222=--+-+-J exp J exp H exp H exp J exp ββλβββλs s。

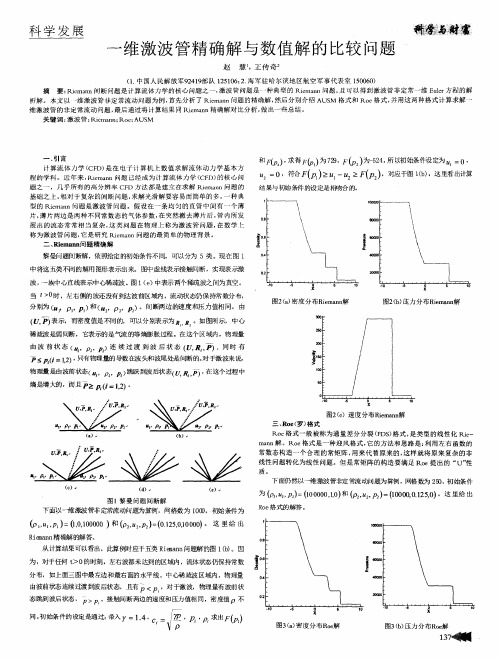
一维黎曼问题数值解与计算程序1000，计算总时间为0.4T =。

计算得到在0.4T =时刻的密度、速度和压力分布如图A.2（C 语言计算结果）和图A.3（Fortran77语言计算结果）所示。

采用两种不同语言编写程序所得到的计算结果完全吻合。

从图A.2和图A.3中可以发现，MacCormack 两步差分格式能很好地捕捉激波，计算得到的激波面很陡、很窄，计算激波精度是很高的。

采用带开关函数的前置人工滤波法能消除激波附近的非物理振荡，计算效果很好。

从图A.2和图A.3中可以看出通过激波后气体的密度、压力和速度都是增加的；在压力分布中存在第二个台阶，表明在这里存在一个接触间断，在接触间断两侧压力是有间断的，而密度和速度是相等的。

这个计算结果正确地反映了一维Riemann 问题的物理特性，并被激波管实验所验证。

A-2 一维Riemann 问题数值计算源程序图 A.2采用C 语言程序得到的一维问图 A.3采用Fortran77语言程序得到的一维1. C语言源程序// MacCormack1D.cpp : 定义控制台应用程序的入口点。

///*-----------------------------------------------------------------------------------------------------*利用MacCormack差分格式求解一维激波管问题（C语言版本）*-------------------------------------------------------------------------------------------------------*///#include "stdafx.h"#include <stdio.h>#include <stdlib.h>#include <math.h>#define GAMA 1.4//气体常数#define PI 3.141592654#define L 2.0//计算区域#define TT 0.4//总时间#define Sf 0.8//时间步长因子#define J 1000//网格数//全局变量double U[J+2][3],Uf[J+2][3],Ef[J+2][3];/*------------------------------------------------------- 计算时间步长入口: U，当前物理量，dx，网格宽度；返回: 时间步长。

黎曼问题解析解黎曼问题是数学上经典的非线性偏微分方程问题，它的解析解可以帮助研究者理解数学及其他领域的诸多问题，因此一直备受研究者的关注。

本文将从几个方面介绍黎曼问题解析解。

一、什么是黎曼问题？黎曼问题，也叫光滑的初值问题，是数学上一种经典的非线性偏微分方程问题。

它表示为如下的形式：$u_{t}+f(u)u_x=0$其中，$f(u)$为非线性函数，$u(x,0)$是初值，$x,t$为自变量。

二、黎曼问题的特点黎曼问题的初值是光滑的，即满足光滑的边界和一定的单值假设条件。

同时，黎曼问题的解存在唯一性，也就是说，只有一个解可以满足初值问题。

三、黎曼问题解析解的求解1、特征线法求解特征线法是求解黎曼问题的一种常用方法。

它的基本思想是沿着特征线求解，然后通过特征线上的解得到整个区域的解。

具体来说，就是先求解方程的一组特征线，$\frac{dt}{1}=\frac{dx}{f(u)}=\frac{du}{0}$通过积分可以得到，$\frac{du}{dx}=f(u),\frac{dx}{dt}=f(u)$又由于$u(x,0)=u_0(x)$，所以有$\frac{du}{dx}=f(u),u(x,0)=u_0(x)$这是一个一阶常微分方程，解之后就可以得到特征曲线。

由特征曲线可知，问题可以通过平移、反射、重叠等方式来求解。

2、古典解法求解古典解法是通过自相似、等比位移等线性变换的方式，将黎曼问题转化为带参数的一类常微分方程，然后通过分析常微分方程的本质特性，得到黎曼问题解析解。

3、Frobenius法求解Frobenius法是通过将初始点变成可表达的，然后求解它的发展方程，来求解黎曼问题的方法。

这个方法的关键在于，如何处理初值点，如何求解半平面级数，如何求解变换。

四、总结黎曼问题解析解的求解方法有很多，每种方法都有各自的特点和适用范围。

特征线法、古典解法和Frobenius法是比较常用的几种方法。

对于不同的问题，可以根据问题的特点，选择合适的方法去求解。

专题讲座5-一维问题1. 自由粒子问题自由粒子（处处()0V x =）。

在经典理论中它意味着等速运动，但是在量子力学中这个问题相当微妙。

定态薛定谔方程为:222,2d E m dxψψ-= 或者222,d k dx ψψ=- 其中k ≡用指数形式来表示其一般解：().ix ixx Ae Be ψ-=+ 对自由粒子没有边界条件去限制k 的取值（E 的取值）；自由粒子可以具有任何（正的）能量值。

加上标准的时间因子，exp(/)iEt - ，22(,).k k ik x t ik x t m m x t AeBe ⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭ψ=+ 我们知道，任何函数以特定的组合()x vt ±依赖变量x 和t （对某个常数v ）都代表一个具有固定波形的在x 方向传播的波。

波形上一个固定点（例如，最高点或最低点）对应着宗变量的一个固定值，使得变量x 和t 满足x vt ±=常数，或者 x v t =+常数 既然波形上的每一点都以同样的速度运动，波形的形状在转播的过程中是不改变的。

这样2.93式右边的第一项代表一个向右转播的波，而第二项代表一个向左的波(能量相同)。

既然这两个波的区别仅在于k 前面的正负号，我们也可以写作2()2(,),k i kx t mk x t Ae-ψ=并让k 可以取负值以包括向左传播的波：00 k k k >⇒⎧≡±⎨<⇒⎩向右传播，向左传播.显然，自由粒子的“定态”是传播着的波；它们的波长是2/k λπ=，按照德布罗意公式（1.39式）它们具有动量.p k = 这些波的速度(t 前面的系数除以x 前面的系数)是2kv m == 量子另一方面，一个具有能量2(1/2)E mv =（纯动能，既然势能0V =）的经典自由粒子的速度是2.v v ==量子经典 表面看来量子力学波的传播速度只有它所代表的粒子经典速度的一半！我们马上会回到这个佯谬−这里还有一个更严重的问题需要我们首先面对：这个波函数是不可归一化的。

专题讲座5-一维问题1. 自由粒子问题自由粒子（处处()0V x =）。

在经典理论中它意味着等速运动，但是在量子力学中这个问题相当微妙。

定态薛定谔方程为:222,2d E m dxψψ-= 或者222,d k dx ψψ=- 其中k ≡用指数形式来表示其一般解：().ix ixx Ae Be ψ-=+ 对自由粒子没有边界条件去限制k 的取值（E 的取值）；自由粒子可以具有任何（正的）能量值。

加上标准的时间因子，exp(/)iEt - ，22(,).k k ik x t ik x t m m x t AeBe ⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭ψ=+ 我们知道，任何函数以特定的组合()x vt ±依赖变量x 和t （对某个常数v ）都代表一个具有固定波形的在x 方向传播的波。

波形上一个固定点（例如，最高点或最低点）对应着宗变量的一个固定值，使得变量x 和t 满足x vt ±=常数，或者 x v t =+常数 既然波形上的每一点都以同样的速度运动，波形的形状在转播的过程中是不改变的。

这样2.93式右边的第一项代表一个向右转播的波，而第二项代表一个向左的波(能量相同)。

既然这两个波的区别仅在于k 前面的正负号，我们也可以写作2()2(,),k i kx t mk x t Ae-ψ=并让k 可以取负值以包括向左传播的波：00 k k k >⇒⎧≡±⎨<⇒⎩向右传播，向左传播.显然，自由粒子的“定态”是传播着的波；它们的波长是2/k λπ=，按照德布罗意公式（1.39式）它们具有动量.p k = 这些波的速度(t 前面的系数除以x 前面的系数)是2kv m == 量子另一方面，一个具有能量2(1/2)E mv =（纯动能，既然势能0V =）的经典自由粒子的速度是2.v v ==量子经典 表面看来量子力学波的传播速度只有它所代表的粒子经典速度的一半！我们马上会回到这个佯谬−这里还有一个更严重的问题需要我们首先面对：这个波函数是不可归一化的。

Riemann问题精确解及程序实现在流体力学和计算流体动力学中，Riemann问题是一个经典的数学物理问题，对于理解激波、稀疏波和激波-叠加问题等都有重要意义。

Riemann问题的精确解是指在一个特定的初始条件下，精确地求解出Riemann问题得到的解析解。

对于Riemann问题的精确解以及在计算流体动力学中的程序实现，我们将深入探讨并提供一些观点和思考。

一、Riemann问题的基本概念1. Riemann问题的基本描述Riemann问题最初由德国数学家Bernhard Riemann提出，是一类包含一个跨越一维空间的虚线和其两侧分别是不同状态的初始值问题。

它被广泛地运用在气体动力学、流体力学、等离子体物理、弹性力学等领域。

Riemann问题的基本描述是求解一组非线性偏微分方程组在时间和空间上的解析解，问题的初值包含两个不同的宏观态。

这个问题在数值计算和模拟中具有重要意义。

2. Riemann问题的物理意义Riemann问题是一维激波的基本问题，对于理解一维激波和稀疏波结构以及它们在多维情况下的相互作用有着重要的物理意义。

它的解可以帮助我们更好地理解气体动力学、流体力学等领域中的复杂现象。

二、Riemann问题的精确解1. 常见的Riemann问题常见的Riemann问题包括Euler方程、Navier-Stokes方程等，它们描述了流体的运动、压力、密度等物理量。

对于这些问题，我们可以使用不同的数值方法来求解它们的精确解，如Lax-Friedrichs方法、Roe方法等。

2. 求解Riemann问题的精确解对于一维的Riemann问题，可以通过计算它的特征线和跃度条件来求解其精确解。

在特征线上，可以得到一维激波的解，而跃度条件则用来确定激波的速度和压力等物理量。

这些方法对于理解和解决Riemann问题非常重要。

三、Riemann问题的程序实现1. 基于数值方法的程序实现在计算流体动力学中，为了求解Riemann问题的精确解，可以使用基于数值方法的程序实现。

一维黎曼问题是流体动力学中一个经典的数学模型，描述了两个不同状态之间的激波和稀疏波的相互作用。

Roe格式是一种数值求解一维黎曼问题的格式，用于求解非线性双曲型偏微分方程，例如Euler方程，它描述了可压缩流体的运动。

Roe格式的基本思想是在守恒形式的方程中引入线性波的概念，通过一些近似的手段来计算这些波的速度和通量。

下面是一维黎曼问题Roe格式的详细解释：1.守恒形式的方程：一维黎曼问题通常使用守恒形式的方程，如Euler方程，它们描述了质量、动量和能量的守恒。

2.状态重构： Roe格式首先对两个相邻状态进行重构。

假设左侧状态为U L，右侧状态为U R，则通过一些线性插值或重构方法（通常是Roe平均），可以得到一个平均状态U avg。

3.Roe平均： Roe平均是一种通过左右两个状态的差值来计算平均状态的方法，其具体形式为：U avg=√ρR U R√ρL U L√ρ+√ρ这里ρ是密度。

4.特征分解：通过对平均状态U avg的雅可比矩阵进行特征分解，得到特征值和对应的特征向量。

这些特征值和特征向量代表了系统中传播的线性波。

5.Roe通量：根据得到的特征值和特征向量，可以计算Roe格式的数值通量。

这通常涉及将特征分解应用于左右两侧的守恒变量，然后计算通过每个波传播的通量。

6.数值通量更新：最后，通过将计算得到的数值通量应用到空间离散的格式中，例如Godunov方法，从而更新守恒变量的时间步进。

总的来说，Roe格式是一种使用了特征分解和平均状态的数值格式，适用于一维黎曼问题的求解。

这个格式的优点之一是相对简单且有效，特别适用于高速激波的问题。

一维Riemann 问题数值解与计算程序一维Riemann 问题，即激波管问题，是一个典型的一维可压缩无黏气体动力学问题，并有 解析解。

对它采用二阶精度MacCormack 两步差分格式进行数值求解。

同时，为了初学者入门和练习方便,这里给出了用C 语言和Fortran77编写的计算一维Riemann 问题的计算程序，供大家学习参考。

A-1利用MacCormack 两步差分格式求解一维Riemann 问题1.一维Riemann 问题一维Riemann 问题实际上就是激波管问题。

激波管是一根两端封闭、内部充满气体的直管，如图A.1所示。

在直管中由一薄膜将激波管隔开，在薄膜两侧充有均匀理想气体（可以是同一种气体，也可以是不同种气体），薄膜两侧气体的压力、密度不同。

当0≤t 时，气体处于静止状态。

当0t =时，薄膜瞬时突然破裂，气体从高压端冲向低压端，同时在管内形成激波、稀疏波和接触间断等复杂波系。

2.基本方程组、初始条件和边界条件设气体是理想气体。

一维Riemann 问题在数学上可以用一维可压缩无黏气体Euler 方程组来描述。

在直角坐标系下量纲为一的一维Euler 方程组为：,11x t x∂∂+=-≤≤∂∂0u f(A.1) 其中 2,()u u u p E E p u ρρρρ⎛⎫⎛⎫ ⎪ ⎪==+ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭u f (A.2)这里ρ、u 、p 、E 分别是流体的密度、速度、压力和单位体积总能。

理想气体状态方程：()()()221112p e E u v γργρ⎡⎤=-=--+⎢⎥⎣⎦（A.3）初始条件：1111,0,1u p ρ===；2220.125,0,0.1u p ρ===。

图A.1 激波管问题示意图边界条件：1x =-和1x =处为自由输出条件，01u u =,1N N u u -=。

3.二阶精度MacCormack 差分格式MacCormack 两步差分格式：()121111122211122n n n njj j j n n n n n jj j j j r r +-+++++=--⎛⎫⎛⎫=+-- ⎪ ⎪⎝⎭⎝⎭u u f f uu u f f (A.4)其中tr x∆=∆。