《平方根与立方根》课件

数
0
0
负数
没有
立方根
一个正的 立方根
0 一个负的 立方根
练习：
一、判断正误 ⑴ 0.0009 0.03 。 ⑵ 9是的(－9)2算术平方根。 ⑶ 361 的平方根是±19。 ⑷有理数一定有立方根。 ⑸若某数的立方根是它本身，那么 这个数一定是±1或0。 ⑹一个数的立方根总比这个数的平 方根要小。
例九：已知：x2=64, x =-x, 求:
的值
x+1
十 ：若x、y为实数,y＜ x-1 +
1-x +
1 2
化简: 1-y . y-1
十一
已知x=(
-2a 4+a
-
a - 3 + 3- a
)2013
3-a
求:x的个位数字
⑴ 121
⑵ 232
⑶ (-4)2
⑷0
⑸ -25
平方根的情况: ⑴一个正数的平方根有两个, 它们是互为相反数; ⑵ 0的平方根只有一个, 就是它本身0; ⑶负数没有平方根.
立方根的概念：
如果一个数的立方等于a，那么这个 数就叫做a的立方根。 即：若x3=a，则x叫做a的立方根
立方根的表示：3 a （为任意有理数）
一、什么叫平方根？什么叫算术平 方根？
如果一个数的平方等于a ，那么这 个数就叫做a的平方根。
即：若x2=a，则x叫做a的平方根。
正数a的正的平方根叫做a的算术平 方根；零的算术平方根是零。
二、平方根和算术平方根的表示方法： 平方根： ± a （a≥0）
算术平方根： a （a≥0）
想一想
下列各数的平方根会是怎样的?
正数有立方根吗？如果有，有几个? 负数呢？ 零呢？

行异动后的薪资； 2、教师考评涨薪期内： 每月考受处罚一次，对应考评优质课时指
标加50小时；每退费一人次，对应考评优质课时指标加50小时；每被替 换一次，对应考评优质课时指标加50小时；每被投诉一次，对应考评优 质课时指标加50小时；
3、续推30小时计为1人次;4）考评期内必须完成相应公函的研发任 务（具体见公函），否则取消考评资格
①一个正数的立方根为正； ②一个负数的立方根为负； ③零的立方根是零； 3、立方根的表示：立方根的记号：（读作：三次根号a），a称为被开方数，“3” 称为根指数。
2、小班课： 1-2：课时费为标准课时费*1.2，教师优质课时计为1h； 1-3：课时费为标准课时费*1.3，教师优质课时计为1h； 以此类推。校区消课小时数为一对多课程中所有学生消课小时数。
三、平方根与算数平方根的表示
1、平方根±（读作：正负根号a）；算术平方根（读作根号a）即：“±”表示a的 平方根，或者表示求a的平方根； 2、“”表示a的算术平方根，或者表示求a的算术平方根。
四、立方根
1、立方根的定义：如果一个数的立方等于a，那么这个数叫做a的立方根。（也 叫做三次方根）即：若x3=a，则x叫做a的立方根。 2、立方根的性质
2.考评条件
1级升2级 2级升3级 3级升4级 4级升5级
涨底薪一档或涨课补一级条件 460小时优质课时+4单试听成功+1单续费+1单推荐+平均提分率不低于80% 580小时优质课时+4单试听成功+2单续费+2单推荐+平均提分率不低于85% 700小时优质课时+4单试听成功+3单续费+3单推荐+平均提分率不低于85% 820小时优质课时+4单试听成功+4单续费+4单推荐+平均提分率不低于90%

宫妇左右莫不私王 朝廷之臣莫不畏王
四境之内莫不有 求于王
“ ——
《 古 文 观 止 》
语 破 之 ， 快 哉 ！ ”
关 头 ， 从 闺 房 小
臣 谄 君 蔽 ， 兴 亡
参 出 微 理 。 千 古
详 勘 。 正 欲 于 此
徐 公 之 美 ， 细 细
邹 忌 将 己 之 美 、
思考问题：
从文中看，齐威王最终能使 齐国“战胜于朝廷”，达到 “大治”的原因是什么？这给 我们带来什么启示？请结合你 的生活体验，简要谈谈你的看 法。
( )
四：小结 1：为什么要学习数的开方？ 2：开方与什么互为逆运算？ 3：平方根，算术平方根，立方根的概念和性质
五：作 业 练习册
导入新课
“以铜为镜，可以正衣冠； 以史为镜，可以知兴亡； 以人为镜，可以明得失。”
唐·魏征
《战国策》是一部重要的历史著作，也 是一部重要的散文集。作者已不可考， 最初有《国策》、《国事》、《短长》 等名称，经过汉代刘向整理编辑，始定 为《战国策》。全书共33篇，分国别编 辑。
2.君子之过，如日月之食也。过也， 人皆见之，及其更也，人皆仰之。 （《论语》）
3.良药苦口利于病，忠言逆耳利于行。 （孔子家语）
4.信言不美，美言不信。（老子）
解释下列蓝色的词 词类活用
1、吾妻之美我 认为……美，形容词意动用 者，私我也。 法 偏爱，形容词作动词。
2、能面刺寡人 之过者
3、受上赏
《战国策》的内容，主要记载战国时期 各国谋臣策士游说诸侯或进行谋议论辩 时的政治主张和纵横捭阖、尔虞我诈的 故事，也记叙了一些义士豪侠不畏强暴、 勇于斗争的行为。
《战国策》长于议论和叙事，文笔流畅， 生动活泼，在我国散文史上具有重要的 地位。

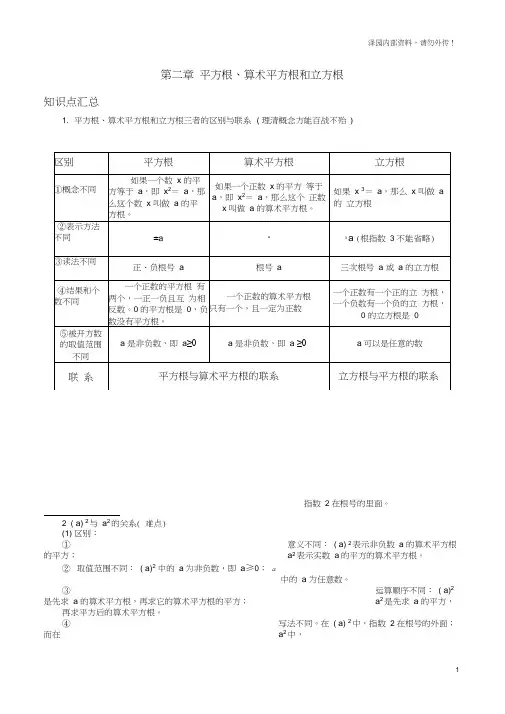
第二章平方根、算术平方根和立方根知识点汇总1. 平方根、算术平方根和立方根三者的区别与联系( 理清概念方能百战不殆)指数 2 在根号的里面。

2 ( a) 2与a2的关系( 难点)(1) 区别：①意义不同：( a) 2表示非负数 a 的算术平方根的平方；a2表示实数a的平方的算术平方根。

②取值范围不同：( a)2中的a为非负数，即a≥0；a2中的 a 为任意数。

③运算顺序不同：( a)2是先求 a 的算术平方根，再求它的算术平方根的平方；a2是先求 a 的平方，再求平方后的算术平方根。

④写法不同。

在( a) 2中，指数 2 在根号的外面；而在a2中，⑤运算结果不同：(a)2＝a(a≥0) ； a ＝| a|＝a，a≥0，－a，a<0.（2） 联系：①在运算时，都有平方和开平方的运算。

②两式运算的结果都是非负数，即 ≥0. ③仅当 a ≥0时，有 （ a ）2＝ a 2 。

3. 立方根的化简公式： 3 a 3 ＝a ；（3 a ）3＝a ； 3 a ＝－ 3 a( a ) 2≥ 0， a 21．．选择2014·南京） 8 的平方根是（ A ． 4B ．±42． （2014 。

东营 ） 的平方根是（ A ．±3 B ．3 3． 2014?连云港） 计算 A ． ﹣3 B ． 4.（2014。

厦门） 4 的算术平方根是（ A ． 16 B ．5．下列计算中，正确的是（ 典型题精选）C ．的结果是（±9 C ． C ． D ．D ．9﹣9 D ． ﹣2 D ． ±2 3 2 6 A.a · a =a B. ( π -3.14 )o =1 C. (13)1) 2C ．( ab ) 3 D. 93 6.（2014 年湖北荆门 ）下列运算正确的是 A ．3﹣1=﹣3 B ． =±3 7. 下列说法错误的是（ ） A ．5是 25 的算术平方根 C ．（－4）2 的平方根是－ 4 8．如果 x 是 0.01的算术平方根，则 A ． 0.000 1 C ．0.1 9.下 列说法中，正确的是（ ） A. 一个有理数的平 方根有两个，B. 一个有理数的 立方根，不是正数就是负数C.负数没有立方根D.如果一个数的立方根是这个数本身，那么这个数一定是－ 10. 下列各式中，无意义的是（ ） x ＝（ B ． D ． 36 =a b D ．a 6 2 ÷a =a A. 32 B ．1 是 1 的一个平方根D ．0 的平方根与算术平方根都是 ）±0.000 1±0.1 它们互为相反数 1， 0，1 B. 3 ( 3)3 C. ( 3)2 D. 10 3 绝对值与算术平方根的非负性）11. 若 a,b 为实数，且满足 |a －2|+ b 2 =0，则 b －a 的值为（ ）A ．2B ．0C ．－ 2D ．以上都不对平方与算术平方根的非负性）12.（2014·福州） 若（m-1）2+ n 2 ＝0，则 m ＋ n 的值是（ A ．－ 1 B ． 0 C ．1 13. 有一个数值转换器，原理如图所示：当输入的D ．2x 错误！未找到引用源。

根”。
（2）个数不同：一个正数有两个平方根，而一个
正数的算术平方根只有一个。
（3）表示方法不同：正数a的算术平方根表示
第9页/共32页
立方根：
1. 定义:
一般地，如果一个数x的立方等于a，即x3=a， 那么这个数x就叫做a的立方根．(也叫做三次方 根) 。
2.表示方法：
第10页/共32页
什么叫做开平方？那开立方呢？
无理数： 无限不循环小数
含有 ～ 的数
有规律但不循环的数
第25页/共32页
按性质分类： 实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
负实数
正实数
0
第26页/共32页
你能在数轴上找到表示 的点吗？
2
小结：
有理数可以用数轴上的点表示，无理数也可以用数轴上的点 表示.
每一个无理数都能在数轴上表示出来. 数轴上的点有些表示有理数，有些表示无理数. 每一个实数都可以用数轴上的一个点来表示；反过来， 数轴上的每一点都表示一个实数。即实数和数轴上的 点是一一对应的。
第21页/共32页
思考：
2 介于哪两个整数之间？你是根据什么考虑的？
A
1
2
B 4D
1
2
2C
1.42 __<__( 2)2 __<__1.52
1.4 ___<_ 2 __<__1.5
1.412 _<___( 2)2 __<__1.42 2
1.41 ___<_ 2 __<__1.42
1.414 2 _<___( 2)2 _<___1.415 2
第28页/共32页

做二次方根）。记为“ a ”读作“正、负
根号a”
2
立方根的定义. 一般地，如果一个数的立方等于a，这个
数就叫做a的立方根(也叫做三次方根). 用式子表示，如果X3 =a，那么X叫做a的立方根.
数a的立方根用符号“3 a ”表示,读作“三次根号a
其中a是被开方数,3是根指数(注意:根指数3不能省 略).
算术平方根
定义：如果一个正数x的平方等于a，即 x2
=a ，那么这个正数x就叫做a的算术平方
根，记为“ 做被开方数
a
”，读作“ 根号 a ”。a叫
规定：0的算术平方根是0,即 0 0
非负数
a ≥0 （a≥0）
算术平方根具有双重非负性
1
平方根定义
一般的，如果一个数X的平方等于a，即
x2=a那么这个数X叫做a的平方根（也叫
3
区别
你知道算术平方根、平方根、立方根联 系和区别吗？
算术平方根
平方根
立方根
表示方法
a的取值
正数
性
0
质
负数
开 方 是本身
a ≠ a
a≥ 0
a≥ 0
3a a是任何数
正数（一个） 互为相反数（两个） 正数（一个）
0 没有
0 没有
0 负数（一个）
求一个数的平方根 求一个数的立方根
的运算叫开平方 的运算叫开立方
10
3.说出下列各式的值：
（1） - 81 9 （4） 3 125 5
（2） （-25）2 2 5 （5）-3 0.027 0 .3
（ 3） 25 36
5 （6） - 3 125 5
6
82
11
不 要 遗 漏 哦！

类似平方根的讨论， 思考：正数、负数、0的算术平方根各有几个？ 正数的算术平方根是一个正数，0的算术平方根 还是0，负数没有算术平方根.
例如：16的平方根是4和-4，其中4是16的算 术平方根.
算术平方根的性质
非负数 a 0
a的算术平方根 a
非负数 a 0
算术平方根具有双重非负性
典例精析
例3 分别求下列各数的算术平方根：
第6章 实数
6.1 平方根、立方根 第1课时
学习目标
1.了解平方根及算术平方根的概念，会用根号表示 一个数的算术平方根;(重点)
2.会求非负数的平方根与算术平方根．(重点、难 点)
3.会用计算器求一个数的平方根；
视察与思考
某家庭在装修儿童房时需铺地垫10.8m2，刚好
用去正方形的地垫30块. 你能算出每块地垫的边长
解 (1) 依次按键 3136 ， 显示：56． ∴ 3136 56 ．
(2) 依次按键 2 ， 显示：1.414213562． ∴ 2 1.414 ．
典例精析
例5 随着“神舟”十号的升空，中国人又走出了探索宇宙 的一 大步，但是你知道吗，要想环绕着地球旋转，飞船的速度必须 到达“第一宇宙速度”，其计算公式是 v gR（单位：km/s， 其中g=0.0098km/s2，为重力加速度，R为6370km，为地球半 径），请你求出第一宇宙速度的值（结果精确到0.01）.
我们把正数a的正平方根 a 叫作a的算术平方根. 换句话说， 如果正数x满足:x2=a ，那么x叫作a的算术平方根.
a的算术平方根 记作 a
练一练: 判断下列说法是否正确.
①25的算术平方根是5 ②25的平方根是5
（ √ ）；
（ ）；

平方根的减法运算
平方根的乘法运算
平方根的除法运算
对于任何正实数a和b，有√a √b = √(a-b)。
对于任何正实数a和b，有√a * √b = √(ab)。
对于任何正实数a和b（b≠0） ，有√a / √b = √(a/b)。
02
立方根的定义与性质
立方根的基本定义
80%
立方根的概念
若一个数的三次方等于a，则这 个数称为a的立方根。
开方与加减法的关系
当被开方数的小数点向右移动一位，则其立方根的小数点相应地向右移 动三位；当被开方数的小数点向左移动一位，则其立方根的小数点相应 地向左移动三位。
03
平方根与立方根的应用
在数学中的应用
平方根用于求解非负数平方的问题，例如计算一个数的平方或求 解一元二次方程的实数根。
立方根用于求解一个数的立方的问题，例如计算一个数的立方或 求解一元三次方程的实数根。
详细描述
配方法适用于求解任意实数的平方根。首先，将被开方数进行配方，使其成为一 个完全平方数的形式，然后利用开平方的公式进行计算。例如，求√25的值，可 以先将25写成(5×5)的形式，即√25=√(5×5)=5。
因式分解法
总结词
因式分解法是一种通过因式分解来求解平方根的方法。
详细描述
因式分解法适用于求解一些特殊数的平方根。首先，将被开方数进行因式分解，将其写成两个相同因数的乘积形 式，然后利用开平方的公式进行计算。例如，求√8的值，可以先将8写成(2×2×2)的形式，即 √8=√(2×2×2)=2√2。
运算性质
立方根具有一些运算性质，例 如√[3]a^3=a， √[3](a+b)^3=a+b等。
立方根的运算规则

1 4
（1）、说说你对平方根的理解？ （2）、开平方运算与平方运算有 什么联系？有什么区别？
求一个数的平方根的运算，叫做开平方 （extraction of square root)
开平方与平方互为逆运算，可以利用平 方来检验开方是否正确
观察下面的式子: ① 12=1, (-1)2=1 ② 0.52=0.25, (-0.5)2=0.25 1 1 2 1 1 2 ③ (3 ) = , (-1 1 ) = 3 9 9 3939 (1) 请你写出一个与上面式子类同的式子; (2)你发现了什么结论?
§2.3 平方根
小明到装饰城购买瓷砖，老板给了 他一块面积为4dm2的正方形瓷砖， 聪明的你能告诉小明这块瓷砖的边 长吗？
平方根的定义
一般地,如果一个数的平方等于a,那么 这个数叫做a的平方根(square root),也 称为二次方根.也就是说,如果x2=a,那 么x叫做a的平方根.
友情提醒

平方根的性质
一个正数a有两个平方根,它们互为相反数. 0只有一个平方根，它是0本身； 负数没有平方根
求下列各数的平方根: (1)25 ; (2) 16 (3)15; (4)(-2)2 81 解:(1)因为(±5 )2=25,所以25的平方根是± 5
即±
4 2 (2)因为(± ) = 4 9 即± 9 = ±
一个正数a有两个平方根,它们互为相反数. 正数a的正的平方根,记作“ a ” 正数a的负的平方根,记作“- a ” 这两个平方根合在一起记作“± a ”
想一想
在下列各括号中,能填写适当的数使等式成立吗? 如果能够,请填写;如果不能,请说明理由,并与 同学交流. ① ( )2=9 ;( )2=25 ; ( )2=49 ② ( )2=2 ; ( )2=3 ; ( )2=0 ③ ( )2=-2

第1讲《平方根、立方根与非负数》知识点概述1、平方根(1)定义：如果一个数的平方等于a ，这个数就叫做a 的平方根（或二次方根）。

即：如果x 2=a ，那么x 就叫做a 的平方根。

(2)平方根的表示法：一个正数a 的正的平方根，用符号“a ”表示，读作“根号a ”; 正数a 的负平方根，表示为－a ，读作“负根号a ”。

(3)正数、零、负数的平方根：正数a 的平方根有两个，它们互为相反数，可以表示为±a ； 零的平方根有一个，仍是零； 负数没有平方根. 2.算术平方根(1)定义：一个正数a 的正的平方根，叫做a 的算术平方根，记作a ；0的算术平方根是0. (2)对a 的理解：①()2a =a ； ②a ≥0.(3)对记号a ，－a ，±a 的理解： ①a 表示非负数（a ≥0）; ②－a 表示a 的算术平方根的相反数; ③±a 表示a 的平方根; ④a<0时，a ，－a ，±a 都没有意义.3、如果一个数的立方等于a ，那么这个数叫做a 的立方根。

即：如果x 3=a ，那么x 就叫做a 的立方根。

一个数a 的立方根，用符号“3a ”表示，读作“三次根号a ”。

注：任何数（正数、负数或零）都有一个立方根例题讲解例1、下列语句正确的是（ ）A ．- a 没有平方根B ．-5是 – 25的平方根C ．( - 3)2 的平方根为-3D ．-15是225的平方根例2、94的平方根是＿＿；算术平方根是 ；0.04的算术平方根是 。

例3、求下列各数的立方根： （1）512 （2）－0.027 （3）－12564 （4）278 （5）－125 （6）－0.008．例4、求下列各数的平方根：（1）49 （2）8136 （3）232⎪⎭⎫ ⎝⎛-例5、求下列各数的算术平方根： （1）196（2）197（3）16例6、填空：（1）当x 时，3+x 有意义。

（2）如果a 的平方根是±3，则a = .（3）如果一个正数的平方根是a+3与2a －15，那么这个正数是（4的平方根是 ；算术平方根是___________ （5）若a 2=16，则a=________；若38a =，则a =（610y +=，则x 2+y 2=____________（7）代数式－3___________，这时a 与b 的关系是_________ （8）若2(2)289x +=，则x = ； 若24250x -=，则x =（9= 例7、下列命题中，正确的个数有（ ）(1)1的平方根是1; (2)1是1的平方根; (3)（－1）2的平方根是－1; (4)一个数的平方根等于它的算术平方根，这个数是0. A 、1 B 、2 C 、3 D 、4例8、要使2a -有意义，则a 的值为（ ）A 、a>0B 、a<0C 、a≥0D 、a=0例9、一个自然数的算术平方根是a ，则与这个自然数相邻的后继自然数的平方根是（ ） A 、a+1 B 、a 2+1C 、±1+aD 、±12+a例10、当x 为何值时，下列各式在实数范围内有意义.(1)32+x ； (2)x 31-； (3)2)5(-x ； （4）21+x非负数的相关知识1、非负数的意义：在实数集合里，正数和零称为非负数.a 是非负数，可记作a ≥0,读作a 大于或等于零，即a 不小于零. 2、 初中学过的几种非负数：⑴ 实数的绝对值是非负数. 若a 是实数，则a ≥0.⑵ 实数的偶数次幂是非负数. 若a 是实数，则a 2n ≥0（n 是正整数）.⑶ 算术平方根是非负数，且被开方数也是非负数。

平方根与立方根的区别： 表示方法
被开方数 性质
平方根
非负数
立方根
3
任意实数
正数的平方根 有两个；0的 平方根是0； 负数没有平方 根。
正数的立方根 是正数； 0的立方根是0； 负数的立方根 是负数
平方根：
立方根:
0.01 0.001 0.1 (1)0.0001 2 6 36 8 (2) 3 7 27 49 0 0 (3)0 0 3 2 (4) 4 4 4 4
（1）互为相反数的数的立方根也互为相反数 （2）立方根是它本身的数只有零 （3）平方根是它本身的数只有零 6、如果要制作一个立方体，使它的体积是已 知立方体体积的27倍，那么它的棱长应是已 知立方体的棱长的几倍？
例3． 解方程： (1)x3=0.125；
解：(1)x3=0.125 x=0.5．
(2)3(x-4)3-1536=0．
我们把括号里的±3叫做9的平方根（二次方根）。
同理：若(
3 ) 27
3
这也是已知指数和幂求底数的运算，仍然叫 做开方运算
我们把括号里的 3 叫做27的立方根（三次方根）
一般地，如果 x a ，那么 x 叫 a 的 立方根，也叫做 a 的三次方根 ， a 叫 x 的立 方数
3
数
a 的立方根用符号
(5) 16
2
64 2
从上面的例题可知：
3
27 3
3
27 3
3
由此可得出： 3
27 27
也就是把根号里的“负号”直接从根号里 面提到了根号“外面” 。
特别注意：平方根不能这样哟！
由此得出求一个负数的立方根的一般方法：
3

第2讲平方根与立方根⎧⎪⎪⎪⎨⎪⎪⎪⎩概念性质算术平方根、平方根、立方根化简运算综合1． 什么是相交线？相交线模块学习了哪些概念？2． 平行线有哪些性质？怎么判定两条直线平行？3． 平行线相关求角度的题型应如何做辅助线？前章回顾知识网络图中考说明2.1定义及性质一．算术平方根1．概念：一般地，如果一个正数x的平方等于a，即0a≥，那么这个正数x叫做a的算术平方根. 2．表示方法：一个非负数a a”，a叫做被开方数.3．规定：0的算术平方根是0.4．特别的，一个正数的算术平方根仍是正数，负数没有算术平方根.5．0≥（0a≥）6．算术平方根的运算（10a≥，0b≥）；（2=（0a≥，0b>）7．常见数的平方与算术平方根二．1．概念：一般地，如果一个数的平方等于a，那么这个数叫做的平方根(或二次方根)．这就是说，若0a≥，则x就叫做a的平方根．2．表示方法：一个非负数a的平方根记为为“”，读作“正负根号a”．3．①一个正数a有两个互为相反数的平方根，其中正的平方根叫做a的算术平方根.②0有一个平方根，就是0.③负数没有平方根．4．平方根的计算：求一个非负数的平方根的运算，叫做开平方．（1）开平方与加、减、乘、除、乘方一样，是一种运算，它的运算结果是平方根（2）开平方与平方是互逆运算，可以通过平方运算来求一个数的平方根或算术平方根，以及检验一个数概念辨析是不是另一个数的平方根或算术平方根．（3）平方与开平方的运算：①2a=（0a≥）；(0)0 (0)(0)a aa aa a>⎧⎪==⎨⎪-<⎩a=可用口诀“出门摘帽带夹板”帮助记忆.三．立方根1．概念：如果一个数的立方等于a，那么这个数叫做a的立方根（或三次方根）.这就是说，若3,x a=则x就叫做a的立方根．2．表示方法：一个数a，读作“三次根号a”，其中a叫做被开方数，“3”叫做根指数，不能省略．注意：前面学习的其实省略了根指数“2”3．任何一个数都有立方根，且只有一个立方根.正数的立方根为正数，负数的立方根为负数，0的立方根为0．4．立方根的计算：求一个数的立方根的运算，叫做开立方，开立方与立方是互逆运算.（1）可以通过立方运算来求一个数的立方根，以及检验一个数是不是另一个数的立方根．（2）立方与开立方的运算①3a=；②a=5．常见数的立方与立方根四．平方根与立方根1．区别：（1）根指数不同：平方根的根指数是2，通常省略不写；立方根的根指数是3，却不能省略．（2）被开方数取值范围不同：平方根中被开方数必须是非负数；立方根中被开方数可以为任何数．（3）平方的结果不同：平方根的结果除0之外，还有两个互为相反数的结果；立方根的结果只有一个．（4）平方根等于本身的数是0；算术平方根等于它本身的数是0，1； 立方根等于它本身的数是0，1，1-； 2． 联系：（1） 平方根与立方根相等的数是0．（2） 平方根与立方根都是与乘方运算互为逆运算．【例1】 判断题：（1( )（2）2a 的算术平方根是a ． ( ) （3）2a -没有算术平方根．( )（4）如果两个非负数相等，那么他们各自的算术平方根也相等． ( )【例2】 判断题：（1） 若264x =，则8x =±． ( )（2）8±．( )（3） 6-是()26-的平方根 ( ) （4） 若两个数平方后相等，则这两个数也一定相等． ( )（5） 如果一个数的平方根存在，那么必有两个，且互为相反数． ( ) （6） 2a -没有平方根．( )例题精讲【例3】 判断题：（1） 64的立方根是4±． ( ) （2） 12-是16-的立方根．( ) （3）x ．( ) （4） 互为相反数的两个数的立方根互为相反数．( )【例4】 下列说法正确的是（）①正数都有平方根；②负数都有平方根， ③正数都有立方根；④负数都有立方根；A ．1个B ．2个C ．3个D ．4个【例5】 一个自然数的算术平方根为a ，则和这个自然数相邻的下一个自然数是（）．A ．1a +B ．21a +C ．22a + D2.2化简及运算【例6】16的算术平方根是____________．【例7】求下列各式的值：（1234；（56【例8】求下列各式的值（1）2）（3）例题精讲【例9】 81的平方根是____________；2(的平方根是______．【例10】下列各式中x 的值．（1）29x =； （2）22500x -=（3）21(51)303x --=（4）2(100.2)0.64x -=【例11】已知某正数有两个平方根分别是3a +与215a －，求这个正数．【例12】求下列各式的值（12）（3）3（4（56【例13】（1）填表：（2）由上你发现了什么规律？用语言叙述这个规律． （3）根据你发现的规律填空：1.442； 7.696．2.3算术平方根的非负性【例14】x为何值时，下列各式有意义？（1；（234【例15】（2013年怀柔期末）如果0x=，则y x的值是________．【例16】设a a的值是________．例题精讲基础演练【练1】81的算术平方根是____________．【练2】求下列各式的值：（1234【练3】求下列各式的值（1）(（2）-（3）(2-【练4】求下列等式中的x：（1）若2 1.21x=，则x＝______；（2）2169x=，则x＝______；（3）若294x=，则x＝______；（4）若22(2)x=-，则x＝______．【练5】（2012年北京四中期末）若2x-是8的立方根，则x的平方根是___________．【练6】（2013年北大附中）平方根等于本身的数是（）A．0B．1C．-1D．0和1【练7】下列运算中正确的是（）A B3=C1=-D．4=【练8】若x的立方根是4，则x的平方根是______．全能突破【练9】 27－______．【练10】 若59x +的立方根是4，则33x +的平方根是______．【练11】 如4=那么2(66)a -的值是______．【练12】 某数的立方根是它本身，这样的数有（）A ．1个B ．2个C ．3个D ．4个【练13】（2011年北师大月考）下列说法不正确的是（）A ．125的平方根是15±； B 3- C ．()20.1-的平方根是0.1±； D ．81的平方根是9【练14】（2011年北师大月考）81的平方根是_________________；64-的立方根是_________．【练15】 （2012年北京四中期末）若实数,,x y z 满足21202x y z ⎛⎫-+-= ⎪⎝⎭，则x y z ++=_________．【练16】 （2012年交大附中）若实数x ，y 2|313|0x y --=,求2x y +的平方根．能力提升【练17_____。

到！” 猎狗听了很不服气地辩解道：“我已经尽力而为了呀！” 再说兔子带着枪伤成功地逃生回家了，兄弟们都围过来惊讶地问它：“那只猎狗很凶呀，你又带了伤，是怎么甩掉它的呢？” 兔子说：“它是尽力而为，我是竭尽全力呀！它没追上我，最多挨一顿骂，而我若不竭尽全力地跑，可就没命了呀！” 泰勒牧师讲完故事之后，又向全班郑重其事地承诺：谁要是能背出《圣经·马太福音》中第五章到第七章的全部内容，他就邀请谁去西雅图的“太空针”高塔餐厅参加免费聚餐会。 《圣经·马太福音》中第五章到第七章的全部内容有几万字，而且不押韵，要背诵其全文无疑有相当大的难度。尽管参加免费聚餐会是许多学生梦寐以求的事情，但是几乎所有的人都浅尝则止，望而却步了。 几天后，班中一个11岁的男孩，胸有成竹地站在泰勒牧师的面前，从头到尾地按要求背诵下来，竟然一字不漏，没出一点差错，而且到了最后，简直成了声情并茂的朗诵。 泰勒牧师比别人更清楚，就是在成年的信徒中，能背诵这些篇幅的人也是罕见的，何况是一个孩子。泰勒牧师在赞叹男孩那惊人记忆力的同时，不禁好奇地问：“你为什么能背下这么长的文字呢？”
64
10 （3） 3 2
27
（4）3
解： （1） 3 27 3
（2） 3 2 10 3 64 4
27
27 3
（3） 3 27 3 27 3
64
64 4
（4）3 64 64 = - 4 + 4=0
课堂练习：求下列各式的值：
3 0.001 = -0.1 3 216 =6
的事，每当小姨妈讲起那段往事，我就想起那苦难无助地童年，小姨妈无私的爱，让我永远难忘。小姨妈的人生很苦，很少有人去关她，可是她却为我们这些没有母爱的孩子现出了她的青春和所有的爱。
我母亲去世后小姨妈也经常照顾我，关心我。她不但关爱我，还有我的三姨家兄弟妹们。还在我母亲没有去世时，我的三姨妈由于有病去世了，留下四个孩子，最小的才两岁，她为了照顾这四个孩子，就和我三姨父结婚，把他们养大成人，现在孩子们都有了自己的家， 可是小姨妈由于劳累过度，而病倒了，现在病在床上不能自理，当我今年回家看到小姨妈时，我很惭愧，她为我们付出的太多了，可我们又给了她什么，她看到我时那含泪的笑容，我才体会到母爱的无私和伟大，也许她不求我们什么，能常回家看看足矣，可我们却做不到，

第二讲 平方根和立方根重点分析：1.平方根、算术平方根、立方根的概念.（1）平方根：如果x 2=a ，那么x 叫做a 的平方根；（2）算术平方根：正数的正的平方根和0的平方根统称算术平方根，一个数a （a ≥0）的算术平方根记作“a ”；（3）立方根：如果x 3=a ，那么x 叫做a 的立方根，记作“3a ”．2.算术平方根的双重非负性：被开方数是非负数，结果是非负数．3.一个正数有两个平方根且互为相反数，零的平方根是零，负数没有平方根．4.任何数都有立方根，且立方根和被开方数具有同号性．难点分析：1.平方根的概念是通过逆运算来建立的，而且有多种不同情况，这是学生从未遇到过的．2.算术平方根的双重非负性的应用．例1.求下列各数的算术平方根:（1）64; (2)(-3)2; （3）14915; （4）81． 思路点拨：根据算术平方根的定义，求一个数a 的算术平方根可转化为求一个数的平方等于a 的运算，更具体地说，就是找出平方后等于a 的正数．解题过程：（1）∵82=64，∴64的算术平方根是8，即64=8．(2)∵(-3)2=32=9，∴(-3)2的算术平方根是3，即23--）（=3．（3）∵14915=4964，（78）2=4964，∴14915的算术平方根是78，即49151=78． （4）∵81=9，32=9，∴81的算术平方根是3，即81=3.方法归纳：这类问题应按算术平方根的定义去求．易错误区：题(2)要注意(-3)2的算术平方根是3，而不是-3.题（3）当一个数是带分数时，应先化为假分数，然后再求其算术平方根，不要出现类似149161=174的错误.题（4）81=9，所以是求9的算术平方根，而不是求81的算术平方根．例2.求下列各式的值:（1）±81; (2) -16; （3）259; （4）24-）（． 思路点拨： (1)±81表示81的平方根，故其结果是一对相反数；(2)－16表示16的负平方根，故其结果是负数；(3) 259表示259的算术平方根，故其结果是正数；(4)(-4)2表示24-）（的算术平方根，故其结果是正数．解答过程：（1）∵92=81，∴±81=±9．(2)∵42=16，∴－16=-4． （3）∵（53）2=259，∴259=53． （4）∵42=(-4)2，∴24-）（=4．方法归纳：根有关的三种符号±a ，a ，－a 的意义是解决这类问题的关键.±a 表示非负数a 的平方根，a 表示非负数a 的算术平方根，－a 表示非负数a 的负平方根． 易错误区:注意a =±a 在具体解题时，符号“ ”的前面是什么符号，其计算结果也就是什么符号.例3.已知2a-1的平方根为±3，3a+b-1的算术平方根为4，求a+2b 的平方根．思路点拨：先根据2a-1的平方根为±3，3a+b-1的算术平方根为4求出a ，b 的值，继而求出a+2b 的值，再由平方根的定义进行解答即可．解题过程：∵2a-1的平方根为±3，∴2a-1=9,解得a=5．∵3a+b-1的算术平方根为4，∴3a+b-1=16，即15+b-1=16,解得b=2．∴a+2b=5+4=9．∴a+2b 的平方根为±3．方法归纳：本题考查的是平方根及算术平方根的定义，熟知一个数的平方根有两个，这两个数互为相反数等知识点是解答本题的关键．易错误区：题目求的是a+2b 的平方根，而不是求a+2b 的值.一个数的平方根有两个，注意不要漏解．例4.已知：y=2-a +）（1b 3+，当a ，b 取不同的值时，y 也有不同的值.当y 取最小值时，求b a 的非算术平方根（即负平方根）．思路点拨：y=2-a +）（1b 3+，要y 最小，就是要2-a 和）（1b 3+均取最小值，而2-a ≥0，）（1b 3+≥0，显然是当2-a =0和）（1b 3+=0时y 取最小值，即a=2，b=－1．解答过程：∵y=2-a +）（1b 3+，2-a ≥0，）（1b 3+≥0, ∴当2-a =0和）（1b 3+=0时，y 最小. 由2-a =0和）（1b 3+=0，可得a=2，b=－1． ∴b a 的非算术平方根是-1=-1．方法归纳：本题主要考查了算术平方根的非负性、一个数的算术平方根的最小值为0两个知识点．易错误区：本题是用的算术平方根结果的非负性，而不是用的被开方数的非负性．例5.先阅读所给材料，再解答下列问题：若1-x 与x -1同时成立，则x 的值应是多少？有下面的解题过程：1-x 和x -1都是算术平方根，故两者的被开方数x-1，1-x 都是非负数，而x-1和1-x 互为相反数.两个非负数互为相反数，只在一种情形时成立，那就是它们都等于0时，即x-1=0，1-x=0时，故x=1．问题：已知y=2x -1+1-2x +2，求x y 的值．思路点拨：根据阅读材料中的信息，当两个被开方数互为相反数时，这两个被开方数只能同时等于0，可通过先求得x 的值，再进一步得出y 的值的方式解答．解题过程：由阅读材料提供的信息，可得1-2x=0且2x-1=0，∴x=21.进而可得y=2．∴x y =（21）2=41． 方法归纳：首先要认真阅读题目所给的材料，总结出正确的结论，然后用所得的结论解决问题.本题由材料得出的结论是：互为相反数的两个数都在根号内，那么这两个数都为0． 易错误区：算术平方根的双重非负性具有两层含义：一是被开方数是非负数，二是它的运算结果是非负数.本题主要运用了被开方数是非负数这一性质．请你认真观察下面各个式子，然后根据你发现的规律写出第④，⑤个式子．思路点拨：要写出第④、⑤个式子，就要知道它们的被开方数分别是什么，为此应认真观察所给式子的特点.通过观察，发现前面三个式子的被开方数分别是用序数乘以16得到的，故第④、⑤个式子的被开方数应该分别是64和80．解题过程：方法归纳：解这类题需注意分析题目所给的每个式子的特点，然后从特殊的例子出发，推广到一般的结论．易错误区：按规律找出被开方数后，要利用算术平方根的性质对其进行化简．拓展训练A 组1.4的平方根是±2，那么81的平方根是( )．A.±9B.9 ]C.3D.±32.下列各组数中互为相反数的是( )．A.－2与22-）（B.－2与8-3C.－2与-21 D.｜－2｜与2 3.使等式(-2x -)2=x 成立的x 的值( )．A.是正数B.是负数C.是0D.不能确定4.若2m －4与3m －1是同一个数的平方根，则m 为( )．A.－3B.1C.－3或1D.－15. a -3在实数范围内有意义，则a 的取值范围是( )．A.a ≥3B.a ≤3C.a ≥―3D.a ≤―36.数n 的平方根是x ，则n+1的算术平方根是( )．A. 1x +B. 1x 2+C.x+1D.不能确定7.如果y=8-x +x -8+2，那么xy 的算术平方根是( )． A. 2 B. 8 C.4 D. 68.（1）写一个比-3小的整数 ；(2)已知a ，b 为两个连续的整数，且a<28<b ，则a+b= ．9.一个正方体的体积为285cm 3，则这个正方体的一个侧面的面积为 cm 2（结果保留3位有效数字）．10.若a 的一个平方根是b ，则它的另一个平方根是 ；若a 的一个平方根是b ，则a 的平方根是 ． 11. 64的平方根是 ，算术平方根是 ，立方根是 ．12.求下列各式的值：（1）44.1； (2)- 3027.0；（3）649； （4）44.1-21.1． B 组13.如果一个正数的平方根是a+3与2a-15，那么这个正数是( )．A.7B.8C.49D.5614.估计6+1的值在( )．A.2和3之间B.3和4之间C.4和5之间D.5和6之间15.在实数0，-π，1.58×10-7，-4中，最小的数是( )．A.0B.-πC.1.58×10-7D.-416.下列说法：①只有正数才有平方根；②-3是9的平方根；③7的平方根是-7；④±11都是11的平方根；⑤（-3）2的平方根是-3.其中正确的有( )．A.①②③B.③④⑤C.③④D.②④17.已知5=a ，14=b ，则063.0=( ).A. 10ab B. 103ab C. 100ab D. 1003ab 18.（1）用计算器估算：若2.6456＜a ＜2.6459，则a 的整数值是 ；(2)用计算器比较大小：317．（填“＞”、“=”或“＜”）19.已知一个正数的平方根是2a －1与2－a ，求a 的平方的相反数的立方根．20.天气晴朗时，一个人能看到大海的最远距离s （单位：km ）可用公式s 2=16.88h 来估计，其中h （单位：m ）是眼睛离海平面的高度.如果一个人站在岸边观察，当眼睛离海平面的高度是1.5m 时，能看到多远（精确到0.01km ）？如果登上一个观望台，当眼睛离海平面的高度是35m 时，能看到多远（精确到0.01km ）？走进重高1.【莱芜】4的算术平方根为（ ）.A.-2B.2C.±2D. 22.【毕节】38的算术平方根是（ ）.A.2B.±2C. 2D.±23.【宁波】已知实数x ，y 满足2-x +（y+1）2=0，则x －y 等于( )．A.3B.－3C.1D.－14.【天津】已知一个表面积为12dm 2的正方体，则这个正方体的棱长为（ ）.A.1dmB. 2dmC. 6dmD. 12dm5.【德阳】若实数x ，y 满足（2x+3）2+|9-4y|=0，则xy 的立方根为 .6.【呼和浩特】实数a ，b 在数轴上的位置如图，则2b a ）（ +a 的化简结果为 ．(第6题)高分夺冠1.在如图所示的数轴上，点B 与点C 关于点A 对称，A ，B 两点对应的实数分别是3和-1，则点C 所对应的实数是( )．(第1题) A.1+3 B.2+3 C.23-1 D.23+12.如果200a 是一个整数，那么满足条件的最小正整数a= ；若3x 128是一个正整数，则满足条件的最小正整数x= ．3.①ab=0；②a+b=0；③a 2+b=0；④a -b =0；⑤a+2b 2=0.以上5个等式中使得实数a ，b 的值一定同时为0的编号是 ．4.请同学们运用所学的方法，完成下表：（1）观察下表并说明当数a 的小数点向右（或向左）移动时，它的立方根3a 的小数点的移动规律是怎样的？写出你发现的规律；(2)运用你所发现的规律，解下列各小题： 已知35.250=1.738，求：①350.00525；②35250000．5.如图，已知每个小正方形的边长均为1，则图中阴影正方形的面积是多少？它的边长是多少？(第5题)。

教 学 过 程
一、创设情境
做一做
计算下列各题，看谁做得又快又准？
(1)(a+b)(a-b) (3)(2a+b)(2a-b)ቤተ መጻሕፍቲ ባይዱ
(2)(x+y)(x-y) (4)(2m+3)(2m-3)
教 学 过 程
二、探求新知 自主学习 解决问题
1、让学生分析老师或某些同学做得快的原因
1) 先独立思考
2) 交流讨论 3) 全班展示交流结果 2、小组讨论，分析公式特征结构
第14章 整式的乘法
14.3 乘法公式
教 材 分 析
1、从教材的性质地位与作用看
2、从学生学习过程的角度看
3、重点、难点和关键
重点: 平方差公式的理解 难点: 平方差公式的应用 关键: “认清结构，找准a、b”.
目 标 分 析
知识与能力：
熟记平方差公式，能说出平方差公式的结构特征，会用 平方差公式进行运算. zxxk
教 学 过 程
六、反思小结 1、本节你学到了什么？
2、本节课你有何收获？
3、通过本节课学习，你有何感受? 4、你还有什么疑惑?
作业
拓展训练
(1) 计算 3982-3992
(2) 在式子(-3a+ )( )的括号内填入怎样的式子 才能用平方差公式计算. Z,xxk
谢谢
(2) (2x+y)(y-2x)
3、观察：(-2x+y)( ),在括号内填入怎样的代数式， 才能运用平方差公式进行计算？
教 学 过 程
四、反馈练习 巩固新知
判断正误，如果错误，应怎样改正？ ( 1 ) (-a-b)(a-b)=-a2+b2 ( 2 ) (-a+b)(-a-b)=-a2-b2 ( ) ( )

（3） 25 36
5 （6） - 3 125 5
6
82
PPT课件
11
不 要 遗 漏 哦！
解下列方程：
1. 9(3 y)2 4
解: (3 y)2 4 9
2 3 y
3
y 3 23Βιβλιοθήκη y 2 1 或y 3 2
3
3
2. 2（7 x 5）3 8 0
解:
3
27(x

5)3

8
3
(x 5)3 8
3
27
x5 2 33
x52 33
x 1
当方程中出现平方时，若有解，一般都有 两个解
当方程中出现立方时，一般都有一个解
PPT课件
12
解方程：
（1）（x-1）3 125 （4）2（7 x 2）3 125 0
（2）23x 12 8
x2=a那么这个数X叫做a的平方根（也叫
做二次方根）。记为“ a ”读作“正、
负 根号a”
PPT课件
2
立方根的定义.
一般地，如果一个数的立方等于a，这个 数就叫做a的立方根(也叫做三次方根).
用式子表示，如果X3 =a，那么X叫做a的立方根.
数a的立方根用符号“3 a ”表示,读作“三次根号a
其中a是被开方数,3是根指数(注意:根指数3不能省 略).
PPT课件
3
区别
你知道算术平方根、平方根、立方根联 系和区别吗？
算术平方根
平方根
立方根
表示方法
a 的取值
正数
性
0
质
负数
开 方 是本身
a ≠ a

平方根与立方根课件一、引言平方根与立方根是数学中常见的概念，在实际生活中也有着广泛的应用。

本课件将详细介绍平方根与立方根的概念、计算方法以及应用场景，帮助学生深入理解并掌握相关知识。

二、平方根的概念与计算1. 平方根的定义：平方根是指一个数的平方等于被开方数的数，也就是对于非负实数a，满足a^2=b，那么b就是a的平方根。

2. 平方根的计算方法：通过数学运算，我们可以得到平方根的计算方法，其中包括牛顿迭代法、二分法等。

课件将逐一介绍这些方法，并通过示例演示具体的计算步骤。

三、立方根的概念与计算1. 立方根的定义：立方根是指一个数的立方等于被开方数的数，也就是对于实数a，满足a^3=b，那么b就是a的立方根。

2. 立方根的计算方法：与平方根类似，立方根也有多种计算方法，如二分法、牛顿迭代法等。

课件将详细解释这些方法，并提供示例，帮助学生掌握立方根的计算步骤。

四、平方根与立方根的应用场景1. 面积和体积计算：平方根和立方根在几何计算中有着广泛的应用，可以用于计算图形的面积和体积。

2. 物理学中的应用：平方根和立方根在物理学中也有着重要的应用，例如在速度、加速度以及力的计算中。

3. 统计学中的应用：平方根和立方根在统计学中常用于计算方差和标准差等指标。

五、小结平方根与立方根是数学中的重要概念，通过本课件的学习，我们深入了解了它们的定义、计算方法以及应用场景。

希望本课件能够帮助学生更好地掌握平方根与立方根的知识，提升数学能力。

六、参考文献[参考文献1][参考文献2][参考文献3]。