第十届小学希望杯全国数学邀请赛五年级一试试卷及答案
- 格式:doc
- 大小:924.50 KB
- 文档页数:5

(完整)最新五年级希望杯近⼏年试题2010年第⼋届⼩学“希望杯”全国数学邀请赛五年级第1试试题1、计算 10.37×3.4+1.7×19.26=。
2、已知1.08÷1.2÷2.3=10.8÷□,其中□表⽰的数是。
3、计算:1.825gg-0.8g=。
(8、5、8的上⾯有循环点)4、有三个⾃然数a ,b ,c ,已知b 除以a ,得商3余3;c 除以a ,得商9余11。
则c b ,得到的余数是。
5、已知300=2×2×3×5×5,则300⼀共有不同的约数。
6、在99个连续的⾃然数中,最⼤的数是最⼩的数的25.5倍,那么这99个⾃然数的平均数是。
7、要往码头运28个同样⼤⼩的集装箱,每个集装箱的质量是1560千克。
现安排⼀辆载重6吨的卡车运送这些集装箱,卡车车厢的⼤⼩最多可以容纳5个集装箱,则这辆卡车⾄少需往返趟。
8、⼩晴做道菜:“⾹葱炒蛋”,需7道⼯序,时间如下:洗葱,切葱花打蛋搅拌蛋液和葱花洗锅烧热锅烧热油烧菜1分钟半分钟 1分钟半分钟半分钟半分钟 2分钟做好这道菜⾄少要分钟。
9、⼀项特殊的⼯作必须⽇夜有⼈看守,如果安排8⼈轮流值班,当值⼈员为3⼈,那么,平均每⼈每天⼯作⼩时。
10、甲、⼄两商店中某商品的定价相同。
甲商店按定价销售这种商品,销售额是7200元;⼄商店按定价的⼋折销售,⽐甲商店多售出15件,销售额与甲商店相同。
则甲商店售出件这种商品。
11、夜⾥下了⼀场⼤雪,早上,⼩龙和爸爸⼀起步测花园⾥⼀条环形⼩路的长度,他们从同⼀点同向⾏⾛。
⼩龙每步长54厘⽶,爸爸每步长72厘⽶,两⼈各⾛完⼀圈后⼜都回到出发点,这时雪地上只留下60个脚印。
那么这条⼩路长⽶。
12、⼀艘客轮在静⽔中的航⾏速度是26千⽶/时,往返于A 、B 两港之间,河⽔的流速是6千⽶/时。
如果客轮在河中往返4趟公⽤13⼩时,那么A 、B 两港之间相距千⽶。

五年级数学希望杯试题第五届“希望杯”全国数学邀请赛(五年级第1试)1.2007÷=______。
2.对不为零的⾃然数a,b,c ,规定新运算“☆”:☆(a,b ,c)= ,则☆(1,2,3)=______。
3.判断:“⼩明同学把⼀张电影票夹在数学书的51页⾄52页之间”这句话是______的。
(填“正确”或“错误”)4.已知a,b,c是三个连续⾃然数,其中a是偶数。
则a+1,b+2,c+3的积是奇数还是偶数5.某个⾃然数除以2余1,除以3余2,除以4余1,除以5也余1,则这个数最⼩是______。
6.当p和p3+5都是质数时,+5=______.7.下列四个图形是由四个简单图形A、B、C、D(线段和正⽅形)组合(记为*)⽽成。
则图中①~④中表⽰A*D的是______。
(填序号)8.下⾯四幅图形中不是轴对称图形的是______。
(填序号)9.⼩华⽤相同的若⼲个⼩正⽅形摆成⼀个⽴体(如图)。
从上⾯看这个⽴体,看到的图形是图①~③中的______。
(填序号)10.图中内部有阴影的正⽅形共有______个。
11.下图中的阴影部分BCGF是正⽅形,线段FH长18厘⽶,线段AC长24厘⽶,则长⽅形ADHE的周长是______厘⽶。
12.图中的熊猫图案的阴影部分的⾯积是______平⽅厘⽶。
(注:阴影部分均由半圆和正⽅形组成,图中⼀个⼩正⽅形的⾯积是1平⽅厘⽶,π取3.14) 13.⼩红看⼀本故事书,第⼀天看了这本书的⼀半⼜10页,第⼆天看了余下的⼀半⼜10页,第三天看了10页正好看完。
这本故事书共有______页。
14.有⼀副扑克牌中(去掉⼤、⼩王),最少取______张牌就可以保证其中3张牌的点数相同。
15.如图,摩托车⾥程表显⽰的数字表⽰摩托车已经⾏驶了24944千⽶,经过两⼩时后,⾥程表上显⽰的数字从左到右与从右到左的读数相同,若摩托车的时速不超过90千⽶,则摩托车在这两⼩时内的平均速度是______千⽶/时。

历届五年级希望杯答案及解析2010年第八届2011年第九届1、解:原式=1.25 ×31.3 ×3 ×8 = 100 ×93.9 = 9392、解:将循环节多写一次即可逐位比较3、解:十位数之前应该有1 + 2 + 3 +……+9 = 45位。
1位数有9位,10—19有20位,20—27有16位,所以十位数的开头应为28,为28293031324、解:从A到B一定会经过三步,第一步要从A走到中间,最后一步应该是从中间走到B,而第二步为从中间走到中间只能有一种走法。
从A到中间一条线上共有5种走法,从B到中间一条线上也有5种走法。
所以共有5 ×1 ×5 = 25种走法。
5、解:在3 ×4的长方形中有20个横平竖直的正方形。
斜着的有1 ×1正方形17个,2 ×2的正方形8个,还有1个3 ×3的大正方形。
共46个。
6、解:47 ÷b = c ……c ,即b ×c + c = 47,即c ×( b + 1 ) = 47,所以c一定是47的约数,c为47肯定不符合条件,所以c = 1,即除数是46,余数是1.7、解:能被90整除说明即能被9整除也能被10整除,被10整除说明最后一位是0,被9整除说明数字和应为9的倍数,即2 + 0 + 1 + 1 + a +0 是9的倍数,所以a = 5,即后两位是50.8、解:约数个数为奇数说明这个自然数为完全平方数,1000以内最大的完全平方数是31²= 9619、解:首先最下面的一个角肯定没有,最上面的中部也会少一部分,所以是丁。
10、解:一圈共400米,甲是乙速度的1.5倍,所以甲共走了240米,乙走了160米。
DE为60米,CE为40米。
SADE = 3000平方米,SBCE = 2000平方米,差为1000平方米。
11、解:弟弟如果不多跑半小时应比哥哥少跑80 ×30 — 900 = 1500米,所以哥哥共跑了1500 ÷(110—80)= 50分钟,共跑了50 ×110 = 5500米。

2021希望杯五年级1-2试参考答案1第十二届小学“希望杯”全国数学邀请赛五年级第1试试题1.202103165?,余数是 .【考点】数论,整除特征【答案】1【分析】5的整除特征是看个位除以5的余数即可.6除以5余1,故原数除以5也余1.2. 用1、5、7组成各位数字不同的三位数,其中最小的质数是 2.【考点】数论,质数判别,最值【答案】157【分析】首先考虑百位为1;多位数质数的个位不可能为5,故若1在百位,则5只能在十位,进而7在个位.检验157是否为质数:157不是2、3、5、7、11的倍数,故157是质数.3. 10个2021相乘,积的末位数是 3.【考点】数论,余数性质【答案】6【分析】末尾即为此数除以10的余数.根据余数的可乘方性,101025520214(4)66(mod10)oooo, 4.有一列数:1、2、2、3、3、3、4、4、4、4、??每个数n都写了n次.当写到20的时候,数字1出现了. 【考点】计算,数列,页码问题变型【答案】157 【分析】出现过1的数有:1(1个)、10(10个)、11(21122′=个)、12(12个)、13(13个)、??、 19(19个),共有1101121213 一个小数,若去掉小数点,则得到的整数与原小数的和是201.3,那么这个小数是 .【考点】数论,位值原理【答案】18.3【分析】和是201.3,说明原小数的小数部分必定为0.3.故当去掉小数点时,此数扩大到了原来的10倍;再加上自身,得到的和应为原来的11倍,故此数原来是201.31118.3?=.6. 已知三位数abc与cba的差198abccba-=,则abc最大是 .【考点】数论,位值原理,最值【答案】997【分析】用位值原理将条件式按数位拆开:(10010)(10010)9999198abccbaac++-++=-=,故 2ac-=.要abc最大,则要a最大,令9a=,则7c=.b没有限制,故令9b=.abc最大是997. 7.若将20表示成若干个互不相同的奇数的和,那么,不同的表示方法有种.(加数相同,相加的次序不同,算作同一种表示方法.如119+与191+算作同一种表示方法.)【考点】计数,整数分拆,奇偶性【答案】7【分析】20是偶数,故只能分拆成偶数个奇数的和,但6个不同的奇数相加至少是135791136+++++=,故知20最多只能分拆成4个不同的奇数相加.字典排列法:20219317515713911=+=+=+=+=+135111379=+++=+++.共7种. 8.A、B两家面包店销售同样的面包,售价相同.某天,A面包店的面包售价打八折,A面包店这天的营业额是B面包店营业额的1.2倍,则A面包店售出的面包数量是B面包店的倍. 【考点】应用题,经济问题【答案】1.5 【分析】售价×数量=营业额 B:111′=;A:0.8?1.2′=.故知答案是1.20.81.5?=倍. 9.甲桶内有水4升,乙桶内有水13升,向两个桶内加入同样多的水后,乙桶内的水是甲桶内的水的3倍(水不溢出),那么,向每个桶内加入的水是升.【考点】应用题,列方程解应用题【答案】0.5(或可写作 1 2 )【分析】设每个桶内加入的水是x升,则有方程133(4)xx+=+,解得0.5x=. 10.一只蚂蚁从墙根竖直向上爬到墙头用了4分钟,从墙头沿原路返回到出发点用了3分钟.若蚂蚁第二分钟比第一分钟多爬1分米,第三分钟比第二分钟多爬1分米,??,整个过程中,每分钟爬过的路程都比前一分钟多爬1分米,则墙高米.【考点】应用题,列方程解应用题,等差数列【答案】4.2【分析】设第一分钟爬了x分米,则有方程(1)(2)(3)(4)(5)(6)xxxxxxx++++++=+++++,即46315xx+=+,解得9x=,故墙高910111242+++=分米,即4.2米.11.如图,五边形ABCDE内有一点O,O点到五条边的垂线段的长都是4厘米,五边形的周长是30厘米,则五边形ABCDE的面积是平方厘米. 444 44E D C B AO【考点】几何,图形分割,三角形面积公式 3【答案】60【分析】连接OA、OB、OC、OD、OE,则ABCDEOABOBCOCDODEOEASSSSSS=++++△△△△△4242424242ABBCCDDEEA=′?+′?+′?+′?+′?()42 ABBCCDDEEA=++++′?3042=′?60=(平方厘米)12.一天,小华去一栋居民楼做社会调查,这栋楼有15层,每层有35个窗户,每两户人家有5个窗户.若每户人家需要一份调查表,则小华至少应带调查表份. 【考点】应用题【答案】210【分析】每层有355214?′=户人家,故共有1415210′=户人家.13.如图,一个四边形花园的四条边长分别是63米、70米、84米、98米,规定:在花园的四角和边上种树,相邻两棵树的间距是相等的整数(单位:米),则至少植树棵. 84米 70米 63米 98米【考点】数论,最大公因数,间隔问题【答案】45【分析】由于是首尾相连的图形,故树的棵数与间隔数相等,而(63,70,84,98)7=,故相邻两棵树的最大间距是7.总间隔数最少是(63708498)7910121445+++?=+++=个,即至少植树45棵.14.小红和小亮玩“石头剪刀布”的游戏,约定:在每个回合中,如果赢了就得3分,输了就扣2分,每个回合都分出胜负.游戏开始前,两人各有20分,玩了10个回合后,小红的得分是40分,则小红赢了个回合.【考点】应用题,鸡兔同笼型问题【答案】8【分析】方法一(算术):如果小红全输,最终应得202100-′=分,与实际得分相差40分;一个回合之内,赢比输多得325+=分,故知小红赢了4058?=个回合. 方法二(代数):设小红赢了x个回合,则小红输了(10)x-个回合,故有方程 2032(10)40xx+--=,解得8x=.15.如图,线段AB和CD垂直且相等,点E、F、G是线段AB的四等分点,点E、H是线段CD的三等分点,从A、B、C、D、E、F、G、H这8个点中任选3个作为顶点构成三角形,其中,面积与△CFE面积相等的三角形(不包括△CFE)有个.4HGFE D CBA【考点】组合,几何,计数【答案】10【分析】设3AEEFFGGB====,则4CHHEED===.则283CEFSCEEF=′=′△,同样为83 ′型的三角形还有△CEA、△HDF、△HDA;但246CEFS=′△,46′型的三角形有△CHG、△HAF、△HEG、△HFB、△DAF、△DEG、△DFB.共有10个. 16.一个长方体的长、宽、高都是两位数(其中长的值最大),并且它们的和是偶数.若这个长方体的体积是2772、2380、3261、4125这四个数中的一个,则这个长方体的长是. 【考点】数论,奇偶性,分解质因数【答案】21【分析】长、宽、高不可能都是奇数,否则和不可能是偶数.所以这三个数中必有偶数,乘积必为偶数,故体积只可能是2772和2380这两个数中的一个.但2238025717=′′′,故知2380分拆成三个两位数相乘只有一种拆法:2380101417=′′,但此时长、宽、高的和不是偶数,所以体积是2772.22277223711=′′′,分拆成三个两位数相乘有两种拆法:111418′′(舍,和不是偶数)或111221′′,故知长为21.17.如图,用35个棱长为1的小正方体堆成一个大的几何体,这个几何体的表面积(含底面积)是 .【考点】立体几何,三视图法求表面积【答案】90 【分析】三视图法:()2=+++′堆叠体表面积正视图面积俯视图面积侧视图面积凹槽数(1415160)2=+++′90=18.若115、200、268被某个大于1的自然数除,得到的余数都相同,那么,用2021除以这个自然数,得到的余数是 .【考点】数论,同余定理【答案】8【分析】设这个自然数为x,则(200115)x-,且(268200)x-,即85x且68x,故知x是85和68的公因数.(85,68)17=,故17x.又x是大于1的自然数,故 519.一辆汽车从甲地开往乙地,若每小时行45千米,则将比原计划迟到1小时;若每小时行60千米,则将比原计划早到1小时.那么,甲、乙两地的距离是千米.【考点】行程问题,列方程解行程【答案】360 【分析】设原计划用时为x小时,以两地全长为等量关系列方程:45(1)60(1)xx+=-,解得7x=.故两地全长为45(71)360′+=千米. 20.若算式11个的得数是整数,则m的值最大是. 【考点】数论,质因数分解【答案】102【分析】2021!中11的数量:[202111]183?=,[18311]16?=,[1611]1?=,共183161200++=个; 999!中11的数量:[99911]90?=,[9011]8?=,共90898+=个;则中11的数量为20218102-=个2021年第十二届小学“希望杯”全国数学邀请赛五年级第2 试详细解答一、填空题(每题5 分,共60 分。


第一届小学“希望杯”全国数学邀请赛试题答案(五年级第一
试)
无
【期刊名称】《数学小灵通:小学中高年级班》
【年(卷),期】2004(000)003
【总页数】1页(P8)
【作者】无
【作者单位】无
【正文语种】中文
【中图分类】G623.5
【相关文献】
1.第二届小学“希望杯”全国数学邀请赛五年级第1试试题 [J], 苏晓玲
2.第一届小学“希望杯”全国数学邀请赛试题答案(四年级第1试) [J], 无
3.第四届小学“希望杯”全国数学邀请赛五年级第1试试题 [J], 苏晓玲
4.第二届小学“希望杯”全国数学邀请赛五年级第2试试题 [J], 苏晓玲
5.第四届小学“希望杯”全国数学邀请赛五年级第2试试题 [J], 苏晓玲
因版权原因,仅展示原文概要,查看原文内容请购买。

“希望杯”全国数学邀请赛模拟练习专题专题1 四则运算1.2.7+7.2+2.8+8.22.2280÷34-648÷34+476÷343.1÷﹙2÷3﹚÷﹙3÷4﹚÷﹙5÷6﹚4.0.2008+2.008+20.08+200.8+20085.7.5×23+3.1×256.19+199+1999+199997.﹙12.34+23.41+34.12+41.23﹚÷﹙1+2+3+4﹚8.﹙1+3+5+...+99﹚-﹙2+4+6+ (98)9.41.2×8.1+537×0.1910.1÷0.1÷0.1÷0.1÷0.111.﹙8.5×13.3×7.2﹚÷﹙1.7×1.8×1.9﹚12.99+99×99+99×99×9913.2009.2009+99.99×20.0914.1÷0.0625-1÷0.125-1÷0.25-1÷0.515.如果12345679×a=66666666, 12345679×b=555555555,那么a+b=____.专题2 自然数的性质1.用0,1,2,3这四个数字可以组成___个无重复的四位数。
2.有七张卡片:1,1,2,3,9,9,9,从中任取3张可排列成三位数。
若其中卡片9旋转后可看做6,则排列成偶数有___个。
3.有两组数,A组:1,3,5,7,9,B组:2,4,6,8,10.分别从A组和B组中任意选出一个数相加,能得到___个不同的和。
4.能同时被2,3,4,5,6,7,8,9整除的最小五位数是____。
5.p,q均为质数,且5p+7q=29,则p+q=___。
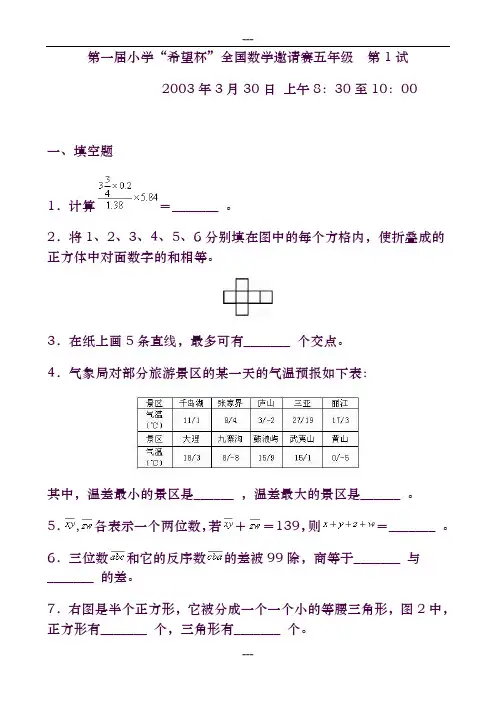
第一届小学“希望杯”全国数学邀请赛五年级第1试2003年3月30日上午8:30至10:00 一、填空题1.计算=_______ 。
2.将1、2、3、4、5、6分别填在图中的每个方格内,使折叠成的正方体中对面数字的和相等。
3.在纸上画5条直线,最多可有_______ 个交点。
4.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是______ ,温差最大的景区是______ 。
5.,各表示一个两位数,若+=139,则=_______ 。
6.三位数和它的反序数的差被99除,商等于_______ 与_______ 的差。
7.右图是半个正方形,它被分成一个一个小的等腰三角形,图2中,正方形有_______ 个,三角形有_______ 个。
8.一次智力测验,主持人亮出四块三角形的牌子:在第(4)块牌子中,?表示的数是_______ 。
9.正方形的一条对角线长13厘米,这个正方形的面积是平方厘米。
10.六位自然数1082□□能被12整除,末两位数有种情况。
11.右边的除法算式中,商数是。
12.比大,比小的分数有无穷多个,请写出三个:。
13.A、B、C、D、E五位同学进行乒乓球循环赛(即每2人赛一场),比赛进行了一段时间后,A赛了4场,B赛了3场,C赛了2场,D 赛了1场,这时,E赛了场。
14.观察5*2=5+55=60,7*4=7+77+777+7777=8638,推知9*5的值是。
15.警察查找一辆肇事汽车的车牌号(四位数),一位目击者对数字很敏感,他提供情况说:“第一位数字最小,最后两位数是最大的两位偶数,前两位数字的乘积的4倍刚好比后两位数少2”。
警察由此判断该车牌号可能是。
16.一个小方木块的六个面上分别写有数字2,3,5,6,7,9。
小光,小亮二人随意往桌上扔放这个木块。
规定:当小光扔时,如果朝上的一面写的是偶数,得1分。
当小亮扔时,如果朝上的一面写的是奇数,得1分。
每人扔100次,得分高的可能性最大。

第十五届(2017年)小学“希望杯”全国数学邀请赛五年级培训题1. 计算:2016×20172017-2017×20162016.2. 计算:32.2÷2.7+386÷54-4.88÷0.27.3. 计算:6051×0.125-0.375×1949+3.75×1.2.5. 用[a]表示不超过 a的最大整数,{a}表示 a 的小数部分,即{a}=a-[a],定义一种运算“⊕”:a⊕b=(a-b)÷(b+1),求[3.9]⊕{5.6}+[4.7]的值.6. 找规律,填数:0,2,12,36,80,150,252,______,_______,…7. 如图 1 所示的七个圆填入七个连续自然数,使每相邻圆的数之和等于连线上的数,求这七个自然数的和.8. 有一串数,最前面的 4 个数是 2,0,1,6,从第 5 个数起,每一个数是它前面相邻 4 个数之和的个位数字,问在这一串数中,会依次出现 2,0,1,7 这 4个数吗?9. 小华在电脑上玩一种游戏:输入一个大于零的自然数,则输出的数比输入的数扩大一倍还多 1,若先输入的数既不是质数,也不是合数,再将输出的数输入,…则输出的数中,首先超过100的数是多少?10. 从1123个1×1的正方形纸片中,依次取出 1个,3个,5个,7 个,…,(2n-1)个,求最大的n.11. 已知x是两位数,y是一位数,若1123=x× x+11y× y,求x+y.12. 20152015+20162016+20172017的个位数字是多少?(定义:x n表示n个 x相乘)13. 1×2×3×4×…×2016×2017 的积的末尾有多少个连续的 0?14. 111a是四位数,若111a-3是7的倍数,求自然数a.15. 有三个连续的自然数,它们的和是三位数,并且是 31 的倍数,求这三个数的和的最小值.16. 若是四位数,并且-3是7的倍数,那么a + b有多少个不同的值?17. 100 名同学面向老师站成一行.大家先从左至右按 1,2,3,…依次报数;再让报数是 4 的倍数的同学向后转,接着又让报数是 5 的倍数的同学向后转. 问:背向老师的有多少人?18. 一个自然数,它除了 1以外的两个不同约数的和最大是 60,求这个自然数.19. 三位数中,被6 除,余数是5的有多少个?20. 有一类四位数,除以5余3,除以7余6,除以9余6,求这类四位数中最小的数.21. 求被 7除余5,被8除余2的最小的三位数.22. 是三位数,若-a可被13整除,求自然数a的最小值.23 .是三位数,若+1 是7的倍数,-1是13的倍数,求自然数 a.24. ,求a÷7 得到的余数.25. 五年级(2)班同学分为 5 组,按组活动.第一组到第五组的人数分别是 12 人,6人,10人,13人,7 人. 其中有一个小组需要留在教室,其余四组去操场跑步和跳绳,若跑步的人数比跳绳的人数的 2 倍多5人,则留在教室的是第几组?26. 小华将连续偶数 2,4,6,8,10,…逐个相加,结果是2016. 验算时发现漏加了一个数,那么,这个漏加的数是多少?27. 三个质数的平方和是 390,这三个质数分别是多少?28. 3个不同的质数 a,b,c满足a+b=c,且 b× c=143,求a×(b+c)的值.29. 下面是著名的百羊问题.原文如下:《算法统宗》(明)程大位甲赶羊群逐草茂,乙拽一羊随其后,戏问甲及一百否? 甲云所说无差谬,所得这般一群凑,再添半群小半群,得你一只来方凑,玄机奥妙谁猜透?原文的意思是说,一个牧羊人赶着一群羊,有人牵着一只羊从后面跟来,问牧羊人:“你这群羊有 100 只吗?”牧羊人说:“如果我再有这样一群羊,加上这群羊的一半,再加上一半的一半,连同你这一只羊,就刚好满 100 只.”请问牧羊人赶着多少只羊?30. 用两个 3,三个 2,两个1可以组成多少个互不相同的七位数?31. 从1 到2017的所有奇数的平方数中,个位数是 5的有几个?32. 从1 到101这101 个自然数中,(1) 至少选出_____个才能保证其中一定有两个数的和是 7的倍数;(2) 如果要保证其中一定有两个数的和是 6的倍数至少要选出______个.33. A,B,C,D四人久别重逢.(1) 四人站成一排照相,问有多少种站法?(2) 四人围成一圈照相有多少种站法?34. 电视台打算 3天播完 6集电视剧,其中可以有若干天不播,共有多少种播出的方法?35. 属相各异的 12 位同学按鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、犬、猪的顺序围成一圈传递一袋不足 200 颗糖的幸运礼包.每人接到礼包后取出一颗糖,然后将礼包往下传.属牛的最牛,先取糖,将礼包传给属虎的同学,…,若最后取到糖的同学属龙,则(1) 礼包里至少有多少颗糖?(2) 礼包里至多有多少颗糖?36. 纸箱中有赤,橙,黄,绿,青,蓝,紫七色袜子,每种袜子都是单色,且数量足够多,那么从中至少取多少只袜子可以保证有一双同色的袜子?37. 五年(1)班有 46 名学生参加 3 项活动.其中有 24 人参加了数学小组,20 人参加了语文小组,参加美术小组的人数是既参加数学小组又参加美术小组人数的 4倍,又是3项都参加的人数的 8倍,既参加美术小组也参加语文小组的人数是 3项都参加的人数的 3 倍,既参加数学小组又参加语文小组的有 10 人,问参加美术小组的人数是多少?38. 有1 克、2克、4 克、8克、16 克重的砝码 5枚,若只能在一边放砝码,问:(1) 用这些砝码可称出多少种不同的重量?(2) 若4克的砝码破损后只剩下 3克,则可称出多少种不同的重量?39. 小明家住在一条胡同里,这条胡同里的门牌从 1号、2号、…连续下去.全胡同所有住户的门牌号之和减去小明家的门牌,其结果为265. 则(1) 这条胡同共有多少家住户?(2) 小明家的门牌是几号?40. 数一数,图2中共有多少个三角形?41. (1) 图3中有多少个长方形(包括正方形)?(2) 图3中包含*的长方形有多少个(包括正方形)?42. 波兰数学家尔宾斯基(Sierpinski)在1915年提出了尔宾斯基三角形. 以下是它的构造方法:①取一个实心的等边三角形;②沿三边中点的连线,将它分成四个小三角形;③去掉中间的那一个小三角形;④对其余三个小三角形重复②③④.这样下去可以重复无数次操作,如图 4 所示. 如果原来的大等边三角形面积为256,那么在 4次操作之后,三角形中被去掉的空白部分面积为多少?43. 如图 5,8个小等边三角形组成了一个梯形.(1) 数一数图5中有几个等边三角形;(2) 若去掉一个三角形,使得三角形的总数减少 1个,你能办得到么?减少两个呢?44. 所谓闭折线,就是一些线段首尾相接构成一个回路.比如五角星,它是一个有5条边的闭折线,并且它的 5条边互相相交,共有5个交点(不包括线段的端点交点). 请问:一个有 6 条边的闭折线,它的 6 条边之间最多可以有多少个交点(不包括线段的端点交点)?45. 如图 6,将正面为白色,背面为红色,面积为 105 的长方形彩纸背面向正面折起一部分,使这部分重合到彩纸,这时,白色彩纸的面积只剩下了原来的0.2倍,求被折起的这部分(阴影部分)的面积.46. 如图 7,长方形 ABCD 中,△ABP 的面积为 30,△CDQ 的面积为 35,求阴影部分的面积.47. 如图 8,8边形的 8个角都是 135°.已知 AB=EF,BC=20,DE=10,GF=30,求AH的长.48. 如图 9,四边形 ABCD 是一个正方形,梯形 AEBD 的面积是 26,△AOE 的面积比△BOD的面积小 10,求正方形的边长.49. 如图 10,直角梯形 ABCD 中,DF⊥BC,AB=10,DE 的长度是 EF 的 4 倍,阴影部分的面积为90. 求梯形ABCD的面积.50. 如图 11,在梯形 ABCD中,AB=15,CD=5,梯形的面积为80,求△AOB的面积.51. 如图 12,过平行四边形 ABCD 的一点 P 作边的平行线 EF,GH,若平行四边形BEPH的面积为 4,平行四边形PFDG的面积为7,求△PAC 的面积.52. 如图 13,△ABC 中,试在AB上取点E,在AC 上取点F,D,连接 EF,ED,BD,使得△AEF,△EDF,△BDE,△BCD 的面积都相等(说出一种方法即可,但要证明其正确性).53. 如图 14(a)边长分别为 13,5 的两个正方形叠放在一起,两个正方形部的阴影部分的面积差为M. 如图14(b)边长分别为15, 9的两个正方形叠放在一起,两个正方形部的阴影部分的面积差为 N. 试比较 M与N 的大小.54. 在边长是 2米的等边三角形任意丢放 5颗小石子,则总有两颗小石子的距离不大于1米,请说出理由.55. 大伯利用一堵旧墙 AB,用长 50m 的篱笆围成一个留有 1m 宽的门的梯形场地CDEF(CD∥EF),如图15所示.若DE的长为 10m,则梯形场地 CDEF的最大面积是多少?56. 如图 16,ABCD 是正方形,AEGD,EFHG,FBCH 都是长方形,若图 16 中所有长方形(含正方形)的周长之和为190,EF=5,求正方形ABCD的面积.57. 用2017 个等腰直角三角形能不能拼成一个正方形? 请说明理由. (注:等腰直角三角形不要求一样大).、58. 一只乌鸦从其鸟巢飞出,飞向其巢北10 千米东7千米的A地,在 A地它发现有一个稻草人,所以就转向巢北 4 千米东 5 千米的 B 地飞去,在 B 地吃了一些谷物后立即返巢,其所飞的途径构成了一个三角形,这个三角形的面积为多少平方千米?59. 图 17 是一个正方体纸盒的展开图,当折叠成纸盒时,与点 1 重合的点的编号有哪些?60. 一组积木组成的图形,从正面看是,从侧面看是,则(1) 这组积木最少是用多少块正方体积木摆出来的?(2) 这组积木最多是用多少块正方体积木摆出来的?61. 甲、乙、丙在猜一个完全平方的两位数.甲说:它的因数个数为奇数,而且它比90大.乙说:它是奇数,而且它比 80小.丙说:它是偶数,而且它比 100小.如果他们三个人每个人都有半句真话,半句假话,那么这个数是多少?62. 如图 18,三根绳子系在一起,现在要在绳子的某处点火,如果每分钟火燃烧的距离是1,那么至少需要几分钟才能烧光这些绳子?63. 已知“西门鸡翅”的价格是3元钱2个鸡翅,“好伦哥”的价格是20元自助餐(无论吃多少个鸡翅都是 20 元),请根据图 19 中的对话判断,小笨至少能吃多少个鸡翅?64. 小笨得到了一笔压岁钱,但却忘了具体有多少钱. 他只记得这个三位数的各位数字之和是17,其中十位数字比个位数字大 1. 如果把这个三位数的百位数字与个位数字对调,得到一个新的三位数,则新的三位数比原三位数大 198. 请你帮小笨算算,这笔压岁钱有多少元?65. 某次考试共有 12 道判断题.小聪划了 7 个钩和 5 个叉,结果对了 8 道;小笨划了 3 个钩和9 个叉,结果对了 10 道;大壮一道不会,索性全部打叉,那么他至少可以蒙对多少道题?66. 如图 20,在空格填入数字 1~4,使得每行、每列和每个粗线围成的区域里数字都是1~4恰好各一个,若M+N>4,则 M× N 的值是多少?67. 有 61 个人坐成一横排.首先,正中间的一个人站起来,然后,按下述方法大家都或坐或站:(1) 如果邻座的人站起来,那么1秒钟后自己也站起来;(2) 站起1秒钟后坐下;(3) 如果左右邻座的人都是站着的,那么即使过了 1秒钟,自己仍然坐着.那么最初的那个人站起7秒钟后,有几个人站着?68. 某学生俱乐部有 11 个成员,他们的名字分别是 A~K.这些人分为两派,一派人总说实话,另一派人总说谎话.某日,老师问:“11 个人里面,总说谎话的有几个人?”那天,J 和K休息,余下的9个人这样回答:那么这个学生俱乐部的 11 个成员中,总说谎话的有多少个人?69. 某单位空降一名总经理,五位职员了解了这位经理的一些情况,现列表如下:这五位职员了解的情况,每人只有1项是正确的,请判定该经理的情况.70. 班长小英让 x 名同学去种少于 100棵的树苗.若每人种7棵,则余下 5棵;若每人种8棵,则有1 人只须种6棵. 求:(1)人数x; (2)树苗的棵数.71. 全家四口人,父亲比母亲大 3岁,姐姐比弟弟大 2岁. 4年前他们全家的年龄之和是58岁,而现在是 73岁. 问现在母亲的年龄是多少岁?72. 有一根木棍有三种刻度,第一种刻度将木棍分成 10 等份,第二种刻度将木棍分成12等份,第三种刻度将木棍分成15等份.如果沿每条刻度线将木棍锯断,请问木棍共被锯成多少段?73. 某快递公司已囤积部分快件,但仍有快件不断运来,公司决定用快递专车将快件分给客户,若 9 辆车发货,12 小时运完;若用 8 辆车发货,16 小时可以运完. 问:如果先用6 辆车运,3小时后需再增加几辆车,再过5小时可以运完?74. 10 点多的某个时刻,小明发现 1 分钟后表的时针与 1 分钟前表的分针夹角是180°,那么现在是 10点几分?75. 三堆苹果共 48 个. 先从第一堆中拿出与第二堆个数相等的苹果放入第二堆,再从第二堆中拿出与第三堆个数相等的苹果放入第三堆,最后又从第三堆中拿出与第一堆个数相等的苹果放入第一堆,这时三堆苹果数恰好相等.第一堆苹果原来有多少个?76. 甲、乙共有 26 颗糖.甲先拿走乙的一半,乙发现后,也拿走了甲的一半. 甲不服气,又偷偷拿了乙 5颗糖,此时甲比乙多 2颗,问:乙刚开始时有多少颗糖果?77. 甲、乙两车同时从 A,B两地相向而行,在距A地70千米处第一次相遇.各自到达对方出发地后立即返回,途中又在距 A 地 50 千米处相遇. 问:A,B 两地相距多少千米?78. 一列火车速度不变地驶过长为 600米的铁路桥需 1分钟,以相同的速度完全穿过长为2200米的隧道需要 3分钟,问:火车长多少米? (从车头上桥到车尾离桥即为完全驶过铁路桥)79. 华从家到学校上课,先用每分钟 80 米的速度走了 3 分钟,发现这样走下去将迟到3分钟;于是她就改用每分钟 110米的速度前进,结果提前了 3分钟到校.华家离学校有多远?80. 有 A,B,C 三辆车同时从同一地点出发,沿同一条公路追赶前面的一个骑车人,这三辆车分别用 6分钟、10 分钟、12 分钟追上骑车人.现在知道 A车每小时行24 千米,B车每小时行 20千米,那么,C 车每小时行多少千米?81. 某人沿着电车道旁的便道以 4.5千米每小时的速度步行,每14.4 分钟有一辆电车迎面开过,每 24 分钟有一辆电车从后面追过来,如果电车按相等的时间间隔以同一速度不停的往返运行,问:电车发车间隔是多少分?82. 星期六小王去球馆打球,去时发现家中的钟没电了,于是换上电池,把钟暂时调整到 8 时整,到球馆时球馆的钟刚好是 8 时整,打球到 11 时整,他以原速度回家发现家中的钟刚好是 12 时整,小王根据这些时间关系再次调整了时间,如果小王在路上的速度是 60米/分钟,请问:(1) 从家到球馆的路程是多少米?(2) 小王到家的准确时间是几点?83. 某汽车从 A 地开往 B 地,如果在计划行驶时间的前一半时间每小时行驶 30千米,而后一半时间每小时行驶 50千米,则按时到达;但汽车以每小时行驶 40千米的速度从A地行驶至离 A,B 中点还差 40 千米的地方发生故障,而停车检修半小时,此后以50 千米每小时的速度行驶,仍按时到达B地,问:(1) 原计划时间是几小时?(2) A,B两地的距离是多少千米?84. 甲、乙两名同学从山脚开始爬山,到达山顶后立即下山,在山脚和山顶之间不断往返运动. 已知山坡长 360 米,甲上山的速度是乙上山的速度的 1.5 倍,并且甲乙下山的速度是各自上山速度的 1.5 倍. 当甲第三次到达山顶时,乙所在的位置距山顶多少米?85. 熊大和熊二清晨起床后去学校的环形跑道上跑步锻炼,已知环形跑道的一周是 400 米,两只熊分别在相距 80 米的 A,B 两处同时跑,熊大每秒跑 3 米,熊二每秒跑2米,那么熊大和熊二几秒后第一次相遇?86. 甲、乙二人在一条相距 20 千米的平直公路的两处同时同向骑自行车(时速不超过 60 千米)前进,一小时后两人相距 15 千米,已知乙的时速比甲的时速的 2倍少10 千米,求甲,乙二人的时速.87. 加工一批零件,如果甲先做4 小时,乙再加入一起做,完成时甲比乙多做 400个,如果乙先做 4 小时,甲再加入一起做,完成时甲比乙多做 40 个. 如果一开始甲乙就一起做,那么,完成时甲比乙多做多少个?88. 猴子 A,B 一起上山摘桃子,猴子 B 单独摘完需要 50 天,如果猴子 A 第一天摘,猴子B第二天摘,这样交替摘,恰好整天数可摘完. 如果猴子 B 第一天摘,猴子 A 第二天摘,这样交替摘,恰好比上次轮流的方法多用半天摘完,那么猴子A单独摘完需要多少天?89. 一个玻璃容器里所装的糖水中含有10克糖,再倒入浓度为5%的糖水200克,配成浓度为2.5%的糖水. 那么原来这个玻璃容器的水有多少克?90. 用黑、白两种颜色的皮块缝制而成的足球,黑色皮块是正五边形,白色皮块是正六边形,若一个球上共有黑、白皮块 32 块,则(1) 黑色皮块有多少块?(2) 白色皮块有多少块?91. 小聪与小笨一起爬楼梯上楼,小聪家住 5层,小笨算了一下,自己的速度必须是小聪的2倍,这样才可以与小聪同时到达各自家中,那么小笨家住几层?92. 一个牧民买了一头母羊,每年能生 2只公羊, 4只母羊,每只小母羊两年后,又可以每年生6只羊,其中2只公羊,4只母羊.这样从今年开始到第 4年底,一共有多少只羊?93. 一辆长途汽车的起点是甲站,终点是丙站,中途停靠乙站. 从甲站到乙站和从乙站到丙站的票价都是 2元,而从甲站到丙站的票价是 3元,一天这辆长途汽车离开甲站时载有 45 名乘客,到了乙站有 12 人下车,19 人上车,那么该长途汽车这一天的车票收入是多少元?94. 甲、乙两人共带 90 千克行坐飞机旅行,机场规定:每人所带行重量不超过规定重量免费,超出部分重量按标准收费.两人分开带行分别收费是 16.8元和13.2 元;如果由一人带行就要收 42元.问:免费规定重量是不超过多少千克?95. 大壮加工一批产品,他每加工出一件正品,得报酬0.75元,每加工出一件次品,罚款1.50元,这天他加工的正品是次品的 7倍,得到11.25 元的报酬. 那么他这天加工出几件次品?96. 一个工人与用人单位签订了一个月的短期合同,双方约定,每工作一天得 80元,不上班不但没工资,且每天要倒扣10元.月末结账时,该工人领到工资 2030元,问这个工人工作了多少天?97. 顾客和店主有如下对话:顾客:老板,这件商品多少元?店主:这件商品五折减 5角和六折减6角的结果一样.顾客:按“五折减5 角”的优惠价买可以么?店主:不行!顾客:按“九折减9 角”的优惠价来买可以吗?店主:不行!问:(1) 这件商品的单价是多少?(2) 店主为什么坚持不卖?98. 小聪赶着一头猪到山外的生猪收购站去卖,过秤知猪重150斤,他和收购站的工作人员有如下对话:收购员:你这头猪肚子这么大又这么重,是不是故意让猪吃了很咸的猪食,然后大量喝水造成的?不收!小聪:我们家有诚信的家风,绝不会这样!请收购吧,我走了很远的山路才到这里.收购员:如果马上收购,猪的重量要打九折,如果你明天早上来,当面再称猪的重量,收购价提高两成五,两种选择由你确定!请帮助小聪作出选择,并说明理由.99. 一种商品,甲店:“买四赠一”,乙店:“优惠”,如果只从经济方面考虑,你选择去哪家商店?100. 有27位客人来某厂参观学习,厂领导派车去火车站接人,厂里有两种车子:可乘 3 人(司机除外)的小轿车和可乘 7 人(司机除外)的面包车,若要求车子全都满载,请确定派车的方案.参考答案1. 02. 13. 304. 105. 5.56. 392,5767. 358. 不会9. 12710. 3311. 3512. 813. 50214. 615. 18616. 1317. 3518. 40 或4519. 15020. 120321. 13822. 123. 9 24. 425. 4或 526. 5427. 2,5,1928. 4829. 3630. 21031. 20232. 47,3733. 24,634. 2835. 19636. 837. 2438. 31,2739. 23,1140. 1641. 360,10842. 17543. 10,可以44. 745. 4246. 6547. 2048. 649. 168.7550. 4551. 1.552. 略53. M = N54. 略55. 20556. 10057. 可以58. 1159. 2, 660. 3,961. 8162. 2163. 1464. 47665. 766. 967. 868. 969. 姓黄,男性,年薪240.万元,硕士学历70. 7,5471. 3172. 2873. 874. 2375. 2276. 1677. 13078. 20079. 2000 80. 1981. 1882. 1800,11:3083. 3,12084. 12085. 32086. 15,20;或5,087. 22088. 2589. 59090. 12,2091. 992. 9793. 16194. 2095. 396. 2697. 1元.98. 略99. 乙100. 9 辆小车或者 2 辆小车 3 辆面包车。


第十二届小学 希望杯 全国数学邀请赛参考答案及评分标准五年级㊀㊀第2试一㊁填空题(每小题5分㊂其中第4题,每空2.5分㊂)题号123456789101112答案12619102014;40266808.251569.7517284813㊀㊀二㊁解答题13.(1)最初,圆周上有3个数㊂第1次操作后,圆周上有3+3=6(个)数;第2次操作后,圆周上有6+6=12(个)数;第3次操作后,圆周上有12+12=24(个)数㊂(8分)(2)每次操作,新增的数是原来相邻的两个数的和,而原来的数各被加了2次,则新增的数的和是原来的数的和的2倍,即操作后圆周上的数的和是原来的3倍㊂最初,圆周上的3个数的和是1ˑ3=3㊂第1次操作后,圆周上的数的和是3ˑ3=9;第2次操作后,圆周上的数的和是3ˑ9=27;第3次操作后,圆周上的数的和是3ˑ27=81㊂(15分)14.(1)甲走一圈用360ː30=12(分),丙走一圈用㊀360ː90=4(分)㊂12和4的最小公倍数是12,所以,12分钟后,甲㊁丙第一次同时回到出发点㊂(5分)(2)丙走一圈用360ː50=7.2(分)㊂被12,7.2,4除,商都是大于零的整数,满足此条件的被除数最小是36㊂所以,36分钟后,三人第一次同时回到出发点㊂(10分)(3)当三人第一次同时到达同一地点时,他们各自走过的路程除以360所得的余数相同㊂设三人走了x 分钟,根据同余性质,有360∣(50x -30x ),18∣x ;360∣(90x -50x ),9∣x ;360∣(90x -30x ),6∣x ㊂18,9,6的最小公倍数是18㊂所以,18分钟后三人第一次同时到达同一地点㊂(15分)15.解法1㊀因为胜者加分,负者减同样的分,所以两队积分的和不变㊂(5分)若甲队胜,则甲队的积分是乙队的3倍,可知两队的积分和是4的倍数;若乙队胜,则甲队的积分是乙队的2倍,可知两队的积分和也是3的倍数㊂所以,两队的积分和是3ˑ4=12的倍数,即可能是12,24,36,48分㊂讨论如下:(10分)(1)两队的积分和是12分在甲队胜的情况下,甲队的积分是12ː4ˑ3=9(分);在乙队胜的情况下,甲队的积分是12ː3ˑ2=8(分),那么,本场比赛加分或减分的分值是(9-8)ː2=0.5(分),不符合题意㊂(2)两队的积分和是24分在甲队胜的情况下,甲队的积分是24ː4ˑ3=18(分);在乙队胜的情况下,甲队的积分是24ː3ˑ2=16(分),那么,本场比赛加分或减分的分值是(18-16)ː2=1(分),赛前甲队的积分是18-1=17(分),乙队的积分是24-17=7(分)㊂(3)两队的积分和是36分在甲队胜的情况下,甲队的积分是36ː4ˑ3=27(分),在乙队胜的情况下,甲队的积分是36ː3ˑ2=24(分),那么,本场比赛加分或减分的分值是(27-24)ː2=1.5(分),不符合题意㊂(4)两队的积分和是48分在乙队胜的情况下,甲队的积分是48ː3ˑ2=32(分),甲队赛前积分大于32分,不符合题意㊂综上可知,赛前甲队㊁乙队的积分分别是17分和7分㊂(15分)解法2㊀设甲队赛前积分为x分,乙队赛前积分为y分,本场比赛加分或减分的分值为n分(x,y,n都是整数)㊂根据题设条件,得x+n=3(y-n),①x-n=2(y+n),②(8分)①-②,得2n=3y-3n-2y-2n,解得y=7n,x=17n㊂(10分)因为赛前两队的积分都少于25分,所以n 只能取1㊂即赛前甲队积分为17分,乙队积分为7分㊂(15分)16.甲每秒游100ː200=0.5(米),乙每秒游100ː160=0.625(米),乙每秒比甲多游0.625-0.5=0.125(米),乙第1次追上甲,用40ː0.125=320(秒),(5分)在这个时间内,甲游了320ˑ0.5=160(米),还剩1000-160-40=800(米);乙第2次追上甲(距离差是100米),用100ː0.125=800(秒),(10分)在这个时间内,甲游了800ˑ0.5=400(米),此时,甲还剩800-400=400(米),到此,可知乙还可再追上甲1次㊂综上可知,甲被乙追上3次㊂(15分)。
第十届小学“希望杯”全国数学邀请赛五年级第1试2012年03月11日星期日1. 计算:1.2×67+6.7×88=2. 计算:21.49+52.37-0.4+5.51-11.37-6.6=3. 用1,2,3,4,5和+,-,×,÷组合成一个算式(不使用括号),计算结果最大是()。
4. 一件商品,对原价打八折和打六折的售价相差4.8元,那么这件商品的原价是()元。
5. 将252块巧克力,294盒饼干,336袋牛奶分成相同的份数,并且都没有余数,那么最多可以分成()份。
6. 若8只羊一星期要吃168千克饲料,一头牛的食量是一只羊的食量的2.8倍,那么,200只羊和180头牛一个月(按30天计)要吃()千克饲料。
7. 图1中,阴影面积最大的图形是(),阴影面积最小的图形是()。
(填序号)、8.一个两位数,将它的十位数字和个位数字对调,得到的数比原来的数大18,这样的两位数有()个。
9.如图2,如果小数的愿望能够实现,那么它的身高平均每年要增长到上一年的()倍。
10.两个不同的三位数被13除,若得到相同的余数,那么,这两个三位数的和最大是(),他们的差最大是()。
11.如图3,从左到右,在每列各选出一个框,组成算式(如:5×2+3),则有()种不同的结果。
12.A、B两地间有一条公路。
甲车从A驶到B,需60分钟;乙车从B驶到A,需120分钟。
若甲、乙两车分别从A、B两地同时出发,则在出发后()分钟相遇。
13.学校购买了数量相同的课桌和椅子,用小货车装运,每车装17张课桌和13把椅子。
装了若干车后,课桌剩9张,椅子剩77把。
那么,此时已经装了()车;按1桌1椅为1套,那么学校购买了()套课桌和椅子。
14.如图4,甲、乙、丙三个大小相同的杯子在桌面上一次排列,其中甲杯中盛满水,乙和丙是空杯。
现把水全部倒入相邻(左或右)的空杯中,那么,经过55次倒水后,有水的是()杯。
第一届小学“盼望杯”数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式可以成立:0.6+0.06+0.006+…=2002÷。
3.视察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的倍。
5.假如规定a※b =13×a-b÷8,那么17※24的最终结果是。
6.气象局对局部旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.是三角形的纸,=,图中的虚线是折痕,至少折次就可以得到8个一样的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任教师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园教师给几组小挚友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小挚友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比拟小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
15.长方形被分成了4个小长方形,图4中的数字是它们每个的面积,阴影局部的面积是。