正方形的性质及判定提高练习

~
第12题图 第13题图
13、边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′C′D′，两图叠成一个“蝶形风筝”（如图所示重叠部分），则这个风筝的面积是.
14、如图，边长为1的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′，边B′C′与DC交于点O，则四边形AB′OD的周长是.
（1）如图1，当四边形ABCD为正方形时，我们发现四边形EFGH是正方形；
如图2，当四边形ABCD为矩形时，请判断：四边形EFGH的形状是；（直接写出结果）
（2）如图3，当四边形ABCD为一般平行四边形时，设∠ADC= （0°＜ ＜90°），
① 试用含 的代数式表示∠HAE；
② 求证：HE=HG；
③ 四边形EFGH是什么四边形并说明理由．
（2）如图（2），若将正方形CGEF绕点C逆时针旋转 ，使得正方形CGEF对角线CE在正方形ABCD的边BC的延长线上， M为AE的中点。试问：（1）中探究的结论是否还成立若成立，请证明，若不成立，请说明理由。
》
图1 图2
!
17、以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连结这四个点，得四边形EFGH．
4、如图，等边△EDC在正方形ABCD内，连结EA、EB，则∠AEB＝°；∠ACE＝°.
—
5、已知正方形ABCD，以CD为边作等边△CDE，则∠AED的度数是°.
6、如图，四边形ABCD是正方形，E是边CD上一点，若△AFB经过逆时针旋转角θ（0°＜θ＜180°）后，与△AED重合，则θ值为°.
第6题图 第7题图 第8题图 第9题图
`
6、如图，在正方形ABCD中，△PBC、△QCD是两个等边三角形，PB与DQ交于M，BP与CQ交于E，CP与DQ交于F.求证：PM = QM.

专题5.3 正方形的性质与判定【十大题型】【浙教版】【题型1 正方形的性质（求角的度数）】 (1)【题型2 正方形的性质（求线段的长度）】 (3)【题型3 正方形的性质（求面积、周长）】 (4)【题型4 正方形的性质（探究数量关系）】 (6)【题型5 判定正方形成立的条件】 (10)【题型6 正方形判定的证明】 (12)【题型7 正方形的判定与性质综合】 (16)【题型8 探究正方形中的最值问题】 (19)【题型9 正方形在坐标系中的运用】 (20)【题型10 正方形中的多结论问题】 (23)【题型1 正方形的性质（求角的度数）】【例1】（2022春•建阳区期中）如图，在正方形ABCD中有一个点E，使三角形BCE是正三角形，求：（1）∠BAE的大小（2）∠AED的大小．【变式1-1】如图，已知正方形ABCD在直线MN的上方，BC在直线MN上，E是BC上一点，以AE为边在直线MN上方作正方形AEFG．（1）连接GD，求证：△ADG≌△ABE；（2）连接FC，观察并猜测∠FCN的度数，并说明理由．【变式1-2】（2022•武威模拟）如图，在正方形ABCD中，点E是对角线AC上的一点，点F在BC的延长线上，且BE＝EF，EF交CD于点G．（1）求证：DE＝EF；（2）求∠DEF的度数．【变式1-3】（2022春•新市区校级期末）如图，在给定的正方形ABCD中，点E从点B出发，沿边BC方向向终点C运动，DF⊥AE交AB于点F，以FD，FE为邻边构造平行四边形DFEP，连接CP，则∠DFE+∠EPC的度数的变化情况是（）A．一直减小B．一直减小后增大C．一直不变D．先增大后减小【题型2 正方形的性质（求线段的长度）】【例2】（2022春•牡丹江期末）如图，正方形ABCD的边长为10，点E，F在正方形内部，AE＝CF＝8，BE＝DF＝6，则线段EF的长为（）A．2√2B．4C．4−√2D．4+√2【变式2-1】（2022春•巴南区期末）如图，四边形ABCD是边长为4的正方形，点E在边CD上，且DE ＝1，作EF∥BC分别交AC、AB于点G、F，P、H分别是AG，BE的中点，则PH的长是（）A．2B．2.5C．3D．4【变式2-2】（2022•越秀区一模）将正方形ABCD与正方形BEFG按如图方式放置，点F、B、C在同一直线上，已知BG=√2，BC＝3，连接DF，M是DF的中点，连接AM，则AM的长是（）A．√102B．√3C．√132D．32【变式2-3】（2022春•吴中区校级期末）如图，在正方形ABCD中，AB＝4√5．E、F分别为边AB、BC的中点，连接AF、DE，点N、M分别为AF、DE的中点，连接MN，则MN的长度为．【题型3 正方形的性质（求面积、周长）】【例3】（2022春•鄞州区期末）有两个正方形A，B．现将B放在A的内部得图甲，将A，B构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为1和12，若三个正方形A和两个正方形B得图丙，则阴影部分的面积为（）A．28B．29C．30D．31【变式3-1】（2022春•工业园区校级期中）如图，四边形ABCD为正方形，O为AC、BD的交点，△DCE 为Rt△，∠CED＝90°，OE＝2√2，若CE•DE＝3，则正方形ABCD的面积为（）A．5B．6C．8D．10【变式3-2】（2022•台州）如图，在正方形ABCD中，AB＝3，点E，F分别在CD，AD上，CE＝DF，BE，CF相交于点G．若图中阴影部分的面积与正方形ABCD的面积之比为2：3，则△BCG的周长为．【变式3-3】（2022•江北区一模）如图，以Rt△ABC的各边为边分别向外作正方形，∠BAC＝90°，连结DG，点H为DG的中点，连结HB，HN，若要求出△HBN的面积，只需知道（）A．△ABC的面积B．正方形ADEB的面积C．正方形ACFG的面积D．正方形BNMC的面积【题型4 正方形的性质（探究数量关系）】【例4】（2022秋•中原区校级月考）如图，线段AB＝4，射线BG⊥AB，P为射线BG上一点，以AP为边作正方形APCD，且点C、D与点B在AP两侧，在线段DP上取一点E，使∠EAP＝∠BAP，直线CE 与线段AB相交于点F（点F与点A、B不重合）．（1）求证：△AEP≌△CEP；（2）判断CF与AB的位置关系，并说明理由；（3）请直接写出△AEF的周长．【变式4-1】（2022春•雁塔区校级期末）在正方形ABCD中，∠MAN＝45°，该角可以绕点A转动，∠MAN的两边分别交射线CB，DC于点M，N．（1）当点M，N分别在正方形的边CB和DC上时（如图1），线段BM，DN，MN之间有怎样的数量关系？你的猜想是：，并加以证明．（2）当点M，N分别在正方形的边CB和DC的延长线上时（如图2），线段BM，DN，MN之间的数量关系会发生变化吗？证明你的结论．【变式4-2】（2022春•莆田期末）如图，已知正方形ABCD中，E为CB延长线上一点，且BE＝AB，M、N分别为AE、BC的中点，连DE交AB于O，MN交，ED于H点．（1）求证：AO＝BO；（2）求证：∠HEB＝∠HNB；（3）过A作AP⊥ED于P点，连BP，则PE−PA的值．PB【变式4-3】（2022春•鼓楼区校级期中）如图，正方形ABCD的对角线相交于点O．点E是线段DO上一点，连接CE．点F是∠OCE的平分线上一点，且BF⊥CF与CO相交于点G．点H是线段CE上一点，且CO＝CH．（1）若OF＝5，求FH的长；（2）求证：BF＝OH+CF．【题型5 判定正方形成立的条件】【例5】（2022春•海淀区校级期中）已知四边形ABCD为凸四边形，点M、N、P、Q分别为AB、BC、CD、DA上的点（不与端点重合），下列说法正确的是（填序号）．①对于任意凸四边形ABCD，一定存在无数个四边形MNPQ是平行四边形；②如果四边形ABCD为任意平行四边形，那么一定存在无数个四边形MNPQ是矩形；③如果四边形ABCD为任意矩形，那么一定存在一个四边形为正方形；④如果四边形ABCD为任意菱形，那么一定存在一个四边形为正方形．【变式5-1】（2022春•岳麓区校级月考）如图，E、F、G、H分别是AB、BC、CD、DA的中点．要使四边形EFGH是正方形，BD、AC应满足的条件是．【变式5-2】（2022春•汉寿县期中）如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F在AC 上，且OE＝OF，连接DE并延长至点M，使DE＝ME，连接MF，DF，BE．（1）当DF＝MF时，证明：四边形EMBF是矩形；（2）当△DMF满足什么条件时，四边形EMBF是正方形？请说明理由．【变式5-3】（2022春•沛县期中）已知在△ABC中，D为边BC延长线上一点，点O是边AC上的一个动点，过O作直线MN∥BC，设MN与∠BCA的平分线相交于点E，与∠ACD的平分线相交于点F．（1）求证：OE＝OF；（2）试确定点O在边AC上的位置，使四边形AECF是矩形，并加以证明．（3）在（2）的条件下，且△ABC满足条件时，矩形AECF是正方形？．【题型6 正方形判定的证明】【例6】（2022春•虹口区期末）如图，在四边形ABCD中，AB∥CD，AD＝CD，E是对角线BD上的一点，且AE＝CE．（1）求证：四边形ABCD是菱形；（2）如果AB＝BE，且∠ABE＝2∠DCE，求证：四边形ABCD是正方形．【变式6-1】（2022春•宜城市期末）如图，四边形ABCD是平行四边形，连接对角线AC，过点D作DE ∥AC与BC的延长线交于点E，连接AE交DC于F．（1）求证：BC＝CE；（2）连接BF，若∠DAF＝∠FBE，且AD＝2CF，求证：四边形ABCD是正方形．【变式6-2】（2022秋•市南区期末）已知：在平行四边形ABCD中，分别延长BA，DC到点E，H，使得BE＝2AB，DH＝2CD．连接EH，分别交AD，BC于点F，G．（1）求证：AF＝CG；（2）连接BD交EH于点O，若EH⊥BD，则当线段AB与线段AD满足什么数量关系时，四边形BEDH 是正方形？【变式6-3】（2022•上海）已知：如图，四边形ABCD中，AD∥BC，AD＝CD，E是对角线BD上一点，且EA＝EC．（1）求证：四边形ABCD是菱形；（2）如果BE＝BC，且∠CBE：∠BCE＝2：3，求证：四边形ABCD是正方形．【题型7 正方形的判定与性质综合】【例7】（2022•威海）如图1，在正方形ABCD中，E，F，G，H分别为边AB，BC，CD，DA上的点，HA＝EB＝FC＝GD，连接EG，FH，交点为O．（1）如图2，连接EF，FG，GH，HE，试判断四边形EFGH的形状，并证明你的结论；（2）将正方形ABCD沿线段EG，HF剪开，再把得到的四个四边形按图3的方式拼接成一个四边形．若正方形ABCD的边长为3cm，HA＝EB＝FC＝GD＝1cm，则图3中阴影部分的面积为cm2．【变式7-1】（2022•萧山区模拟）如图，P为正方形ABCD内的一点，画▱P AHD，▱PBEA，▱PCFB，▱PDGC，请证明：以E，F，G，H为顶点的四边形是正方形．【变式7-2】（2022•萧山区模拟）已知：如图，边长为4的菱形ABCD的对角线AC与BD相交于点O，若∠CAD＝∠DBC．（1）求证：四边形ABCD是正方形．（2）E是OB上一点，BE＝1，且DH⊥CE，垂足为H，DH与OC相交于点F，求线段OF的长．【变式7-3】（2022春•潜山市期末）如图，已知四边形ABCD为正方形，AB＝3√2，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．（1）求证：矩形DEFG是正方形；（2）探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．【题型8 探究正方形中的最值问题】【例8】（2022春•沙坪坝区校级月考）如图，在正方形ABCD中，M，N是边AB上的动点，且AM＝BN，连接MD交对角线AC于点E，连接BE交CN于点F，若AB＝3，则AF长度的最小值为．【变式8-1】（2022•泰山区一模）如图，M、N是正方形ABCD的边CD上的两个动点，满足AM＝BN，连接AC交BN于点E，连接DE交AM于点F，连接CF，若正方形的边长为2，则线段CF的最小值是（）A．2B．1C．√5−1D．√5−2【变式8-2】（2022•青山区模拟）已知矩形ABCD，AB＝2，AD＝4AB＝8，E为线段AD上一动点，以CE 为边向上构造正方形CEFG，连接BF，则BF的最小值是．【变式8-3】（2022•郧阳区模拟）如图，P A=2√2，PB=4√2，以AB为边作正方形ABCD，使得P、D两点落在直线AB的两侧，当∠APB变化时，则PD的最大值为．【题型9 正方形在坐标系中的运用】【例9】（2022春•市中区期末）在平面直角坐标系中，对于两个点P、Q和图形W，如果在图形W上存在点M、N（M、N可以重合）使得PM＝QN，那么称点P与点Q是图形W的一对平衡点．已知正方形的边长为2，一边平行于x轴，对角线的交点为点O，点D的坐标为（2，0）．若点E（x，2）与点D是正方形的一对平衡点，则x的取值范围为（）A．﹣3≤x≤3B．﹣4≤x≤4C．﹣2≤x≤2D．﹣5≤x≤5【变式9-1】（2022秋•永新县期末）如图，在平面直角坐标系中，四边形ABCD的顶点坐标分别是A（﹣2，0）、B（0，﹣2）、C（2，0）、D（0，2），求证：四边形ABCD是正方形．【变式9-2】（2022春•顺城区期末）如图，在平面直角坐标系xOy中，直线OC：yOC＝3x与直线AC：yAC＝﹣x+8相交于点C（2，6）．（1）点M从点O出发以每秒1个单位长度的速度沿x轴向右运动，点N从点A出发以每秒3个单位长度的速度沿x轴向左运动，两点同时出发．分别过点M，N作x轴的垂线，分别交直线OC，AC于点P，Q，请你在图1中画出图形，猜想四边形PMNQ的形状（点M，N重合时除外），并证明你的猜想；（2）在（1）的条件下，当点M运动秒时，四边形PMNQ是正方形（直接写出结论）．【变式9-3】（2022•河南模拟）如图，正方形OABC 中，点A （4，0），点D 为AB 上一点，且BD ＝1，连接OD ，过点C 作CE ⊥OD 交OA 于点E ，过点D 作MN ∥CE ，交x 轴于点M ，交BC 于点N ，则点M 的坐标为（ ）A ．（5，0）B ．（6，0）C ．（254，0）D ．（274，0） 【题型10 正方形中的多结论问题】【例10】（2022春•慈溪市期末）如图，正方形ABCD 中，点P 为BD 延长线上任一点，连结P A ，过点P 作PE ⊥P A ，交BC 的延长线于点E ，过点E 作EF ⊥BP 于点F ．下列结论：（1）P A ＝PE ； （2）BD ＝2PF ；（3）CE =√2PD ； （4）若BP ＝BE ，则PF =(√2+1)DF ．其中正确的个数为（ ）A ．1B ．2C ．3D ．4【变式10-1】（2022春•渝中区校级期中）如图，正方形ABCD 的边长为a ，点E 在边AB 上运动（不与点A ，B 重合），∠DAM ＝45°，点F 在射线AM 上，且AF =√2BE ，CF 与AD 相交于点G ．连接EC 、EF 、EG ．下列结论：①∠ECF ＝45°；②△AEG 的周长为（1+√22）a ；③BE 2+DG 2＝EG 2；④当G 是线段AD的中点时，BE =13a ．正确的个数是（ ）A．1个B．2个C．3个D．4个【变式10-2】（2022秋•三水区月考）如图，正方形ABCD中，在AD的延长线上取点E，F，使DE＝AD，DF＝BD，连接BF分别交CD，CE于H，G，下列结论：①HF＝2HG；②∠GDH＝∠GHD；③图中有8个等腰三角形；④S△CDG＝S△DHF．其中正确的结论个数是（）A．1个B．2个C．3个D．4个【变式10-3】（2022春•玉林期末）如图，正方形ABCD中，点E在边CD上，过点A作AF⊥AE交CB的延长线于点F，连接EF，AG平分∠F AE，AG分别交BC、EF于点G、H，连接EG、DH．则下列结论中：①BF＝DE；②∠EGC＝2∠BAG；③AD+DE=√3DH；④DE+BG＝EH；⑤若DE＝CE，则CE：CG：EG＝3：4：5，其中正确的结论有．。

1.3正方形的性质与判定1、四边形ABCD中，AC、BD相交于点O，能判别这个四边形是正方形的条件是（）A. OA＝OB＝OC＝OD，AC⊥BDB. AB∥CD，AC＝BDC. AD∥BC，∠A＝∠CD. OA＝OC，OB＝OD，AB＝BC2、在正方形ABCD中，AB＝12cm，对角线AC、BD相交于O，则△ABO的周长是（）A. 12+122B. 12+62C. 12+2D. 24+623、如图，四边形ABCD是正方形，延长BC至点E，使CE＝CA，连结AE交CD•于点F，•则∠AFC的度数是（）．（A）150°（B）125°（C）135°（D）112．5°4、已知正方形的面积为4，则正方形的边长为________，对角线长为________．5、如左下图，四边形ABCD是正方形，△CDE是等边三角形，则∠AED＝______，∠AEB＝______．6、如右上图，四边形ABCD是正方形，△CDE是等边三角形，求∠AEB的度数.7、已知：如左下图，在正方形ABCD中，AE⊥BF，垂足为P，AE与CD交于点E，•BF与AD交于点F，求证：AE＝BF．8、如图，正方形ABCD，AB＝a，M为AB的中点，ED＝3AE，（1）求ME的长；（2）△EMC是直角三角形吗？为什么？9、如左下图，在正方形ABCD中，E、F、G、H分别在它的四条边上，且AE=BF=CG=DH.四边形EFGH是什么特殊的四边形，你是如何判断的？10、如右上图所示，E 是正方形ABCD 的对角线BD 上一点，EF ⊥BC ，EG ⊥CD ，垂足分别是F 、G ．试说明AE ＝FG ．11、以锐角△ABC 的边AC 、AB 为边向外作正方形ACDE 和正方形ABGF ，连结BE 、CF.（1）试探索BE 和CF 的关系？并说明理由。

（2）你能找到哪两个图形可以通过旋转而相互得到，并指出旋转中心和旋转角。

正方形性质及判定练习题正方形是一种特殊的四边形，具有一些独特的性质。

在本文档中，我们将介绍关于正方形的性质以及如何判定一个形状是否为正方形的练题。

1. 正方形的定义- 正方形是一个四边形，具有四条相等的边和四个相等的角。

- 每个角都是直角，即90度。

2. 正方形的性质- 边长：正方形的四条边长度相等。

- 角度：正方形的每个角都是直角，即90度。

- 对角线：正方形的对角线相等且垂直相交于中点。

3. 正方形的判定练题1. 练题1：给出一个形状的四条边长A、B、C、D，如何确定它是否为正方形？- 答案：如果A = B = C = D，并且角ABC和角BCD均为直角（90度），则该形状为正方形。

2. 练题2：给出一个形状的四个顶点坐标(Ax, Ay)，(Bx, By)，(Cx, Cy)，(Dx, Dy)，如何确定它是否为正方形？- 答案：计算四条边的长度AB、BC、CD、DA，并检查是否满足A = B = C = D的条件。

同时，计算角ABC、BCD、CDA、DAB是否均为90度。

3. 练题3：给出一个形状的四个顶点坐标(Ax, Ay)，(Bx, By)，(Cx, Cy)，(Dx, Dy)，如何确定它是否为正方形？如果无法使用角度判定，请给出其他方法。

- 答案：计算四条边的长度AB、BC、CD、DA，并检查是否满足A = B = C = D的条件。

同时，计算AB和CD的斜率，如果斜率为相反数且BC和DA的斜率为相反数，那么该形状为正方形。

通过掌握正方形的定义、性质以及判定练题，我们能够更好地理解和识别正方形。

练题的完成也有助于加深对正方形性质的掌握。

希望这份文档对您有所帮助！。

2021-2022学年北师大版九年级数学上册《1.3正方形的性质与判定》同步能力提升训练（附答案）1．如图，E为正方形ABCD的对角线上一点，四边形EFCG为矩形，若正方形ABCD的边长为4，则EG+GC的长为（）A．4B．8C．16D．322．如图是一个正方形和直角三角形的组合图形，直角三角形的斜边和一条直角边的长分别为10cm，8cm，则该正方形的面积为（）A．6cm2B．36cm2C．18cm2D．2cm23．正方形具有而菱形不一定具有的性质是（）A．四边相等B．对角线相等C．对角线互相垂直D．对角线互相平分4．如图，正方形ABCD中，点E是对角线BD上的一点，且BE＝AB，连接CE，AE，则∠DAE的度数为（）A．22.5°B．25°C．30°D．32.5°5．如图，将平行四边形ABCD的∠ABC变成直角，则平行四边形ABCD变成（）A．平行四边形B．矩形C．菱形D．正方形6．正方形、菱形、矩形、平行四边形共同具有的性质是（）A．对角线相等B．对角线相互平分C．对角线相互垂直D．对角线相互垂直平分7．如图，在正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，连接AC，CF，那么AF的长是（）A．B．2C．3D．28．下列说法错误的是（）A．对角线垂直且互相平分的四边形是菱形B．对角线相等的平行四边形是矩形C．对角线相等且垂直的四边形是正方形D．一组对边平行且相等的四边形是平行四边形9．如图，正方形ABCD的面积是2，E，F，P分别是AB，BC，AC上的动点，PE PF的最小值为（）A．3 B．2C．2 D．110．如图，正方形ABCD的边长为4，点E在CD的边上，且DE=1，△AFE与△ADE关于AE 所在的直线对称，将△ADE按顺时针方向绕点A旋转90°得到△ABG，连接FG，则线段FG 的长为（）A．4 B．42C．5 D．611．如图，已知四边形ABCD是平行四边形，下列结论中正确的是（）A．当AC＝BD时，它是正方形B．当AC⊥BD时，它是矩形C．当∠ABC＝90°时，它是菱形D．当AB＝BC时，它是菱形12．下列条件中能判断一个四边形是正方形的是（）A．对角线互相垂直且相等B．一组对边平行，另一组对边相等且有一个内角为90度C．对角线平分每一组对角D．四边相等且有一个角是直角13．如图，将正方形OACD放在平面直角坐标系中，O是坐标原点，点D的坐标为（3，4），则点A的坐标为．14．菱形ABCD中，AD＝4，∠DAB＝60°，E、F、G、H分别是AD、AB、BC、CD上的点，且DH＝FB，DE＝BG，当四边形EFGH为正方形时，DH＝．15．如图，正方形ABCD的边长为12，对角线AC、BD相交于点O，E是AC上一点，连接BE并延长交正方形ABCD的边于点F，若OE＝3，则CF＝．16．如图，四边形OBCD是正方形，O，D两点的坐标分别是（0，0），（0，5），点C在第一象限，则点C的坐标是．17．如图，正方形ABCD中，点P在边AD上，PE⊥AC于点E，PF⊥BD于点F，AC＝m，PE+PF＝n，则m，n满足的数量关系是．18．已知：如图，在矩形ABCD中，E、F分别是边CD、AD上的点，AE⊥BF，且AE＝BF．（1）求证：矩形ABCD是正方形；（2）联结BE、EF，当线段DF是线段AF与AD的比例中项时，求证：∠DEF＝∠ABE．19．如图，四边形ABCD是正方形，对角线AC、BD相交于点F，∠E＝90°，ED＝EC．求证：四边形DFCE是正方形．20．如图，在正方形ABCD中，E、F、G、H分别是各边上的点，且AE＝BF＝CG＝DH．求证：（1）△AHE≌△BEF；（2）四边形EFGH是正方形．21．如图，在四边形ABDE中，AD与BE相交于点O，OA＝OB＝OE＝OD，AB＝BD．（1）求证：四边形ABDE是正方形；（2）若∠ACB＝90°，连接OC，OC＝6，AC＝5，求BC的长．22．如图，在Rt△ABC中，∠ACB＝90°，CD平分∠ACB，过点D分别作DE⊥BC，DF ⊥AC，垂足分别为E，F．（1）证明：四边形DECF为正方形；（2）若AC＝6cm，BC＝8cm，求四边形DECF的面积．参考答案1．解：∵四边形ABCD是正方形，∴∠BDC＝45°，∴EG＝DG，∵四边形EFCG为矩形，∴EF＝GC，∴EF+EG＝GC+DG＝DC＝4，故选：A．2．解：如图所示：∵△ABE是直角三角形，AE＝8cm，BE＝10cm，∴AB＝（cm），∵四边形ABCD是正方形，∴正方形ABCD的面积＝AB2＝36（cm2），故选：B．3．解：菱形和矩形的性质合在一起得到了正方形．正方形具有而菱形不具有的性质即为矩形的特性，由矩形对角线相等满足条件．故选：B．4．解：∵四边形ABCD为正方形，∴∠ABD＝45°，∠BAD＝90°，∵BE＝AB，∴∠BAE＝∠BEA＝×（180°﹣45°）＝67.5°，∴∠DAE＝∠BAD﹣∠BAE＝90°﹣67.5°＝22.5°．故选：A．5．解：∵四边形ABCD是平行四边形，∠ABC＝90°，∴四边形ABCD是正方形，故选：B．6．解：平行四边形的对角线互相平分，而对角线相等、对角线相互垂直、对角线相互垂直平分不一定成立．故平行四边形、矩形、菱形、正方形都具有的性质是：对角线互相平分．故选：B．7．解：∵四边形ABCD和四边形CEFG为正方形，BC＝1，CE＝3，∴AB＝BC＝1，CE＝EF＝3，∠B＝∠E＝90°，∴AC＝＝，CF＝＝，∵AC、CF分别是正方形ABCD和正方形CEFG的对角线，∴∠ACG＝∠GCF＝45°，∴∠ACF＝90°，在Rt△ACF中，AF＝＝＝2．故选：D．8．解：A．对角线垂直且互相平分的四边形是菱形，正确，不合题意；B．对角线相等的平行四边形是矩形，正确，不合题意；C．对角线相等且垂直的平行四边形是正方形，原说法错误，符合题意；D．一组对边平行且相等的四边形是平行四边形，正确，不合题意．故选：C．MN AD交AB于点M，交CD于点N，如图所示：9．解：过点P作//四边形ABCD为正方形，∴⊥，MN AB⊥时取等号），∴（当PE ABPM PE⊥时取等号），PN PF（当PF BC∴==++，MN AD PM PN PE PF正方形ABCD的面积是2，2∴AD∴+2B．PE PF10．解:如图，连接BE，∵△AFE与△ADE关于AE所在的直线对称，∴AF=AD，∠EAD=∠EAF，∵△ADE按顺时针方向绕点A旋转90°得到△ABG，∴AG=AE，∠GAB=∠EAD，∴∠GAB=∠EAF，∴∠GAB+∠BAF=∠EAF+∠BAF，∴∠GAF=∠EAB，∴△GAF≅△EAB（SAS），∴FG=EB，∵四边形ABCD是正方形，∴BC=CD=AB=4，∵DE=1，∴CE=3，∴在Rt△BCE中，22+，345∴FG=5故选C11．解：∵四边形ABCD是平行四边形，∴当AC＝BD时，它是矩形，故选项A不符合题意；当AC⊥BD时，它是菱形，故选项B不符合题意；当∠ABC＝90°时，它是矩形，故选项C不符合题意；当AB＝BC时，它是菱形，故选项D符合题意；故选：D．12．解：对角线互相垂直、平分且相等的四边形是正方形，但是对角线互相垂直且相等的四边形不一定是正方形，如等腰梯形中的对角线就有可能垂直且相等，故选项A不符合题意；一组对边平行，另一组对边相等且有一个内角为90度的四边形不一定是正方形，如直角梯形，故选项B不符合题意；对角线平分每一组对角的四边形不一定是正方形，如菱形，故选项C不符合题意；四边相等且有一个角是直角的四边形是正方形，故选项D符合题意；故选：D．13．解：如图，过点A作AB⊥x轴于B，过点D作DE⊥x轴于E，∵四边形OACD是正方形，∴OA＝OD，∠AOD＝90°，∴∠DOE+∠AOB＝90°，又∵∠OAB+∠AOB＝90°，∴∠OAB＝∠DOE，在△AOD和△OCE中，，∴△AOB≌△ODE（AAS），∴AB＝OE，OB＝DE，∵点D的坐标为（3，4），点C在第二象限，∴点C的坐标为（﹣4，3）．故答案为：（﹣4，3）．14．解：过点E作AB的垂线分别交AB于N、交CD延长线于M，∵四边形EFGH为正方形，∴EH＝EF，∠HEF＝90°，∴∠MEH+∠NEF＝90°，∵∠NEF+∠EFN＝90°，∴∠MEH＝∠EFN，在△EMH与△FNE中，，∴△EMH≌△FNE（AAS），∴EM＝NF，EN＝MH，设MD＝x，在菱形ABCD中，AD＝4，∠DAB＝60°，∴∠ADM＝30°，∴MD＝DE，∴DE＝2x，EM＝＝x，∴AE＝4﹣2x，AN＝＝2﹣x，∴EN＝＝（2﹣x），∴NF＝x，HM＝（2﹣x），DH＝MH﹣MD＝2﹣x﹣x，∴AF＝2﹣x+x，∵AB＝CD，BF＝DH，∴AF＝CH＝2﹣x+x，∵DH+CH＝4，∴2﹣x+x+2﹣x﹣x＝4，解得：x＝﹣1，∴DH＝2﹣2．故答案为：2﹣2．15．解：∵正方形ABCD的边长为12，∴AC＝12，∴OA＝OC＝6，∵OE＝3，∴E点是OA或OC的中点，如图1，当E点是OA的中点时，过点E作NE⊥AB交AB于N，∴AE＝3，∴AN＝NE＝3，∵NE∥AF，∴AF＝4，∴DF＝8，∴CF＝4；如图2，当E为CO的中点时，过点E作EM⊥BC交BC于M，则EC＝3，∴EM＝MC＝3，∴BM＝9，∵EM∥FC，∴FC＝4；综上所述：FC的长为4或4．16．解：∵四边形OBCD是正方形，∴OB＝BC＝CD＝OD，∠CDO＝∠CBO＝90°，∵O，D两点的坐标分别是（0，0），（0，5），∴OD＝5，∴OB＝BC＝CD＝5，∴C的坐标为（5，5）．故答案为：（5，5）．17．解：∵四边形ABCD是正方形，∴∠CAD＝45°，AC⊥BD，AC＝2OA，∵PE⊥AC，PF⊥BD，∴△APE是等腰直角三角形，四边形PEOF是矩形，∴PE＝AE，PF＝OE，∴OA＝AE+OE＝PE+PF，∵AC＝m，PE+PF＝n，AC＝2OA，∴m＝2n．故答案为：m＝2n．18．证明：（1）∵四边形ABCD是矩形，∴∠BAD＝∠ADE＝90°，∴∠ABF+∠AFB＝90°，∵AE⊥BF，∴∠DAE+∠AFB＝90°，∴∠ABF＝∠DAE，在△ABF和△DAE中，，∴△ABF≌△DAE（AAS），∴AB＝AD，∴矩形ABCD是正方形；（2）由（1）可知，△ABF≌△DAE，∴AF＝DE，∴DF＝CE，∵∠FDE＝∠BCE＝90°，∴△FDE∽△BCE，∴∠DEF＝∠CEB，∵AB∥CD，∴∠ABE＝∠CEB，∴∠ABE＝∠DEF．19．解：∵四边形ABCD是正方形，∴∠FDC＝∠DCF＝45°，∵∠E＝90°，ED＝EC，∴∠EDC＝∠ECD＝45°，∴∠FCE＝∠FDE＝∠E＝90°，∴四边形DFCE是矩形，∵DE＝CE，∴四边形DFCE是正方形．20．证明：（1）∵四边形ABCD为正方形，∴AB＝BC＝CD＝DA，∠A＝∠B＝90°，又∵AE＝BF＝DH＝CG，∴AH＝BE＝CF＝DG，∴△AHE≌△BEF（SAS）；（2）在正方形ABCD中，AB＝BC＝CD＝AD，∵AE＝BF＝CG＝DH，∴AH＝DG＝CF＝BE，∵∠A＝∠B＝∠C＝∠D＝90°，∴△AEH≌△DHG≌△CGF≌△BFE（SAS），∴EF＝EH＝HG＝GF，∠EHA＝∠HGD，∴四边形EFGH是菱形，∵∠EHA＝∠HGD，∠HGD+∠GHD＝90°，∴∠EHA+∠GHD＝90°，∴∠EHG＝90°，∴四边形EFGH是正方形．21．解：（1）∵OA＝OB＝OE＝OD，∴四边形ABCD是平行四边形，AD＝BE，∴四边形ABDE是矩形，又∵AB＝BD，∴四边形ABDE是正方形．（2）如图所示，过O作OF⊥BC，过A作AM⊥OF，∵四边形ABDE为正方形，∴∠AOB＝90°，OA＝OB，∴∠AOM+∠BOF＝90°，又∠AMO＝90°，∴∠AOM+∠OAM＝90°，∴∠BOF＝∠OAM，在△AOM和△BOF中，，∴△AOM≌△BOF（AAS），∴AM＝OF，OM＝FB，又∵∠ACB＝∠AMF＝∠CFM＝90°，∴四边形ACFM为矩形，∴AM＝CF，AC＝MF＝5，∴OF＝AM＝CF，∴△OCF为等腰直角三角形，∵OC＝6，根据勾股定理得：CF2+OF2＝OC2，解得：CF＝OF＝6，∴FB＝OM＝OF﹣FM＝6﹣5＝1，∴BC＝CF+BF＝6+1＝7．22．（1）证明：∵DE⊥BC，DF⊥AC，∠ACB＝90°，∴∠DFC＝∠FCE＝∠DEC＝90°，∴四边形DECF是矩形，∴DF∥EC，∴∠FDC＝∠ECD，∵CD平分∠ACB，∴∠FCD＝∠ECD，∴∠FDC＝∠FCD，∴DF＝CF，∴四边形DECF是正方形；（2）解：∵四边形DECF是正方形，∴DF＝FC＝CE＝DE，设DF＝FC＝CE＝DE＝x，∵DF∥BC，∴x＝，即DF＝FC＝CE＝DE＝，∴四边形DECF的面积是×＝．。

初二正方形性质及判定练习题
形状与性质
正方形是一种特殊的四边形，具有以下性质：
1. 四条边相等：正方形的四条边的长度相等。

2. 四个角相等：正方形的四个角的大小都是90度。

3. 对角线相等：正方形的对角线长度相等。

4. 正方形是菱形：正方形的对角线相互垂直，且长度相等，因此也是菱形的一种特殊情况。

判定练题
以下是一些判定练题，帮助你巩固对正方形性质的理解：
1. 判断下列图形是否为正方形：
A. 
B. 
C. 
D. 
答案：A是正方形，B是正方形，C不是正方形，D不是正方形。

2. 若两个正方形的边长分别为4cm和6cm，哪个正方形的面积更大？
答案：边长为6cm的正方形面积更大，因为面积与边长的平方成正比。

3. 若一个正方形的对角线长度为10cm，求其边长。

答案：根据正方形的性质，对角线长度等于边长乘以√2，所以边长等于10cm除以√2，约为7.07cm。

4. 若一个四边形的边长均为5cm，四个角的大小均为90度，是否一定是正方形？
答案：不一定，虽然满足了长宽相等和角度为90度的条件，但没有保证对角线相等，因此不一定是正方形。

5. 若一个四边形的对角线相等，四个角的大小均为90度，是否一定是正方形？
答案：是的，根据这些条件可以确定该四边形是正方形，因为这些是正方形的定义性质。

以上是关于初二正方形性质及判定练习题的内容。

希望能够帮助你更好地理解和应用正方形的性质。

1、判断题:
(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形（
√
） ）
(3)如果一个菱形的对角线相等，那么它一定 是正方形 （
√
）
(4)如果一个矩形的对角线互相垂直，那么它 一定是正方形 （ 是正方形（
√
）
(5)四条边相等，且有一个角是直角的四边形
√
）
×
(2)对角线互相垂直且相等的四边形是正方形（
A
D
G B
BE=CF，探索图中AE与BF的关系。
F
E
C
10、如图，点E、F在正方形ABCD的边BC、CD上，
11、如图，在正方形ABCD中，E在BC的延长线上，
且CE=AC，AE交CD于F，则求∠AFC的度数。
A
D
F
B
C
E
12、在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F. 1)试说明:DE=DF 2)只添加一个条件,使四边形EDFA是正方形.
A
G B C
D
F E
A
D G
F
B C E
10、如图，M为正方形ABCD边AB的中 点，E是AB延长线上一点，MN⊥DM， 且交∠CBE的平分线于点N。 （1）求证：MD=MN （2）若将上述条件中的“M是AB的中点” 改为“M为AB上任意一点”，其它条件不 变，问结论MD=MN是否仍然成立。
D F
●
C N M B
D P
●
C N
A
E A
M B
E
11、探究三: 若正方形OEFG继续旋转时AM与
BN之间的关系是否还成立？ 探究四： 如图，有两个大小不等的两个正 方形，其中小正方形的面积是大正方形面 积的一半，若阴影部分的面积为8，则小正 方形的边长为腰直角三角形OAB的两条直 角边AO和BO，使AO=OC，BO=OD 求证：四边形ABCD是正方形。 A O B C D

正方形的性质及判定知识归纳1. 正方形的定义: 有一组邻边相等, 并且有一个角是直角的平行四边形叫做正方形.2. 正方形的性质正方形是特殊的平行四边形、矩形、菱形. 它具有前三者的所有性质: ① 边的性质: 对边平行, 四条边都相等． ② 角的性质: 四个角都是直角.③ 对角线性质：两条对角线互相垂直平分且相等, 每条对角线平分一组对角. ④ 对称性：正方形是中心对称图形, 也是轴对称图形． 平行四边形、矩形、菱形和正方形的关系: （如图） 3. 正方形的判定判定①: 有一组邻边相等的矩形是正方形. 判定②：有一个角是直角的菱形是正方形. 4. 重点：知晓正方形的性质和正方形的判定方法。

难点: 正方形知识的灵活应用例题讲解一、正方形的性质例1: 如图, 已知正方形 的面积为 , 点 在 上, 点 在 的延长线上, 且, 则 的长为FE D CBA变式1: 如图, 在正方形 中, 为 边的中点, , 分别为 , 边上的点, 若 , ,, 则 的长为 .变式2: 将 个边长都为 的正方形按如图所示摆放, 点 分别是正方形的中心, 则 个正方形重叠形成的重叠部分的面积和为例2: 如图, 是正方形 对角线 上的一点, 求证: .EDCBA变式1: 如图, 为正方形 对角线上一点, 于 , 于 .求证: .F EPDCB A例3: 如图, 已知 是正方形 内的一点, 且 为等边三角形, 那么PDCBA变式1: 如图, 已知 、 分别是正方形 的边 、 上的点, 、 分别与对角线 相交于 、 , 若 ,则 .变式2: 如图, 四边形 为正方形, 以 为边向正方形外作正方形 , 与 相交于点 ,则FEDCBA例4: 如图, 正方形 的边 在正方形 的边 上, 连接 , 求证: .GC FEDBA变式1: 如图, 在正方形 中, 为 边上的一点, 为 延长线上的一点, , , 求的度数.BDCAEF变式2: 已知: 如图, 在正方形 中, 是 上一点, 延长 到 , 使 , 连接 并延长交 于 .（1）求证: ；（2）将 绕点顺时针旋转 得到 , 判断四边形 是什么特殊四边形？并说明理由．例5: 若正方形 的边长为 , 为 边上一点, , 为线段 上一点, 射线 交正方形的一边于点 , 且 , 则 的长为 .ABCDEF EG变式1: 如图1, 在正方形 中, 、 、 、 分别为边 、 、 、 上的点, , 连接 、 , 交点为 .⑴ 如图2, 连接 , 试判断四边形 的形状, 并证明你的结论；⑵ 将正方形 沿线段 、 剪开, 再把得到的四个四边形按图3的方式拼接成一个四边形．若正方形 的边长为 , , 则图3中阴影部分的面积为_________ ．图3图1图2H DGC FEBAOH GFEDC BA变式2: 如图, 正方形 对角线相交于点 , 点 、 分别是 、 上的点, , 求证: （1）；（2） . BO D CAQP例6: 如图, 正方形 中, 是 边上两点, 且 于 , 求证:G FEC DBA变式1: 如图, 点 分别在正方形 的边 上, 已知 的周长等于正方形 周长的一半,求 的度数NMDCBA变式2: 如图, 设 正方形 的对角线 , 在 延长线上取一点 , 使 , 与交于 , 求证: 正方形的边长.HEGCDFBA例7: 把正方形 绕着点 , 按顺时针方向旋转得到正方形 , 边 与 交于点 （如图）.试问线段 与线段 相等吗？ 请先观察猜想, 然后再证明你的猜想.GCHF EDB A变式1: 如图所示, 在直角梯形 中, , , 是 的垂直平分线, 交 于点 , 以腰为边作正方形 , 作 于点 , 求证 .lPM FE DC BA二、正方形的判定例1: 四边形 的四个内角的平分线两两相交又形成一个四边形 , 求证: ⑴四边形EFGH 对角互补；⑵若四边形 为平行四边形, 则四边形 为矩形.⑶四边形 为长方形, 则四边形 为正方形．HEFG DCBA变式1: 如图, 已知平行四边形 中, 对角线 、 交于点 , 是 延长线上的点, 且 是等边三角形. ⑴ 求证: 四边形 是菱形；⑵ 若 , 求证：四边形 是正方形．OEDCBA变式2: 已知: 如图, 在 中, , , 垂足为点 , 是 外角 的平分线, , 垂足为点 .⑴ 求证: 四边形 为矩形；⑵ 当 满足什么条件时, 四边形 是一个正方形？并给出证明．M ENCDBA例2: 如图, 是边长为 的正方形, 是内接于 的正方形, , 若 则 =H GFEDCBA例3: 如图, 若在平行四边形 各边上向平行四边形的外侧作正方形, 求证: 以四个正方形中心为顶点组成一个正方形.PRQ S NMFEDCBA1. 附加题:如图, 在线段 上, 和 都是正方形, 面积分别为 和 , 则 的面积为GFEDCB A如图, 在正方形 中, 、 分别是 、 的中点, 求证: .MFEDCBA如图, 正方形 中, 是对角线 的交点, 过点 作 , 分别交 于 , 若 , 则 OFE DC BA如图所示, 是正方形, 为 上的一点, 四边形 恰好是一个菱形, 则 ______.ABCDEF。

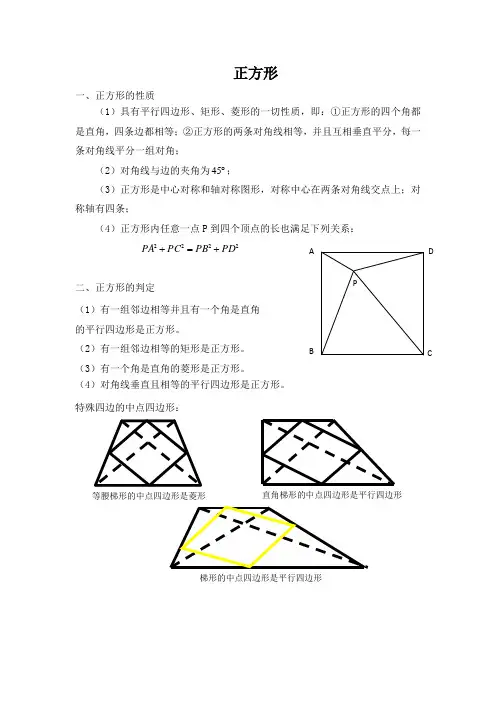
正方形一、正方形的性质（1）具有平行四边形、矩形、菱形的一切性质，即：①正方形的四个角都是直角，四条边都相等；②正方形的两条对角线相等，并且互相垂直平分，每一条对角线平分一组对角；（2）对角线与边的夹角为︒45；（3）正方形是中心对称和轴对称图形，对称中心在两条对角线交点上；对称轴有四条；（4）正方形内任意一点P 到四个顶点的长也满足下列关系： 2222PD PB PC PA +=+二、正方形的判定（1）有一组邻边相等并且有一个角是直角 的平行四边形是正方形。

（2）有一组邻边相等的矩形是正方形。

（3）有一个角是直角的菱形是正方形。

（4）对角线垂直且相等的平行四边形是正方形。

特殊四边的中点四边形：ABCDP等腰梯形的中点四边形是菱形直角梯形的中点四边形是平行四边形梯形的中点四边形是平行四边形平行四边形的中点四边形是平行四边形矩形的中点四边形是菱形菱形的中点四边形是矩形正方形的中点四边形是正方形归纳：特殊四边形的中点四边形：◆平行四边形的中点四边形是平行四边形◆矩形的中点四边形是菱形◆菱形的中点四边形是矩形◆正方形的中点四边形是正方形◆等腰梯形的中点四边形是菱形◆直角梯形的中点四边形是平行四边形◆梯形的中点四边形是平行四边形一般四边形的中点四边形：决定中点四边形EFGH的形状的主要因素是原四边形ABCD的对角线的长度和位置关系例题分析例1 下列叙述错误的是（）A.既是矩形又是菱形的四边形是正方形B.有一组邻边相等的矩形是正方形C.有一个角是直角的菱形是正方形D.对角线相等且互相垂直的四边形是正方形例2 如图1-3-1，正方形ABCD 的面积为256，点E 在AD 上，点F 在AB 的延长线上，EC ⊥FC ，∆CEF 的面积是200，则BF 的长是 .例 3 已知E 为边长是1的正方形ABCD 内一点，且AEB S ∆=0.1999，则CED S ∆= .例4 如图1-3-2，正方形ABCD 的边长AB=20，F 为AD 上的一点，连接CF ，作CE ⊥CF 交AB 的延长线于E ，作DG ⊥CF 交CF 于G ，若BE=15，则DG 的长为 .例5 如图1-3-3，正方形ABCD 中，E ，F 为BC ，CD 上的点，且∠EAF=45°，求证EF=BE+DF .1-3-11-3-21-3-3例6 如图1-3-4，正方形ABCD 的边长为4，E ，F 分别为AD ，BC 上的两个点，且BF=DE=1，从EF 的中点O 作EF 的垂直平分线，交CD 于G ，则OG = .例7 如图1-3-5，正方形ABCD 的边长为a ，E ，F ，G ，H 分别在正方形的四条边上，已知EF//GH ，EF=GH ，（1）若AE=AH=13a ，求四边形EFGH 的周长和面积；（2）求四边形EFGH 的周长的最小值.例8 如图1-3-6，已知E 是正方形ABCD 内一点，且∠ECD=∠EDC=15°，则AEB ∠= .90.DEC D DE A DE A AD AEB ∆︒''∆∆∠分析：利用旋转将以为中心顺时针旋转得到，再将以为轴对称即可得出度数1-3-41-3-61-3-51-3-81.在正方形ABCD 内有点P ，使∆PAB 、 ∆PBC 、∆PCD 、∆PDA 都是等腰三角形，那么具有这样性质的点是 个2.已知边长为4的正方形ABCD 中，F 是AD 的中点，E 点在AB 边上，且AE:EB=1:3，那么EFC S ∆= .3.一张边长为6的长方形纸片，按图1-3-7加以折叠，使得一角顶点落在对边上，则折痕长为 .4.若P 是边长为1的正方形ABCD 内一点，且0.31ABP S ∆=，则DCP S ∆= .5.边长为10的正方形，把边长增加同样的长度后，所得面积是625，则边长增加了 .6.如图1-3-8将正方形内接于等腰Rt ABC ∆，如果按照图甲的放法，可求得该正方形的面积是441，如果按照图乙的放法，那么只能放边长为 的正方形1-3-77.如图1-3-9，在面积为1的正方形ABCD 内取一点P ，使PBC ∆为等边三角形，求∆BPD 的面积.8.如图1-3-10，正方形OPQR 内接于∆ABC .已知∆AOR 、∆BOP 和∆CRQ 的面积分别是1、3和1.试求正方形OPQR 的面积.9.如图1-3-11，已知正方形AC 、BD 相交于点O ，BE 平分∠OBA ，CF ⊥BE 与F ，交OB 于G ，求证OE=OG.10.如图1-3-12，点P 在正方形ABCD 内，若PA:PB:PC=1：2：3，求∠APB 的度数.1-3-91-3-101-3-111-3-1211.如图1-3-13，过正方形ABCD 的顶点B 作直线l ，过,A C 作l 的垂线，垂足分别为,E F .若1AE =，3CF =，则AB 的长度为 .练习12（中，折叠与正方形的性质）如图1-3-14，在正方形纸片ABCD 中，对角线AC 、BD 交于点O ，折叠正方形纸片ABCD ，使AD 落在BD 上，点A 恰好与BD 上的点F 重合。

正⽅形的性质与判定专题练习正⽅形专题训练（含答案）A.相等的⾓⼀定是对顶⾓.选择题（共11⼩题）1.如图，将正⽅形OABC放在平⾯直⾓坐标系中, B.四个⾓都相等的四边形⼀定是正⽅形C.平⾏四边形的对⾓线互相平分原点，A的坐标为（1,嶺），则点C的坐标为（D .矩形的对⾓线⼀定垂直5-2 .）如图，点3E在正⽅形/ ;⼫ABCD的对⾓O1⼥线AC上，且EC=2AE，直⾓三⾓形FEG的两直⾓边EF、EG分别交BC、DC于点M、N .若正⽅形ABCD 的边长为a,则重叠部分四边形EMCN的⾯积为（C.3 .如图，F是正⽅形ABCD的边CD上的⼀个动点，BF的垂直平分线交对⾓线AC于点E,连接BE,FE,则/ EBF的度数是（)OB. 50A .45 °4.平⾏四边形、矩形、菱形、正⽅形都具有的是（A.对⾓线互相平分对⾓线互相垂直C.对⾓线相等5.正⽅形的⼀条对⾓线长为则这个正⽅形的⾯积是()A. 86.（2014?福州）如图，在正⽅形C .60 °D. 757. 顺次连接菱形各边的中点所形成的四边形是（等腰梯形B.矩形C.菱形D.正⽅形8. F列说法中，正确的是（9 .已知四边形ABCD是平⾏四边形，再从①AB=BC ,②/ ABC=90 ° ③AC=BD ,④AC丄BD四个条件中,选两个作为补充条件后，使得四边形ABCD是正⽅形,现有下列四种选法，其中错误的是（A .选①②B .选②③10.如图，在正⽅形ABCD那么/ ANM等于（11.如图，菱形ABCD为边长的正⽅形ACEFB. 16C .选①③D .选②④中，CE=MN , / MCE=35 °中,C .55°/ B=60的⾯积为（C. 2060°,AB=5 ,则以AC25⼆.填空题（共5⼩题）12.如图，在正⽅形ABCD的外侧, 作等边三⾓形ADE ,对⾓线互相垂直且相等E13.如图，已知P是正⽅形ABCD对⾓线BD上⼀点,且BP=BC，贝U / ACP度数是度.14.如图，四边形ABCD为正⽅形，△ ADE为等边三⾓形.AC为正⽅形ABCD的对⾓线，则/ EAC=度.15.已知：如图，菱形ABCD 中，/ B=60 ° AB=4，则以AC为边长的正⽅形ACEF的周长为20.在平⾯内正⽅形ABCD与正⽅形CEFH如图放置,16?如图所⽰，正⽅形ABCD的周长为16cm,顺次连接正⽅形ABCD各边的中点，得到四边形EFGH，则四边形EFGH的周长等于cm,四边形EFGH的⾯积等于cm.￡__⼝三.解答题（共6⼩题）17.如图，正⽅形ABCD 中, E、F分别为BC、CD上的点，且AE丄BF，垂⾜为点G.求证：AE=BF .18.如图，在正⽅形ABCD中，P是对⾓线AC上的⼀点, 连接BP、DP,延长BC⾄U E，使PB=PE .求证: 连DE，BH，两线交于M .求证：（1）BH=DE .(2) BH 丄DE .21.已知：如图，？ABCD中，0是CD的中点，连接AO并延长，交BC的延长线于点E . （1）求证:△ AOD ◎△ EOC ; (2)连接AC , DE，当/ B= / AEB= _ 。

八年级数学下册考点知识与题型专题讲解与提升练习专题41 根据正方形的性质与判定求角度一、单选题1．如图，在正方体的两个面上画了两条对角线AB 、AC ，则BAC ∠等于（）A ．135°B ．90°C ．75°D ．60°2．如图，点E 为正方形ABCD 内一点，AD ED =，70AED ∠=︒，连结EC ，那么AEC ∠的度数是( )A ．105︒B ．130︒C ．135︒D ．140︒3．如图，正方形ABCD 中，点E 、F 分别是BC 、CD 上的点，且CE=CF ，点P 、Q 分别是AF 、EF 的中点，连接PD 、PQ 、DQ ，则△PQD 的形状是（ ）A．等腰三角形B．直角三角形C．等腰非直角三角形D．等腰直角三角形4．如图，在正方形ABCD中，以对角线BD为边作菱形BDFE，连接BF，则∠AFB＝（）A．22.5°B．25°C．30°D．不能确定5．（2013台州）如图，四边形ABCD、AEFG均为正方形，其中E在BC上，且B、E两点不重合，并连接BG．根据图中标示的角判断下列∠1、∠2、∠3、∠4的大小关系正确的是（）A．∠1＜∠2B．∠1＞∠2C．∠3＜∠4D ．∠3＞∠46．如图，在菱形ABCD 中，AB=AC=1，点E 、F 分别为边AB 、BC 上的点，且AE=BF ，连接CE 、AF 交于点H ，连接DH 交AC 于点O ，则下列结论：①△ABF≌△CAE；②∠FHC=∠B；③△ADO≌△ACH；④ABCD S 菱形；其中正确的结论个数是（）A ．1个B ．2个C ．3个D ．4个7．如图，正方形ABCD 中，点E 是AD 边的中点，BD 、CE 交于点H ，BE 、AH 交于点G ，则；③S △BHE =S △CHD ；④∠AHB=∠EHD．其中正确的个数是A ．1B ．2C ．3D ．48．如图，点P 是正方形ABCD 的对角线BD 上一点(点P 不与点B 、D 重合)，PE⊥BC 于点E ，PF⊥CD 于点F ，连接EF 给出下列五个结论：①AP＝EF ；②AP⊥EF；③仅有当∠DAP＝45°或67.5°时，△APD 是等腰三角形；④∠PFE＝∠BAP：⑤2PD ＝EC ．其中有正确有()个．A ．2B ．3C ．4D ．59．如图，正方形ABCD 中，点E 、F 分别在BC 、CD 上，△AEF 是等边三角形连接AC 交EF 于G ，下列结论: ①BE＝DF ，②∠DAF＝15°，③AC⊥EF，④BE+DF＝EF ，⑤EC＝FG ；其中正确结论有( )个A ．2B ．3C ．4D ．5二、填空题 10．如图，点E 在正方形ABCD 的边BA 的延长线上，连接AC ，AC ＝AE ，CE 交AD 于点F ，则∠ACE 的度数等于_____．11．如图，正方形ABCD 中，E 为CD 边上一点，F 为BC 延长线上一点，且CE CF =，若19EFD ∠=︒，则BEC ∠=____________︒．12．如图，点P 是正方形ABCD 内的一点，且PA=1，，则∠APB 的度数为_______．13．如图，P 是正方形ABCD 内一点，且PA ＝PD ，PB ＝PC ．若∠PBC ＝60°，则∠PAD ＝_____．14．如图，在正方形ABCD 中，以BC 为边在正方形外部作等边三角形BCE ，连结DE,则∠CDE 的度数为______°.15．如图，四边形ABCD 中AD AB =， 90DAB BCD ∠=∠=︒．则ACB =∠______．16．如图，正方形OABC 的面积为50，对角线OB 在直线2y x =上，则点C 的坐标是_________.17．如图，点E为正方形ABCD边CB延长线上一点，点F为AB上一点，连接AE，CF，AC，若BE=BF，∠E=70°，则∠ACF=_____．18．如图，正方形ABCD中，点E在BC的延长线上，AE平分∠DAC，则下列结论：（1）∠E＝22.5°；（2）∠AFC＝112.5°；（3）∠ACE＝135°；（4）AC＝CE；（5）AD：CE＝1_____（填写序号）19．如图，在矩形ABCD中，∠DAC=65°，点E是CD上一点，BE交AC于点F，将△BCE 沿BE折叠，点C恰好落在AB边上的点C′处，则∠AFC′=_______．20．如图，P为正方形ABCD内一点，PA：PB：PC=1：2：3，则∠APB=_____________ .21．如图，在正方形ABCD 中，边长为2的等边三角形AEF 的顶点E 、F 分别在BC 和CD上，下列结论：①CE=CF；②∠AEB=75°；③BE+DF=EF；④S 正方形ABCD =2．其中正确的序号是_____（把你认为正确的都填上）．22．如图，在Rt ABC 中，90ABC ∠=︒，3cm AB =，4cm BC =，AD 和CD 分别是其外角CAG ∠和ACF ∠的角平分线，延长DA 和CB 相交于点E ，则D ∠=_____度，BE =_____cm ．三、解答题23．如图是由边长为 1 的 10×14 的正方形构成的网格，每个小正方形的顶点叫做格点．（1）如图 1，△ ABC 的顶点在格点上，完成下列问题：①用无刻度直尺画出在格点上点 D ，使 CD⊥AC 且 CD=AC ；②直接写出△ ACD 的面积是，AC 长；（2）如图 2，△ MNP 的顶点在格点上，用无刻度直尺画出在射线 MP 上的格点 Q，使∠PNQ=45°．24．如图，菱形ABCD的对角线AC、BD相交于点O，分别延长OA，OC到点E，F，使AE ＝CF，依次连接B，F，D，E各点．（1）求证：四边形BFDE为菱形；（2）若∠ABC＝60°，则当∠EBA＝°时，四边形BFDE是正方形．25．如图，在正方形ABCD中，E是边AB上的任意一点(不与点A，B重合)，连接DE，作点A关于直线DE的对称点为F，连接EF并延长交BC于点G．（1）依题意补全图形，连接DG，求∠EDG的度数；（2）过点E作EH⊥DE交DG的延长线于点H，连接BH．线段BH与AE有怎样的数量关系，请写出结论并证明．26．综合与实践问题情境：如图1，在正方形ABCD中，点E是对角线AC上的一点，点F在BC的延长线上，且BE EF=，EF交CD于点G．问题解决：（1）求证：DE EF=；（2）求DEF∠的度数；探索发现：（3）如图2，若点F在边BC上，且BE EF∠的度数．=，求DEF27．如图，E、F是正方形ABCD的边AD上的两个动点，满足AE=DF．连接CF交BD于G，连接BE交AG于H．已知正方形ABCD的边长为4cm，解决下列问题：（1）求证：BE⊥AG；（2）求线段DH的长度的最小值．28．如图，△ABC 中，点O 是边AC 上一个动点，过O 作直线MN∥BC，设MN 交∠ACB 的平分线于点E，交∠ACB 的外角平分线于点F．（1）求证：OE＝OF；（2）当点O 在边AC 上运动到什么位置时，四边形AECF 是矩形？并说明理由．（3）若AC 边上存在点O，使四边形AECF 是正方形，猜想△ABC 的形状并证明你的结论．29．如图，在正方形ABCD中，点P是AD边上的一个动点，连接PB，过点B作一条射线与边DC的延长线交于点Q，使得∠QBE＝∠PBC，其中E是边AB延长线上的点，连接PQ．(1)求证：△PBQ是等腰直角三角形；(2)若PQ2＝PB2+PD2+1，求△PAB的面积．30．如图，在正方形ABCD纸片上有一点P，PA=1，PD=2，PC=3，现将△PCD剪下，并将它拼到如图所示位置（C与A重合，P与G重合，D与D重合），求∠APD的度数．31．如图1，点O为正方形ABCD 的中心，E为AB 边上一点，F为BC边上一点，△EBF 的周长等于BC 的长.（1）求∠EOF 的度数.（2）连接OA、OC（如图2）.求证：△AOE∽△CFO.（3）若OF，求AECF的值.32．如图，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，过点A作AG⊥EB，垂足为G，AG交BD于F，则OE=OF．（1）请证明OE=OF（2）解答（1）题后，某同学产生了如下猜测：对上述命题，若点E在AC的延长线上，AG⊥EB，AG交 EB的延长线于 G，AG的延长线交DB的延长线于点F，其他条件不变，则仍有OE=OF．问：猜测所得结论是否成立？若成立，请给出证明；若不成立，请说明理由．33．如图1，在正方形ABCD中，P是对角线BD上的点，点E在AB上，且PA=PE．（1）求证：PC=PE；（2）求∠CPE的度数；（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，试探究∠CPE与∠ABC之间的数量关系，并说明理由．34．如图①，在平面直角坐标系中，AB⊥x轴于B，AC⊥y轴于C，点C(0，m)，A(n，m)，且(m－4)2＋n2－8n＝－16，过C点作∠ECF分别交线段AB，OB于E，F两点．(1)求A点的坐标；(2)若OF＋BE＝AB，求证：CF＝CE；(3)如图②，若∠ECF＝45°，给出两个结论：①OF＋AE－EF的值不变；②OF＋AE＋EF的值不变，其中有且只有一个结论正确，请你判断出正确的结论，并加以证明和求出其值．⊥，且35．已知正方形ABCD，P为边AB上一点(P不与A、B重合），过P作PE CP =，连接AE．CP PE（1）如图1，求EAD∠的度数；（2）如图2，连接CE交BD于G，求证：+=；AE DG2（3）如图2，当10BC =，6PA =，则BG =（直接写出结果）36．阅读下面的例题及点拨，补全解题过程（完成点拨部分的填空），并解决问题： 例题：如图1，在等边ABC 中，M 是BC 边上一点（不含端点,B C ），N 是ABC 的外角ACH ∠的平分线上一点，且AM MN =.求证：60AMN ∠=︒．点拨：如图2，作60CBE ∠=︒，BE 与NC 的延长线相交于点E ，得等边BEC △，连结EM ，易证ABM EBM △≌△（_______），可得AM EM =，12∠=∠；又AM MN =，则EM MN =，可得∠____=∠_____；由314560∠+∠=∠+∠=︒，进一步可得12∠=∠=∠______；又因为26120∠+∠=︒，所以56120∠+∠=︒，所以60AMN ∠=︒．问题：如图3，四边形ABCD 的四条边都相等，四个角都等于90︒，M 是BC 边上一点（不含端点,B C ），N 是四边形ABCD 的外角DCH ∠的平分线上一点，且AM MN =．求AMN ∠的度数．37．如图，BF 平行于正方形ABCD 的对角线AC ，点E 在BF 上，且AE AC =，CF AE ，求BCF ∠的度数.38．如图1，有一组平行线l1∥l2∥l3∥l4，正方形ABCD的四个顶点分别在l1，l2，l3，l 4上，EG过点D且垂直l1于点E，分别交l2，l4于点F，G，EF=DG=1，DF=2．（1）AE=__________，正方形ABCD的边长=__________；（2）如图2，将∠AEG绕点A顺时针旋转得到∠AE′D′，旋转角为α（0°＜α＜90°），点D′在直线l3上，以AD′为边在E′D′左侧作菱形AB′C′D′，使B′、C′分别在直线l2，l4上．①写出∠B′AD′与α的数量关系并给出证明；②若α=30°，直接写出菱形AB′C′D′的边长为__________．。

1.3正方形的性质与判定新思维同步提高训练（Word版含解答）-2021-2022学年九年级数学北师大版上册一、选择题1.如图，将正方形OEFG放在平面直角坐标系中，O是坐标原点，点E(2,3)，则点F的坐标为（）A. (−1,5)B. (−2,3)C. (5,−1)D. (−3,2)2.如图，在正方形ABCD中，AB＝3，点E，F分别在边AB，CD上，∠EFD＝60°．若将四边形EBCF 沿EF折叠，点B恰好落在AD边上，则BE的长度为（）A. 1B. √2C. √3D. 23.如图，在边长为2的正方形ABCD中，连接对角线AC，将△ADC沿射线CA的方向平移得到△A′D′C′，分别连接BC′，AD′，BD′，则BC′+BD′的最小值为（）A. 2√2B. 4C. 4√2D. 2√54.如图，在正方形ABCD中，AB=6，点Q是AB边上的一个动点（点Q不与点B重合），点M，N分别是DQ，BQ的中点，则线段MN=（）5.如图，在△ABC中，∠ACB＝90°，以△ABC的各边为边作三个正方形，点G落在HI上，若AC＋BC＝6，空白部分面积为10.5，则AB的长为（）A. 3 √2B. √19C. 2 √5D. √266.如图，在正方形ABCD中，E为DC边上的一点，沿线段BE对折后，若∠ABF比∠EBF大15°，则∠EBF的度数为（）A. 15°B. 20°C. 25°D. 30°7.如图，△ABE、△BCF、△CDG、△DAH是四个全等的直角三角形，其中，AE＝5，AB＝13，则EG的长是（）A. 7 √2B. 6 √2C. 7D. 7 √38.如图，在△ABC中，∠ACB=90°，以△ABC的各边为边分别作正方形BAHI，正方形BCFG与正方形CADE.延长BG，FG分别交AD，DE于点K，J，连结DH，IJ.图中两块阴影部分面积分别记为S1，S2，若S1:S2=1:4，四边形S BAHE=18，则四边形MBNJ的面积为（）A. 5B. 6C. 8D. 99.由四个全等的直角三角形和一个小正方形组成的大正方形 ABCD 如图所示.过点 D 作 DF 的垂线交小正方形对角线 EF 的延长线于点 G ，连结 CG ，延长 BE 交 CG 于点 H .若 AE =2BE ，则CG BH 的值为（ ）A. 32B. √2C. 3√107D. 3√55 10.如图，正方形 ABCD 中，在 AD 的延长线上取点 E ， F ，使 DE =AD ， DF =BD ，连接 BF 分别交 CD ， CE 于 H ， G ，下列结论：① HF =2HG ；② ∠GDH =∠GHD ；③图中有8个等腰三角形；④ S △CDG =S △DNF ．其中正确的结论个数是（ ）A. 1个B. 2个C. 3个D. 4个二、填空题11.如图，若该正方形ABCD 边长为10，将正方形沿着直线MN 翻折，使得BC 的对应边 B ′C ′ 恰好经过点A ， 过点A 作 AG ⊥MN ，垂足分别为G ， 若 AG =6 ，则 AC ′ 的长度为________．12.已知直角三角形ABC ，∠ABC=90°，AB=3，BC=5，以AC 为边向外作正方形ACEF ，则这个正方形的中心O 到点B 的距离为________．13.如图，矩形纸片ABCD，AD=2AB=4，点F在线段AD上，将△ABF沿BF向下翻折，点A的对应点E 落在线段BC上，点M，N分别是线段AD与线段BC上的点，将四边形CDMN沿MN向上翻折，点C 恰好落在线段BF的中点C'处，则线段MN的长为________．14.如图，在平面直角坐标系中有一边长为1的正方形OABC，边OA、OC分别在x轴、y轴上，如果以对角线OB为边作第二个正方形OBB1C1，再以对角线OB1为边作第三个正方形OB1B2C2，照此规律作下去，则点B2020的纵坐标为________15.如图1是公园某处的几何造型，如图2是它的示意图，正方形的一部分在水平面EF下方，测得DE=2米，∠CDF=45°，露出水平面部分的材料长共合计140米（注：共8个大小一样的正方形造型，不计损耗），点B到水平面EF的距离为________米.16.如图，正方形ABCD中，AB=4，O是BC边的中点，点E是正方形内一动点，OE=2，连接DE，将线段DE绕点D逆时针旋转90°得DF，连接AE、CF.则线段OF长的最小值为________.三、解答题17.在正方形ABCD中，E是CD边上一点（CE>DE），AE，BD交于点F．（1）如图1，过点F作GH⊥AE，分别交边AD，BC于点G，H．求证：∠EAB=∠GHC；（2）AE的垂直平分线分别与AD，AE，BD交于点P，M，N，连接CN．①依题意补全图形；图1 备用图②用等式表示线段AE与CN之间的数量关系，并证明．18.问题情境：（1）如图1，已知正方形ABCD，点E在CD的延长线上，以CE为边构造正方形CEFG，连接BE和DG，则BE和DG的关系为________。

正方形的性质及判定练习题一、知识梳理：1、定义：一组邻边相等的矩形是正方形．2、正方形性质：（1）边的性质：对边平行，四条边都相等．（2）角的性质：四个角都是直角．（3）对角线的性质：两条对角线互相垂直平分且相等，•每条对角线平分一组对角．（4）对称性：既是轴对称图形，又是中心对称图形．3、判定：（1）一组邻边相等的矩形是正方形（2）对角线互相垂直的矩形是正方形（3）有一个是直角的菱形是正方形（4）对角线相等的菱形是正方形总结：矩形+（或）=正方形菱形+（或）=正方形二、基础训练：性质：1、如图，四边形ABCD是正方形，两条对角线相交于点O．（1）一条对角线把它分成_______个全等的________ 三角形；（2）两条对角线把它分成_______个全等的________三角形；图中一共有________个等腰直角三角形；（3）∠AOB＝_____度，∠OAB＝_____度．（4）AB: AO: AC=________．2、正方形具有而矩形不一定具有的性质是( )A、四个角相等B、对角线互相垂直平分C、对角互补D、对角线相等.3、正方形具有而菱形不一定具有的性质（）A、四条边相等.B、对角线互相垂直平分C、对角线平分一组对角D、对角线相等.4、正方形对角线长6，则它的面积为_________ ,周长为________．5、如图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中四边形ABCD和EFGH都是正方形．求证：△ABF≌△DAE．判定：F A B C D 1. 下列说法错误的是（ ）Ａ．两条对角线相等的菱形是正方形 Ｂ．两条对角线相等且垂直平分的四边形是正方形Ｃ．两条对角线垂直且相等的四边形是正方形 Ｄ． 两条对角线垂直的矩形是正方形2．四个内角都相等的四边形一定是（ ）A ．正方形B ．菱形C ．矩形D ．平行四边形3.已知在□ABCD 中，∠A=90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是（ ）A ．∠D=90° B.AB=CD C. AD=BC D. BC=CD4.四边形ABCD 中，AC 、BD 相交于点O ，能判别这个四边形是正方形的条件是（ ）A. OA=OB=OC=OD ，AC ⊥BDB. AB ∥CD ，AC=BDC. AD ∥BC ，∠A=∠CD. OA=OC ，OB=OD ，AB=BC5.能使平行四边形ABCD 为正方形的两个条件是 ________ _________ ___________________________________________________________ ．（最少填三组）三、【聚焦“中考”】例：如图，在△ABC 中，AB=AC ，D 是BC 的中点，DE ⊥AB ，DF ⊥AC ，垂足分别为E 、F ． （1）求证：DE=DF ．（2）只添加一个条件，使四边形EDFA 是正方形，•请你至少写出两种不同的添加方法．（不另外添加辅助线，无需证明）自我检测：1.如图，在ABC 中∠ACB=90°，CD 平分∠ACB，DE ⊥BC ，DF⊥AC,垂足分别为E 、F ， 求证：四边形CFDE 为正方形2. 如图所示，在Rt ΔABC 中，∠C ＝90°，∠A 、∠B 的平分线交于点D ，DE ⊥BC 于E ，DF ⊥AC 于F ，试说明四边形CEDF 为正方形。

北师大版数学九年级上册第一章第三节正方形的性质与判定课时练习一、单选题（共15题）1.菱形，矩形，正方形都具有的性质是（）A．对角线相等且互相平分B．对角线相等且互相垂直平分C．对角线互相平分D．四条边相等，四个角相等答案：C解析：解答：解：A.不正确，菱形的对角线不相等；B.不正确，菱形的对角线不相等，矩形的对角线不垂直；C.正确，三者均具有此性质；D.不正确，矩形的四边不相等，菱形的四个角不相等；故选C．分析:对菱形对角线相互垂直平分，矩形对角线平分相等，正方形对角线相互垂直平分相等的性质进行分析从而得到其共有的性质2.如图，在正方形ABCD中，E、F分别是边CD、AD上的点，且CE=DF．AE与BF相交于点O，则下列结论错误的是（）A．AE=BF B．AE⊥BFC．AO=OE D．S△AOB=S四边形DEOF答案：C解析：解答: A.∵在正方形ABCD中，∴AB=BC=CD=AD，又∵CE=DF，∴AF=DE，∵∠D=∠BAF=90°，∴△BAF≌△ADE，∴AE=BF，故此选项正确；B.∵△BAF≌△ADE，∴∠BFA=∠AED，∵∠AED+∠EAD=90°，∴∠BFA+∠EAD=90°，∴∠AOF=90°，∴AE⊥BF，故此选项正确；C.连接BE，假设AO=OE，∵BF⊥AE，∴∠AOB=∠BOE=90°，∵BO=BO，∴△ABO≌△EBO，∴AB=BE，又∵AB=BC，BC＜BE，∴AB不可能等于BE，∴假设AO=OE，不成立，即AO≠OE，故此选项错误；D.∵△BAF≌△ADE，∴S△BAF=S△ADE，∴S△BAF -S△AOF=S△ADE-S△AOF，∴S△AOB=S四边形DEOF，故此选项正确．故选C．分析: 首先利用全等三角形的判定方法利用SAS证明△BAF≌△ADE，即可得出AE=BF，进而得出∠BFA+∠EAD=90°，即AE⊥BF，用反证法证明AO≠EO，利用三角形全等即面积相等，都减去公共面积剩余部分仍然相等，即可得出D正确3.正方形具有而菱形不一定具有的性质是（）A．四条边相等B．对角线互相垂直平分C．对角线平分一组对角D．对角线相等答案：D解析：解答: 正方形的性质：正方形的四条边相等，四个角都是直角，对角线互相垂直平分且相等，并且每一条对角线平分一组对角；菱形的性质：菱形的四条边相等，对角线互相垂直平分，并且每一条对角线平分一组对角；因此正方形具有而菱形不一定具有的性质是：对角线相等；故选：D．分析: 根据正方形和菱形的性质容易得出结论4.如图，正方形ABCD的对角线BD长为22，若直线l满足：（1）点D到直线l的距离为1，（2）A、C两点到直线l的距离相等，则符合题意的直线l的条数为（）A．1 B．2 C．3 D．4答案:D解析：解答:连接AC与BD相交于O，∵正方形ABCD的对角线BD长为22∴OD=2∴直线l∥AC并且到D的距离为1，同理，在点D的另一侧还有直线满足条件，故共有4条直线l．故选：D．分析: 连接AC与BD相交于O，根据正方形的性质求出OD=2，然后根据点到直线的距离和平行线间的距离相等解答5.若正方形的周长为40，则其对角线长为（）A．100 B．202C．102D．10答案:C解析：解答: ∵正方形的周长为40，∴正方形的边长为10，∴对角线长为102故选C．分析: 根据正方形的周长，可将正方形的边长求出，进而可将正方形对角线的长求出．6.已知在正方形ABCD中，对角线AC与BD相交于点O，OE∥AB交BC于点E，若AD=8cm，则OE的长为（）A．3cm B．4cm C．6cm D．8cm答案:B解析：解答: ∵四边形ABCD是正方形，∴AD=AB=8cm，OA=OC，∵OE∥AB，∴OE是△ABC的中位线，∴OE=12AB=4cm，故选B．分析:根据正方形的性质得出AD=AB=8，AO=OC，由OE∥AB，得出OE是△ABC的中位线解答即可7. 如图，点E在正方形ABCD的边AD上，已知AE=7，CE=13，则阴影部分的面积是（）A．114 B．124 C．134 D．144答案:A解析：解答：∵四边形ABCD是正方形，∴∠D=90°，AB=BC=AD，设AB=BC=AD=x，则DE=x-7，∵CD2+DE2=CE2，∴x2+（x-7）2=132，解得：x=12，或x=-5（不合题意，舍去），∴BC=AB=12，∴阴影部分的面积=12（AE+BC）•AB=12×（7+12）×12=114；故选：A．分析: 本题考查了正方形的性质、勾股定理、以及梯形面积的计算；熟练掌握正方形的性质，并能进行推理计算是解决问题的关键8.如图，已知点E为正方形ABCD对角线BD上一点，且BE=BC，则∠DCE的度数为（）A．30°B．22.5°C．15°D．45°答案:B解析：解答: ∵正方形ABCD，∴BC=CD，∠DBC=∠BDC=45°，∵BE=BC，∴∠BEC=∠BCE=67.5°，∴∠DCE=∠BCD-∠BCE=90°-67.5°=22.5°，故选B．分析: 由正方形的性质得到BC=CD，∠DBC=∠BDC=45°，根据BE=BC，根据三角形的内角和定理求出∠BEC=∠BCE=67.5°，根据∠DCE=∠BCD-∠BCE即可求出答案．9.如图，在正方形ABCD的外侧，作等边三角形ADE，连结BE交AD于点F，则∠DFE的度数为（）A．45°B．55°C．60°D．75°答案:D解析：解答: ∵四边形ABCD是正方形，∴AB=AD，∠BAS=90°，∵△AED是等边三角形，∴∠AED=∠EAD=60°，AE=AD，∴∠BAE=150°，AB=AE，∴∠ABE=∠AEB=12（180°-150°）=15°，∴∠DFE=∠AFB=90°-15°=75°，故选D．分析: 根据正方形的性质得出AB=AD，∠BAS=90°，根据等边三角形的性质得出∠AED=∠EAD=60°，AE=AD，求出∠BAE=150°，AB=AE，∠ABE=∠AEB=15°，求出∠AFB即可10.在正方形ABCD所在平面内找一点P，使P点与A、B、C、D中两点都连在一个等边三角形，那么这样的P点有（）A．5个B．12个C．9个D．15个答案:B解析：解答: 在四条边垂直平分线上的点，与相邻的两个点连成一个等边三角形，共有8个点；在两条对角线上的点，与相对的两个点连成一个等边三角形，共有4个点；共有8+4=12个点满足条件．故选：B．分析: 在四条边垂直平分线上，每一条可以找到两个点，与相邻的两个点连成一个等边三角形，共有8个点；在两条对角线上，每一条可以找出2个点，与相对的两个点连成一个等边三角形，共有4个点；由此得出共有8+4=12个点满足条件11.如图，正方形ABCD的三边中点E、F、G．连ED交AF于M，GC交DE于N，下列结论：①GM⊥CM；②CD=CM；③四边形MFCG为等腰梯形；④∠CMD=∠AGM．其中正确的有（）A．①②③B．①②④C．①③④D．①②③④答案:A解析：解答: ∵由已知，AG∥FC且AG=FC，故四边形AGCF为平行四边形，∴∠GAF=∠FCG又AE=BF，AD=AB，且∠DAE=∠ABF，可知∠ADE=∠BAF∴DE⊥AF，DE⊥CG．又∵G点为中点，∴GN为△ADM的中位线，即CG为DM的垂直平分线，可证CD=CM，∴∠CDG=∠CMG，即GM⊥CM．又∠MGN=∠DGC=∠DAF（外角等于内对角），∴∠FCG=∠MGC．故选A．分析:要证以上问题，需证CN是DN是垂直平分线，即证N点是DM中点，利用中位线定理即可12.如图，在正方形ABCD中，点E、F分别在CD、BC上，且BF=CE，连结BE、AF相交于点G，则下列结论：①BE=AF；②∠DAF=∠BEC；③∠AFB+∠BEC=90°；④AF⊥BE 中正确的有（）A．①②③B．②③④C．①②③④D．①②④答案:D解析：解答: ∵四边形ABCD是正方形，∴∠ABF=∠C=90°，AB=BC，∵BF=CE，∴△ABF≌△BCE．∴AF=BE．（①正确）∠BAF=∠CBE，∠BFA=∠BEC，（③错误）∵∠BAF+∠DAF=90°，∠BAF+∠BFA=90°，∴∠DAF=∠BEC．（②正确）∵∠BAF=∠CBE，∠BAF+∠AFB=90°，∴∠CBE+∠AFB=90°，∴AF⊥BE．（④正确）所以正确的是①②④．故选D．分析:分析图形，根据正方形及三角形性质找到各角边的关系就很容易求解13.如图，正方形ABCD的对角线BD长为22，若直线l满足：①点D到直线l的距离为3②A、C两点到直线l的距离相等．则符合题意的直线l的条数为（）A．1 B．2 C．3 D．4答案:B解析：如图，连接AC与BD相交于O，∵正方形ABCD的对角线BD长为22∴OD=2∴直线l∥AC并且到D的距离为3同理，在点D的另一侧还有一条直线满足条件，故共有2条直线l．故选：B．分析: 连接AC与BD相交于O，根据正方形的性质求出OD=2，然后根据点到直线的距离和平行线间的距离相等解答．14.平行四边形、矩形、菱形、正方形都具有的是（）A．对角线互相平分B．对角线互相垂直C．对角线相等D．对角线互相垂直且相等答案:A解析：解答：A.对角线相等是平行四边形、矩形、菱形、正方形都具有的性质；B.对角线互相垂直是菱形、正方形具有的性质；C.对角线相等是矩形和正方形具有的性质；D.对角线互相垂直且相等是正方形具有的性质．故选：A．分析:本题主要依据平行四边形、矩形、菱形、正方形都具有对角线相互平分的性质来判断15.如图，正方形ABCD中，AE=AB，直线DE交BC于点F，则∠BEF=（）A．35°B．45°C．55°D．60°答案:B解析：解答：∵四边形ABCD是正方形，∴AB=AD，∠BAD=90°，∵AE=AB，∴AE=AB=AD，∴∠ABE=∠AEB，∠AED=∠ADE，∠ABE+∠AEB+∠BAE=180°，∠AED+∠ADE+∠DAE=180°，∵∠BAE+∠DAE=∠BAD=90°，∴∠ABE+∠AEB+∠AED+∠ADE=270°，∴∠AEB+∠AED=135°，即∠BED=135°，∴∠BEF=180°-135°=45°．故选：B．分析: 由正方形的性质得出AB=AD，∠BAD=90°，再根据等腰三角形的性质得出∠ABE=∠AEB，∠AED=∠ADE，然后由三角形内角和定理求出∠AEB+∠AED=135°，即可得出∠BEF二、填空题（共5题）16.如图，四边形ABCD为矩形，添加一个条件：_________，可使它成为正方形答案: AB=AD解析：解答: ∵四边形ABCD是矩形，∴当AB=AD或AC⊥BD时，矩形ABCD是正方形．故答案为：AB=AD．分析:由四边形ABCD是矩形，根据邻边相等的矩形是正方形或对角线互相垂直的矩形是正方形，即可求得答案17.已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，其中错误的是_________（只填写序号）答案:②③或①④解析：解答: 有6种选法：（1）①②：由①得有一组邻边相等的平行四边形是菱形，由②得有一个角是直角的平行四边形是矩形，所以平行四边形ABCD是正方形，正确；（2）②③：由②得有一个角是直角的平行四边形是矩形，由③得对角线相等的平行四边形是矩形，所以不能得出平行四边形ABCD是正方形，错误；（3）①③：由①得有一组邻边相等的平行四边形是菱形，由③得对角线相等的平行四边形是矩形，所以平行四边形ABCD是正方形，正确；（4）②④：由②得有一个角是直角的平行四边形是矩形，由④得对角线互相垂直的平行四边形是菱形，所以平行四边形ABCD是正方形，正确；（5）①④：由①得有一组邻边相等的平行四边形是菱形，由④得对角线互相垂直的平行四边形是菱形，所以不能得出平行四边形ABCD是正方形，错误；（6）③④：由③得对角线相等的平行四边形是矩形，由④得对角线互相垂直的平行四边形是菱形，所以平行四边形ABCD是正方形，正确；综上所述：错误的是：②③或①④；故答案为：②③或①④．分析：要判定是正方形，则需能判定它既是菱形又是矩形18.如图，在四边形ABCD中，∠ABC=∠BCD=∠CDA=90°，对角线AC与BD相交于点O．若不增加任何字母与辅助线，要使得四边形ABCD是正方形，则还需增加的一个条件是______答案:答案不唯一如：AB=BC，或AC⊥BD等解析：解答: 由题意可确定，ABCD为一四个角都是90°的四边形，即可能存在矩形的情况，若使AB=AC．可进一步确定其为正方形，故答案为：AB=AC．分析: 要使四边形ABCD是正方形，由题意可知其四个角都是直角，所以还有可能是矩形，使AB=AC，即可满足题意19.如图，在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE=BF，添加一个条件，能证明四边形BECF为正方形的是________①BC=AC；②CF⊥BF；③BD=DF；④AC=BF．答案：①②③解析：解答：∵EF垂直平分BC，∴BE=EC，BF=CF，∵BF=BE，∴BE=EC=CF=BF，∴四边形BECF是菱形；当①BC=AC时，∵∠ACB=90°，则∠A=45°时，菱形BECF是正方形．∵∠A=45°，∠ACB=90°，∴∠EBC=45°∴∠EBF=2∠EBC=2×45°=90°∴菱形BECF是正方形．故选项①正确；当CF⊥BF时，利用正方形的判定得出，菱形BECF是正方形，故选项②正确；当BD=DF时，利用正方形的判定得出，菱形BECF是正方形，故选项③正确；当AC=BF时，无法得出菱形BECF是正方形，故选项④错误．故答案为：①②③．分析: 根据中垂线的性质：中垂线上的点到线段两个端点的距离相等，有BE=EC，BF=FC 进而得出四边形BECF是菱形；由菱形的性质知，以及菱形与正方形的关系，进而分别分析得出即可20.如图，在△ABC中，点D、E、F分别在边AB、BC、CA上，且DE∥CA，DF∥BA．下列四种说法：①四边形AEDF是平行四边形；②如果∠BAC=90°，那么四边形AEDF是矩形；③如果AD平分∠BAC，那么四边形AEDF是菱形；④如果∠BAC=90°，AD平分∠BAC，那么四边形AEDF是正方形．其中，正确的有_________（只填写序号）答案：①②③④解析：解答：∵DE∥CA，DF∥BA，∴四边形AEDF是平行四边形，故①正确；∵四边形AEDF是平行四边形，∠BAC=90°，∴四边形AEDF是矩形，故②正确；∵AD平分∠BAC，四边形AEDF是平行四边形，∴四边形AEDF是菱形，故③正确；∵若AD平分∠BAC，则平行四边形AEDF是菱形，∴若∠BAC=90°，则平行四边形AEDF是正方形，故④正确．故答案为：①②③④．分析: 分别根据平行四边形的判定定理、菱形的判定定理、矩形的判定定理及正方形的判定定理对四个小题进行逐一判断即可三、解答题（共5题）21.如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于点D，交AB于点E，点F在DE的延长线上，且AF=CE．（1）四边形ACEF是平行四边形吗？说明理由；答案：（1）四边形ACEF是平行四边形；∵DE垂直平分BC，∴D为BC的中点，ED⊥BC，又∵AC⊥BC，∴ED∥AC，∴E为AB中点，∴ED是△ABC的中位线．∴BE=AE，FD∥AC．∴BD=CD，∴Rt△ABC中，CE是斜边AB的中线，∴CE=AE=AF．∴∠F=∠5=∠1=∠2．∴∠FAE=∠AEC．∴AF∥EC．又∵AF=EC，∴四边形ACEF是平行四边形；（2）当∠B的大小满足什么条件时，四边形ACEF为菱形？请说明你的结论；答案：（2）当∠B=30°时，四边形ACEF为菱形；理由：∵∠ACB=90°，∠B=30°，∴AC=12 AB，由（1）知CE=12AB，∴AC=CE又四边形ACEF为平行四边形∴四边形ACEF为菱形；（3）四边形ACEF有可能是正方形吗？为什么？答案：解答：（3）四边形ACEF不可能是正方形，∵∠ACB=90°，∴∠ACE＜∠ACB，即∠ACE＜90°，不能为直角，所以四边形ACEF不可能是正方形解析：分析: 本题考查了平行四边形的判定，菱形的判定，垂直平分线的性质，本题中根据特殊角的正弦函数值求∠B的度数是解题的关键22. 如图，在四边形ABCD中，AC、BD交于点O，AO=CO，BO=DO，∠ABC=∠DCB．（1）求证：四边形ABCD是矩形；答案:解答：（1）证明：∵AO=CO，BO=DO，∴四边形ABCD是平行四边形，∴AB∥DC，∴∠ABC+∠DCB=180°，∵∠ABC=∠DCB，∴∠ABC=90°，∴四边形ABCD是矩形；（2）要使四边形ABCD是正方形，请写出AC、BD还需要满足的条件答案:（2）AC⊥BD解析：（2）要使四边形ABCD是正方形，AC、BD还需要满足的条件是：AC⊥BD分析：（1）利用平行四边形的判定方法得出四边形ABCD是平行四边形，进而得出∠ABC=90°，即可得出答案；（2）利用正方形的判定得出矩形的对角线互相垂直进而得出答案23.如图，AB是CD的垂直平分线，交CD于点M，过点M作ME⊥A C，MF⊥AD，垂足分别为E、F．（1）求证：∠CAB=∠DAB；（2）若∠CAD=90°，求证：四边形AEMF是正方形答案：见解答解析：解答：（1）证明：∵AB是CD的垂直平分线，∴AC=AD，又∵AB⊥CD∴∠CAB=∠DAB（等腰三角形的三线合一）；（2）证明：∵ME⊥A C，MF⊥AD，∠CAD=90°，即∠CAD=∠AEM=∠AFM=90°，∴四边形AEMF是矩形，又∵∠CAB=∠DAB，ME⊥A C，MF⊥AD，∴ME=MF，∴矩形AEMF是正方形．分析:本题考查正方形的判定，线段的垂直平分线的性质及等腰三角形的判定与性质的知识，综合性较强24.如图，在正方形ABCD的外侧，作等边三角形ADE，连接BE，CE．（1）求证：BE=CE．答案：解答：(1)证明：∵四边形ABCD为正方形∴AB=AD=CD，∠BAD=∠ADC=90°∵三角形ADE为正三角形∴AE=AD=DE，∠EAD=∠EDA=60°∴∠BAE=∠CDE=150°在△BAE和△CDE中AB＝CD∠BAE＝∠CDEAE＝DE∴△BAE≌△CDE∴BE=CE；（2）求∠BEC的度数答案：∠BEC=30°解析：解答：（2）∵AB=AD，AD=AE，∴AB=AE，∴∠ABE=∠AEB，又∵∠BAE=150°，∴∠ABE=∠AEB=15°，同理：∠CED=15°∴∠BEC=60°-15°×2=30°分析: 本题考查了正方形的性质，（1）利用了正方形的性质，等腰三角形的性质，全等三角形的判定与性质；（2）利用了等腰三角形的判定与性质，角的和差．25.如图，在△ABC中，∠ACB=90°，AC=BC，点D在边AB上，连接CD，将线段CD绕点C顺时针旋转90°至CE位置，连接AE．（1）求证：AB⊥AE．答案：解答：∵∠ACB=90°，∴∠BCD+∠ACD=90°，∵∠DCE=90°，∴∠ACD+∠ACE=90°，∴∠BCD=∠ACE，在△CBD与△CAE中，CB＝CA∠BCD＝∠ACECD＝CE∴△CBD≌△CAE（SAS），∴∠B=∠CAE，∵∠B+∠BAC=90°，∴∠BAC+∠EAC=90°，∴AB⊥AE；（2）若点D为AB中点，求证：四边形ADCE是正方形答案：解答: （2）证明：∵点D为AB中点，∴∠ADC=90°，∵∠DCE=90°，∠BAE=90°，∴四边形ADCE是矩形，∴CD=CE，∴四边形ADCE是正方形解析：分析: 此题主要考查了正方形的判定以及全等三角形的判定与性质等知识，得出∠BCD=∠ACE是解题关键。

19.3.2 正方形的判断与性质一．选择题（共 5 小题）1．以下说法错误的选项是（）A ．有一个角为直角的菱形是正方形B．有一组邻边相等的矩形是正方形C．对角线相等的菱形是正方形D．对角线相等且相互垂直的四边形是正方形2．在正方形 ABCD 的边 AB 、 BC、 CD 、DA 上分别随意取点 E、 F、 G、H ．这样获得的四边形EFGH 中，是正方形的有（）A．1 个 B．2 个 C．4 个 D．无量多个3．如图，四边形ABCD 中， AD=DC ，∠ADC= ∠ABC=90 °，DE ⊥ AB ，若四边形 ABCD 面积为16，则 DE 的长为（）A ． 3B． 2C． 4D． 84．△ ABC 中，∠C=90 °，点 O 为△ ABC 三条角均分线的交点， OD ⊥ BC 于 D ， OE⊥AC 于 E， OF⊥ AB 于 F，且AB=10cm ， BC=8cm ， AC=6cm ，则点 O 到三边 AB 、 AC 、 BC 的距离为（）A ． 2cm， 2cm， 2cmB ．3cm， 3cm， 3cm C． 4cm， 4cm， 4cm D ．2cm， 3cm， 5cm5．如图，在一个大正方形，放入三个面积相等的小正方形纸片，这三纸片遮住的总面积是24 平方厘米，且未遮住的面积比小正方形面积的四分之一还少 3 平方厘米，则大正方形的面积是（单位：平方厘米）（）A．40 B．25C． 26D． 36二．填空题（共 4 小题）6．现有一边长等于 a（ a＞ 16）的正方形纸片，从距离正方形的四个极点8cm 处，沿 45°角画线，将正方形纸片分成 5 部分，则暗影部分是_________（填写图形的形状）（如图），它的一边长是_________ ．7．如图，正方形ABCD的对角线交于点O，以AD为边向外作Rt △ADE ，∠AED=90 °，连结OE， DE=6 ，OE=8 ，则另向来角边AE的长为_________．8．如图，在四边形 ABCD 中，∠ADC= ∠ ABC=90 °， AD=CD ， DP⊥ AB 于 P．若四边形 ABCD 的面积是18，则DP 的长是 _________ ．9．四边形 ABCD 的对角线AC 和 BD 订交于点O，设有以下条件：① AB=AD ；②∠ DAB=90 °；③ AO=CO ，BO=DO ；④矩形 ABCD ；⑤ 菱形 ABCD ，⑥ 正方形 ABCD ，则在以下推理不建立的是_________A、①④ ? ⑥；B、①③ ? ⑤；C、①② ? ⑥；D、②③ ? ④三．解答题（共 11 小题）10．如图，已知点 E、 F、G、 H 分别在正方形 ABCD 的各边上，且 AE=BF=CG=DH ， AF 、 BG 、CH 、 DE 分别订交于点 A ′、B ′、 C′、 D′．求证：四边形 A ′B′C′D′是正方形．11．如图，在正方形 ABCD 中，点 M 在边 AB 上，点 N 在边 AD 的延伸线上，且 BM=DN ．点 E 为 MN 的中点， DE 的延伸线与 AC 订交于点 F．试猜想线段 DF 与线段 AC 的关系，并证你的猜想．12．如图，正方形ABCD 边长为 6．菱形 EFGH 的三个极点E、 G、H 分别在正方形ABCD 的边 AB 、CD、DA 上，且 AH=2 ，连结 CF．（1）当 DG=2 时，求证：菱形 EFGH 为正方形；（2）设 DG=x ，试用含 x 的代数式表示△FCG 的面积．13．如图，正方形ABCD ，动点 E 在 AC 上， AF ⊥ AC ，垂足为 A ， AF=AE ．（1）求证： BF=DE ；（2）当点 E 运动到 AC 中点时（其余条件都保持不变），问四边形 AFBE 是什么特别四边形？说明原因．14．已知，如图，矩形 ABCD 中， AD=6 ， DC=7 ，菱形 EFGH 的三个极点 E， G， H 分别在矩形 ABCD 的边 AB ，CD，DA 上， AH=2 ，连结 CF．（1）若 DG=2 ，求证四边形 EFGH 为正方形；（2）若 DG=6 ，求△ FCG 的面积；（3）当 DG 为什么值时，△ FCG 的面积最小．15．如图，正方形ABCD 中， AC 是对角线，今有较大的直角三角板，一边一直经过点 B ，直角极点P 在射线 AC 上挪动，另一边交DC于Q．（ 1）如图 1，当点 Q 在 DC 边上时，猜想并写出PB 与 PQ 所知足的数目关系；并加以证明；（ 2）如图 2，当点 Q 落在 DC 的延伸线上时，猜想并写出PB 与 PQ 知足的数目关系，请证明你的猜想．16．如图，已知四边形 ABCD 是正方形，分别过 A 、 C 两点作 l1∥ l2，作 BM ⊥ l1于 M ， DN⊥ l 1于 N ，直线 MB 、 ND 分别交 l2于 Q、 P．求证：四边形 PQMN 是正方形．17．在正方形 ABCD 各边前一次截取AE=BF=CG=DH ，连结 EF，FG，GH ，HE．试问四边形EFGH 是不是正方形？18．如图，四边形ABCD 是正方形，点P 是 BC上随意一点，DE⊥ AP于点E，BF⊥AP于点F，CH ⊥ DE于点H，BF 的延伸线交CH 于点 G．（1）求证： AF ﹣ BF=EF ；（2）四边形 EFGH 是什么四边形？并证明；（3）若 AB=2 ， BP=1，求四边形 EFGH 的面积．19．如图，△ ABC 中，∠C=90 °，∠ BAC 、∠ ABC 的均分线订交于点 D，DE⊥ BC ，DF⊥ AC ，垂足分别为 E、F．问四边形 CFDE 是正方形吗？请说明原因．20．如图，在△ABC 中，∠BAC=90 °，AB=AC ，点 D 是 BC 的中点， DE ⊥AB ，DF⊥ AC 垂足分别为E，F．求证：四边形 DEAF 是正方形．19.3.2 正方形的判断与性质参照答案与试题分析一．选择题（共 5 小题）1．以下说法错误的选项是（）A ．有一个角为直角的菱形是正方形B．有一组邻边相等的矩形是正方形C．对角线相等的菱形是正方形D．对角线相等且相互垂直的四边形是正方形考点：正方形的判断．剖析：正方形：四个角都是直角，四条边都相等，对角线相等，且相互垂直均分的平行四边形；菱形：四条边都相等，对角线相互垂直均分的平行四边形；矩形：四个角都相等，对角线相等的平行四边形．解答：解：A 、有一个角为直角的菱形的特点是：四条边都相等，四个角都是直角，则该菱形是正方形．故本选项说确；B、有一组邻边相等的矩形的特点是：四条边都相等，四个角都是直角．则该矩形为正方形．故本选项说确；C、对角线相等的菱形的特点是：四条边都相等，对角线相等的平行四边形，即该菱形为正方形．故本选项说确；D、对角线相等且相互垂直的平行四边形是正方形．故本选项说法错误；应选 D．评论：本题考察了正方形的判断．正方形集矩形、菱形的性质于一身，是特别的平行四边形．2．在正方形 ABCD 的边 AB 、 BC、 CD 、DA 上分别随意取点E、 F、 G、H ．这样获得的四边形EFGH 中，是正方形的有（）A． 1个B．2 个C．4 个D．无量多个考点：正方形的判断与性质；全等三角形的判断．专题：计算题．剖析：在正方形四边上随意取点E、 F、 G、 H，若能证明四边形 EFGH 为正方形，则说明能够获得无量个正方形．解答：解：无量多个．如图正方形ABCD ：AH=DG=CF=BE ， HD=CG=FB=EA ，∠ A= ∠ B=∠ C=∠ D，有△AEH ≌△DHG ≌△CGF≌ △BFE，则 EH=HG=GF=FE ，此外很简单得四个角均为90°则四边形 EHGF 为正方形．应选 D．评论：本题考察了正方形的判断与性质，难度适中，利用三角形全等的判断证明EH=HG=GF=FE ．3．如图，四边形ABCD 中， AD=DC ，∠ADC= ∠ABC=90 °，DE ⊥ AB ，若四边形ABCD 面积为 16，则 DE 的长为（）A．3B．2C．4D．8考点：正方形的判断与性质．专题：证明题．剖析：如图，过点 D 作 BC 的垂线，交 BC 的延伸线于 F，利用互余关系可得∠ A= ∠ FCD ，又∠ AED= ∠ F=90°，AD=DC ，利用 AAS 能够判断△ ADE ≌ △ CDF，∴ DE=DF ， S 四边形ABCD =S 正方形DEBF=16 ， DE=4 ．解答：解：过点 D 作 BC 的垂线，交 BC 的延伸线于 F，∵ ∠ ADC= ∠ ABC=90 °，∠ CDF+ ∠ EDC=90 °，∴∠A=∠FCD ，又∠ AED= ∠ F=90°， AD=DC ，∴△ADE ≌△CDF，∴DE=DF ，S 四边形ABCD =S 正方形DEBF=16 ，∴ DE=4 ．应选 C．评论：本题运用割补法，或许旋转法将四边形ABCD转变为正方形，依据面积保持不变，来求正方形的边长．4．△ ABC 中，∠C=90 °，点 O 为△ ABC 三条角均分线的交点，OD ⊥ BC 于 D ， OE⊥AC 于AB=10cm ， BC=8cm ， AC=6cm ，则点 O 到三边 AB 、 AC 、 BC 的距离为（）A ．2cm， 2cm， 2cmB ．3cm， 3cm， 3cm C．4cm， 4cm， 4cm D ．E， OF⊥ AB 于 F，且2cm，3cm， 5cm考点：正方形的判断与性质．剖析：连结 OA ， OB， OC，利用角的均分线上的点到角的两边的距离相等可知△BDO≌△ BFO，△CDO ≌△ CEO ，△ AEO ≌△ AFO ，∴BD=BF ，CD=CE ，AE=AF ，又因为点 O 到三边 AB 、AC 、BC 的距离是 CD ，∴ AB=8 ﹣ CD+6 ﹣ CD=10 ，解得 CD=2 ，所以点 O 到三边 AB 、 AC 、BC 的距离为 2．解答：解：连结 OA ， OB ， OC，则△ BDO ≌ △ BFO ，△ CDO≌ △ CEO，△ AEO ≌ △AFO ，∴BD=BF ， CD=CE ， AE=AF ，又∵ ∠ C=90， OD⊥ BC 于 D， OE⊥ AC 于 E，且 O 为△ ABC 三条角均分线的交点∴四边形 OECD 是正方形，则点 O 到三边 AB、 AC、BC 的距离 =CD，∴ AB=8 ﹣ CD+6﹣ CD= ﹣ 2CD+14 ，又依据勾股定理可得：AB=10 ，即﹣ 2CD+14=10∴ CD=2 ，即点 O 到三边 AB 、 AC 、 BC 的距离为2cm．应选 A评论：本题主要考察垂直均分线上的点到线段两段的距离相等的性质和边的和差关系．5．如图，在一个大正方形，放入三个面积相等的小正方形纸片，这三纸片遮住的总面积是24 平方厘米，且未遮住的面积比小正方形面积的四分之一还少 3 平方厘米，则大正方形的面积是（单位：平方厘米）（）A． 40B．25C．26D．36考点：正方形的判断与性质．专题：计算题．剖析：设小正方形的边长为a，大正方形的边长为b，由正方形的面积公式，依据题意列出方程组解方程组得出大正方形的边长，则可求出头积．解答：解：设小正方形的边长为a，大正方形的边长为 b，由这三纸片遮住的总面积是24 平方厘米，可得ab+a（ b﹣ a）=24① ，2 2将①②联立解方程组可得：a=4， b=5，∴大正方形的边长为5，∴面积是 25．应选 B．评论：本题考察了正方形的性质及面积公式，难度较大，重点依据题意列出方程．二．填空题（共 4 小题）6．现有一边长等于a（ a＞ 16）的正方形纸片，从距离正方形的四个极点8cm 处，沿 45°角画线，将正方形纸片分成 5 部分，则暗影部分是正方形（填写图形的形状）（如图），它的一边长是cm．考点：正方形的判断与性质．专题：压轴题．剖析：延伸小正方形的一边交大正方形于一点，连结此点与距大正方形极点8cm 处的点，结构直角边长为8的等腰直角三角形，将小正方形的边长转变为等腰直角三角形的斜边长来求解即可．解答：解：如图，作AB 平行于小正方形的一边，延伸小正方形的另一边与大正方形的一边交于 B 点，∴ △ ABC 为直角边长为8cm 的等腰直角三角形，∴AB=AC=8 ，∴暗影正方形的边长 =AB=8cm ．故答案为：正方形， cm．评论：本题考察了正方形的性质与勾股定理的知识，题目同时也浸透了转变思想．7．如图，正方形则另向来角边AE ABCD的长为的对角线交于点10．O，以AD为边向外作Rt △ADE，∠AED=90 °，连结OE， DE=6 ，OE=8 ，考点：正方形的判断与性质；全等三角形的判断与性质；勾股定理．剖析：第一过点 O 作 OM ⊥ AE 于点 M ，作 ON⊥DE ，交 ED 的延伸线于点N，易得四边形EMON 是正方形，点 A ，O， D，E 共圆，则可得△ OEN 是等腰直角三角形，求得EN 的长，既而证得Rt△AOM ≌ Rt△ DON ，得到 AM=DN ，既而求得答案．解答：解：过点 O 作 OM ⊥ AE 于点 M ，作 ON⊥ DE ，交 ED 的延伸线于点N，∵ ∠ AED=90 °，∴四边形 EMON 是矩形，∵正方形 ABCD 的对角线交于点O，∴ ∠ AOD=90 °， OA=OD ，∴ ∠ AOD+ ∠ AED=180 °，∴点 A ，O，D ，E 共圆，∴=，∴∠ AEO= ∠ DEO= ∠ AED=45 °，∴OM=ON ，∴四边形 EMON 是正方形，∴EM=EN=ON ，∴△ OEN 是等腰直角三角形，∵OE=8，∴ EN=8 ，∴EM=EN=8 ，在 Rt△ AOM 和 Rt △ DON 中，，∴Rt△ AOM ≌ Rt△ DON （ HL ），∴AM=DN=EN ﹣ ED=8 ﹣ 6=2，∴AE=AM+EM=2+8=10 ．故答案为： 10．评论：本题考察了正方形的判断与性质、全等三角形的判断与性质以及等腰直角三角形性质．本题难度较大，注意掌握协助线的作法，注意掌握数形联合思想的应用．8．如图，在四边形 ABCD 中，∠ADC= ∠ ABC=90 °， AD=CD ， DP⊥ AB 于 P．若四边形 ABCD 的面积是18，则DP的长是 3 ．考点：正方形的判断与性质；全等三角形的判断与性质．剖析：过点 D 作 DE ⊥ DP 交 BC 的延伸线于E，先判断出四边形DPBE 是矩形，再依据等角的余角相等求出∠ ADP= ∠CDE ，再利用“角角边”证明△ ADP 和△ CDE 全等，依据全等三角形对应边相等可得DE=DP ，而后判断出四边形 DPBE 是正方形，再依据正方形的面积公式解答即可．解答：解：如图，过点 D 作 DE ⊥ DP 交 BC 的延伸线于E，∵ ∠ ADC= ∠ ABC=90 °，∴四边形 DPBE 是矩形，∵ ∠ CDE+ ∠CDP=90 °，∠ADC=90 °，∴ ∠ ADP+ ∠CDP=90 °，∴ ∠ ADP= ∠CDE ，∵DP⊥AB ，∴∠ APD=90 °，∴ ∠ APD= ∠E=90 °，在△ADP 和△ CDE 中，，∴ △ ADP ≌△ CDE （AAS ），∴DE=DP ，四边形 ABCD 的面积 =四边形 DPBE 的面积 =18，∴矩形 DPBE 是正方形，∴DP==3 ．故答案为： 3．评论：本题考察了正方形的判断与性质，全等三角形的判断与性质，熟记各性质并作协助线结构出全等三角形和正方形是解题的重点．9．四边形 ABCD 的对角线 AC 和 BD 订交于点 O，设有以下条件：① AB=AD；②∠ DAB=90 °；③ AO=CO ，BO=DO ；④矩形 ABCD ；⑤ 菱形 ABCD ，⑥ 正方形 ABCD ，则在以下推理不建立的是CA、①④ ? ⑥；B、①③ ? ⑤；C、①② ? ⑥；D、②③ ? ④考点：正方形的判断与性质；全等三角形的判断与性质；菱形的判断与性质；矩形的判断与性质．专题：证明题．剖析：依据矩形、菱形、正方形的判断定理，对角线相互均分的四边形为平行四边形，再由邻边相等，得出是菱形，和一个角为直角得出是正方形，依据已知对各个选项进行剖析从而获得最后的答案．解答：解： A 、由①④得，一组邻边相等的矩形是正方形，故正确；B、由③得，四边形是平行四边形，再由① ，一组邻边相等的平行四边形是菱形，故正确；C、由①②不可以判断四边形是正方形；D、由③得，四边形是平行四边形，再由② ，一个角是直角的平行四边形是矩形，故正确．应选 C．评论：本题用到的知识点是：矩形、菱形、正方形的判断定理，如：一组邻边相等的矩形是正方形；对角线相互均分且一组邻边相等的四边形是菱形；对角线相互均分且一个角是直角的四边形是矩形．灵巧掌握这些判断定理是解本题的重点．三．解答题（共11 小题）ABCD的各边上，且AE=BF=CG=DH，AF、BG、CH、DE分别相10．如图，已知点E、 F、G、 H 分别在正方形交于点 A ′、B ′、 C′、 D′．求证：四边形 A ′B′C′D′是正方形．考点：正方形的判断与性质；全等三角形的判断与性质．专题：证明题．剖析：依照三角形的角和定理能够判断四边形 A ′B′C′D′的三个角是直角，则四边形是矩形，而后证明一组邻边相等，能够证得四边形是正方形．解答：证明：在正方形ABCD 中，∵在△ABF 和△ BCG 中，∴ △ ABF ≌△ BCG （SAS）∴ ∠ BAF= ∠GBC ，∵ ∠ BAF+ ∠AFB=90 °，∴ ∠ GBC+ ∠ AFB=90 °，∴ ∠ BB ′F=90°，∴ ∠ A ′B′C′=90°．∴同理可得∠ B ′C′D′=∠ C′D′A′=90°，∴四边形 A ′B′C′D′是矩形．∵在△AB ′B 和△BC′C 中，∴ △ AB ′B≌ △ BC′C（ AAS ），∴AB ′=BC ′∵在△AA ′E 和△BB ′F中，∴ △ AA ′E≌ △ BB ′F（ AAS ），∴AA ′=BB ′∴A ′B′=B ′C′∴矩形 A ′B′C′D′是正方形．评论：本题考察了正方形的判断，判断的方法是证明是矩形同时是菱形．11．如图，在正方形DE 的延伸线与ACABCD订交于点中，点 M 在边F．试猜想线段AB 上，点DF 与线段N 在边 AD 的延伸线上，且AC 的关系，并证你的猜想．BM=DN．点E 为MN的中点，考点：正方形的判断与性质；全等三角形的判断与性质；线段垂直均分线的性质．专题：研究型．剖析：猜想：线段 DF 垂直均分线段AC ，且 DF=AC ，过点 M 作 MG ∥ AD ，与 DF 的延伸线订交于点 G，作 GH⊥ BC，垂足为 H，连结 AG 、 CG．依据正方形的性质和全等三角形的证明方法证明△AMG ≌ △CHG 即可．解答：猜想：线段 DF 垂直均分线段AC ，且 DF=AC ，证明：过点 M 作 MG ∥ AD ，与 DF 的延伸线订交于点 G．则∠EMG= ∠N，∠BMG= ∠ BAD ，∵ ∠ MEG= ∠ NED ， ME=NE ，∴△MEG ≌△ NED，∴MG=DN ．∵BM=DN ，∴MG=BM ．作 GH⊥ BC，垂足为 H，连结 AG 、CG．∵四边形 ABCD 是正方形，∴ AB=BC=CD=DA ，∠ BAD= ∠ B= ∠ ADC=90 °，∵ ∠ GMB= ∠ B= ∠ GHB=90 °，∴四边形 MBHG 是矩形．∵MG=MB ，∴四边形 MBHG 是正方形，∴MG=GH=BH=MB ，∠ AMG= ∠ CHG=90 °，∴AM=CH ，∴△ AMG ≌ △CHG ．∴GA=GC ．又∵ DA=DC ，∴ DG 是线段 AC 的垂直均分线．∵ ∠ ADC=90 °， DA=DC ，∴DF=AC即线段 DF 垂直均分线段AC ，且 DF=AC ．评论：本题综合考察了矩形的判断和性质、正方形的判断和性质，垂直均分线的判断和性质，全等三角形的性质和判断等知识点，本题综合性比较强，难度较大，但题型较好，训练了学生剖析问题和解决问题以及敢于猜想的能力．12．如图，正方形ABCD 边长为 6．菱形 EFGH 的三个极点E、 G、H 分别在正方形ABCD 的边 AB 、CD、DA 上，且 AH=2 ，连结 CF．（1）当 DG=2 时，求证：菱形 EFGH 为正方形；（2）设 DG=x ，试用含 x 的代数式表示△FCG 的面积．考点：正方形的判断与性质；全等三角形的判断与性质；菱形的性质．剖析：（1）因为四边形ABCD 为正方形，四边形 HEFG 为菱形，那么∠D= ∠A=90 °，HG=HE ，而 AH=DG=2易证△ AHE ≌ △ DGH ，从而有∠ DHG= ∠HEA ，等量代换可得∠ AHE+∠ DHG=90°，易证四边形HEFG 为正方形；（ 2）欲求△ FCG 的面积，由已知得CG 的长易求，只要求出GC 边的高，经过证明△ AHE≌ △ MFG可得．解答：（1）证明：在△ HDG 和△ AEH 中，，∵四边形 ABCD 是正方形，∴ ∠ D=∠ A=90 °，∵四边形 EFGH 是菱形，∴HG=HE ，∵DG=AH=2 ，∴Rt△ HDG ≌ △ AEH ，∴∠ DHG= ∠ AEH ，∴∠ DHG+ ∠ AHE=90 °∴∠ GHE=90 °，∴菱形 EFGH 为正方形；（ 2）解：过 F 作 FM ⊥ CD ，垂足为M ，连结 GE∵CD∥ AB ，∴∠AEG= ∠MGE ，∵GF∥ HE ，∴ ∠ HEG= ∠ FGE，∴∠AEH= ∠FGM，在 Rt△ AHE 和 Rt△ GFM 中，∵ ，∴ Rt△ AHE ≌ Rt△ GFM ，∴MF=2 ，∵ DG=x ，∴CG=6﹣ x．∴S△FCG=CG?FM=6 ﹣ x．评论：作 FM ⊥ DC，交本题考察了正方形的性质、菱形的性质、全等三角形的判断和性质，解题的重点是作协助线：过DC 延伸线于M ，连结 GE，结构全等三角形和错角．F13．如图，正方形ABCD ，动点 E 在 AC 上， AF ⊥ AC ，垂足为 A ， AF=AE ．（1）求证： BF=DE ；（2）当点 E 运动到 AC 中点时（其余条件都保持不变），问四边形 AFBE 是什么特别四边形？说明原因．考点：正方形的判断与性质；全等三角形的判断与性质．剖析：（1）依据正方形的性质判断△ ADE≌△ ABF后即可获得（ 2）利用正方形的判断方法判断四边形AFBE 为正方形即可．BF=DE ；解答：（1）证明： ∵ 正方形 ABCD ，∴ AB=AD ， ∠BAD=90 °，∵AF ⊥AC ，∴ ∠ EAF=90 °，∴ ∠ BAF= ∠EAD ，在△ADE 和△ ABF 中∴ △ ADE ≌ △ ABF （ SAS ），∴ BF=DE ；（ 2）解：当点 E 运动到 AC 的中点时四边形 AFBE 是正方形，原因：∵ 点 E 运动到 AC 的中点， AB=BC ，∴ BE ⊥AC ， BE=AE=AC ，∵ AF=AE ，∴ BE=AF=AE ，又 ∵ BE ⊥ AC ， ∠FAE= ∠ BEC=90 °，∴ BE ∥AF ，∵ BE=AF ，∴ 得平行四边形 AFBE ，∵ ∠ FAE=90 °，AF=AE ，∴ 四边形 AFBE 是正方形．评论：本题考察了正方 形的判断和性质，解题的重点是正确的利用正方形的性质．14．已知，如图，矩形 ABCD 中， AD=6 ， DC=7 ，菱形 EFGH 的三个极点 E ， G ， H 分别在矩形 ABCD 的边 AB ，CD ， DA 上， AH=2 ，连结 CF ．（ 1）若 DG=2 ，求证四边形 EFGH 为正方形；（ 2）若 DG=6 ，求 △ FCG 的面积；（ 3）当 DG 为什么值时， △ FCG 的面积最小．考点： 正方形的判断与性质；全等三角形的判断与性质；菱形的性质；矩形的性质．专题： 计算题；压轴题．剖析： （1）因为四边形 ABCD 为矩形， 四边形 HEFG 为菱形，那么 ∠D= ∠A=90 °，HG=HE ，而 AH=DG=2 ，易证 △ AHE ≌ △ DGH ，从而有 ∠ DHG= ∠HEA ，等量代换可得 ∠ AHE+ ∠ DHG=90 °，易证四边形 HEFG 为正方形； （ 2）过 F 作 FM ⊥ DC ，交 DC 延伸线于 M ，连结 GE ，因为 AB ∥ CD ，可得 ∠ AEG= ∠ MGE ，同理有 ∠ HEG= ∠ FGE ，利用等式性质有 ∠ AEH= ∠ MGF ，再联合 ∠ A= ∠ M=90 °，HE=FG ，可证 △ AHE ≌ △ MFG ，从而有 FM=HA=2 （即无论菱形 EFGH 怎样变化，点 F 到直线 CD 的距离一直为定值 2），从而可求三角形面积；HE 2≤53，在 Rt △ DHG （ 3）先设 DG=x ，由第（ 2）小题得， S △FCG =7﹣ x ，在△ AHE 中，AE ≤AB=7 ，利用勾股定理可得中，再利用勾股定理可得x 2+16≤53，从而可求 x ≤，从而可适当 x=时， △ GCF 的面积最小． 解答： 解：（ 1） ∵四边形 ABCD 为矩形，四边形 HEFG 为菱形，∴ ∠ D=∠ A=9 0°， HG=HE ，又 AH=DG=2 ，∴ Rt △ AHE ≌ Rt △ DGH （HL ），∴ ∠ DHG= ∠ HEA ，∵ ∠ AHE+ ∠ HEA=90 °，∴ ∠ AHE+ ∠ DHG=90 °，∴ ∠ EHG=90 °，∴ 四边形 HEFG 为正方形；（ 2）过 F 作 FM ⊥DC ，交 DC 延伸线于 M ，连结 GE ，∵AB ∥CD ，∴∠AEG= ∠MGE ，∵ HE ∥ GF ，∴ ∠ HEG= ∠ FGE ，∴∠AEH= ∠MGF ，在 △ AHE 和 △ MFG 中， ∠ A= ∠M=90 °，HE=FG ， ∴△AHE ≌△MFG ，∴ FM=HA=2 ，即不论菱形 EFGH 怎样变化，点 F 到直线 CD 的距离一直为定值 2，所以；（ 3）设 DG=x ，则由第（ 2）小题得， S △ FCG =7﹣ x ，在 △AHE 中， AE ≤AB=7 ，∴ HE 2≤53，∴ x 2+16≤53，∴ x ≤，∴ S △FCG 的最小值为，此时 DG= ，∴ 当 DG= 时， △ FCG 的面积最小为（） ．评论： 本题考察了矩形、菱形的性质、全等三角形的判断和性质、勾股定理．解题的重点是作协助线：过F 作 FM ⊥ DC ，交 DC 延伸线于 M ，连结 GE ，结构全等三角形和错角．15．如图，正方形 ABCD 中， AC 是对角线，今有较大的直角三角板，一边一直经过点 B ，直角极点P 在射线 AC 上挪动，另一边交 DC 于Q ．（ 1）如图 1，当点 Q 在 DC 边上时，猜想并写出 PB 与 PQ 所知足的数目关系；并加以证明；（ 2）如图 2，当点 Q 落在 DC 的延伸线上时，猜想并写出 PB 与 PQ 知足的数目关系，请证明你的猜想．考点： 正方形的判断与性质；全等三角形的判断与性质．剖析： （1）过 P 作 PE ⊥BC ， PF ⊥ CD ，证明 Rt △ PQF ≌ Rt △ PBE ，即可；（ 2）证明思路同（ 1）解答： （1） PB=PQ ，证明：过 P 作 PE ⊥ BC ， PF ⊥ CD ，∵ P ， C 为正方形对角线 AC 上的点，∴ PC 均分 ∠ DCB ， ∠ DCB=90 °，∴ PF=PE ，∴ 四边形 PECF 为正方形，∵ ∠ BPE+∠ QPE=90°， ∠ QPE+∠ QPF=90 °，∴ ∠ BPE=∠ QPF ，∴ Rt △ PQF ≌ Rt △PBE ，∴ PB=PQ ；（ 2） PB=PQ ，证明：过 P 作 PE⊥ BC ， PF⊥ CD ，∵ P， C 为正方形对角线AC 上的点，∴PC 均分∠ DCB ，∠ DCB=90 °，∴PF=PE，∴四边形 PECF 为正方形，∵ ∠ BPF+∠ QPF=90°，∠ BPF+ ∠ BPE=90 °，∴ ∠ BPE=∠ QPF，∴Rt△ PQF≌ Rt△PBE，∴PB=PQ ．本题考察了正方形，角均分线的性质，以及全等三角形判断与性质．本题综合性较强，注意数形结评论：合思想．16．如图，已知四边形 ABCD 是正方形，分别过 A 、 C 两点作 l1∥ l2，作 BM ⊥ l1于 M ， DN⊥ l 1于 N ，直线 MB 、 ND 分别交 l2于 Q、 P．求证：四边形 PQMN 是正方形．考点：正方形的判断与性质．专题：证明题；压轴题．剖析：可由 Rt△ ABM ≌Rt△ DAN ， AM=DN同理可得 AN=NP ，所以 MN=PN ，从而可得其为正方形．解答：证明： l1∥ l2， BM ⊥ l 1， DN ⊥ l2，∴ ∠ QMN= ∠P=∠ N=90 °，∴四边形 PQMN 为矩形，∵AB=AD ，∠ M= ∠ N=90 °∠ADN+ ∠ NAD=90 °，∠ NAD+∠BAM=90 °，∴∠ADN= ∠BAM ，又∵ AD=BA ，∴Rt△ ABM ≌ Rt△DAN （ AAS ），∴AM=DN同理 AN=DP ，∴AM+AN=DN+DP ，即 MN=PN ．∴四边形 PQMN 是正方形．评论：本题考察了矩形的判断和性质、全等三角形的判断和性质以及正方形的判断，解题的重点是娴熟掌握各样几何图形的性质和判断方法．17．在正方形 ABCD 各边前一次截取AE=BF=CG=DH ，连结 EF，FG，GH ，HE．试问四边形EFGH 是不是正方形？考点：正方形的判断与性质．剖析：依据正方形的性质可得 AB=BC=CD=AD，∠ A= ∠ B= ∠C=∠D ，而后求出 BE=CF=DG=AH ，再利用“边角边”证明△AHE 和△ BEF 和△ CFG 和△ DGH 全等，依据全等三角形对应边相等可得EF=FG=GH=EH ，全等三角形对应角相等可得∠ AHE= ∠ BEF= ∠ CFG= ∠ DGH ，再求出∠ EFG=∠ FGH= ∠ GHE= ∠ FEH=90 °，从而获得四边形EFGH 是正方形．解答：解：四边形 EFGH 是正方形．原因以下：∵四边形 ABCD 是正方形，∴AB=BC=CD=AD ，∠ A= ∠ B=∠ C= ∠D ，∵AE=BF=CG=DH ，∴AB ﹣ AE=BC ﹣ BF=CD ﹣CG=AD ﹣ DH ，即 BE=CF=DG=AH ，∴△ AHE ≌ △ BEF≌ △CFG≌ △DGH ，∴EF=FG=GH=EH ，∠ AHE= ∠ BEF= ∠ CFG= ∠ DGH ，∴∠ EFG= ∠ FGH= ∠ GHE= ∠ FEH=90 °，∴四边形 EFGH 是正方形．评论：本题考察了正方形的判断与性质，全等三角形的判断与性质，熟记各性质并求出被截取的四个小直角三角形全等是解题的重点．18．如图，四边形 ABCD 是正方形，点 P 是 BC 上随意一点， DE⊥ AP 于点 E， BF ⊥ AP 于点 F，CH ⊥ DE 于点 H， BF 的延伸线交 CH 于点 G．（1）求证： AF ﹣ BF=EF ；（2）四边形 EFGH 是什么四边形？并证明；考点：正方形的判断与性质；全等三角形的判断与性质；剖析：（1）利用全等三角形的判断第一得出△ AED≌△ BFA，从而得出AE=BF ，即可证明结论；（2）第一得出四边形 EFGH 是矩形，再利用△AED ≌△ BFA ，同理可得：△ AED ≌ △ DHC ，从而得出 EF=EH ，即可得出答案；解答：（1）证明：∵ DE⊥ AP 于点 E， BF⊥ AP 于点 F， CH ⊥DE 于点 H，∴ ∠ AFB= ∠AED= ∠DHC=90 °，∴ ∠ ADE+ ∠ DAE=90 °，又∵ ∠ DAE+ ∠ BAF=90 °，∴∠ADE= ∠BAF ，在△AED 和△ BFA 中，，∴△AED ≌△BFA，∴AE=BF ，∴AF ﹣ AE=EF ，即 AF ﹣ BF=EF ；（ 2）证明：∵ ∠ AFB= ∠AED= ∠DHC=90 °，∴四边形 EFGH 是矩形，∵ △ AED ≌ △ BFA ，同理可得：△ AED≌ △ DHC，∴△AED ≌△BFA≌ △DHC，∴DH=AE=BF ， AF=DE=CH ，∴DE﹣ DH=AF ﹣ AE ，∴EF=EH ，∴矩形 EFGH 是正方形；19．如图，△ ABC 中，∠C=90 °，∠ BAC 、∠ ABC 的均分线订交于点 D，DE⊥ BC ，DF⊥ AC ，垂足分别为 E、F．问四边形 CFDE 是正方形吗？请说明原因．考点：正方形的判断；角均分线的性质．剖析：第一利用垂直的定义证得四边形该四边形是正方形．解答：证明：∵ ∠C=90 °， DE ⊥BC ∴四边形 DECF 为矩形，∵ ∠ A 、∠ B 的均分线交于点D，于点CFDE 是矩形，而后利用角均分线的性质获得E， DF⊥ AC 于点 F，DE=DF ，从而判断∴DF=DE ，∴四边形 CFDE 是正方形．评论：本题主要考察了角均分线的性质，三角形的切圆与心，解题的重点是利用正方形的判断方法证得四边形 CFDE 是正方形．20．如图，在△ABC 中，∠BAC=90 °，AB=AC ，点 D 是 BC 的中点， DE ⊥AB ，DF⊥ AC 垂足分别为E，F．求证：四边形 DEAF 是正方形．考点：正方形的判断；全等三角形的判断与性质．专题：证明题．剖析：由题意先证明□AEDF 是矩形，再依据两角及其一角的对边对应相等来证组对边相等的矩形证明□AEDF 是正方形．解答：证明：∵DE⊥AB ，DF⊥AC△ BDE ≌ △ CDF，依占有一∴ ∠ AED=90 °，∠ AFD=90 °∵ ∠ BAC=90 °∴ ∠ EDF=90 °∴ □AEDF 是矩形在△BDE 和△ CDF 中∵ AB=AC∴ ∠ ABC= ∠ ACB∵DE⊥ AB ， DF⊥ AC∴ ∠ DEB= ∠DFC又∵D 是 BC 的中点∴BD=DC∴△ BDE ≌△ CDF∴DE=DF∴□AEDF 是正方形评论：本题考察的是正方形的判断方法，考察了矩形、全等三角形等基础知识的灵巧运用，鉴别一个四边形是正方形主假如依据正方形的定义及其性质．。

C． 2
D． 5 1
18．如图，正方形 ABCD 中，AD 5，点 E 、F 是正方形 ABCD 内的两点，且 AE FC 4 ，
BE DF 3，则以 EF 为直径的圆的面积为 ( )
A． 1 2
B． 3 5
C． 3 4
D．
19．如图，在平面直角坐标系中，正方形 A1B1C1D1 、D1E1E2B2 、A2 B2C2 D2 、D2 E3E4 B3 、A3B3C3D3 ，
D．16
21．如图，在正方形 ABCD 中，对角线 AC ，BD 相交于点 O ，E ，F 分别在 OD ，OC 上，
且 DE CF ，连接 DF ， AE ， AE 的延长线交 DF 于点 M ，则下列四个结论中正确结 论的个数是 ( )
① AE DF ；
② AM DF ；
③ DAE CDF ；
．
38．如图，正方形 ABCD 中， AB 12 ，点 E 在边 CD 上，CD 3DE ．将 ADE 沿 AE 对折
至 AFE ，延长 EF 交边 BC 于点 G ，连接 AG ，CF ．则下列结论正确的是
．
① ABG AFG ； ② BG GC ；
为
．
31．如图，RtABC 中，C 90 ，AC 2 ，BC 1 ，以斜边为一边向右上方作正方形 ABDE ，
连接 CD ，则 CD 的长为
．
32．如图，将正方形 OABC 放在平面直角坐标系中， O 是坐标原点，点 A 的坐标是 (2,3) ，
则 C 点坐标是
．
33．如图，在平面直角坐标系中，点 A 的坐标是 (0,3) ，点 B 的坐标是 (4,0) ，以 AB 为边
正方形性质与判定练习
1．如果要证明平行四边形 ABCD 为正方形，那么我们需要在四边形 ABCD 是平行四边形的 基础上，进一步证明 ( )

(完整版)正方形的性质与判定习题
正方形是几何形状中的一种特殊情况，具有独特的性质和特点。

本文将为您提供关于正方形性质和判定的一些题，帮助您更好地理
解和应用正方形的相关知识。

题一：基本概念与性质
1. 正方形的定义是什么？它有哪些特点？
2. 正方形的边长和周长之间的关系是什么？
3. 正方形的对角线之间有什么关系？
4. 正方形的面积和边长之间的关系是什么？
题二：正方形的判定
1. 已知一个四边形的四个角都是直角，如何判定这个四边形是
正方形？
2. 已知一个四边形的两组对边相等且相邻边垂直，如何判定这
个四边形是正方形？
3. 已知一个四边形的一组对边相等且两组对边平行，如何判定
这个四边形是正方形？
4. 如何判定一个平行四边形是正方形？
题三：正方形的应用
1. 在平面坐标系中，如何表示一个正方形的顶点坐标？
2. 如何计算一个正方形的面积和周长？
3. 如果一个矩形的长度和宽度相等，能否判定该矩形为正方形？为什么？
以上是关于正方形性质与判定的一些题，希望能够帮助您巩固
对正方形的相关知识。

通过解答这些题，您将能更深入地理解正方
形的特点和应用，为解决相关问题提供有效的方法。

> 注意：本文所提供的内容仅供参考，请在参考后自行验证并
确认。