第三章 晶格振动与晶体的热学性质
- 格式:docx
- 大小:1.14 MB
- 文档页数:17




第三章晶格振动与晶体的热学性质第三章晶格振动与晶体的热学性质晶体中的格点表示原子的平衡位置,晶格振动便是指原子在格点附近的振动。
晶格振动对晶体的电学、光学、磁学、介电性质、结构相变和超导电性都有重要的作用。
本章的主题用最邻近原子间简谐力模型来讨论劲歌振动的本征频率;并用格波来描述晶体原子的集体运动;再用量子理论来表述格波相应的能量量子、3.1 连续介质中的波波动方程22220u ux Y tρ??-=??对足够长的介质,求行波的解:s v q ω=其中波相速ω=称作色散关系。
3.2 一维晶格振动格波讨论晶格振动时采用了绝热近似,近邻近似和简谐近似。
绝热近似:考虑离子运动时,可以近似认为电子很快适应离子的位置变化。
为简单化,可以将离子的运动看成是近似成中性原子的运动。
近邻近似:在晶格振动中,只考虑最近邻的原子间的相互作用;简谐近似:在原子的互作用势能展开式中,只取到二阶项。
0020021()()()()......2r r dU d U U r U r dr dr δ+=+++简谐近似——振动很微弱,势能展式中作二级近似:00'''001()()||2r r U r U r U U δ+=++相邻原子间的作用力02222,r Ud U d U f dr dr δβδβδ=-=-=-= ? ??????一维晶格振动格波考虑第n 个例子的受力情况,它只受最近邻粒子的相互作用即分别受到来自第n-1个粒子及第n+1个例子的弹性力11()n n n f u u β--=-- 11()n n n f u u β++=--1111(2)n n n n n n f f f u u u β-++-=-=--- 2112(2)n n n n d uf ma m u u u dtβ+-===---试探解以行波作试探解()i t naq nq u Ae ω-=2()()(2)i t naq i t naq iaq iaq m e e e e ωωωβ----=---利用:222cos()24sin (/2)iaq iaq e e qa qa -+-=-=得224sin (/2)qa m βω=,/2)qa ω=色散关系 s i n (/2)qa ω=长波极限因为色散曲线是周期的且关于原点对称,在0/q a π<<的区间内,频率仅覆盖在0m ωω<<的范围内。



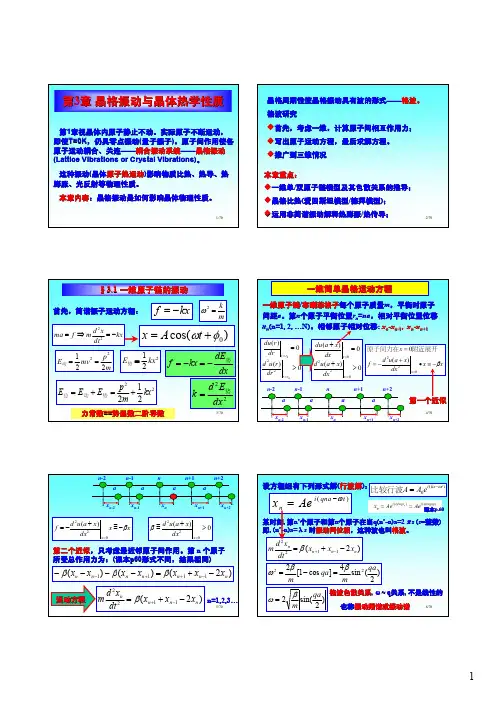

固体物理第三章晶格振动与晶体热学性质第三章晶格振动与晶体的热学性质晶格振动是描述原子在平衡位置附近的振动,由于晶体内原子间存在着相互作用力,各个原子的振动也不是孤立的,而是相互联系的,因此在晶体内形成各种模式的波。
只有当振动微弱时,原子间非谐的相互作用可以忽略,即在简谐近似下,这些模式才是独立的。
由于晶格的周期性条件,模式所取的能量值不是连续的而是分立的。
对于这些独立而又分立的振动模式,可以用一系列独立的简谐振子来描述。
和光子的情形相似,这些谐振子的能量量子称为声子。
这样晶格振动的总体就可以看成声子系综。
若原子间的非谐相互作用可以看作微扰项,则声子间发生能量交换,并且在相互作用过程中,某些频率的声子产生,某些频率的声子湮灭。
当晶格振动破坏了晶格的周期性,使电子在晶格中的运动受到散射而电阻增加,可以看作电子受到声子的碰撞,晶体中的光学性质也与晶格振动有密切关系,在很大程度上可以看作光子与声子的相互作用乃至强烈耦合。
晶格振动最早是用于研究晶体的热学性质,其对晶体的电学性质、光学性质、超导电性、磁性、结构相变等一系列物理问题都有相当重要的作用,是研究固体宏观性质和微观过程的重要基础。
ωη§3-1 简谐近似和简正坐标由原子受力和原子间距之间的关系可以看出,若离开平衡位置的距离在一定限度,原子受力和该距离成正比。
这时该振动可以看成谐振动.用n μϖ表示原子偏离平衡位置(格点)位移矢量,对于三维空间,描述N 个原子的位移矢量需要3N 个分量,表为)3,,2,1(N i i Λ=μ将体系的势函数在平衡位置附近作泰勒展开:高阶项+∑⎪⎪⎭⎫ ⎝⎛∂∂∂+∑∂∂+===j i N j i j i i N i i V V V V μμμμμμ031,2031021)(第一项为平衡位置的势能,可取为零,第二项为平衡位置的力,等于零。
若忽略高阶项,因为势能仅和位移的平方成正比,即为简谐近似。
23121i N i i m T μ&∑==引入合适的正交变换,将动能和势能用所谓的简正坐标表示成仅含平方∑==N j j ij i i Q a m 31μ项而没有交叉项,即:由分析力学,基本形式的拉格朗日方程为:)32,1(,N i q Q T Q T dt d i i i Λ&==∂∂-⎪⎪⎭⎫ ⎝⎛∂∂其中)32,1(,1N i q f q i j N j j i Λϖϖ=∂∂⋅∑==μ朗日方程:)32,1(,0N i Q L Q L dt d i i Λ&==∂∂-⎪⎪⎭⎫ ⎝⎛∂∂则正则方程为:)3,2,1(,02N i Q Q i i i Λ&&==+ω其解为:)sin(δω+=t A Q i i 当考察某一个j Q 时,则:)sin(δωμ+=t A m a j i iji 晶体参与的振动,且它们的振动频率相同。

第三章 晶格振动与晶体的热学性质晶体中的格点表示原子的平衡位置,晶格振动便是指原子在格点附近的振动。
晶格振动对晶体的电学、光学、磁学、介电性质、结构相变和超导电性都有重要的作用。
本章的主题用最邻近原子间简谐力模型来讨论劲歌振动的本征频率; 并用格波来描述晶体原子的集体运动;再用量子理论来表述格波相应的能量量子、3.1 连续介质中的波 波动方程22220u u x Y tρ∂∂-=∂∂对足够长的介质,求行波的解:s v q ω=其中波相速ω=称作色散关系。
3.2 一维晶格振动格波 讨论晶格振动时采用了绝热近似,近邻近似和简谐近似。
绝热近似:考虑离子运动时,可以近似认为电子很快适应离子的位置变化。
为简单化,可以将离子的运动看成是近似成中性原子的运动。
近邻近似:在晶格振动中,只考虑最近邻的原子间的相互作用; 简谐近似:在原子的互作用势能展开式中,只取到二阶项。
0020021()()()()......2r r dU d U U r U r dr dr δ+=+++ 简谐近似——振动很微弱,势能展式中作二级近似:00'''001()()||2r r U r U r U U δ+=++ 相邻原子间的作用力02222,r U d U d U f dr dr δβδβδ⎛⎫⎛⎫∂=-=-=-= ⎪ ⎪∂⎝⎭⎝⎭一维晶格振动格波考虑第n 个例子的受力情况,它只受最近邻粒子的相互作用即分别受到来自第n-1个粒子及第n+1个例子的弹性力11()n n n f u u β--=--11()n n n f u u β++=--1111(2)n n n n n n f f f u u u β-++-=-=---2112(2)n n n n d u f ma m u u u dtβ+-===---试探解 以行波作试探解()i t naq nq u Ae ω-=2()()(2)i t naq i t naq iaq iaq m e e e e ωωωβ----=---利用:222cos()24sin (/2)iaq iaq e e qa qa -+-=-=得224sin (/2)qa m βω=,/2)qa ω=色散关系 s i n (/2)qa ω=长波极限因为色散曲线是周期的且关于原点对称,在0/q a π<<的区间内,频率仅覆盖在0m ωω<<的范围内。
类似于机械低通滤波器,仅在这一范围内的频率可以通过。
在长波极限时:2/0q πλ=→;sin x x →,sin(/2)|(/2)m s qa a q v q ωω====(/2),s m m v a ωω==长波极限时为线性关系,连续介质情形。
布里渊区边界在长波极限时:2/0,q a πλλ=→>>,原子同相运动邻近原子产生恢复力小,频率小在/,2q a a πλ==时,相邻原子反相运动,恢复力取极大,此时,频率取极大值。
空间的对称性:第一布里渊区a)色散关系()q ω的周期对称性,其周期为2/a π,(2/)()q a q ωπω+=色散关系:频率与波矢之间的关系晶格中原子振动存在固定位相关系的平面波称为格波。
格波:在晶体中存在着角频率为ω的平面波→简谐平面波2qπλ=格波的波矢:2q n πλ=⋅格波的传播方向:n 波速:p V q ω= 2,2,2v f f T qλωπλλωπλπ==⋅=⋅== '2h q q K q h a π=+=+ 2h K ha π=是一维晶格的倒格矢,h 为任意整数,则 ''()()(2)i t q na i t qna i h n n n u Ae Ae e u ωωπ---⋅===q 可限制在简约布里渊区 q a a ππ-<≤对于简谐波而言,波速是指相位的传播速度,它等同于能量和波形的传播速度,而大多数的媒质是具有色散的,即:波在这种媒质中的速度与其频率有关,各个简谐波分量具有不同的相速,所以对于非简谐波,例如有限长波列来说,“波速”的意义就含糊不清了,此时我们应以群速来描述局限在有限范围的波列——波包的传播速度。
位相和群速度 波速,相速:p v qω=群速:波包(能量)传播速度。
对三维情况:()g v grad q ωω= ()g q v qω∂=∂ 对非连续晶格,在长波极限时,群速等于相速,且它们都等于声速;此时,点阵的行为象一个连续体,没有色散发生。
随着波长的变短,群速减少,到短波极限/q p a =时减至0。
群速为零的物理意义由于邻近原子振动的位相差为qa ,即邻近原子散射的子波的位相差为π,故被B 反射的子波到达A ,与被A 反射的子波时,他们的位相相同(或相差2π的整数倍)。
在/q a π=处,所有的散射子波相长的干涉结果反射取极大值。
这与X 射线中的布拉菲格条件相同,只不过这里是弹性波。
周期性边界条件引入周期性边界条件,即第1个原子和第N+1个原子的振动完全相同:(1)(1)u u N =+,即(1)iqa i N qa Ae Ae --+=或()1i Nqa Ae -= 有:2,0,1,2,...q n n Naπ==±±整数。
在第一布里渊区,//a q a ππ-<≤,对应于/2/2N n N -<≤,故n 只能取N 个值。
每个波矢在第一布里渊区占的线度2q Naπ=第一布里渊区的线度2a π第一布里渊区状态数2//a N a Naπ= 第一布里渊区中的模数:q 的值唯一地描述了所有的晶格振动模式,因此,这些值的数目必须等于晶格的自由度数N 。
3.3 一维双原子晶格写出双原子运动方程2212212122212212222(2)(2)n n n n n n n n d u m u u u dt d u m u u u dtββ+-+++=---=---行波试探解:21122222cos()02cos()2A m aq A aq m ωβββωβ⎛⎫-⎛⎫= ⎪ ⎪-⎝⎭⎝⎭ ((2))21((21))212i t na q n i t n aq n u Ae u A e ωω--++⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭上式是一个齐次方程,只有其矩阵行列式为零时才有非零解,于是有久期方程:24222112122222cos()2()4sin ()02cos()2m aq m m m m aq aq m ωββωβωββωβ-=-++=-212ω=1/2221212221212()411sin ()()m m m m aq m m m m ωβω+-⎧⎫⎫⎡⎤+⎪⎪=±-⎬⎨⎬⎢⎥+⎣⎦⎭⎪⎪⎩⎭βμ=±1212m m m m μ=+;12M m m =+讨论有两支色散关系:声学支和光学支声学支处于低频;光学支处于高频:13110s ω-->,处于红外区,它具有吸收,反射等性质;在光学支与声学支之间存在一间隙,即晶格不能传播这样的波,因此,双原子晶格起到带通机械滤波器的作用。
声学支与光学支声学支与单原子晶格的结果相似,在长波极限时为连续介质中的情况;而在布里渊区边界/2a π处达到极大值1/22(2/)m β,它对应于质量大的原子振动(而质量小的不动)模式;对光学支,色散关系在布里渊区边界/2a π处达到极小值1/21(2/)m β,它对应于质量小的原子振动(而质量大的不动)模式;在0q =处取极大值1/2(2/)βμ,它对应于邻近两原子的反向运动模式。
长波极限的声学支和光学支长光学支格波与长声学支格波本质上有何差别?长光学支格波的特征是每个原胞内的不同原子做相对振动,振动频率较高,它包含了晶格振动频率最高的振动模式。
{长波极限时,,0a q λ>>→,ω+→22111222cos A m m A aq m ωββ++⎛⎫-=-=- ⎪⎝⎭,在0q →时,两种原子振动有完全相反的位相,长光学波的极限实际上是相邻两种格子的相对振动,且振动中保持它们的质心不变}长声学支格波的特征是原胞内的不同原子没有相对位移,原胞做整体运动,振动频率低,它包含了晶格振动频率最低的振动频率,波速是一常数,任何晶体都存在声学支格波,但简单晶格(非复式格子)晶体不存在光学支格波。
讨论对12m m =,过渡到一维简单格子;布里渊区与模数:【注意实际点阵的周期是2a 而不是a ,第一布里渊区在/2/2a q a ππ-<<之间。
】由周期性边界条件得:(2)2N aq n π=,n =整数,2/22/q n N a n L ππ==(2L N a =),2/222n N a a a πππ-<≤,22N N n -<≤,n 共取N 个值;共两支格波,故频率的数目(模数)2N ==自由度数。
由此可推: 格波波矢的数目=晶体原胞数格波频率的数目=晶体的自由度数(模数)当基元有s 个原子时,模数有sN 个=自由度数。
态密度在k 空间中,由周期性边界条件可知,3(2/)L π体积内允许存在一个态,即关于q 的态密度为:33()(/2)/8q L V ρππ==()()dq d dS q d d ωρωωρωω=⎰⎰ 一般形式:3()(2)g VdS v ωρωπ=⎰⎰ ,/g v d dq ω= 课堂练习11.什么叫简正振动模式?简正振动数目、格波数目或格波振动模式数目是否是一回事?2.在三维晶体中,格波波矢的数目或格波独立的q点数,声学波支数,光学波支数,格波总支数分别等于多少?3.长光学支格波与长声学支格波本质上有何差别?4.长光学纵波,长声学格波能否导致离子晶体的宏观极化?晶格振动的量子化晶格振动是晶体中诸原子(离子)集体地在作振动,其结果表现为晶格中的格波,一般而言,格波不是简谐的,但可以展为正交归一的简谐平面波的线性叠加。
当振动微弱时,格波可近似为简谐波,这时,各格波间的相互作用可以忽略,这就是格波的独立模式。
晶格的周期性及平移对称性是的独立的模式亦即独立的振动是分立的。
因此,我们可以用独立简谐振子的振动来表述格波的独立模式,这就是声子。
声子声子就是晶格振动中的简谐振子的能量量子。
[()1/2]()n q q εω=+声子是一种集体激发的振动形式:其能量为()j q ω ; 对非简谐振动系统,则声子与声子之间就存在着相互作用。
声子的性质声子的粒子性光子——电磁波的能量量子。
电磁波可以认为是光子流,光子携带电磁波的能量和动量,随着光子的运动,有物质的迁移。
声子——声子代表原子的振动状态,不与物质的迁移相联系,因而不携带动量。
声子不是实际存在的实物粒子,通常称为准粒子。
声子虽不携带物理动量,但由德布罗意关系,可以假设它具有准动量,其量值由下式给出:2/s s sshhP q q λπ=== 式中,s q 是声子的波矢值。