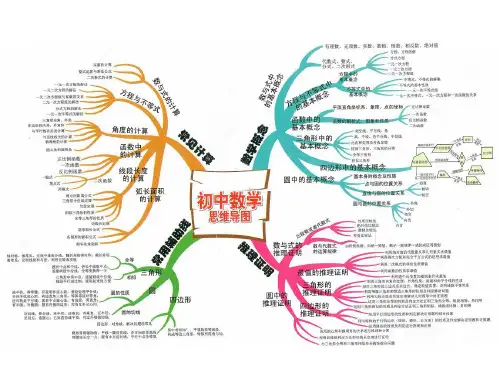
九年级数学思维导图 二次函数的思维导图-二次函数章节知识结构图

初中数学《二次函数》课程教学设计以及思维导图一、教学设计1. 教学目标- 理解二次函数的定义及性质；- 掌握二次函数的图像特征和基本变换；- 能够求解二次函数的零点和最值；- 运用二次函数解决实际问题。

2. 教学内容- 二次函数的定义及性质；- 二次函数的图像特征和基本变换；- 二次函数的零点和最值；- 二次函数在实际问题中的应用。

3. 教学方法- 组织讲解：通过讲解二次函数的定义和性质，介绍二次函数的图像特征和基本变换；- 案例分析：通过具体案例分析，引导学生探索二次函数的零点和最值的求解方法；- 实际应用：引导学生运用二次函数解决实际问题，提高他们的数学建模能力。

4. 教学步骤第一步：导入- 通过引入一个与学生生活相关的问题，激发学生对二次函数的兴趣和思考，如：小明从家里出发骑自行车去学校，他的行程可以用二次函数表示吗？第二步：讲解- 介绍二次函数的定义和性质，包括二次函数的标准形式、顶点形式和描点法；- 解释二次函数的图像特征，包括开口方向、顶点坐标和对称轴；- 讲解二次函数的基本变换，包括平移、伸缩和翻转。

第三步：案例分析- 通过具体案例分析，引导学生探索二次函数的零点和最值的求解方法，包括利用图像、代数方法和函数性质等；- 给学生一些练习题，让他们独立思考和解决问题。

第四步：实际应用- 引导学生运用二次函数解决一些实际问题，如：抛物线的应用、物体的抛射运动等；- 鼓励学生分组合作，进行数学建模和实际问题求解。

第五步：总结与拓展- 对本节课所学内容进行总结，强调关键概念和解题方法；- 提供一些拓展性问题，让学生进一步思考和探索。

5. 教学评价- 通过学生课堂表现、小组讨论、个人作业等方式进行评价；- 评估学生对二次函数定义及性质的理解程度；- 评估学生对二次函数图像特征和基本变换的掌握程度；- 评估学生对二次函数零点和最值求解方法的应用能力；- 评估学生在实际问题中运用二次函数解决问题的数学建模能力。

初中数学《二次函数》课程教学设计以及思维导图1. 教学目标1.1 知识与技能- 理解二次函数的定义及其一般形式；- 学会用顶点式、标准式表示二次函数；- 掌握二次函数的图像特征，如开口方向、对称轴等；- 能够运用二次函数解决实际问题。

1.2 过程与方法- 通过实例认识二次函数的图像特点；- 学会利用配方法、公式法求解二次方程；- 学会利用二次函数的性质解决实际问题；- 培养学生的逻辑思维能力和解决问题的能力。

1.3 情感态度与价值观- 培养学生对数学的兴趣和自信心；- 培养学生积极思考、合作探讨的学习态度；- 培养学生运用数学知识解决实际问题的能力。

2. 教学内容2.1 二次函数的定义与一般形式- 二次函数的定义：形如`y=ax^2+bx+c(a≠0, a, b, c为常数)`的函数称为二次函数；- 二次函数的一般形式：`y=a(x-h)^2+k`，其中`(h, k)`为顶点坐标。

2.2 二次函数的图像特征- 开口方向：当`a>0`时，开口向上；当`a<0`时，开口向下；- 对称轴：直线`x=h`；- 顶点：坐标为`(h, k)`；- 增减性：当`a>0`时，`x<h`时函数值递减，`x>h`时函数值递增；当`a<0`时，`x<h`时函数值递增，`x>h`时函数值递减。

2.3 二次函数的性质- 顶点式与标准式的转化；- 开口方向、对称轴、顶点坐标之间的关系；- 图像与x轴的交点：解方程`ax^2+bx+c=0`。

2.4 实际问题举例- 利用二次函数解决生活中的最优化问题；- 利用二次函数解决几何问题。

3. 教学过程3.1 导入- 通过实例引入二次函数的概念，引导学生思考二次函数的特点；- 引导学生利用二次函数的一般形式和顶点式进行函数表达。

3.2 新课讲解- 讲解二次函数的图像特征，如开口方向、对称轴等；- 讲解二次函数的性质，如顶点式与标准式的转化等；- 结合实例讲解利用二次函数解决实际问题。

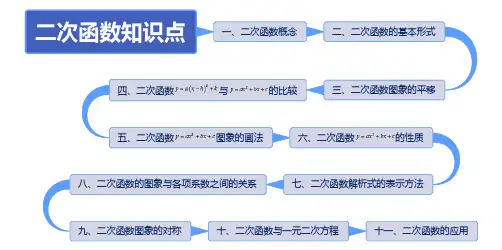
四、二次函数与的比较五、二次函数图象的画法六、二次函数的性质二次函数的结构特征（是常数，）的函数，，而可以为零．二次函数的定的二次式，的是常数，是二次项系数，是一次项系数，是二次函数基本形式：的性质的符号标轴时，随的增大而增大；随的增大而减小；时，有最小值．轴时，随的增大而减小；随的增大而增大；时，有最大值．2. 的性质的符号标轴时，随的增大而增大；随的增大而减小；时，有最小值．轴时，随的增大而减小；随的增大而增大；时，有最大值．3. 的性质的符号时，随的增大而增大；随的增大而减小；时，有最小值．时，随的增大而减小；随的增大而增大；时，有最大值．4.的性质的符号时，随的增大而增大；随的增大而减小；时，有最小值．时，随的增大而减小；随的增大而增大；时，有最大值．，确定其顶点坐标的形状“值正右移，负左移；值正上移，负沿轴平移个单位，变成（或）沿轴平移：向左（右）平移个单变成（或）四、二次函数与的比较从解析式上看，与是两种不同的表达形式，后者通过配方可以得到前者，即，其中．五、二次函数图象的画法五点绘图法：利用配方法将二次函数化为顶点式，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与轴的交点、以及关于对称轴对称的点、与轴的交点，（若与轴没有交画草图时应抓住以下几点：开口方向，对称轴，顶点，与轴的交点，与轴的六、二次函数的性质当时，抛物线开口向上，对称轴为，顶点坐标为当时，随的增大而减小；当时，随的增大而增大；当时，有最小值当时，抛物线开口向下，对称轴为，顶点坐标为．当时，随的增大而增大；当时，随的增大而减小；当时，有最大值一般式：（，，为常数，）顶点式：（，，为常数，）两根式：（，，是抛物线与轴两交点的横坐标）点式，但并非所有的二次函数都可以写成交点式，只有抛物线与轴有交点，即时，抛物线的解析中，时，抛物线开口向上，时，抛物线开口向下，在的前提下时，，即抛物线的对称轴在轴左侧时，，即抛物线的对称轴就是轴时，，即抛物线对称轴在轴的右侧在的前提下，结论刚好与上述相反，即时，，即抛物线的对称轴在轴右侧时，，即抛物线的对称轴就是轴时，，即抛物线对称轴在轴的左侧总结起来，在确定的前提下，决定了抛物线对称轴的位置．ab的符号的判定：对称轴在轴左边则，在轴的右侧则，概括的说就是当时，抛物线与当时，抛物线与当时，抛物线与轴的两个交点的横坐标，一般选用两根式关于轴对称后，得到的解析式是关于轴对称后，得到的解析式是关于轴对称后，得到的解析式是关于轴对称后，得到的解析式是关于原点对称后，得到的解析式是关于原点对称后，得到的解析式是关于顶点对称后，得到的解析式是关于顶点对称后，得到的解析式是关于点(m,n)系（二次函数与轴交点情况）一元二次方程是二次函数当函数值时的特殊图象与轴的交点个数时，图象与轴交于两点是一元二次方程的两根．这两点间的.时，图象与轴只有一个交点时，图象与轴没有交点时，图象落在轴的上方，无论为任何实数，都有时，图象落在轴的下方，无论为任何实数，都有抛物线的图象与轴一定相交，交点坐标为，⑴ 求二次函数的图象与轴的交点坐标，需转化为一元二次方程⑵ 求二次函数的最大（小）值需要利用配方法将二次函数由一般式转化为顶点式⑶ 根据图象的位置判断二次函数中，，的符号，或由二次函数中，，的符号判断图象的位置，要数形结合⑷ 二次函数的图象关于对称轴对称，可利用这一性质，求和已知一点对称的点坐标，或已知与轴的一个交点坐标，可由对称性求出另一个交点坐标⑸ 与二次函数有关的还有二次三项式，二次三项式本身就是所含字母的二次函数；下面以时为例，揭示二次函数、二次三项式和一元二次方程之间的内在联系。