10二次函数思维导图

二次函数知识点总结图高三高三学习阶段，数学中的二次函数知识是必不可少的。

本文将对二次函数的相关知识进行总结和图解，帮助高三学生更好地理解和掌握这一知识点。

一、基本概念二次函数是数学中一个重要的函数类型，其一般形式为f(x) =ax^2 + bx + c，其中a、b、c为常数，且a ≠ 0。

该函数的图像通常为一个开口向上或向下的抛物线，具有以下特征：对称轴、顶点、判别式、零点等。

1. 对称轴二次函数的对称轴是垂直于x轴的一条直线，过抛物线的顶点，由x = -b/2a确定。

2. 顶点二次函数的顶点是抛物线的最高点（a>0，开口向上）或最低点（a<0，开口向下），由坐标(-b/2a, f(-b/2a))确定。

3. 判别式二次函数的判别式D = b^2 - 4ac，用来判断函数的图像与x轴的交点情况：- 当D > 0时，函数与x轴有两个不同的交点，即抛物线与x轴交于两个不同的实数解；- 当D = 0时，函数与x轴有一个交点，即抛物线与x轴交于一个重根（重复解）；- 当D < 0时，函数与x轴没有交点，即抛物线与x轴不相交。

4. 零点二次函数的零点是函数与x轴相交的点，即方程ax^2 + bx + c = 0的解。

二、图像特征与性质了解二次函数的图像特征和性质，可以更好地分析问题和解决实际应用题。

1. 开口方向二次函数的开口方向由a的正负决定，当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

2. 最值二次函数的最值即为顶点的纵坐标，当a>0时，函数的最小值为f(-b/2a)；当a<0时，函数的最大值为f(-b/2a)。

3. 函数值对于给定的x值，可以通过函数的表达式计算得到相应的y值。

当x在对称轴两侧时，函数值相等。

4. 对称性二次函数具有对称性，以对称轴为轴线，左右两侧的图像是关于对称轴对称的。

三、常见问题分析学好二次函数的知识，需要能够灵活运用，解决与实际问题相关的应用题。

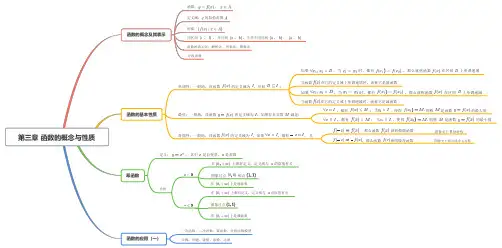
函数：，
定义域：的取值范围
函数的概念及其表示
值域：
闭区间，，开区间，，半开半闭区间，，，
函数的表示法：解析法、列表法、图象法分段函数
如果，当时，都有，那么就称函数在区间上单调递增
单调性：一般地，设函数的定义域为，区间：
当函数
在它的定义域上单调递增时，就称它是增函数
如果
，当时，都有，那么就称函数在区间上单调递减
当函数
在它的定义域上单调递减时，就称它是减函数
函数的基本性质
最值：一般地，设函数的定义域为，如果存在实数满足：
，都有
；
，使得
则称
是函数
的最大值
，都有；
，使得
则称是函数
的最小值
第三章函数的概念与性质
奇偶性：一般地，设函数的定义域为，如果，都有，且
，那么函数
就叫做偶函数图象关于
轴对称
，那么函数
就叫做奇函数
图象关于原点成中心对称
定义：
，其中是自变量，是常数
在
上都有定义，定义域与
的取值有关
幂函数
图象过点
和点
性质
在上是增函数
在上都有定义，定义域与
的取值有关
图象过点
在
上是减函数
函数的应用（一）
一次函数、二次函数、幂函数、分段函数模型
步骤：审题、建模、求模、还原。

九上数学二次函数思维导图二次函数是九年级学数学的一个重要知识点，对于这个知识点的学习，我们可以通过一些思维导图来进行。

下面小编精心整理了九上数学二次函数思维导图，供大家参考，希望你们喜欢!九上数学二次函数思维导图欣赏九上数学二次函数：对称关系对于一般式：①y=ax2+bx+c与y=ax2-bx+c两图像关于y轴对称②y=ax2+bx+c与y=-ax2-bx-c两图像关于x轴对称③y=ax2+bx+c与y=-ax2+bx+c-b2/2a关于顶点对称④y=ax2+bx+c与y=-ax2+bx-c关于原点中心对称。

(即绕原点旋转180度后得到的图形)对于顶点式：①y=a(x-h)2+k与y=a(x+h)2+k两图像关于y轴对称，即顶点(h, k)和(-h, k)关于y轴对称，横坐标相反、纵坐标相同。

②y=a(x-h)2+k与y=-a(x-h)2-k两图像关于x轴对称，即顶点(h, k)和(h, -k)关于x轴对称，横坐标相同、纵坐标相反。

③y=a(x-h)2+k与y=-a(x-h)2+k关于顶点对称，即顶点(h, k)和(h, k)相同，开口方向相反。

④y=a(x-h)2+k与y=-a(x+h)2-k关于原点对称，即顶点(h, k)和(-h, -k)关于原点对称，横坐标、纵坐标都相反。

(其实①③④就是对f(x)来说f(-x),-f(x),-f(-x)的情况)九上数学二次函数：位置决定因素一次项系数b和二次项系数a共同决定对称轴的位置。

当a>0,与b同号时(即ab>0)，对称轴在y轴左; 因为对称轴在左边则对称轴小于0，也就是- b/2a<0,所以b/2a要大于0，所以a、b 要同号当a>0,与b异号时(即ab<0)，对称轴在y轴右。

因为对称轴在右边则对称轴要大于0，也就是- b/2a>0, 所以b/2a要小于0，所以a、b要异号可简单记忆为左同右异，即当对称轴在y轴左时，a与b同号(即a>0，b>0或a<0，b<0);当对称轴在y轴右时，a与b异号(即a0或a>0，b<0)(ab<0)。

九年级上册数学二次函数思维导图对于九年级上册数学的二次函数，运用图形更容易掌握。

下面小编精心整理了九年级上册数学二次函数思维导图，供大家参考，希望你们喜欢!九年级上册数学二次函数思维导图欣赏九年级上册数学二次函数：顶点式y=a(x-h)²+k(a≠0,a、h、k为常数),顶点坐标为(h,k) ，对称轴为直线x=h，顶点的位置特征和图像的开口方向与函数y=ax²的图像相同，当x=h时，y最大(小)值=k。

有时题目会指出让你用配方法把一般式化成顶点式。

例：已知二次函数y的顶点(1,2)和另一任意点(3,10)，求y的解析式。

解：设y=a(x-1)²+2，把(3,10)代入上式，解得y=2(x-1)²+2。

注意：与点在平面直角坐标系中的平移不同，二次函数平移后的顶点式中，h>0时，h越大，图像的对称轴离y轴越远，且在x轴正方向上，不能因h前是负号就简单地认为是向左平移。

具体可分为下面几种情况：当h>0时，y=a(x-h)²的图像可由抛物线y=ax²向右平行移动h个单位得到;当h<0时，y=a(x-h)²的图像可由抛物线y=ax²向左平行移动|h|个单位得到;当h>0,k>0时，将抛物线y=ax²向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)²+k的图象;当h>0,k<0时，将抛物线y=ax²向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)²+k的图象;当h<0,k>0时，将抛物线y=ax²向左平行移动|h|个单位，再向上移动k个单位可得到y=a(x-h)²+k的图象;当h<0,k<0时，将抛物线y=ax²向左平行移动|h|个单位，再向下移动|k|个单位可得到y=a(x-h)²+k的图象。

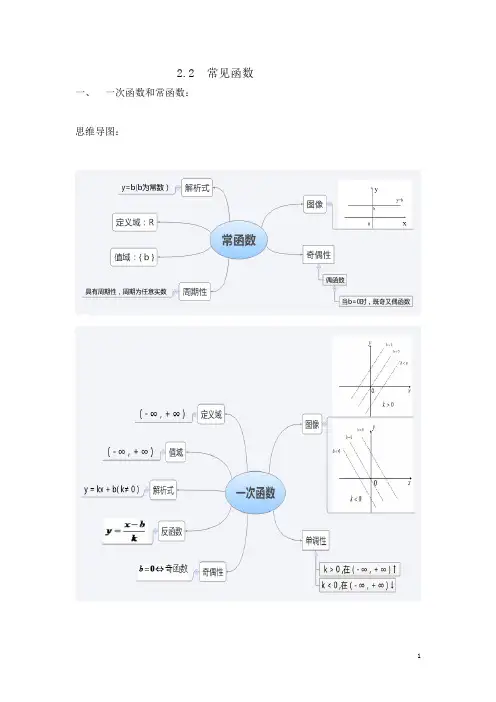
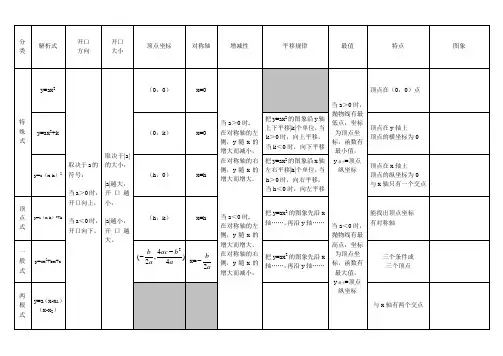
2.2常见函数一、一次函数和常函数：思维导图：（一） 、一次函数 〔二〕、常函数 定义域：〔- ∞，+ ∞〕 定义域: 〔- ∞，+ ∞〕 值 域：〔- ∞，+ ∞〕 正 k=0 反 值 域：{ b }解析式：y = kx + b ( k ≠ 0 ) 解析式：y = b ( b 为常数)图 像：一条与x 轴、y 轴相交的直线 图 像：一条与x 轴平行或重合的直线b>0 b=0 b<0 K > 0 k < 0单调性： k > 0 ,在〔- ∞，+ ∞〕↑ 单调性：在〔- ∞，+ ∞〕上不单调 k < 0 ,在〔- ∞，+ ∞〕↓奇偶性：奇函数⇔=0b 奇偶性: 偶函数 非奇非偶⇔≠0b周期性: 非周期函数 周期性：周期函数，周期为任意非零实数 反函数：在〔- ∞，+ ∞〕上有反函数 反函数:在〔- ∞，+ ∞〕上没有反函数 反函数仍是一次函数例题：二、二次函数1、定义域：〔- ∞，+ ∞〕2、值 域： ),44[,02+∞-∈>ab ac y a]44,(,02ab ac y a --∞∈<3、解析式：)0(2≠++=a c bx ax y4、图 像:一条开口向上或向下的抛物线 开口向下，开口向上；正负：增大，开口缩小绝对值：随着,00<>a a a a正半轴相交与负半轴相交与y c y c c,0,0><对称轴：ab x 2-=对称轴： ；)44,2(2ab ac ab --顶点： 轴交点个数图像与x ac b →-=∆42：与x 轴交点的个数。

两个交点,0>∆一个交点,0=∆无交点,0<∆5、单调性：↑+∞-↓--∞>),2[]2,(,0ab ab a↓+∞-↑--∞<),2[]2,(,0ab ab a6、奇偶性：偶函数⇔=0b7、周期性：非周期函数8、反函数：在〔- ∞，+ ∞〕上无反函数，上及其子集上有反函数或在),2[]2,(+∞---∞ab ab例题:三、反比例函数和重要的分式函数〔一〕、反比例函数 〔二〕、分式函数bax dcx y ++= 定义域：〔- ∞，0〕∪〔0，+ ∞〕 定义域：),(),(+∞---∞aba b 值 域：〔- ∞，0〕∪〔0，+ ∞〕 值 域: ),(),(+∞-∞a c a c解析式：)0()(≠=k xk x f 解析式：)(a bx b ax d cx y -≠++=图 像：以x 轴、y 轴为渐进线的双曲线 图 像：以abx -=和a c y =为渐近线的双曲线y y0 x 0 xk > 0 k < 0单调性： k>0,〔- ∞，0〕↓,〔0，+ ∞〕↓ 单调性:在),(a b --∞和),(+∞-ab上 k<0,〔- ∞，0〕↑,〔0，+ ∞〕↑ 单调性相同 奇偶性：奇函数 奇偶性：非奇非偶 对称性：关于原点对称 对称性：关于点),(aca b -成中心对称 周期性：非周期函数 周期性：非周期函数反函数：在定义域上有反函数， 反函数：在定义域有反函数， 反函数是其本身。

数学第二单元思维导图是一种图形化的工具，可以帮助学生更好地理解和掌握数学的概念。

它的基本结构是由中心主题和周围的子主题构成的。

中心主题代表数学第二单元的核心概念，而周围的子主题则是对中心主题的具体解释和拓展。

一个典型的数学第二单元思维导图会包括以下内容：
- 中心主题：数学第二单元的核心概念。

- 周围的子主题：
- 一次函数：概念、性质、图像、应用。

- 二次函数：概念、性质、图像、应用。

- 平面直角坐标系：概念、性质、图像、应用。

- 几何图形：圆、椭圆、抛物线、双曲线、超几何图形。

使用数学第二单元思维导图的优点是能够让学生更快地理解数学概念，更好地记忆和应用这些概念。

这种图形化的工具可以帮助学生将概念之间的联系视为一个整体，从而更好地理解数学知识。

另外，数学第二单元思维导图还可以帮助学生发掘隐藏在数学概念之间的联系，从而从而更好地理解数学知识。

此外，数学第二单元思维导图还可以帮助学生更好地复习和梳理所学知识，提高学习效率。

学生可以在自己的思维导图中加入自己的理解和解题方法，从而使自己对所学知识有更深刻的理解。

在使用数学第二单元思维导图时，学生应注意以下几点：
- 要尽量使用简单明了的语言表达概念，避免使用生僻的术语。

- 要尽量使用图形或者简单的例子来帮助理解概念，而不是仅仅局限于文字表述。

- 要注意排版，使得思维导图看起来简洁整洁，易于阅读。

数学第二单元思维导图是一种有效的学习工具，能够帮助学生更好地理解和掌握数学的概念，提高学习效率。

(本文部分内容搜集自网络，仅供参考)。

九上数学二次函数思维导图欣赏九上二次函数：对称关系对于一般式：①y=a某2+b某+c与y=a某2-b某+c两图像关于y轴对称②y=a某2+b某+c与y=-a某2-b某-c两图像关于某轴对称③y=a某2+b某+c与y=-a某2+b某+c-b2/2a关于顶点对称④y=a某2+b某+c与y=-a某2+b某-c关于原点中心对称。

(即绕原点旋转180度后得到的图形)对于顶点式：①y=a(某-h)2+k与y=a(某+h)2+k两图像关于y轴对称，即顶点(h,k)和(-h,k)关于y轴对称，横坐标相反、纵坐标相同。

②y=a(某-h)2+k与y=-a(某-h)2-k两图像关于某轴对称，即顶点(h,k)和(h,-k)关于某轴对称，横坐标相同、纵坐标相反。

③y=a(某-h)2+k与y=-a(某-h)2+k关于顶点对称，即顶点(h,k)和(h,k)相同，开口方向相反。

④y=a(某-h)2+k与y=-a(某+h)2-k关于原点对称，即顶点(h,k)和(-h,-k)关于原点对称，横坐标、纵坐标都相反。

(其实①③④就是对f(某)来说f(-某),-f(某),-f(-某)的情况)九上数学二次函数：位置决定因素一次项系数b和二次项系数a共同决定对称轴的位置。

当a0,与b同号时(即ab0)，对称轴在y轴左;因为对称轴在左边则对称轴小于0，也就是-b/2a0,所以b/2a要大于0，所以a、b要同号当a0,与b异号时(即ab0)，对称轴在y轴右。

因为对称轴在右边则对称轴要大于0，也就是-b/2a0,所以b/2a要小于0，所以a、b要异号可简单记忆为左同右异，即当对称轴在y轴左时，a与b同号(即a0，b0或a0，b0);当对称轴在y轴右时，a与b异号(即a0或a0，b0)(ab0)。

事实上，b有其自身的几何意义：二次函数图象与y轴的交点处的该二次函数图像切线的函数解析式(一次函数)的斜率k的值。

可通过对二次函数求导得到。