下载文档原格式
土壤侵蚀的估算方法数据处理流程作者：***时间：2011年10月11日北京天合数维科技有限公司目录（CONTENT）一、所需数据与参数 (3)1、所需数据 (3)2、所需中间参数 (3)2.1、水土保持因子P (3)2.2、地标覆盖因子C (3)2.3、地形因子LS (4)2.4、土壤可视性因子K (4)2.5、降水侵蚀因子R (4)3、所需参数 (5)3.1、潜在土壤侵蚀量Ap (5)3.2、现实土壤侵蚀量Ar (5)3.3、土壤保持量Ac (5)4、指标结果参数 (5)4.1、保护土壤肥力的经济效益Ef (6)4.2、减少土地废弃的经济效益Es (6)4.3、减轻泥沙淤积的经济效益En (6)二、处理流程 (7)1、DEM数据的处理 (8)1.1、坡长L (8)1.2、百分比坡度a (8)1.3、地形因子LS (9)2、气象数据 (9)2.1、月降雨量Pi的计算 (9)2.2、土壤侵蚀力指标R (10)3、土壤类型数据 (10)4、遥感影像数据 (10)5、土壤理性化数据 (11)三、所需参数的计算 (11)四、指标结果参数计算 (11)一、所需数据与参数在计算的过程中，总共涉及到的数据有地形数据、遥感影像数据、气象数据、土壤类型数据、土壤理性化数据以及统计数据，涉及到的中间参数有水土保持因子P，地标覆盖因子C，地形因子LS，土壤可视性因子K，降水侵蚀因子R，所需要的参数有潜在土壤侵蚀量Ap，现实土壤侵蚀量Ar，土壤保持量Ac，指标结果参数有保护土壤肥力的经济效益Ef，减少土地废弃的经济效益Es，减轻泥沙淤积的经济效益En。
1、所需数据在进行土壤侵蚀的估算过程中，需要以下数据：A、地形数据；B、遥感影像数据；C、气象数据，主要是降雨量数据；D、土壤类型数据；E、土壤理性化数据；F、统计数据。
2、所需中间参数在数据处理的过程中，所涉及到的中间参数与计算公式如下。
2.1、水土保持因子P按照游松财的方法，水田的P值取0.15，其他土地利用方式基本没有采取水土保持措施，因此取值为1.00。
实习一一、实习名称地层剥蚀量的估算二、实习原理声波时差法估算剥蚀量：大量实验结果表明，在具有均匀分布的小孔隙的固结地层中，声波传播时间与孔隙度存在正比例线性关系。
因而，不同深度的声波传播时间与不同深度的孔隙度变化可以相类比，即在正常压实情况下可以用指数函数形式来表达声波时差与深度的关系：T=T0exp(-bx)。
其中：Ｘ表示深度；Ｔ表示声波传播时间；Ｔ0为声波在地表的传播时间(Ｘ=0)；ｂ为指数衰变常数。
声波的地表传播时间范围大约为180-210us/ft（591-689us/m），等于纯净水的传播时间（Magara 1976）。
泥浆水混合物的声波时差约为620μｓ/ｍ，此值作为地层最初沉积时的声波时差。
在有剥蚀的情况下现在地表位置与所推算出的古地表位置之间的差值就是所估算的剥蚀量。
密度差法估算剥蚀量：这一方法的理论基础是物质平衡原则。
用数学公式表达为:H=2△ρab/ ρ′a(z)+ ρ′b(z)。
△ρab为上下相邻地层在不整合面接触点上的密度差；ρ′a(z)+ ρ′b(z) 为上覆层(a)和下伏层(b)密度函数在不整合面接触点处的一阶导数；H 为下伏地层被剥蚀的厚度。
三、实习步骤声波时差法估算剥蚀量1、找出被剥蚀地层K1m的顶底深度；2、根据顶底深度范围，挑出在其范围内的声波时差值；3、根据被剥蚀地层内的泥岩层范围，挑出相应范围内的声波时差；4、在挑出的被剥蚀地层泥岩深度值与所对应的声波时差值中，让每个深度值都减去255，得到新的泥岩深度值与其相对应的声波时差值；5、对新得到的泥岩深度值与其相对应的声波时差值做指数公式拟合，分别得到SXS-3井的拟合公式为：y = 389.27*e-0.0005x；SXS-4井的拟合公式为：y = 400.24*e-0.0005x；SXS-5井的拟合公式为：y = 360.57*e-0.0005x；6、把地层最初沉积时的声波时差值620代入所拟合的各井声波时差与深度公式y中，就得到各井的相应深度值x，即剥蚀量值。
收稿日期:2001-03-06第一作者简介:尚可耘,男,1974年生,同济大学海洋地质硕士研究生。
3国家自然科学基金(批准号:49876013)、教育部资助优秀年轻教师基金计划联合资助项目利用声波测井数据估算西湖凹陷地层剥蚀量3尚可耘1 贾健谊2 周祖翼1 梁连喜2(11同济大学海洋地质与地球物理系 上海 200092;21中石化新星石油公司上海海洋石油局 上海 200120) 摘 要 声波测井数据揭示岩层声波时差的规律性的变化,根据这种规律性的变化可以定量求解地层曾经经历过的抬升剥蚀。
作者对声波时差、利用声波测井数据求取地层剥蚀厚度的基本原理及计算方法作了简要介绍,并以东海西湖凹陷3口钻井的实测声波测井数据为例,对这一方法的适用性进行了探讨。
关键词 西湖凹陷 声波测井 ITT 反转构造 剥蚀量 中图分类号:P63118+14 文献标识码:A 文章编号:1008-2336(2001)03-0012-041 前言 反转构造指的是沉积盆地或造山带中构造状态从拉张向挤压的转换,这种转换导致张性盆地(构造)被挤压成为构造高地。
反转构造的识别及其几何学、运动学及动力学的研究已成为含油气盆地构造分析的一个重要组成部分。
由于反转构造会改变沉积盆地的埋藏历史、断层的圈闭性质、流体的运动方向,在盆地深部形成一系列复杂的构造,从而相应地使油气的运移、聚集复杂化,因此,反转构造的研究也已成为当今油气评价的一个主要内容之一。
90年代以来,由于一系列分析技术(包括地震解释、高分辩率生物地层学、裂变径迹、镜质反射率测定等)和模拟技术(沙箱实验模拟和计算机模拟)的日趋完善,使得反转构造的识别及定量研究成为可能(Bally ,1984;Harding ,1985;Cooper et al.,1993;Mitra ,1993;Coward ,1994;周祖翼,1994)。
西湖凹陷是东海陆架中最具油气潜力、规模最大的一个盆地。
自1993年起,在一些国内外学术会议和国内期刊上,出现了有关西湖凹陷发现反转构造的报道(王国纯,1995;陶瑞明,1995),但现有的研究对这些反转构造的几何学特征研究不够深入,对其运动学特征几乎没有涉及,而对其动力学形成机制则多属主观推测,分歧较大。
剥蚀地层厚度模型不论什么样的模型假设和程序，地层剖面中的不整合面破坏任何有规律的孔隙度-深度关系模型，所以在有沉积间断和地层遭剥蚀的情况下，回剥过程中应考虑被剥蚀地层的厚度值，从而将不整合面之下的地层恢复到地史时期的最大埋深，目前关于地层剥蚀量的计算，所用的方法较多，主要有以下几种：（1）地质对比法这是传统的地质法，即将遭剥蚀地区的地层与邻近地区相对剥蚀较少的地层对比，估计被剥蚀地层的厚度。
图示，背斜处剥蚀量最大，往翼部减小，至向斜处减至最小。
通过恢复剥蚀前原始构造剖面，并考虑厚度变化，可求得被剥蚀地层的厚度。
（2）声波时差（或孔隙度）外推作图法利用声波时差（或孔隙度）外推作图估计剥蚀厚度。
图4-示，在已知研究区古湖盆沉积物（C、B和A层）沉积后地表声波时差（或地表孔隙度φo）的条件下，将井实测的ΔtC、ΔtB、ΔtA（换算成φC、φB和φA）的正常趋势线从C、B和A层顶面向上延伸到相应各层沉积后地表Δto（或φo）处，则古湖盆的原始地表（Δto或φo）处的水平线至现在C、B和A层剥蚀面之间的地层厚度（Eco和Ebo）即代表该井C和B层被剥蚀的地层厚度。
声波时差（孔隙度）外推法恢复地层剥蚀厚度原理示意图（据庞雄奇等，1991）（3）沉积速率法剥蚀厚度和剥蚀开始时间的求取可以采用Guidish，T. M. 等（1964）的沉积速率法。
一个古剥蚀面代表着一段时限，在这个时限内有某一厚度的沉积被剥蚀了，于是这段时限实际包括了两部分：一部分是该厚度的沉积岩沉积时所用的时间，另一部分是该厚度的沉积岩被剥蚀所用的时间，如果知道被剥蚀岩层的沉积速度和不整合面上下岩层的绝对年龄，就可以计算出被剥蚀掉的沉积层厚度。
在计算时还需要作出关于剥蚀速率的判别，即剥蚀速率是等于不整合面以下岩层的沉积速率，还是不整合面以上岩层的沉积速率。
a图表示有沉积间断，其间并无剥蚀发生，取界面上下沉积岩的绝对年龄差即可算出其沉积间断的时限。
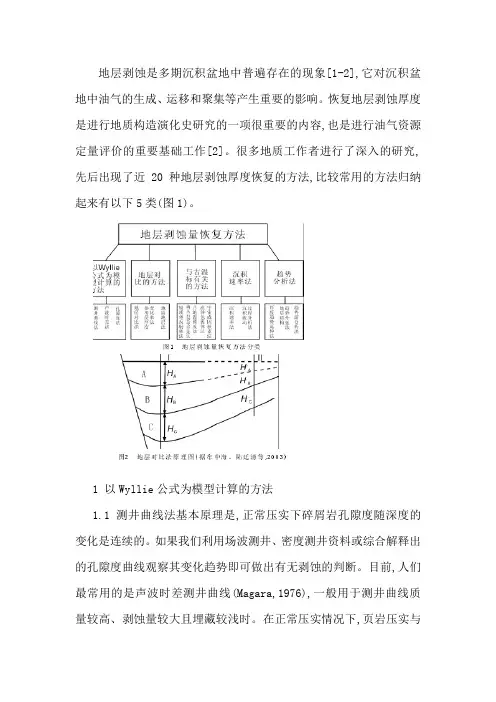
地层剥蚀是多期沉积盆地中普遍存在的现象[1-2],它对沉积盆地中油气的生成、运移和聚集等产生重要的影响。
恢复地层剥蚀厚度是进行地质构造演化史研究的一项很重要的内容,也是进行油气资源定量评价的重要基础工作[2]。
很多地质工作者进行了深入的研究,先后出现了近20种地层剥蚀厚度恢复的方法,比较常用的方法归纳起来有以下5类(图1)。
1 以Wyllie公式为模型计算的方法1.1 测井曲线法基本原理是,正常压实下碎屑岩孔隙度随深度的变化是连续的。
如果我们利用场波测井、密度测井资料或综合解释出的孔隙度曲线观察其变化趋势即可做出有无剥蚀的判断。
目前,人们最常用的是声波时差测井曲线(Magara,1976),一般用于测井曲线质量较高、剥蚀量较大且埋藏较浅时。
在正常压实情况下,页岩压实与上覆的负荷或埋深有关,孔隙度是页岩压实程度的度量,而声波测井资料直接反映了页岩压实程度的大小。
因此,根据正常的压实趋势,应用声波测井资料推算沉积层的压实程度,就可以估算被剥蚀地层的厚度。
它的应用依赖于正确确定地下沉积层的孔隙度-深度和声波传播时间-深度关系。
该方法的缺点是,当剥蚀面再度下沉至大于剥蚀厚度的深度以下时,因压实趋势改变,则无法计算出剥蚀量的大小。
2 地层对比的方法2.1 地层对比法地层对比法是比较传统的恢复剥蚀厚度的方法,即将要恢复剥蚀厚度的地层与邻区未被剥蚀的相同地层进行对比,求出其沉积厚度,除去该地层的残余厚度即可得到地层剥蚀量。
运用地层对比法求剥蚀厚度的原理如图2所示,图中Ⅰ,Ⅱ分别代表地层的深凹处(假设没有剥蚀的地层)和斜坡处(假设有剥蚀的地层)的钻井位,以C组地层为参考地层,即假设C地层在斜坡处没有剥蚀,则深凹处的地层厚度比为:λA=HA/HC其中,HA,HC分别为A地层和C地层在深凹处的厚度。
由地层对比法的原理可以计算斜坡处A地层在斜坡处的剥蚀厚度ΔHA:ΔHA=λA×HC’-HA’其中,HA’、HC’分别为A地层和C地层在斜坡处的厚度。
专利名称：地层剥蚀量计算方法专利类型：发明专利
发明人：李弘,林正良,吕慧,朱克申请号：CN201510290869.9申请日：20150530
公开号：CN106291695A
公开日：
20170104
专利内容由知识产权出版社提供
摘要：本发明提供一种地层剥蚀量计算方法，该方法包括：根据测井数据和地震数据标定井震时深，确定待计算区域地震层位；确定待计算区域的剥蚀地层界面及下伏完整地层的顶底界面；根据相邻层厚度比值及下伏层厚度计算上覆层沉积厚度；以及若计算值大于所述上覆层的残余层厚度，则超出部分为剥蚀厚度。
通过上述技术方案，结合使用地震数据和测井数据，根据地质沉积规律利用相邻层厚度比值计算地层剥蚀量，计算结果可靠、井间连续性强。
申请人：中国石油化工股份有限公司,中国石油化工股份有限公司石油物探技术研究院
地址：100728 北京市朝阳区朝阳门北大街22号
国籍：CN
代理机构：北京思创毕升专利事务所
代理人：刘明华
更多信息请下载全文后查看。
计算地层剥蚀量方法恢复地层剥蚀厚度是研究盆地演化史和进行油气资源定量评价的重要基础工作，通过地层剥蚀量的计算、地层最大埋深的确定，可以帮助我们确定烃源岩生油期、生气期，进而准确评价油气资源潜力，优选勘探目标。
目前存在多种计算地层剥蚀量的方法，如：（1）地层对比法、（2）沉积速度法（Van Hinte,1978）、（3）声波测井曲线法（Magara,1976）、（4）镜质体反射率（R o）法（Dow,1977）、（5）地震地层学法（尹天放等，1992）、（6）最优化方法（郝石生等，1988）、（7）天然气平衡浓度法（李明诚等，1996）等。
一、构造横剖面法该方法通过对构造发育特征的分析，推测地层的剥蚀量，基本原理如图1所示。
该方法适用于构造发育特征比较明显、尤其是角度不整合地区，对平行不整合的剥蚀量计算受到一定的限制。
图1 构造横剖面法推算地层剥蚀量示意图可以根据残余地层的展布特征及构造运动的特点推算出剥蚀厚度。
以某三维地震剖面为例，通过该方法可估算出该地区印支运动对C－P顶面造成的剥蚀量的剥蚀量最大可到1500m左右。
最大不超过1000m，J3～K沉积时期，J1＋2二、沉积速率法该方法是依据不整合面上下地层的沉积速率及绝对年龄计算地层剥蚀量，具体可分如图2所示的几种情形进行处理（Guidish等，1985）：图2 对不整合面的不同处理方法（Guidish等，1985）（a）将不整合面视为沉积间断，期间无剥蚀发生，界面上下沉积岩的绝对年龄的差值即为沉积间断的时间。
（b）发生了剥蚀，视剥蚀掉的地层的沉积速率等于其剥蚀速率，所以：H e=[(V上＋V下)/2]×[(T下－T上)/2]（c）认为剥蚀掉的地层的沉积速率等于不整合面之下地层的沉积速率，而其剥蚀速率等于不整合面之上的地层的沉积速率，因此剥蚀开始的时间（T e）和剥蚀厚度（H e）即为：T e=（V上T上＋V下T下）/（V上＋V下）H e=V上（T e－T上）该方法必须在知道不整合面上下地层的沉积速率及绝对年龄的情况下才能适用。
三、声波时差法沉积物在沉积、埋藏过程中，孔隙度随埋深的增大呈指数减小，又因为在具有均匀分布的小孔隙的固结地层中，孔隙度与传播时间之间存在着正比例线性关系（Wyllie等，1956），因而在Magara K.（1976）总结了Athy（1930）、Rubey 和Hubbert（1959）等前人的研究成果，提出了泥页岩在正常压实情况下的声波时差－深度关系式（Magara K.，1976）：Δt=Δt0e-CH式中，Δt：泥页岩在深度H处的传播时间(μs/m)Δt0：外推至地表的传播时间(μs/m)C：正常压实趋势斜率(m-1)H：埋深（m）如果地层为连续沉积，则泥页岩声波时差与深度满足上述关系式，在半对数坐标系中为线性相关；如果某一地区经历了抬升和剥蚀，那么泥页岩声波时差与深度的正常压实趋势线与未遭受剥蚀地区的相比，则向纵坐标偏移，即在所有的深度上都向压实程度增强方向偏移，根据这一偏移趋势大小，将其压实趋势线上延到未经历压实的Δt0处，则Δt0与剥蚀面处的高差即为剥蚀厚度。
这一原理与方法是建立在“泥岩沉积物的压实形变为塑性形变，不会发生回弹”这一前提的基础上，而且目前人们普遍认为其只适用于新沉积物厚度必须小于地层剥蚀厚度的情况下，否则原泥岩孔隙度将被改造而失去定量计算地层剥蚀量的可能（张博全，1992）。
然而，孔隙度并不是埋深的函数，除了受埋深直接控制的压力因素外，沉积速率、沉积环境、构造背景等也对压实效应产生重要影响，因此判断能否运用压实曲线资料进行地层剥蚀量的估算的标准不应该是依据剥蚀地层厚度与后沉积的地层厚度的大小比较，而应该是判断剥蚀前地层的压实效应是否被后来的沉积地层所改造。
造成间断面之下的地层压实趋势线未被改造的原因主要有如下三种：1、后来沉积的地层厚度远小于剥蚀厚度，其产生的压实效应不足以对间断面之下的地层进行改造；2、由于上覆地层的底部存在低渗透层的隔档，阻止了上覆地层对下伏地层的压实改造；3、由于间断面上下地层的沉积环境、沉积速率、及改造背景存在明显差异，造成界面上下地层的压实趋势线的斜率不同，而新沉积地层产生的负荷压力还不足以对剥蚀前沉积的地层进行改造。
图3 声波时差法计算地层剥蚀厚度示意图因此，我们只要能确定间断面之下地层的压实效应未被后来沉积物所改造，那么，就能依据其保留下来的剥蚀前的压实趋势线，进行恢复地层剥蚀量的估算。
具体的计算步骤如下：首先分别对间断面上下的声波时差－埋深曲线进行对数回归，得到两个回归方程，取埋藏深度为0（H＝0），依据间断面之上的声波时差－埋深关系回归方程，求算出地表的声波时差值Δt0，而后将Δt0值代入间断面之下的埋深－声波时差回归方程，得到剥蚀前地表相对于现今地表的深度，该深度与间断面现今埋深的差值即为剥蚀厚度。
依据同样的原理，也可用作图法求得地层剥蚀厚度，如图3所示。
四、镜质体反射率（R o）法（Dow，1977）镜质体是高等植物木质素经过生物化学降解、凝胶化作用而形成的凝胶体，在受热过程中，随着温度的上升，其芳构化程度和芳环缩聚程度逐渐增大，且缩合芳环排列的定向性和有序程度增强，这使得镜质体的光学性质发生相应的变化，表现为镜质体反射率逐渐增高，且具有不可逆性。
因此镜质体反射率能记录下有机质所经历的整个受热地质历史中的最大温度信息，在无异常热流（如岩浆体侵入、火山活动等）的正常地质背景下，它主要受温度和有效加热时间的影响，换而言之，它是地温梯度和沉积速率的函数。
对连续沉积的地层而言，镜质体反射率（R o）与埋深（H）呈对数关系，在半对数直角坐标系中为线性相关；如果地层存在间断，H－Log R o的关系图（即成熟度剖面）将不连续，或间断面上下的成熟度剖面曲线的斜率存在差异，因此根据这些特征可以进行地层剥蚀量的恢复和平均古地温的求取。
运用Ro计算地层剥蚀量Dow（1977）最早提出用R o计算地层剥蚀量，具体方法如图4所示。
图中成熟度剖面显示地层剥蚀前的R o记录还没有被新的地温场改造，间断面之上地层中最底部N点的R o％值为0.62，间断面之下地层最顶部M点的R o％值为0.94，其差值0.32只表明由于间断面的发育而造成的N、M点热变质程度目前的差异，因此用0.32恢复的剥蚀厚度远比实际剥蚀厚度小，因为0.94才是较真实地代表了M点最大埋深时的变质程度。
图4 印度尼西亚某井的成熟度剖面及地层剥蚀量估算（引自Dow, 1977）所以更正确的方法是：依据间断面之下地层中保留下来的剥蚀前的成熟度剖面趋势线，将其上延至古地表附近的R o％最小值处（目前人们普遍认为地表附近R o％最小值为0.18～0.20），也就是延至R o％为0.20处，则该点在成熟度剖面中所代表的深度值为剥蚀前古地表相对于现今地表的深度，其与间断面所在深度的差值即为地层剥蚀厚度。
与声波时差法类似，判断能否用镜质体反射率进行剥蚀量的计算是看间断面之下的地层的热史记录是否被改造，如果保留有原来的记录，则可以恢复地层剥蚀量，如果剥蚀前的热史记录被完全改造，R o则不能用于恢复地层剥蚀厚度。
对某一具体的井或剖面而言，如果在不整合面上下所测试的Ro数据点多且连续，能够明显反映出不整合面上下镜质体反射率随埋深变化的趋势差异，则可采用上述方法计算（如图5所示）。
a. b.图5 镜质体反射率对义155、桩11井剥蚀量的计算但在多数情况下，由于受取芯段的限制，只有很少的井自下而上有完整的数据点，大部分的井都只是几个数据点，很难连成一条趋势线，面对这种情况，我们首先通过各井的镜质体反射率与济阳凹陷标准成熟度曲线的对比，确定数据点所曾到达的最大埋深，再依据图6所示的数据点在剥蚀前后的埋深与地层剥蚀量的关系来推算剥蚀量。
图6 地层剥蚀前后数据点A埋深变化示意图注：H1为剥蚀前A点的最大埋深，H2为数据点现今埋深，H3为不整合面的现今埋深，因此剥蚀掉的地层厚度He = H1 —（H2－H3）五、磷灰石裂变径迹法磷灰石裂变径迹分析（Apatite Fission Track Analysis，简称AFTA）是近十几年发展起来的恢复沉积盆地热史的一种新方法。
该方法是建立在磷灰石所含238U自发裂变产生的径迹在地质历史时间内随温度增高而发生退火行为这一化学动力学原理基础之上的。
由于磷灰石在沉积岩中分布十分广泛，其径迹退火带温度与油窗温度基本一致，且对温度十分敏感，不仅可以表示盆地经历的最高古地温，而且可以反映地史时期温度的变化，因此人们常用此方法来研究盆地的沉积史和地层剥蚀量（Green P. F. 等，1989；潘长春等，1989；康铁笙、王世成，1990，1991）。
实验表明，磷灰石中的238U自晶格形成后，便以恒定不变的速度不断地自发裂变，所产生的一对高能裂变碎片沿相反方向运动，穿射矿物晶格从而造成宽度约为10-3μm的辐射创伤，这就是磷灰石裂变径迹。
经过化学蚀刻扩大以及其他技术方法处理，可以在不同光学显微镜下对其进行观察。
人们普遍认为，在地质历史时期诸多物化因素中，只有温度对裂变径迹的稳定性有影响（Fleischer R. L.等，1965，1975；Naeser C. W.,1979）。
裂变径迹因受热而发生衰变，表现为长度缩短，密度减小，人们将这一现象称之为退火。
地质历史时期的退火带温度范围约为65～125o C之间（Geadow A.J.W.等，1983），与油气盆地的生油窗口相当吻合。
目前，国内外学者经过对许多沉积盆地的分析试验，提出了五项能够指示古地温的裂变径迹指标，即：裂变径迹年龄、单晶粒表观年龄随埋深的变化、单晶粒年龄的频率分布、平均径迹长度随埋深的变化和径迹长度的频率分布。
图7 磷灰石五项指标与温度的关系（Green等，1987）Green等人（1987）通过对澳大利亚南部奥特韦裂谷盆地的研究发现，上述五项指标随温度的变化呈现出良好的相关性（图7 ），Laslett等（1987）对Green等（1986）的实验数据进行了统计，提出了径迹退火的扇型模型，Carlson(1990)则从微观角度提出了退火的物理模型，这些模型为定量研究径迹数据、提取热史信息提供了数学基础。
周礼成等（1992）通过对一些已知热史盆地的裂变径迹长度分布的数值模拟，为沉积盆地热史定性分析提供了判断模式。
如正态或似正态分布表示升温过程，或总体上是升温过程，中间有小的降温；负偏分布表示降温冷却过程（也可能中间有小的升温）；双峰分布表示典型的升温－降温－恒低温（或不高的升温）过程。
地层抬升遭受剥蚀的过程是一个降温冷却的过程，因此依据上述规律及原理，可以根据裂变径迹五项指标的变化确定具体的降温幅度，再运用古地温梯度资料求得抬升量和剥蚀厚度。
