第9讲动力学分析和力

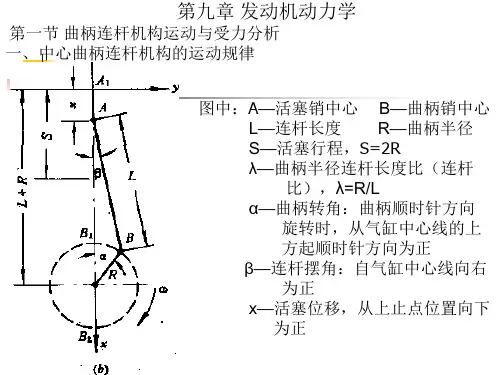
第9章平面连杆机构的动力分析与平衡平面连杆机构是由若干个连杆组成的机械系统，常用于研究机械系统的动力学性质。

对于平面连杆机构的动力分析与平衡，主要是研究其运动学和动力学方程，并进行相应的力和动量平衡计算。

以下将从运动学和动力学两个方面进行详细介绍。

1、运动学分析平面连杆机构的运动学分析是研究机构的位置、速度和加速度的关系。

其中，位置分析主要是根据连杆的几何性质，通过连杆的长度、夹角和初始位置等参数，确定连杆机构的位置关系。

速度分析主要是研究各连杆的线速度和角速度之间的关系，通过运用位移法和速度图解法，可以求解各连杆关节处的速度。

加速度分析主要是研究各连杆的线加速度和角加速度之间的关系，可以通过速度分析的基础上运用动图解法求解。

2、动力学分析平面连杆机构的动力学分析是研究机构中各连杆所受力和动量的关系，进而分析机构的运动特性。

动力学分析主要包括力分析和动量平衡两个方面。

力分析主要是研究在给定外部载荷下，各连杆之间的约束力和连接力，分析力的大小、方向和位置。

动量平衡主要是研究机构质点的动量矩等于零，根据牛顿第二定律和冲量动量定理，可以建立平面连杆机构的运动方程，进而求解各连杆的加速度和力。

平面连杆机构的平衡主要涉及到静平衡和动平衡两个方面。

静平衡要求在机构基准位置时，机构中各连杆和连接处的力矩之和等于零，可以通过力分析和力矩平衡方程求解。

动平衡要求机构中各连杆的质心加速度等于零，在给定外部载荷和给定输入力矩的情况下，可以通过动量平衡方程求解。

总结来说，平面连杆机构的动力分析与平衡需要进行运动学和动力学的分析，通过建立力分析和动量平衡方程，求解各连杆的加速度和力，进而研究机构的运动特性和平衡性。

对于平面连杆机构的动力分析与平衡研究，可以为机械设计和动力学性能优化提供理论依据。

机械工程中的动力学分析引言：机械工程是一门研究机械结构和运动规律的学科，其中动力学分析是机械工程中的重要内容之一。

动力学分析的目的是研究物体在力的作用下的运动规律，通过分析物体的运动状态和力的关系，可以揭示物体的力学特性，并为机械系统的设计和优化提供理论依据。

本教案将从运动学和动力学两个方面，对机械工程中的动力学分析进行深入探讨。

一、运动学分析运动学是研究物体运动状态和运动规律的学科，是动力学分析的基础。

在机械工程中，运动学分析可以通过描述物体的位置、速度和加速度等运动参数来研究物体的运动规律。

1. 位置分析位置是描述物体在空间中的位置信息，可以用坐标系来表示。

在机械工程中，常用的坐标系包括笛卡尔坐标系、极坐标系和柱坐标系等。

通过确定物体在坐标系中的位置，可以揭示物体的运动轨迹和位置变化规律。

2. 速度分析速度是描述物体运动快慢和方向的物理量，可以用矢量来表示。

在机械工程中，速度可以分为线速度和角速度两种。

线速度是物体在直线运动中单位时间内所经过的路程，角速度是物体在旋转运动中单位时间内所转过的角度。

通过分析物体的速度变化，可以了解物体的加速度和运动状态。

3. 加速度分析加速度是描述物体运动变化率的物理量，是速度变化率的导数。

在机械工程中，加速度可以分为线加速度和角加速度两种。

线加速度是物体在直线运动中单位时间内速度的变化量，角加速度是物体在旋转运动中单位时间内角速度的变化量。

通过分析物体的加速度变化，可以了解物体的动力学特性和运动规律。

二、动力学分析动力学是研究物体运动规律和力的作用关系的学科，是机械工程中的核心内容。

在机械工程中，动力学分析可以通过分析物体的运动状态和力的关系，揭示物体的力学特性和运动规律。

1. 牛顿定律牛顿定律是经典力学的基础，描述了物体在力的作用下的运动规律。

根据牛顿定律，物体的运动状态由力的作用决定，力的大小和方向决定了物体的加速度。

通过分析物体所受的力和运动状态，可以计算物体的加速度和运动轨迹。

动力学分析
运动学，从几何的角度（指不涉及物体本身的物理性质和加在物体上的力) 描述和研究物体位置随时间的变化规律的力学分支。

以研究质点和刚体这两个简化模型的运动为基础，并进一步研究变形体(弹性体、流体等) 的运动。

研究后者的运动，须把变形体中微团的刚性位移和应变分开。

点的运动学研究点的运动方程、轨迹、位移、速度、加速度等运动特征，这些都随所选参考系的不同而异；而刚体运动学还要研究刚体本身的转动过程、角速度、角加速度等更复杂些的运动特征。

动力学是理论力学的一个分支学科，它主要研究作用于物体的力与物体运动的关系。

动力学的研究对象是运动速度远小于光速的宏观物体。

动力学是物理学和天文学的基础，也是许多工程学科的基础。

许多数学上的进展也常与解决动力学问题有关，所以数学家对动力学有着浓厚的兴趣。

区别：动力学，即既涉及运动又涉及受力情况的，或者说跟物体质量有关系的问题。

常与牛顿第二定律或动能定理、动量定理等式子中含有m的学问。

含有m说明要研究物体之间的的相互作用（就是力）。

运动学，跟质量与受力无关，只研究速度、加速度、位移、位置、角速度等参量的常以质点为模型的题。

只有一个物体的话研究它的质量没有什么意义，因为质量就是它的惯性大小，或被力影响的强弱，而力必须是两个物体之间的。

第9讲安培力的计算欢迎来到第9讲！在本节课中，我们将学习安培力的计算方法。

安培力是指通过电流在两个导体之间产生的力。

它是一个矢量量，其大小与电流的大小成正比，方向垂直于电流的方向和两个导体之间的距离。

安培力的计算公式如下：F = BIL sin θ其中，F表示安培力的大小，B表示磁感应强度，I表示电流的大小，L表示导体的长度，θ表示电流与磁场方向之间的夹角。

在使用这个公式时，我们需要注意几个要点。

首先，磁感应强度B是由外部磁场决定的，它的大小和方向在给定的环境中是固定的。

其次，电流I是通过导体流动的电荷的总量，单位是安培(A)。

导体的长度L是指电流所通过的导体的长度。

最后，夹角θ是电流方向和磁场方向之间的夹角，它的取值范围是0到180度。

接下来，让我们通过几个例子来学习如何计算安培力。

第一个例子，假设有一根长度为2米的导线，电流大小为5安培，在一个磁感应强度为0.5特斯拉的磁场中。

如果电流方向和磁场方向之间的夹角为30度，我们可以使用安培力的计算公式计算出安培力的大小。

F = (0.5特斯拉) * (5安培) * (2米) * sin(30度) = 2.5牛顿因此，根据给定的条件，这根导线所受的安培力为2.5牛顿。

第二个例子，假设有一根长度为3米的导线，在一个磁感应强度为0.8特斯拉的磁场中，电流大小为10安培。

如果电流方向与磁场方向垂直，即夹角为90度，我们可以使用安培力的计算公式计算出安培力的大小。

F = (0.8特斯拉) * (10安培) * (3米) * sin(90度) = 0牛顿由于sin(90度)等于1，因此该导线所受的安培力为0牛顿。

这是因为电流方向与磁场方向垂直，所以安培力的大小为0。

在实际应用中，安培力的计算常常用于直流电动机、电磁铁等电磁装置的设计和分析中。

通过计算电流通过导体时所受到的安培力，我们可以了解电流对导体的作用，并相应地设计和优化电磁设备。

此外，安培力的计算也有助于我们理解电磁感应、电动力学等领域的物理现象。

详解动力学中力的作用方向的确定方法力是物理学中非常重要的概念，它描述了物体之间相互作用的属性。

在动力学中，力的作用方向对于研究物体的运动和力学性质至关重要。

本文将详解动力学中力的作用方向的确定方法。

一、受力分析法受力分析法是动力学中常用的确定力作用方向的方法之一。

它通过分析物体所受到的各个力的性质来判断力的作用方向。

受力分析法可以分为静态平衡和动态平衡两种情况。

在静态平衡的情况下，物体处于静止状态，所有受力之和为零。

通过观察受力的大小和方向，可以确定力的作用方向。

例如，当一个物体受到重力和支持力作用时，重力向下，支持力向上，力的作用方向可以确定为竖直向上。

在动态平衡的情况下，物体处于匀速直线运动状态，所有受力之和为零。

同样，通过观察受力的大小和方向，我们可以确定力的作用方向。

例如，当一个物体受到摩擦力和推力作用时，摩擦力与推力大小上相等且方向相反，力的作用方向可以确定为与推力方向相反。

二、牛顿第三定律牛顿第三定律指出，任何两个物体之间的相互作用力具有大小相等、方向相反的特性。

根据这个定律，我们可以使用另一个物体所受到的力来确定力的作用方向。

例如，当一个物体在水中游泳，它对水施加一个向后的推力，根据牛顿第三定律，水对物体产生一个向前的作用力，力的作用方向可以确定为向前。

三、实验确定法除了受力分析法和牛顿第三定律，我们还可以通过实验来确定力的作用方向。

实验方法可以更加直观地展示力的作用效果。

通过实验，我们可以利用各种测量工具，如力传感器、弹簧测力计等，来测量物体所受到的力的大小和方向。

例如，在测量弹簧的伸长量时，我们可以根据弹簧的弹性特性和所受到的外力，确定力的作用方向。

实验方法不仅可以帮助我们确定力的作用方向，还可以验证理论分析的结果，提高研究的准确性和可靠性。

综上所述，动力学中力的作用方向的确定方法主要包括受力分析法、牛顿第三定律和实验确定法。

受力分析法通过对物体受力的性质进行分析来判断力的作用方向；牛顿第三定律则利用相互作用力的大小和方向的对称性来确定力的作用方向；实验确定法通过实验测试来测量力的大小和方向，从而确定力的作用方向。

2、单自由度系统的有阻尼受迫振动单自由度系统的受迫振动理论单自由度系统的受迫振动理论（1）振动微分方程kOx②恢复力F e , 方向指向平衡位置O ，大小与偏离平衡位置的距离成正比。

kxF -=e ③黏性阻尼力F d , 方向与速度方向相反，大小与速度大小成正比。

d dd x xF cv ct=-=-物块的运动微分方程为：22d d sin()d d x x m kx c H t t tw =--+方程两边同除以m ，并令：(ω0, 固有角频率) , (δ, 阻尼系数),得到：mk =20w 2c md =2202d d 2sin()d d x x x h t t td w w ++=——有阻尼受迫振动微分方程的标准形式①激振力F , 简谐激振力。

sin()F H t w =H h m =解可以写成：12xx x =+x 1 对应齐次方程的通解; x 2 对应的是特解。

欠阻尼的情况下( δ<ω0)，齐次方程的通解可写为：1e )t x A d q -=+特解可写为：)sin(2e w -=t b x ε表示受迫振动的相位角落后于激振力的相位角2、单自由度系统的有阻尼受迫振动单自由度系统的受迫振动理论将x 2 代入微分方程，得到:220sin()2cos()sin()sin()b t b t b t h t w w e d w w e w w e w --+-+-=将等式右边的h sin(ωt )做一个变换，得到:sin()sin[()]h t h t w w e e =-+cos sin()sin cos()h t h t e w e e w e =-+-代入微分方程，整理得到:)cos(]sin 2[)sin(]cos )([220=--+---e w e w d e w e w w t h b t h b 对任意瞬时t ，上式都必须是恒等式，所以有：cos )(220=--e w w h b 0sin 2=-e w d h b 2222204)(wd w w +-=hb 2202tan w w dwe -=于是，微分方程的通解为：e)sin()tx A b t d q w e -=++-式中，A 和θ为积分常数，由运动的初始条件确定。

理论力学中的动力学分析在理论力学中，动力学是研究物体受力作用下的运动规律和力的作用关系的学科。

它是力学的一个重要分支，与静力学相对应。

动力学分析通过运用物理学理论和数学方法，揭示了物体运动的规律和力的作用方式。

本文将就理论力学中的动力学分析进行探讨。

动力学分析的基本原理在于牛顿运动定律。

牛顿第一定律指出：任何物体都具有惯性，即物体在没有外力作用时将保持静止或作匀速直线运动。

该定律为动力学分析提供了基础。

其次，牛顿第二定律指出：物体的运动状态随受力而改变，物体所受合力等于物体质量乘以加速度。

这一定律在动力学分析中起着至关重要的作用。

最后，牛顿第三定律表明：力的作用总是成对出现，且大小相等、方向相反，这被称为作用-反作用定律。

动力学分析中，必须考虑到这个定律以正确分析物体间的相互作用。

动力学分析主要关注以下几个方面：质点的运动、刚体的运动、动力学方程的建立和解法以及力的分析。

首先，在质点的运动中，动力学分析需要确定质点所受的合力，以及由此产生的加速度和运动规律。

对于匀加速运动、自由落体等常见情况，可以通过简单的公式进行分析；而对于复杂的情况，例如曲线运动或非匀加速运动，则需要运用微积分和矢量分析等数学工具进行求解。

其次，在刚体的运动中，动力学分析需要考虑刚体的平动和转动。

对于平动，需要计算刚体所受的合力和合力矩，以及由此产生的加速度和角加速度。

对于转动，需要考虑刚体的转动惯量和角速度，以及刚体所受的力矩。

然后，在动力学分析中，建立和解动力学方程是至关重要的。

根据牛顿第二定律，通过建立物体所受力的合力和合力矩与物体质量、加速度以及惯性矩之间的关系，可以得到动力学方程。

解动力学方程可以推导出物体的运动规律和力的作用方式，进一步分析物体的运动状态。

最后，在力的分析中，动力学分析需要考虑力的种类、力的大小和方向以及力的作用点。

常见的力包括重力、摩擦力、弹力等。

力的分析可以揭示物体间相互作用的规律，为动力学分析提供了重要的依据。

运动物体的动力学特性与受力分析运动物体的动力学特性是物理学中一个非常重要的概念，它描述了物体运动时所受到的力的作用以及运动的规律。

受力分析是动力学研究的核心，通过对物体所受力的分析，我们可以揭示物体运动的原因和规律。

一、动力学特性动力学特性包括物体的质量、速度、加速度和力的作用。

质量指的是物体所具有的惯性，也是物体对外界力的抵抗能力。

质量越大，物体对力的抵抗能力越强。

速度指的是物体在单位时间内所移动的距离，它是衡量运动物体快慢的指标。

加速度则描述了物体在单位时间内速度的变化率，它可以使物体由静止转为运动或改变运动的方向。

力是动力学的核心概念，它是推动物体运动的原因，也是物体所受到的力的结果。

二、受力分析受力分析是动力学研究的基础，它通过对物体所受力的分析，揭示了物体运动的原因和规律。

常见的力包括重力、摩擦力、弹力等。

重力是地球对物体的吸引力，是物体运动的基本力。

根据万有引力定律，物体之间的引力与它们的质量成正比，与它们的距离的平方成反比。

摩擦力是物体与接触表面之间的力，它分为静摩擦力和动摩擦力。

静摩擦力使物体保持在静止状态，动摩擦力则是使物体运动的阻力。

弹力是弹性物体在形变后恢复原状的力，它是由物体内部分子之间的相互作用所产生的。

在受力分析中，我们一般以图示的方式来表示物体所受力的情况。

力的图示使用箭头表示，箭头的长度表示力的大小，箭头的方向表示力的方向。

通过对力的图示进行合成或分解，我们可以分析各个力之间的相互作用，进而推导出物体运动的规律。

三、牛顿运动定律牛顿运动定律是描述物体运动规律的基本原理，它包括三个定律。

第一定律，也称为惯性定律，指出物体在恒力作用下保持静止或匀速直线运动。

第二定律，也称为力的动态定律，指出力是改变物体运动状态的原因。

力等于质量与加速度的乘积，即F=ma。

第三定律，也称为作用反作用定律，指出任何一种力都存在着作用力和反作用力，并且它们大小相等方向相反。

牛顿运动定律为我们研究物体运动提供了重要的工具和方法。

动力学力的分析与计算常见错误解答与纠正方法动力学力的分析与计算在物理学和工程学中具有重要的应用价值。

然而，由于其复杂性和理论性，常常会伴随着一些常见的错误。

本文将就动力学力的分析与计算中常见的错误进行解答与纠正，帮助读者正确地理解和应用动力学力。

一、错误一：对动力学力的定义理解不准确动力学力是指物体受到作用力而产生的加速度。

错误的定义理解可能导致力的计算错误，进而影响到后续的动力学分析。

正确的定义应该是：动力学力是物体所受到的，改变物体运动状态的力。

解答与纠正方法：要正确理解动力学力的定义，首先要明确力的本质是物体间相互作用的结果。

另外，要注意区分动力学力和静力学力，动力学力会引起物体的加速度变化，而静力学力则不会产生加速度变化。

在分析动力学问题时，需要准确判断动力学力的方向和大小。

二、错误二：不考虑惯性力的影响在动力学分析中，常常会遇到惯性力的影响。

惯性力是由于参考系的选择而产生的，如果不考虑惯性力，将导致力的计算错误。

解答与纠正方法：在进行动力学力的分析与计算时，要根据所选取的参考系考虑惯性力的影响。

惯性力的计算可以通过运用惯性力公式进行推导和求解。

在实际应用中，要根据具体情况判断是否需要考虑惯性力，合理选择合适的参考系。

三、错误三：未考虑旋转惯量的影响在分析旋转运动时，常常会遇到旋转惯量的影响。

旋转惯量是物体对旋转运动的惯性度量，未考虑旋转惯量将导致力矩的计算错误。

解答与纠正方法：在进行旋转运动的力学分析时，要考虑物体的旋转惯量。

旋转惯量的计算可以通过物体的形状和质量分布进行推导和求解。

在实际应用中，要根据具体情况合理选择旋转惯量的计算方法，并结合力矩公式进行力矩的计算。

四、错误四：力的叠加原理的误用在动力学力的分析与计算中，常常需要将多个力作用于一个物体进行叠加。

然而，错误地使用力的叠加原理将导致力的计算错误。

解答与纠正方法：在使用力的叠加原理时，要明确各个力的作用位置和方向。

正确的叠加原理应该是：分别计算各个力在物体上产生的力矩，然后将各个力矩相加，最后根据力矩和力臂的关系求解合力的大小和方向。

动力学解析受力分析和质点运动的关系动力学是力学的一个分支，研究物体运动时受到的力的作用及其对物体运动的影响。

在动力学中，对于受到多个力作用的物体，我们可以利用受力分析来解析这些力的合力以及物体的运动情况。

本文将探讨动力学解析受力分析和质点运动的关系。

一、受力分析和受力平衡受力分析是动力学解析的第一步。

在分析受力时，我们需要考虑物体受到的各个方向上的力以及力的大小和方向。

根据牛顿第一定律，当物体受到的合力为零时，物体将保持静止或匀速直线运动，处于受力平衡状态。

当物体受到的合力不为零时，物体将产生加速度，发生非静止的运动。

二、质点运动和牛顿第二定律牛顿第二定律给出了物体受力与加速度之间的关系。

根据牛顿第二定律，物体的加速度与受到的合力成正比，与质量成反比。

即F = ma，其中 F 表示合力，m 表示物体的质量，a 表示物体的加速度。

这个重要的公式表明了力对物体运动的影响。

三、解析受力分析和运动方程在动力学中，我们可以将受力分析和质点运动的关系用运动方程来描述。

运动方程包括位移方程、速度方程和加速度方程。

位移方程表示物体在某一段时间内的位移与速度和时间的关系，速度方程表示物体在某一时刻的速度与加速度和时间的关系，加速度方程表示物体在某一时刻的加速度与外力和质量的关系。

四、应用示例：自由落体运动自由落体运动是一个常见的物理现象，也是动力学的一个重要研究对象。

在自由落体运动中，物体只受到重力的作用，可以应用动力学解析受力分析和质点运动的关系来研究其运动情况。

通过受力分析可以得到物体受到的重力与其质量之间的关系，通过质点运动方程可以得到物体的速度和位移随时间的变化规律。

总结：动力学解析受力分析和质点运动的关系是物理学中的重要内容。

通过受力分析可以得到物体受力的合力，然后应用牛顿第二定律可以得到物体的加速度。

再结合运动方程，我们可以得到物体的运动规律。

这些理论和方法在物理学的各个领域都有广泛的应用，对于理解物体运动和力的作用具有重要意义。

网上作业系统1、告知作业网站的网址：222.18.54.19\homework。

2、告知学生用户的初始密码都是：123。

3、开学三周之内改选过教学班的学生，需要同时利用作业系统的“选课”功能更改一下选课，使作业系统中的选课与教务处网站上的选课结果相同。

4、开学后才选课的学生，可先通过作业系统提交一份登录申请，并等候教师审批。

20121121例7-11 导槽滑块机构。

已知：曲柄OA = r ，匀角速度ω转动，连杆AB 的中点C 处连接一滑块C 可沿导槽O 1D 滑动，AB =l ，图示瞬时O 、A 、O 1三点在同一水平线上, OA ⊥AB , ∠AO 1C =θ=300。

求：该瞬时O 1D 的角速度角加速度。

【解】OA , O 1D 均作定轴转动, AB 作平面运动。

（1）研究AB : , 图示位置, 作瞬时平动, 所以ωωr v v r v A c B ===;ωr v A =（2）用合成运动方法，求O 1D 杆上与滑块C接触的点的速度。

动点: AB 杆上C (或滑块C ),动系: O 1D 杆, 静系: 机架绝对运动：曲线运动，方向↓相对运动：直线运动，，方向// O 1D牵连运动：定轴转动，，方向⊥O 1Dωr v v c a ==?=r v ?=e v根据，作速度平行四边形r e a v v v +=ωωθr r v v C e 2330cos cos ==⋅=∴ ωθωωωl r l r C O v C O v e D O D O e 23sin /2231111===∴⋅= 又这是一个需要联合应用点的合成运动和刚体平面运动理论求解的综合性问题。

注意事项1、一定要多做题2、讲课顺序基本按照课本顺序；3、做作业时把作业写在纸上，交作业纸，不要交作业本。

不一定要把题全抄写，写清题意即可；但解题过程应尽量详细，养成一个良好习惯；不允许抄袭作业。

做作业时注意应该：单独取出研究对象，所取物体应标注名称、符号，每个力应有标号；画受力图；4、交作业时间为每周周一，要求每人都做作业，但不一定每次都要求全部交，按照要求交。