模态参数识别的频域方法

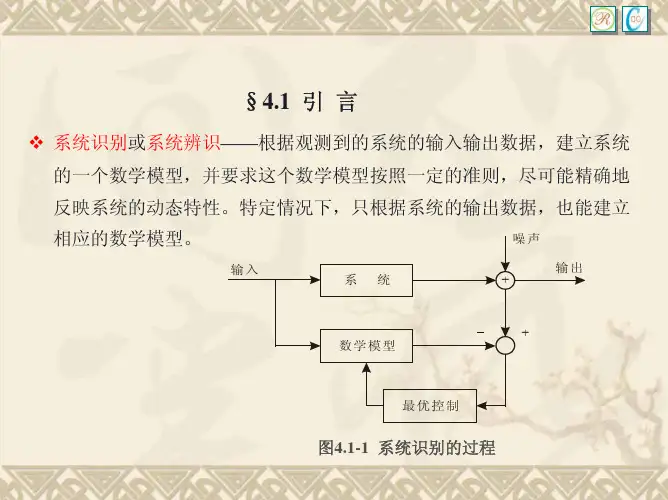
第三章模态参数辨识的频域方法在系统辨识中，模态参数是描述系统特性的重要指标，通过模态参数的辨识可以揭示系统的固有振动频率、阻尼比和模态形态等信息。

频域方法是一种常用的模态参数辨识方法，可以通过对系统在不同频率下的响应数据进行分析，得到系统的模态参数。

本文将介绍频域方法的原理和具体实施步骤。

频域方法的基本原理是在频域内拟合系统的频率响应函数，从而得到系统的模态参数。

具体实施步骤包括数据采集、信号处理和模态参数辨识。

首先，需要采集系统在不同频率下的响应数据。

使用激励信号激发系统，在传感器上采集到系统的响应信号。

为了得到较好的频率响应函数拟合结果，应该在不同频率下采集足够多的数据，并保证数据的信噪比较高。

其次，需要对采集到的响应数据进行信号处理。

首先，对采集数据进行预处理，包括去除噪声、滤波和降采样等操作，以提高数据质量。

然后，对处理后的数据进行频谱分析，可以使用傅里叶变换将时域信号转换为频域信号，然后计算频谱密度谱或功率谱密度谱等频域指标。

最后，通过拟合频率响应函数，得到系统的模态参数。

根据系统的特点，可以选择适合的频率响应函数进行拟合。

常见的选择包括模态曲线法、有限点法和广义谱方法等。

根据所选择的频率响应函数，通过最小二乘法等数值方法，拟合得到系统的模态参数，包括固有频率、阻尼比和振型等。

频域方法在模态参数辨识中具有以下优点：首先，由于仅对系统响应数据进行频域分析，不需要准确的系统模型，因此对于实际系统来说具有较高的适应性。

其次，频域方法能够较好地提取系统的模态信息，对于系统的非线性特性和随机性能够较好地处理。

此外，频域方法比较直观且易于实施，是一种常用的模态参数辨识方法。

总结来说，频域方法是一种常用的模态参数辨识方法，通过对系统在不同频率下的响应数据进行频域分析，可以得到系统的模态参数。

该方法具有较高的适应性和处理能力，是一种实用的系统辨识工具。

振动模态分析理论与应用模态参数识别频域法当系统阻尼为比例阻尼或小阻尼时，阻尼矩阵经模态坐标变换后可以对角化，模态参数为实数，频响函数可按实模态展开。

若在p 点激励，在l 点测量，则频响函数可表示为对于粘性阻尼有∑12ωωξ2ωω1)ω(Ni i i i lplp j D H =+=对于结构阻尼有∑12ωω1)ω(Ni i ilp lp jg D H =+=以上两式即为实模态参数识别的基本公式 6.1 实模态识别图解法6.1.1 共振法这是一种经典的模态分析方法，其基本思想是：当激励频率在系统某阶固有频率r ω附近时，该阶模态导纳便起主导作用，其余各阶模态导纳的影响可忽略不计。

即 )ω(≈)ω(lpr lp H H 此时，整个系统等效于一个单自由度系统。

利用幅频特性和相频特性，便可确定系统的模态参数（参看图6-1）。

在待测结构上选择l 个测试点，求其中某点P 对所有各点的位移导纳。

点数l 一般应等于或大于拟选的模态数N （自由度数）。

则p 点对任意点l 的位移导纳可作如下处理：当激振频率在r 阶固有频率附近时有()()2222∞12ωωξ4ωω1≈ωωξ2ωω1)ω(∑++==rrir lp i ii i ilp lp j D j D H因此，测得的幅频曲线)ω(lp H 的第r 个峰值位置（共振频率点），便可近似确定r 阶固有频率r ω。

由r ω两侧半功率带宽，可以确定r 阶模态阻尼比)ω2/Δω(ξr r =。

由r ω处位移有()rrlp rlpD H ξ2)ω(=所以 ()()rlprrlpH D ωξ2= 由因为 ()rprlr rlp kD φφ=故在令pr φ的值等于1（振型中各元素具有确定的比例，其绝对值可认为地指定，不妨取第r 阶振型第p 个元素pr φ的值等于1）时，由原点导纳曲线的峰值可得r 阶模态刚度为)ω(ξ21r pp r r H k =此外，当r ωω=时，l 个导纳的幅值分别为r r pr r r p k H ξ2φφ|)ω(|11= rr prr r p k H ξ2φφ|)ω(|22=rr pr lr r lp k H ξ2φφ|)ω(|=写成矩阵形式=lrr rr r pr r lp r p r p k H H H φφφξ2φ|)ω(||)ω(||)ω(|2121因此，第r 阶振型为{}±±±==|)ω(||)ω(||)ω(|φφφφ2121r lp rpr p lrrrrH H H为表示振型的几何形状，上试中各导纳幅值应考虑其相位，可用正负号表示同相或反相，对于实模态，其振型向量的各分量都是实数，且只有大小和正负之差。

模态参数辨识的频域方法吕毅宁目录模态参数辨识的频域方法 (1)单点输入单点输出(SISO) (1)图解法............................................................................................................ 1 频域多参考点模态参数辨识（MIMO ） ............................................................ 2 频域模态测试和参数辨识的可控性和可观性. (5)单点输入单点输出(SISO) 图解法1) 峰值检测 半功率点)(21)()(21r j H j H j H ωωω== （1） rr ωωωξ212-=（2）2) 模态检测()ir rjr r rrij rjrir r r r r jr ir r r ij Q A Q j j Q j H ψσψσσψψωσωψψω-=-=-=+-=)()(（3）式中，r Q 是模态比例换算因子。

在上式中，()r ij A 是模态质量r m 和模态刚度r k 的函数，又由下面的关系2r rrm k ω= （4）联立即可求得模态质量和模态刚度。

3) 圆拟合法 固有频率max ==ωωωd dsrr （5）振型rer I ij g k H 1-=（6）jrir rer k k ϕϕ=（7）er k 是等效模态刚度，rrr k g η=是等效结构阻尼。

()r ij r Iijir rr jr R g k )(2==-H ϕϕ （8）模态阻尼rg )1(2tan 211ωα-=（9）rg )1(2tan 222-=ωα （10）2tan2tan22112ωωω+-=rr g （11）模态刚度 由rer r I ij g k H 1)1(-==ω （12）可得rr Iij er g H k )1(1=-=ω （13）模态质量2r rr k m ω=（14）其他方法，如正交多项式曲线拟合法，非线性优化辨识方法。

模态参数辨识的频域方法张永强高级工程师靖江泰斯特电子有限公司西北工业大学振动工程研究所•分析分量法•导纳园识别方法•正交多项式曲线拟合N | H阿二工r=\. _ g rK er(1-研(i-研r+g；等效刚度与测点与激励点有关•分量分析法•将频响函数分成实部风量和虚部分量进行分析。

-基本公式和主模态概念・N自由度结构系统结构，p点激励1点响应的实模态频响函数© = col co r•主模态：当趋于某阶模态的固有频率时，该模态起主要作用此时起主要作用的模态成为主导模态，或叫主模态。

•主模态附近频响函数-若模态密度不很大，各阶模态比较远-则其余模态频响函数在该主模态附近较小，且几乎不随频率变化-因此在第r阶模态附近可用剩余模态表示频响函数H阿二H㈣=科 +；+ (观+圧)实频图与虚频图・剩余模态与频率无关・在实频图和虚频图上相・当于将横坐标平移一距离•此平行线又名剩余柔度线二模态参数的确定2・固有频率的确定-实频线与剩余柔度线交点确定-虚频线的峰值确定-峰值较尖，确定容易-剩余柔度尺寸无影响S）实頻图（b）邃频图-因此用虚频峰值确定更好•阻尼比匕或5的确定•用半功率带宽来确定A© -G5h-G)a・结构阻尼系统阻尼比系数一v CD K - 0)gr = 或Sr =；©•粘性阻尼系统阻尼比系数或r "T-模态振型的确定•对© =1主模态(不含剩余柔度)•测岀L 个测点的值(1=1, 2, 3, L)•单点激振时一臥为常数,所以上式即为模态振型。

侃迈二1)｝广 砒@二久%> —— <%>■ ■• 砒 @=-K&■ • •Lxl厶xl•对激励点归一化的振型勺〃.=1侃@=1)}.=—点泌爲-模态刚度的确定•取原点频响函数且对原点归一化H；p(© = D = -•模态刚度-模态质量的确定M仝-分量分析法的特点・简单方便，许多信号分析仪有实虚频图分析能力；・当模态密度不高时，有一定的精度；:・峰值有误差时，直接影响辨识精度；: ・模态密集时，用半功率带宽确定模态阻尼，误差较大；•模态密集时剩余模态不能用复常数表示，辨识精度受影响;・图解法受图解精度的影响。

模态参数识别中常用的三种频域方法探究1 引言与时域方法直接作用于采样数据，保留全部信息的做法不同，频域方法常采用平均周期图法对数据进行预处理，进而得到与窗口等长的频域信号。

如上不同，使得频域方法的抗噪性及运算效率更高，更适用于现场测试数据的实时处理。

但是，频域方法的假定较多，加之仅基于输出的识别方式具有先天理论的不足，其识别结果能否满足工程要求也受到了较多的讨论。

本文试图通过有限元分析及三种常用频率分析方法的相互对比，验证算法应用于复杂结构时可靠性。

2 峰值法（PP）及频域分解法（FDD）PP及FDD均利用白噪聲假定下功率谱密度函数在固有频率处出现峰值的特性直观识别特征频率。

两者的不同在于离散结构的方式不同：PP通过诸如小阻尼、频率离散分布等一系列假定直接使系统解耦为单自由度体系；FDD在保留小阻尼假定的基础上，放宽了峰值由单一模态贡献（频率离散分布）的假定，考虑相邻模态的影响（实际中通常不多于两阶），转用物理概念更明确的奇异值分解（相当于进行了维纳滤波）离散系统，使其结果较PP具有更广的适用性。

3 多参考最小二乘复频域法（PolyMAX）PolyMAX方法利用线形时不变系统传递函数在数学上总能以右矩阵分式模型（Right Matrix Fraction Description-RMFD）表示的性质。

在白噪声假定下，将功率谱密度函数以RMFD模型描述，其某测点o与各参考点之间的互谱密度记为：其中，p为系统阶次，Ωr=e-jωΔtr为多项式基函数，Δt=1/fs为采样时间，分子系数矩阵βor∈R1×m，分母系数矩阵αr∈Rm×m，另外，定义α=[α0，α1…αp]T ∈Rm（p+1）×m再利用实测数据与理论结果的差值构建加权线形最小二乘成本函数，并对其自变量α、βo求偏导，即可得到系数矩阵α。

详尽推导过程可参见文献。

4 应用实例虹桥位于常德市白马湖公园内，是一座单箱单室钢箱梁人行天桥，桥宽5.5m，跨径组合（27+33+33+27）m，如图1所示。

最小二乘复频域法（PolyMax ）LMS 公司推出的PolyMax 模态识别方法,属于多自由度时域识别法,也称作多参考点最小二乘复频域法( Polyreference least squares complex frequency domain method)， 是最小二乘复频域法(LSCF)的多输入形式，是一种对极点和模态参预因子进行整体估计的多自由度法,一般首先通过实验建立稳态图，以判定真实的模态频率、阻尼和参预因子；建立可以线性化的直交矩阵分式模型，然后基于正则方程缩减最小二乘问题,得到压缩正则方程,于是模态参数可以通过求解最小二乘问题得到。

该方法集合了多参考点法和LSCF 方法的优点,可以得出非常清晰的稳态图,并且密集空间可以被分离出来,尤其在模态较密集的系统(动力总成系统)，或者FRF 数据受到严重噪声污染的情况下仍可以建立清晰的稳态图，识别出高度密集的模态，对每一个模态的频率、阻尼和振型都有很好的识别精度,是国际最新发展并流行的基于传递函数的模态分析方法。

其基本思想如下： （1）建立频率响应函数模型多参考点最小二乘复频域识别技术（PRLSCF 或PolyMAX ）要以频响函数矩阵作为识别的初始数据，其数学模型采用右矩阵分式模型来描述。

在频域中，系统输出o （0,2,1N o =， 其中0N 为输出点数）和全部输入的关系可用右矩阵分式模型（RMFD ）来描述，右矩阵分式模型的表达式为()()()1-=ωωωD U H o o （1）式中：()i N l o C H ⨯∈ω—理论频响函数的第o 行，i N 是输入点数，即激励数； ()i N l o C U ⨯∈ω—分子多项式行向量；()i i N N o C D ⨯∈ω—分母多项式矩阵。

且()ωo U 和()ωo D 可以表示成如下形式：()()()∑=⋅=Nr or r o B Z U 0ωω （0,2,1N o =） （2）()()()∑=⋅=Nr r r o A Z D 0ωω （3）式中：N —多项式阶次其中分母系数矩阵i i N N r R A ⨯∈和分子系数行向量i N l or R B ⨯∈是待估计的参数。

模态参数辨识方法——综述模态参数辨识方法综述摘要：本文对模态分析和模态参数识别进行了综述，对当前识别方法的原理、识别精度及适用条件进行阐述和比较，提出环境激励下模态参数识别方法需解决的关键问题及模态分析在缺陷检测和结构优化中作用。

关键词：模态分析模态参数识别模态分析与缺陷检测结构工作模态0引言模态分析是将线性时不变系统振动微分方程组中的物理坐标变换为模态坐标，使方程组解耦，成为一组以模态坐标及模态参数描述的独立方程，坐标变换的变换矩阵为振型矩阵，其每列即为各阶振型。

模态是机械结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型。

这些模态参数可以由计算或试验分析取得，这样一个计算或试验分析过程称为模态分析。

振动模态是弹性结构固有的、整体的特性。

如果通过模态分析方法搞清楚了结构物在某一易受影响的频率范围内，各阶主要模态的特性，就可能预知结构在此频段内，在外部或内部各种振源作用下实际振动响应，而且一旦通过模态分析知道模态参数并给予验证，就可以把这些参数用于（重）设计过程，优化系统动态特性，或者研究把该结构连接到其他结构上时所产生的影响。

模态分析的最终目标是识别出系统的模态参数，为结构系统的振动分析、振动故障诊断和预报、结构动力特性的优化设计提供依据。

解析模态分析可用有限元计算实现，而实验模态分析则是对结构进行可测可控的动力学激励，由激振力和响应的信号求得系统的频响函数矩阵，再在频域或转到时域采用多种识别方法求出模态参数，得到结构固有的动态特性，这些特性包括固有频率、振型和阻尼比等。

有限元法是当前分析机械结构模态的主要方法，很多学者研究了单裂缝和多裂缝缺陷对不同结构动态特性的影响，但这些研究仅局限于出现缺陷结构的当前状态，考虑到缺陷在机械结构使用过程中的扩展，提出了模态分析与缺陷扩展理论相结合的方法分析缺陷的发展趋势，便于机械结构剩余寿命的评估，使已达到设计寿命的结构在失效前仍然发挥其功能，节约了经济成本。

机械系统的模态分析与振动模式识别引言：在工程领域中，机械系统的振动问题一直被人们广泛关注。

振动问题不仅会导致设备的性能下降，还可能引发设备的损坏和故障。

因此，对机械系统的振动情况进行准确的模态分析和振动模式识别，对于提高设备的稳定性和寿命具有重要意义。

本文将从机械系统的模态分析和振动模式识别的基本原理、方法和应用案例展开讨论。

一、机械系统的模态分析1.1 模态的概念模态是指机械系统在振动过程中的特定振动状态。

每个模态具有特定的频率、振型和振幅。

通过模态分析，我们可以了解机械系统不同振动模态的特性，从而更好地进行系统设计和优化。

1.2 模态分析的方法模态分析是通过测量和计算机处理振动信号来研究机械系统的特征模态的方法。

常见的模态分析方法有频域法、时域法和模型法。

1.2.1 频域法频域法是通过将振动信号傅里叶变换到频域，分析信号的频率成分和频谱特征，确定系统的共振频率和模态参数。

常用的频域分析方法有快速傅里叶变换（FFT）、谱分析等。

1.2.2 时域法时域法通过观察振动信号的波形和振动传递函数的响应，分析系统的振动特性。

时域分析方法包括自相关函数、互相关函数和功率谱等。

模型法是通过建立数学模型描述机械系统的振动特性，利用数学模型求解系统的模态参数。

常见的模型法有有限元法、辛普森法、辛普森规范化法等。

1.3 模态分析的应用模态分析广泛应用于机械系统的动态特性研究、结构优化、故障诊断和设计验证等领域。

例如，在风力发电机的设计中，通过模态分析可以确定发电机的受力、振动和噪声情况，进而优化设计和提高发电效率。

二、振动模式识别2.1 振动模式的概念振动模式指的是机械系统在振动过程中呈现出的不同振动形态。

不同的振动模式对应着不同的频率、振型和振幅。

通过振动模式识别，我们可以准确地确定机械系统的振动特性，并及时发现和处理潜在的故障或异常。

2.2 振动模式识别的方法振动模式识别是通过对振动信号进行特征提取和模式分类，来实现对机械系统振动信息的理解和判断。