下载文档原格式
第7章网络计划方法PERT：计划评审方法CPM：关键路线法用于大型项目的进度管理。
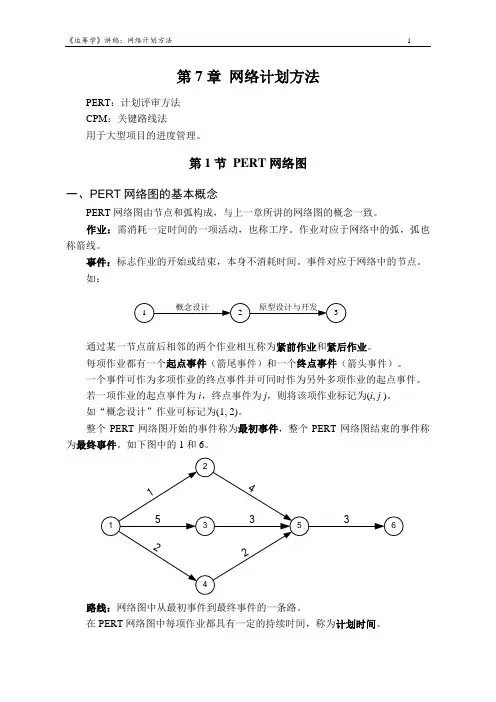
第1节PERT网络图一、PERT网络图的基本概念PERT网络图由节点和弧构成，与上一章所讲的网络图的概念一致。
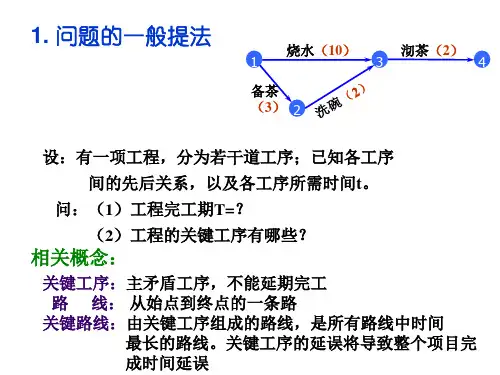
作业：需消耗一定时间的一项活动，也称工序。
作业对应于网络中的弧，弧也称箭线。
事件：标志作业的开始或结束，本身不消耗时间。
事件对应于网络中的节点。
如：通过某一节点前后相邻的两个作业相互称为紧前作业和紧后作业。
每项作业都有一个起点事件（箭尾事件）和一个终点事件（箭头事件）。
一个事件可作为多项作业的终点事件并可同时作为另外多项作业的起点事件。
若一项作业的起点事件为i，终点事件为j，则将该项作业标记为(i, j )。
如“概念设计”作业可标记为(1, 2)。
整个PERT网络图开始的事件称为最初事件，整个PERT网络图结束的事件称为最终事件。
如下图中的1和6。
路线：网络图中从最初事件到最终事件的一条路。
在PERT网络图中每项作业都具有一定的持续时间，称为计划时间。
路线的长度：路中各项作业的计划时间之和。
网络中通常存在多条不同的路线。
关键路线：所有路线中计划时间之和最长的那条路。
如上图中1—3—5—6即为关键路路线，其时间长度为11小时。
二、建立PERT 网络图的准则1. 一项作业用一条箭线表示；每项作业的终点事件编号应大于起点事件编号。
2. 两个事件之间只能有一条箭线，若存在两项或更多项作业，则需引入虚作业进行表示，如下图。
3. 作业之间的几种典型关系在网络图中的表示：4. PERT 网络图有唯一的最初事件和唯一的最终事件。
5. PERT 网络图中不允许出现回路。
6. PERT 网络图的绘制应进行适当的布局：尽量避免箭线之间出现交叉；使各条箭线尽量按从左到右的方向展开。
7. 在实际应用中，对大型项目，可绘制多个层次的网络图。
高层次网络图中的一项或几项作业，可展开绘制成一张低层次的网络图。
三、PERT网络图的绘制例1(1)某项工程由11项作业组成，各项作业之间的先后展开关系如下：解：绘制网络图的步骤：(1) 由最初节点画出所有无紧前作业的作业；(2) 逐条绘制紧前作业已全部画出的作业：将全部紧前作业指向同一个终点事件，再从该终点事件画出当前作业。
《运筹学》重要知识点解析和例题分析第六部分一．图的基本概念 定义一个图G 是指一个二元组(V(G),E(G)).即图是由点及点之间的联线所组成。
其中: 1）图中的点称为图的顶点(vertex).记为：v2）图中的连线称为图的边(edge).记为：,i j e v v ⎡⎤=⎣⎦.,i j v v 是边 e 的端点。
3）图中带箭头的连线称为图的弧(arc).记为：(),i j a v v =.,i j v v 是弧 a 的端点。
—— 要研究某些对象间的二元关系时.就可以借助于图进行研究 分类▪ 无向图：点集V 和边集E 构成的图称为无向图(undirected graph).记为： G(V.E)—— 若这种二元关系是对称的.则可以用无向图进行研究▪ 有向图：点集V 和弧集A 构成的图称为有向图(directed graph) .记为：D(V.A)—— 若这种二元关系是非对称的.则可以用有向图进行研究▪ 有限图: 若一个图的顶点集和边集都是有限集.则称为有限图.只有一个顶点的图称为平凡图.其他的所有图都称为非平凡图.图的特点：1 图反映对象之间关系的一种工具.与几何图形不同。
2 图中任何两条边只可能在顶点交叉.在别的地方是立体交叉.不是图的顶点。
3 图的连线不用按比例画.线段不代表真正的长度.点和线的位置有任意性。
4 图的表示不唯一。
如：以下两个图都可以描述“七桥问题”。
点(vertex)的概念1 端点：若e =[u.v] ∈E.则称u.v 是 e 的端点。
2 点的次：以点 v 为端点的边的个数称为点 v 的次.记为：()d v 。
在无向图G 中.与顶点v 关联的边的数目(环算两次),称为顶点v 的度或次数.记为()d v 或 dG(v).在有向图中.从顶点v 引出的边的数目称为顶点v 的出度.记为d+(v).从顶点v 引入的边的数目称为v 的入度.记为d -(v). 称()d v = d+(v)+d -(v)为顶点v 的度或次数． 3 奇点：次为奇数的点。
