运筹学第六章网络计划作业答案

《运筹学》第六章排队论习题转载请注明1. 思考题（1）排队论主要研究的问题是什么；（2）试述排队模型的种类及各部分的特征；（3）Kendall 符号C B A Z Y X /////中各字母的分别代表什么意义；（4）理解平均到达率、平均服务率、平均服务时间和顾客到达间隔时间等概念； （5）分别写出普阿松分布、负指数分布、爱尔朗分布的密度函数，说明这些分布的主要性质；（6）试述队长和排队长；等待时间和逗留时间；忙期和闲期等概念及他们之间的联系与区别。

2．判断下列说法是否正确（1）若到达排队系统的顾客为普阿松流，则依次到达的两名顾客之间的间隔时间服从负指数分布；（2）假如到达排队系统的顾客来自两个方面，分别服从普阿松分布，则这两部分顾客合起来的顾客流仍为普阿松分布；（3）若两两顾客依次到达的间隔时间服从负指数分布，又将顾客按到达先后排序，则第1、3、5、7，┉名顾客到达的间隔时间也服从负指数分布； （4）对1//M M 或C M M //的排队系统，服务完毕离开系统的顾客流也为普阿松流； （5）在排队系统中，一般假定对顾客服务时间的分布为负指数分布，这是因为通过对大量实际系统的统计研究，这样的假定比较合理；（6）一个排队系统中，不管顾客到达和服务时间的情况如何，只要运行足够长的时间后，系统将进入稳定状态；（7）排队系统中，顾客等待时间的分布不受排队服务规则的影响；（8）在顾客到达及机构服务时间的分布相同的情况下，对容量有限的排队系统，顾客的平均等待时间少于允许队长无限的系统；（9）在顾客到达分布相同的情况下，顾客的平均等待时间同服务时间分布的方差大小有关，当服务时间分布的方差越大时，顾客的平均等待时间就越长； （10）在机器发生故障的概率及工人修复一台机器的时间分布不变的条件下，由1名工人看管5台机器，或由3名工人联合看管15台机器时，机器因故障等待工人维修的平均时间不变。

3．某店有一个修理工人，顾客到达过程为Poisson 流，平均每小时3人，修理时间服从负指数分布，平均需19分钟，求： （1）店内空闲的时间； （2）有4个顾客的概率； （3）至少有一个顾客的概率； （4）店内顾客的平均数； （5）等待服务的顾客数； （6）平均等待修理的时间；（7）一个顾客在店内逗留时间超过15分钟的概率。

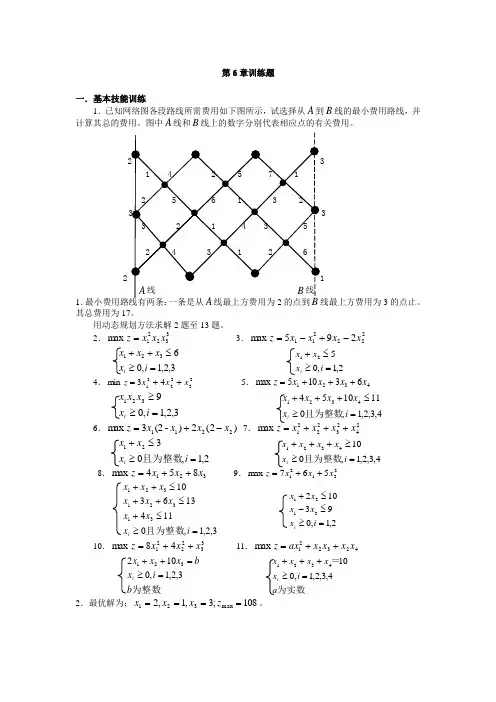
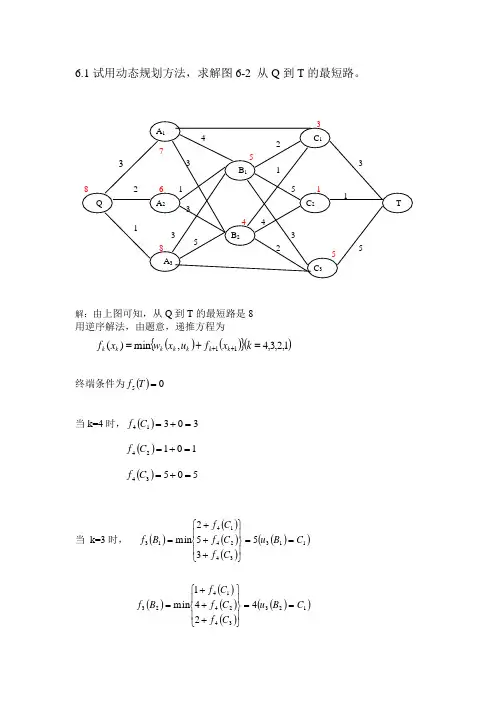
6.1试用动态规划方法，求解图6-2 从Q 到T 的最短路。

解：由上图可知，从Q 到T 的最短路是8用逆序解法，由题意，递推方程为()(){}()1,2,3,4,min )(11=+=++k x f u x w x f k k k k k k k终端条件为()05=T f当k=4时，()30314=+=C f()10124=+=C f()50534=+=C f当 k=3时， ()()()()()()113342414135352min C B u C f C f C f B f ==⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+++=()()()()()()123342414234241min C B u C f C f C f B f ==⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+++=当k=2时，()()()()()212231312734min B A u B f B f A f ==⎭⎬⎫⎩⎨⎧++=()()()()()122231322731min B A u B f B f A f ==⎭⎬⎫⎩⎨⎧++=()()()()()132231332853min B A u B f B f A f ==⎭⎬⎫⎩⎨⎧++=当k=1 时，()()()()()()2132221218123min A Q u A f A f A f Q f ==⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+++=最优解策略为()2*1A Q u = ()12*2B A u = ()11*3C B u = ()T C u =1*4最短路长为86.2用动态规划方法求解 （1）3221max x x x F ⋅⋅=⎩⎨⎧=≥=++3,2,1,04..321i x x x x t s i解：3211x x x S ++=322x x S += 33x S = 121x S S +=232x S S += 33x S =()(){}3max 22022222f x s f sx ⋅=≤≤=(){}2220222max x s x sx -⋅≤≤由导数法求得，当3222s S =时，()22x f 有最大值27432s ()(){}22140111max x f x s f x ⋅=≤≤=()⎭⎬⎫⎩⎨⎧⋅=≤≤274max 32140111s x s f x =()()⎭⎬⎫⎩⎨⎧-⋅=≤≤2744max 31140111x x s f x解得：11=x 时，()4max 11=x f∴ ()⎪⎩⎪⎨⎧+==++322323241x x x x x∴⎩⎨⎧==1232x x ∴1,2,1321===x x x （2）321232223222124222min x x x x x x x x F ---+-++=⎩⎨⎧=≥=++3,2,1,03..321i x x x x t s i解： 31=S 112x S S -= 223x S S -=()(){}41min 23333--==x s f x s =(){}4123--s()()(){}4112min 2322222--+-=≤s x s f x x=()(){}411222222---+-x s x=1422224222222222222+-+-+-++-x s x x s s x x()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+-=≤222221413423221min 1s s x s f x =()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛--+-≤1342632321min 21212141x x x x=()()112194219212221211121--+-++-++-x x x x x x =96930915121+-x x =30301-x =011=x6.3 有四台设备分给甲，乙，丙，丁四厂，各厂盈利如表6-6所示。

《管理运筹学》各章的作业----复习思考题及作业题第一章绪论复习思考题1、从运筹学产生的背景认识本学科研究的内容和意义。

2、了解运筹学的内容和特点，结合自己的理解思考学习的方法和途径。

3、体会运筹学的学习特征和应用领域。

第二章线性规划建模及单纯形法复习思考题1、线性规划问题的一般形式有何特征？2、建立一个实际问题的数学模型一般要几步？3、两个变量的线性规划问题的图解法的一般步骤是什么？4、求解线性规划问题时可能出现几种结果，那种结果反映建模时有错误？5、什么是线性规划的标准型，如何把一个非标准形式的线性规划问题转化成标准形式。

6、试述线性规划问题的可行解、基础解、基础可行解、最优解、最优基础解的概念及它们之间的相互关系。

7、试述单纯形法的计算步骤，如何在单纯形表上判别问题具有唯一最优解、有无穷多个最优解、无界解或无可行解。

8在什么样的情况下采用人工变量法，人工变量法包括哪两种解法？9、大M法中，M的作用是什么？对最小化问题，在目标函数中人工变量的系数取优质参考资料(2)x i3(1)什么？最大化问题呢？10、什么是单纯形法的两阶段法？两阶段法的第一段是为了解决什么问题？在怎样 的情况下，继续第二阶段？作业题:1 、把以下线性规划问题化为标准形式：(i) max z= x i -2x 2 +x 3s.t.x i +x 2 +x 3 w i2 2x i +x 2 -x 3> 6 -x i+3x 2=9x i , x 2,x 3> 0(2)min z= -2x i -x 2 +3x 3 -5x 4s.tx i +2x 2 +4x 3 -x 462x i +3x 2-x 3 +x 4 = i2x i+x 3+x 4w 4x i ,x 2,x 4maxz= x i+3x 2 +4x 3(3)s.t.3x i +2x 2w i3x 2 +3x 3w i72x i+x 2 +x 3 =i3x i ,x 3> 02 、用图解法求解以下线性规划问题max z= x 1+3x 2s.t.x i +X 2< 10-2x i +2x 2 w 12 X i w 7 x i ,X 2 > 0min z= x 1 -3x 2 s.t.2x 1 -x 2 w 4 x i +X 2> 3x2 w 5 w4x1, X2 > 03、在以下问题中，列出所有的基，指出其中的可行基，基础可行解以及最优解max z= 2x1 +x2 -x 3s.t. x1 + x2 +2x3 < 6x1 +4x2 -x 3 < 4x1, x2, x3 > 04、用单纯形表求解以下线性规划问题(1) max s.t. z= x1x12x 1-x 1x 1, -2x 2 +x3+X2 +X3 w 12 +X2 -x 3 w 6+3X2X2,w 9X3 > 0(2) min z= -2x 1 -X 2 +3X3 5X 4s.t x1 +2X 2 +4X3 -X 4 w 62x1 +3X 2 -X 3 +X4 w 12x1 +X3 +X4 w 4x1, X2, X3, X4 05、用大M法和两阶段法求解以下线性规划问题(1) MaX z= X1 +3X2 +4X3s.t. 3X 1 +2X2 w13X2 +3X3 w172X 1 +X2 +X3 =13X 1, X2, X3> 0(2) maX z= 2X 1 -X 2 +X3s.t. X1 +X2 -2X 3 w84X 1 -X 2 +X3 w22X 1 +3X2 -X 3 > 4X 1, X2, X3 > 06 、某饲养场饲养动物，设每头动物每天至少需要700克蛋白质、30克矿物质、100 毫克维生素。

运筹学习题答案第六章运筹学习题答案第六章第一节：线性规划线性规划是运筹学中的一种重要方法，它通过建立数学模型来解决实际问题。

在第六章中，我们学习了线性规划的基本概念和求解方法。

本节将针对第六章的习题提供详细的解答。

第1题：某公司生产两种产品，产品A和产品B。

每单位产品A的利润为5万元，每单位产品B的利润为4万元。

产品A每单位需要3个工时，产品B每单位需要2个工时。

公司每天有8个小时的工时可用。

求解公司每天应生产多少单位的产品A和产品B，才能使利润最大化？解答：设产品A的产量为x，产品B的产量为y。

根据题意可得以下线性规划模型：目标函数：Max Z = 5x + 4y约束条件：3x + 2y ≤ 8非负约束：x ≥ 0，y ≥ 0根据图形法，我们可以绘制出约束条件的图形，并找到最优解。

通过计算，我们得到最优解为x = 2，y = 1。

即公司每天应生产2个单位的产品A和1个单位的产品B，才能使利润最大化。

第2题：某公司有两个生产车间，分别生产产品A和产品B。

车间1每天可生产产品A 4个单位或产品B 2个单位；车间2每天可生产产品A 3个单位或产品B 6个单位。

产品A的利润为3万元，产品B的利润为2万元。

公司每天有8个小时的工时可用。

求解公司每天应生产多少单位的产品A和产品B，才能使利润最大化？解答：设车间1生产的产品A的单位数为x1，车间2生产的产品A的单位数为x2。

设车间1生产的产品B的单位数为y1，车间2生产的产品B的单位数为y2。

根据题意可得以下线性规划模型：目标函数：Max Z = 3x1 + 2x2 + 2y1 + 3y2约束条件：4x1 + 3x2 ≤ 82x1 + 6x2 ≤ 8非负约束：x1 ≥ 0，x2 ≥ 0，y1 ≥ 0，y2 ≥ 0通过计算，我们得到最优解为x1 = 2，x2 = 0，y1 = 0，y2 = 1。

即公司每天应生产2个单位的产品A和1个单位的产品B，才能使利润最大化。

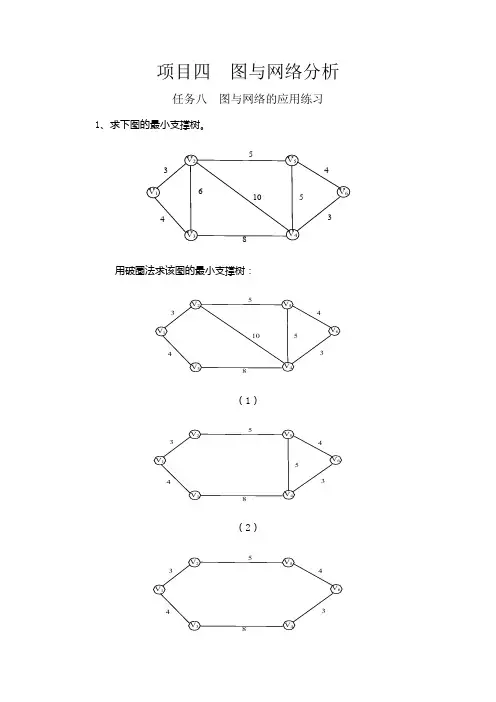
项目四图与网络分析任务八图与网络的应用练习1、求下图的最小支撑树。

用破圈法求该图的最小支撑树：（1）（2）（3）（4）2、分别用破圈法和避圈法求下列各个图的最小支撑树。

a-1：用破圈法求图a的最小支撑树：a-2：用避圈法求图a的最小支撑树：b-1：用破圈法求图b 的最小支撑树：b-2：用避圈法求图b 的最小支撑树：3、用标号法求下图中1v 至7v 的最短路。

1）标号过程（1）初始化；令起点v 1的标号为P ，记做P(1) =0；令其余各点的标号为T ，记做T(i)=∞；（2）计算T标号：刚得到P标号的点为v1，考虑所有与v1相邻的T标号点v 2、v3、v5，修改v2、v3、v5的T标号为：T(2)=min[T(2)，P(1)+d12]=min[+∞，0+4]=4T(3)=min[T(3)，P(1)+d13]=min[+∞，0+3]=3T(5)=min[T(5)，P(1)+d15]=min[+∞，0+5]=5 （3）确定P标号：在所有的T标号点中，找出标号值最小的点标上P标号。

T(2)= 4 T(3) =3 T(4) =+∞T(5)=5 T(6)= +∞ T(7)= +∞令P(3)=3。

（4）计算T标号：刚得到P标号的点为v3，考虑所有与v3相邻的T标号点v 6，修改v6的T标号为：T(6)=min[T(6)，P(3)+d36]=min[+∞，3+2]=5 （5）确定P标号：在所有的T标号点中，找出标号值最小的点标上P标号。

T(2)= 4 T(4) =+∞ T(5)=5 T(6)= 5 T(7)= +∞令P(2)=4。

（6）计算T标号：刚得到P标号的点为v2，考虑所有与v2相邻的T标号点v 5，修改v5的T标号为：T(5)=min[T(5)，P(2)+d25]=min[5，4+1]=5（7）确定P标号：在所有的T标号点中，找出标号值最小的点标上P标号。

T(4) =+∞ T(5)=5 T(6)= 5 T(7)= +∞令P(5)=5。

《运筹学》第六章排队论习题1. 思考题（1）排队论主要研究的问题是什么；（2）试述排队模型的种类及各部分的特征；（3）Kendall 符号C B A Z Y X /////中各字母的分别代表什么意义；（4）理解平均到达率、平均服务率、平均服务时间和顾客到达间隔时间等概念； （5）分别写出普阿松分布、负指数分布、爱尔朗分布的密度函数，说明这些分布的主要性质；（6）试述队长和排队长；等待时间和逗留时间；忙期和闲期等概念及他们之间的联系与区别。

2．判断下列说法是否正确（1）若到达排队系统的顾客为普阿松流，则依次到达的两名顾客之间的间隔时间服从负指数分布；（2）假如到达排队系统的顾客来自两个方面，分别服从普阿松分布，则这两部分顾客合起来的顾客流仍为普阿松分布；（3）若两两顾客依次到达的间隔时间服从负指数分布，又将顾客按到达先后排序，则第1、3、5、7，┉名顾客到达的间隔时间也服从负指数分布； （4）对1//M M 或C M M //的排队系统，服务完毕离开系统的顾客流也为普阿松流； （5）在排队系统中，一般假定对顾客服务时间的分布为负指数分布，这是因为通过对大量实际系统的统计研究，这样的假定比较合理；（6）一个排队系统中，不管顾客到达和服务时间的情况如何，只要运行足够长的时间后，系统将进入稳定状态；（7）排队系统中，顾客等待时间的分布不受排队服务规则的影响；（8）在顾客到达及机构服务时间的分布相同的情况下，对容量有限的排队系统，顾客的平均等待时间少于允许队长无限的系统；（9）在顾客到达分布相同的情况下，顾客的平均等待时间同服务时间分布的方差大小有关，当服务时间分布的方差越大时，顾客的平均等待时间就越长； （10）在机器发生故障的概率及工人修复一台机器的时间分布不变的条件下，由1名工人看管5台机器，或由3名工人联合看管15台机器时，机器因故障等待工人维修的平均时间不变。

3．某店有一个修理工人，顾客到达过程为Poisson 流，平均每小时3人，修理时间服从负指数分布，平均需19分钟，求： （1）店内空闲的时间； （2）有4个顾客的概率； （3）至少有一个顾客的概率； （4）店内顾客的平均数； （5）等待服务的顾客数； （6）平均等待修理的时间；（7）一个顾客在店内逗留时间超过15分钟的概率。

判断题判断正误，如果错误请更正第六章网络模型1.连通图G的部分树是取图G的点和G的所有边组成的树。

2.Dijkstra算法要求边的长度非负。

3.Floyd算法要求边的长度非负。

4.割集中弧的流量之和称为割量。

5.最小割集等于最大流量。

6.求最小树可用破圈法。

7.在最短路问题中，发点到收点的最短路长是唯一的。

8.在最大流问题中，最大流是唯一的。

9.最大流问题是找一条从发点到收点的路，使得通过这条路的流量最大。

10.容量Cij是弧（i,j）的实际通过量。

11.可行流是最大流的充要条件是不存在发点到收点的增广链。

12.任意可行流的流量不超过任意割量。

13.任意可行流的流量不小于最小割量。

14.可行流的流量等于每条弧上的流量之和。

15.Dijkstra算法是求最大流的一种算法。

16.避圈法（加边法）是：去掉图中所有边，从最短边开始添加，加边的过程中不能形成圈，直到有n条边（n为图的点数）。

17.连通图一定有支撑树。

18.μ是一条增广链，则后向弧上满足流量f>=0。

19.最大流量等于最大流。

20.旅行售货员问题是遍历每一条边的问题。

选择题在下列各题中，从4个备选答案中选出一个或从5个备选答案中选出2~5个正确答案。

第6章网络模型1.μ关于可行流f的增广链，则在μ上有 A 对任意（i，j）∈μ+，，有f ij<=c ij B对任意（i，j）∈μ+，，fij<=c ij C 对任意（i，j）∈μ-，有f ij<=c ij D 对任意（i，j）∈μ-，有f ij>0 E对任意（i，j）∈μ-，有f ij>=02.连通图G有n个点，其部分树是T ，则有 A T 有n点n条边 B T的长度等于G的每条边的长度之和。

C T有n个点n-1条边 D T 有n-1个点 n条边3.设P是图G 到Vs到Vt的最段短路，则有 A P的最短路长等于Vs到Vt的最大流量 B P的长度等于G的每条边的长度之和 C P的长度等于P的每条边的长度之和 D P有n 个点n-1 条边4.求最短路的计算方法有 A Dijkstra 法 B Floyd法 C 加边法 D 破圈法 EFord-fulkerson 算法5.求最大流的方法有 A Dijkstra 法 B Floyd法 C 加边法 D 破圈法 EFord-fulkerson 算法6.下列说法正确的是 A 割集是子图 B 割量等于割集中弧的流量之和 C 割量大于等于最大流量D 割量小于等于最大流量7.下列错误的结论是A 容量不超过流量 B 流量非负 C 容量非负 D 发点流出的合流等于流入收点的合流8.下列正确的结论是A 最大流等于最大流量B 可行流是最大流当且仅当存在发点到收点的增广链C可行流是最大流当且仅当不存在发点到收点的增广链 D调整量等于增广链上点标号的最大值9.下列正确的结论是A 最大流量等于最大截量B 最大流量等于最小截量C 任意流量不小于最小截量D 最大流量不小于任意截量计算题6.1 求以下网络的最小支撑树和从节点1到节点12的最短路径。

运筹学1至6章习题参考答案第1章 线性规划1.1 工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1－23所示．310和130.试建立该问题的数学模型,使每月利润最大．【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量，则数学模型为123123123123123max 1014121.5 1.2425003 1.6 1.21400150250260310120130,,0Z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤≤⎪⎨≤≤⎪⎪≤≤⎪≥⎪⎩ 1.2 建筑公司需要用5m 长的塑钢材料制作A 、B 两种型号的窗架．两种窗架所需材料规格及数量如表1－24所示：【解设x j （j =1,2,…，10）为第j 种方案使用原材料的根数，则 （1）用料最少数学模型为10112342567368947910min 28002120026002239000,1,2,,10jj j Z x x x x x x x x x x x x x x x x x x j ==⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩∑ （2）余料最少数学模型为2345681012342567368947910min 0.50.50.52800212002*********0,1,2,,10j Z x x x x x x x x x x x x x x x x x x x x x x x x j =++++++⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩1.3某企业需要制定1～6月份产品A 的生产与销售计划。

已知产品A 每月底交货，市场需求没有限制，由于仓库容量有限，仓库最多库存产品A1000件，1月初仓库库存200件。

1～6月份产品A 的单件成本与售价如表1－25所示。

（2）当1月初库存量为零并且要求6月底需要库存200件时，模型如何变化。

运筹学知到章节测试答案智慧树2023年最新华东交通大学第一章测试1.用运筹学解决问题时，要对问题进行（）。

参考答案:分析和定义2.运筹学是一门（）。

参考答案:定量与定性相结合的学科3.规划论内容不包括（）。

参考答案:网络分析4.运筹学主要研究对象是各种有组织系统的管理问题及生产经营活动。

（）参考答案:对5.研究大量随机现象，从中揭示出事物基本规律的科学方法是指线性规划法。

（）参考答案:错6.统筹学是用教学方法研究各种系统最优化问题的学科。

（）参考答案:错7.若用图解法求解线性规划问题，则该问题所含决策变量的数目一般为（）。

参考答案:二个8.图解法求解极小化线性规划问题，一般目标函数直线放在可行域内，并（）移动。

参考答案:沿着梯度反方向移动。

9.在二元线性规划问题中，如果问题有可行解，则一定有最优解。

（）参考答案:错10.任何线性规划问题一定有最优解。

（）参考答案:错11.下面哪些不是线性规划问题的标准形式所具备的（）？参考答案:添加新变量时，可以不考虑变量的正负性12.线性规划标准型中，决策变量（）是非负的。

参考答案:一定13.下列哪种解法必须化标准型（）？参考答案:单纯形表格法14.线性规划的标准型主要特征为：(1)目标函数为极大化类型；(2)所有的约束条件都是等式；(3)所数学规划有约束方程右端的常数都是非负的；(4)所有决策变量都是非负的。

（）参考答案:对15.对于线性规划问题，下列说法正确的是（）。

参考答案:说法都正确16.对于任意线性规划问题（含三维以上），它的基可行解和可行域的顶点是一一对应的即基可行解数等于可行域的顶点数。

（）参考答案:对17.基可行解的分量都是正的。

（）参考答案:错18.如果线性规划问题存在最优解，则最优解一定可以在可行解域的顶点上获得。

（）参考答案:对19.可行解是满足约束条件和非负条件的决策变量的一组取值:（）参考答案:正确20.用单纯形法求解线性规划时，不论极大化或者是极小化问题，均用最小比值原则确定出基变量:（）参考答案:正确21.求极小值，唯一最优解情形，要求所有检验数（）时达到最优。

运筹学（第2版）习题答案第1章 线性规划 P36~40第2章 线性规划的对偶理论 P68~69 第3章 整数规划 P82~84 第4章 目标规划 P98~100第5章 运输与指派问题 P134~136 第6章 网络模型 P164~165 第7章 网络计划 P185~187 第8章 动态规划 P208~210 第9章 排队论 P239~240 第10章 存储论 P269~270 第11章 决策论 Pp297－298 第12章 博弈论 P325~326 全书360页习题一1.1 讨论下列问题：（1）在例1.2中，如果设x j (j=1，2，…，7)为工作了5天后星期一到星期日开始休息的营业员，该模型如何变化．（2）在例1.3中，能否将约束条件改为等式；如果要求余料最少，数学模型如何变化；简述板材下料的思路．（3）在例1.4中，若允许含有少量杂质，但杂质含量不超过1％，模型如何变化．（4）在例1.6中，假定同种设备的加工时间均匀分配到各台设备上，要求一种设备每台每天的加工时间不超过另一种设备任一台加工时间1小时，模型如何变化．(5)在单纯形法中，为什么说当00(1,2,,)k ik a i m λ>≤=并且时线性规划具有无界解。

1.2 工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1－23所示．310和130.试建立该问题的数学模型,使每月利润最大．【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量，则数学模型为123123123123123max 1014121.5 1.2425003 1.6 1.21400150250260310120130,,0Z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤≤⎪⎨≤≤⎪⎪≤≤⎪≥⎪⎩1.3 建筑公司需要用6m 长的塑钢材料制作A 、B 两种型号的窗架．两种窗架所需材料规格及数量如表1－24所示：【解】设x j （j =1,2,…，14）为第j 种方案使用原材料的根数，则 （1）用料最少数学模型为14112342567891036891112132347910121314min 2300322450232400232346000,1,2,,14jj j Z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x j ==⎧+++≥⎪++++++≥⎪⎪++++++≥⎨⎪++++++++≥⎪⎪≥=⎩∑ 用单纯形法求解得到两个基本最优解 X (1)=( 50 ,200 ,0 ,0,84 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=534 X (2)=( 0 ,200 ,100 ,0,84 ,0,0 ,0 ,0 ,0 ,0 ,150 ,0 ,0 );Z=534 （2）余料最少数学模型为134131412342567891036891112132347910121314min 0.60.30.70.40.82300322450232400232346000,1,2,,14j Z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x j =+++++⎧+++≥⎪++++++≥⎪⎪++++++≥⎨⎪++++++++≥⎪⎪≥=⎩ 用单纯形法求解得到两个基本最优解X (1)=( 0 ,300 ,0 ,0,50 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0，用料550根 X (2)=( 0 ,450 ,0 ,0,0 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0，用料650根 显然用料最少的方案最优。