下载文档原格式
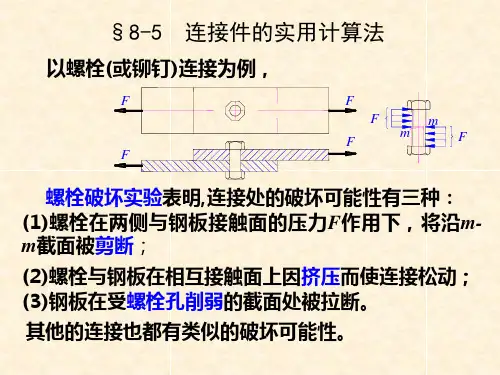
连接件受力经验计算公式
1. 螺栓连接
- 轴向受力:F=π/4*d^2*σ
其中,F为轴向受力(N),d为螺栓公称直径(mm),σ为许用应力(MPa)。
- 剪切受力:F=0.6*π/4*d^2*τ
其中,F为剪切受力(N),d为螺栓公称直径(mm),τ为许用剪切应力(MPa)。
2. 焊缝连接
- 角焊缝受力:F=0.707*l*a*τ
其中,F为受力(N),l为焊缝长度(mm),a为腿长(mm),τ为许用剪切应力(MPa)。
- 对接焊缝受力:F=π/4*d^2*σ
其中,F为受力(N),d为焊缝直径(mm),σ为许用拉伸应力(MPa)。
3. 键连接
- 平键受力:F=d*l*p*τ
其中,F为受力(N),d为键宽(mm),l为键长(mm),p为键高(mm),τ为许用剪切应力(MPa)。
- 垫圈受力:F=π/4*d^2*σ
其中,F为受力(N),d为垫圈外径(mm),σ为许用压力(MPa)。
4. 销连接
- 剪切受力:F=π/4*d^2*τ
其中,F为剪切受力(N),d为销直径(mm),τ为许用剪切应力(MPa)。
- 压力受力:F=d*l*p
其中,F为压力受力(N),d为销直径(mm),l为销长(mm),p为许用压力(MPa)。
以上公式是基于经验和理论推导得出的,在实际应用中还需要考虑各种安全系数、工艺条件和使用环境等因素,对计算结果进行适当调整。
同时,对于一些特殊情况或复杂载荷工况,可能需要采用有限元分析等更精确的计算方法。
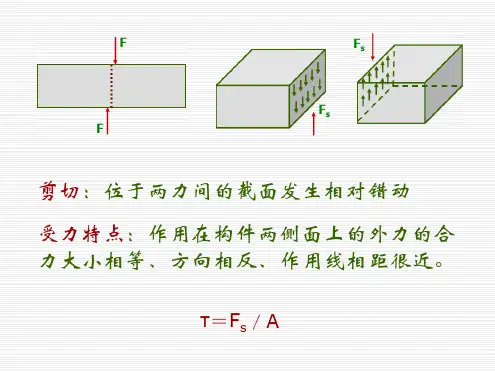
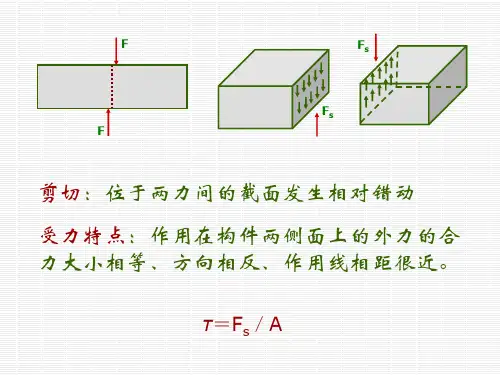
结合面摩擦系数是计算受到剪切方向载荷的螺栓连接非常重要的一个
参数，该数值取值大小会较大影响着螺栓选用的规格和性能等级。
对于紧固件连接的工程师来说，下面这个计算公式相信没有不熟悉的：
这个就是VDI2230标准的计算螺栓接头受到横向剪切方向载荷和扭转
载荷时计算所需的最小夹紧力的计算公式。
螺栓轴向力FKQ将两个或多个部件连接在一起，并通过结合面摩擦系
数μT产生的静摩擦力，用以传递螺栓切向载荷FQ或扭矩MY。
同样一个外部横向剪切方向的载荷10KN的接头，如果摩擦系数μTmin
取0.12,0.15,0.2,0.3计算出所需要的夹紧力会差别很大。
因此，有
必要对这个摩擦系数进行讨论。
我们常规计算中，一般取结合面摩擦系数为0.12，也有取0.15，这些
计算用的结合面摩擦系数从相关论文中也可以查出。
在汽车设计中，如果按照0.12,0.15的这些摩擦系数来计算校核接头
的所需夹紧力是否满足要求，往往发现所选用的螺栓规格较小，不能
满足外部载荷要求，特别是不能满足汽车滥用工况最大载荷情况下的
螺栓连接接头零件不能产生滑动的要求。
而这些车子都已经运行生产多年，没有大量出现因接头滑动的问题情况。
这说明设计的螺栓和拧紧要求是满足的。
因此，有必要怀疑常规
设计计算选用的摩擦系数选取0.12,0.15的合理性。
众所周知，电动车因为增加了电池包的重量，使整车的重量大大增加，以续航500km的电动车为例，往往比同等尺寸规格的燃油车重量要增
加300-400kg，也就是说有可能螺栓的规格会增大。
铆钉长度计算公式铆钉是一种在机械连接中常用的零件，它能够将两个或多个部件牢固地连接在一起。
而要确定合适的铆钉长度，就需要用到铆钉长度计算公式啦。
先来说说铆钉的作用吧。
想象一下，你有一个精致的小书架，板子和架子之间需要紧紧相连，这时候铆钉就派上用场了。
它就像一个小小的大力士，默默地在背后发力，让整个书架稳稳当当的。
那铆钉长度到底怎么算呢？其实铆钉长度的计算并不是一件特别复杂的事儿，但也需要我们认真对待。
一般来说，铆钉长度的计算公式是这样的：铆钉长度 = 被连接件总厚度 + 铆钉伸出长度。
这里的被连接件总厚度很好理解，就是需要连接的那些板子、零件啥的加在一起的厚度。
那铆钉伸出长度又是啥呢？这就有点讲究了。
通常情况下，铆钉伸出长度会根据不同的连接要求和材料有所变化。
比如说，在一些比较软的材料连接中，铆钉伸出长度可能相对短一点；而在硬度较高的材料连接时，铆钉伸出长度就要适当增加，以保证连接的牢固性。
我曾经在一个小车间里帮忙，当时师傅正在组装一批金属零件。
他拿着卡尺仔细地测量着被连接件的厚度，嘴里还念叨着铆钉长度的计算。
我在旁边好奇地看着，只见他熟练地运用公式，算出了合适的铆钉长度，然后拿起铆钉，用工具一敲，就稳稳地连接好了零件。
那一瞬间，我深刻地感受到了这个公式的实用和重要。
再来说说实际应用中的一些小技巧。
如果被连接件的表面不太平整，那在计算总厚度时，要多考虑一些余量，免得铆钉长度不够。
还有啊，如果是在振动比较大的环境中使用铆钉连接，也要适当增加铆钉长度，这样能更好地防止松动。
另外，不同类型的铆钉，其长度计算可能会有一些细微的差别。
比如抽芯铆钉和实心铆钉，在计算时就需要根据它们各自的特点进行调整。
总之，铆钉长度计算公式虽然看起来简单，但在实际应用中，需要我们结合具体情况，灵活运用，才能确保连接的质量和可靠性。
就像生活中的很多事情一样，看似简单的背后，往往需要我们用心去琢磨、去实践。
希望大家以后在遇到需要使用铆钉连接的时候，都能准确算出合适的铆钉长度，让工作和生活中的连接更加牢固、可靠！。
