当前位置：文档之家 › [题21]已知逻辑函数的真值表如表P21(a),(b),试写出对应的

[题21]已知逻辑函数的真值表如表P21(a),(b),试写出对应的

  • 格式：doc
  • 大小：147.00 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

数字电路与逻辑设计习题及参考答案

数字电路与逻辑设计习题及参考答案

数字电路与逻辑设计习题及参考答案一、选择题1. 以下表达式中符合逻辑运算法则的是 D 。

·C=C 2 +1=10 <1 +1=12. 一位十六进制数可以用 C 位二进制数来表示。

A . １ B . ２ C . ４ D . 163. 当逻辑函数有n 个变量时，共有 D 个变量取值组合？A. nB. 2nC. n 2D. 2n 4. 逻辑函数的表示方法中具有唯一性的是 A 。

A .真值表 B.表达式 C.逻辑图 D.状态图5. 在一个8位的存储单元中，能够存储的最大无符号整数是 D 。

A .（256）10 B .（127）10 C .（128）10 D .（255）106.逻辑函数F=B A A ⊕⊕)( = A 。

C.B A ⊕D. B A ⊕ 7．求一个逻辑函数F 的对偶式，不可将F 中的 B 。

A .“·”换成“+”，“+”换成“·” B.原变量换成反变量，反变量换成原变量 C.变量不变D.常数中“0”换成“1”，“1”换成“0” 8．A+BC= C 。

A .A+B +C C.（A+B ）（A+C ） +C9．在何种输入情况下，“与非”运算的结果是逻辑0。

DA ．全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是1 10．在何种输入情况下，“或非”运算的结果是逻辑1。

AA ．全部输入是0 B.全部输入是1 C.任一输入为0，其他输入为1 D.任一输入为111．十进制数25用8421BCD 码表示为 B 。

101 010112．不与十进制数（）10等值的数或代码为 C 。

A .(0101 8421BCD B .16 C .2 D .813．以下参数不是矩形脉冲信号的参数 D 。

A.周期 B.占空比 C.脉宽 D.扫描期 14．与八进制数8等值的数为： BA. 2B.16C. )16D. 215. 常用的BCD码有 D 。

A.奇偶校验码B.格雷码码 D.余三码16.下列式子中，不正确的是(B)+A=A B.A A1⊕=⊕=A ⊕=A17.下列选项中，______是TTLOC门的逻辑符号。

数字电子技术模拟试题及答案

数字电子技术模拟试题及答案

《数字电子技术》模拟试题 20分）一、填空题（每题2分，共 1511、十六进制数97 。

，对应的十进制数为 0 时，输出为2”描述的是与运算的规则。

、“至少有一个输入为 0 变量逻辑函数有16个最小项。

、 4 3 运算。

非和 4、基本逻辑运算有: 与、或加器。

半 5、两二进制数相加时，不考虑低位的进位信号是电平。

高 6、TTL器件输入脚悬空相当于输入线、地址线和控制线。

数据 7、RAM的三组信号线包括：位。

最高8、采用四位比较器对两个四位数比较时，先比较15分）二、单项选择题（每个3分，共的国标逻辑符号中是异或门。

B 1、图1图1C 。

2、下列逻辑函数表达式中可能存在竞争冒险的是B)(B?(A?C)F? B A )B?C)(?(A?BFF?(A?B)(B?C)F?(A?B)(B?C) D C3、下面逻辑式中，不正确的是_ A___。

ABC?A?B?C B. A. A??ABA D. C. AA??B)A(BAAB?4、时序逻辑电路中必须有___B___。

A. 输入逻辑变量B. 时钟信号C. 计数器D. 编码器5、有S1，S2两个状态，条件 B 可以确定S1和S2不等价。

A. 输出相同次态不同D. 次态相同C. 输出不同B.10分）三、简答题（共A??B左边＝（A?）（A?B）（?1A?A?B）?解：分） 1、（证明：4B?BA?A?A12、某逻辑函数的真值表如表所示，画出卡诺图。

（6分）某逻辑函数的真值表 1 表F B A C0 0 0 01 1 0 01 0 1 0X 1 1 0X 0 0 10 0 1 11 1 0 1X1 11分）四、分析题（20Z图2分析图2所示电路的逻辑功能。

1）列出其时钟方程：（2分） CP1＝CP↑；CP0＝CP↑。

2）列出其驱动方程：（4分）Q1；K0＝＝1 ；J0。

Q0J1＝；K1＝1?Q?Q1或XX3）列出其输出方程：（1分）Z＝XQ1Q0n?1n?1?QQ1Q0Q?Q1?Q0?XQ1或Q1?Q0?XQ1Q04）求次态方程：4（分）；10分）9）作状态表及状态图（5．五、波形题（10分）出图如3所示，试画的，入已知输信号XY，Z波形的波形。

逻辑函数的表示方法及转换

逻辑函数的表示方法及转换
求的真值表和逻辑表达式，画出实现的逻辑图
解：由逻辑要求写出真值表， 表2.5.6
如表2.5.6所示
输入
输出
A
B
C
Y
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
0
1
1
0
0
1
1
1
0
由真值表写出逻辑式为
表2.5.6
输入
输出
A
B
C
Y
Y ABC ABC ABC ABC 0
0
0
1
AB(C C) ABC ABC AB ABC ABC
如 Y＝A＋B C，表示输出等于变量B取反和变量C 的与，再和变量A相或。
2.5.2逻辑函数的几种表示方法 逻辑函数的表示方法很多，比较常用的如下：
一 、逻辑真值表
逻辑真值表就是采用 一种表格来表示逻辑函数的 运算关系，其中输入部分列 出输入逻辑变量的所有可能 取值得组合，输出部分根据 逻辑函数得到相应的输出逻 辑变量值。
A
输入
输出
O
t
A
B
Y
B
0
0
1
O Y
t
0
1
0
O 图2.5.6 例2.5.7的波形
t
1
0
0
1
1
1
由真值表可知，当输入变量A、B取值相同时，输出 Y＝1； A、B取值不同时，输出Y＝0。故输出和输 入是同或关系。其逻辑函数式为
Y AB AB
例2.5.8 已知图2.5. 7所示是某个数字逻辑电路的输入 输出波形，试画出该组合逻辑电路图，并判断其逻

逻辑函数化简题目

逻辑函数化简题目
= AB + AB ⋅ AB ⋅ C = AB + ( A + B)( A + B)C = AB + ABC + ABC
= AB(C + C ) + ABC + ABC = ABC + ABC + ABC + ABC
=m7+m6+m3+m5=∑m（3,5,6,7）
卡诺图简化法
例3 用卡诺图化简
F(A B,C, D =∑ (0,1 2,5, 6, 7,8,9,13 , ) m , ,14)
AC D
B C
BD
11
AC
F = AC+ AD+ B +B + ACD D C
AD
10
例10：某逻辑函数输入是8421 10：某逻辑函数输入是8421BCD码，其逻辑表达式为： 码 其逻辑表达式为： 8421 L（A,B,C,D）=∑ （1,4,5,6,7,9）+∑ （10,11,12,13,14,15） （ , ）=∑m（1,4,5,6,7,9）+∑d（10,11,12,13,14,15） 用卡诺图法化简该逻辑函数。 用卡诺图法化简该逻辑函数。 画出4变量卡诺图。 号小方格填入1 解：（1）画出4变量卡诺图。将1、4、5、6、7、9号小方格填入1； 10、11、12、13、14、15号小方格填入 号小方格填入× 将10、11、12、13、14、15号小方格填入×。 合并最小项，如图（ ）所示。注意， 方格不能漏。 （2）合并最小项，如图（a）所示。注意，1方格不能漏。×方格 根据需要，可以圈入，也可以放弃。 根据需要，可以圈入，也可以放弃。 写出逻辑函数的最简与—或表达式 或表达式: （3）写出逻辑函数的最简与 或表达式: 如果不考虑无关项，如图（b）所示，写出表达式为： 如果不考虑无关项，如图（b）所示，写出表达式为：

真值表_精品文档

真值表_精品文档

真值表什么是真值表？真值表是数理逻辑中的一种重要工具，用于展示或描述一个命题逻辑公式的所有可能的输入真值情况下的输出结果。

它可以直观地展示逻辑表达式的真假变化，并帮助我们理解和分析复杂的逻辑关系。

在计算机科学、数字电路设计和人工智能等领域，真值表也被广泛应用。

真值表的构成一个简单的真值表由多个列组成，每一列代表一个命题变量，最后一列代表整个命题逻辑公式的输出结果。

真值表的行数由命题变量的个数决定，每一行代表一种命题变量的真假组合。

对于n个命题变量的真值表，共有2^n 行。

真值表最常用的列数为n+1，其中n为命题变量的个数。

在真值表中，每个命题变量都有两种可能的取值，分别为真（1）和假（0）。

输出结果也只有两种情况，即真（1）和假（0）。

真值表的示例以下是一个简单的真值表示例，假设我们有两个命题变量A和B：A B A AND B0 0 00 1 01 0 01 1 1这个示例真值表展示了两个命题变量A和B进行逻辑与（AND）运算的结果。

可以看出，只有当A和B都为真时，A AND B 才为真，否则为假。

这符合逻辑与运算的规则。

另一个常见的逻辑运算是逻辑或（OR）运算，下面是一个两个命题变量A和B 的逻辑或运算的真值表示例：A B A OR B0 0 00 1 11 0 11 1 1可以观察到，只有当A和B中至少一个为真时，A OR B 才为真。

这也符合逻辑或运算的规则。

当命题变量的个数增加时，真值表会变得更大和更复杂。

但是，无论多少个命题变量，真值表的基本结构和原理都是一样的。

真值表的应用真值表作为一种逻辑工具，在计算机科学、数字电路设计和人工智能等领域有着广泛的应用。

在计算机科学中，真值表可以用于验证和分析布尔代数表达式、逻辑电路电路设计以及计算机程序的逻辑正确性。

通过对真值表的分析和推导，我们可以确保我们的程序在各种输入情况下都能得到正确的输出。

在数字电路设计中，真值表可以帮助设计师分析和优化逻辑电路的功能和性能。

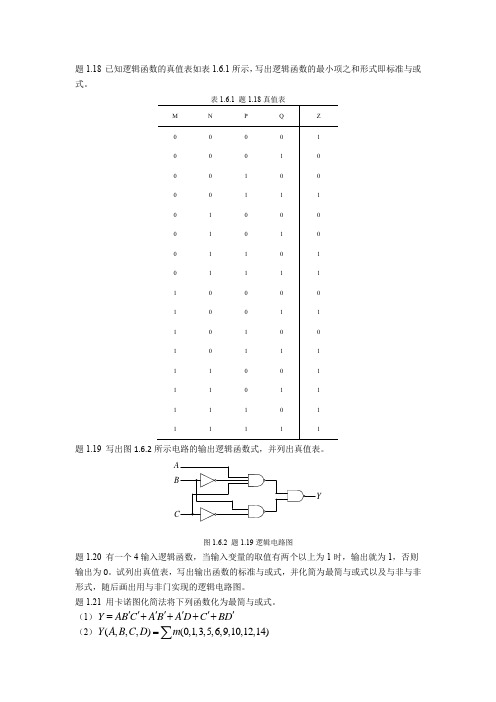
第一章作业2

第一章作业2

题1.18已知逻辑函数的真值表如表1.6.1所示，写出逻辑函数的最小项之和形式即标准与或式。

表1.6.1题1.18真值表题1.19写出图1.6.2所示电路的输出逻辑函数式，并列出真值表。

图1.6.2 题1.19逻辑电路图题1.20有一个4输入逻辑函数，当输入变量的取值有两个以上为1时，输出就为1，否则输出为0。

试列出真值表，写出输出函数的标准与或式，并化简为最简与或式以及与非与非形式，随后画出用与非门实现的逻辑电路图。

题1.21用卡诺图化简法将下列函数化为最简与或式。

（1）Y AB C A B A D C BD '''''''=++++ （2）(,,,)(0,1,3,5,6,9,10,12,14)Y A B C D m =∑（3）2()Y C D A B A BC A C D ''''''=⊕++给定约束条件为0AB CD += ( 4)2(,,,)(3,5,6,7,9)(0,1,2,4,8)Y A B C D m d =+∑选作题：来源于往届期末考试题 1． 8421BCD 码共有状态。

（A ）8 （B ）10（C ）12（D ）162. 连续同或1985个1的结果是什么? 单数个1连续同或、双数个1连续同或的结果各是什么？3. 图2（b ）是一组合电路。

问：图2（b ）的二进制输入S 3S 2S 1S 0是什么码时，输出F 为1？已知输入C 为0。

4. 任意项和约束项有微小的区别，区别在于任意项值，约束项值。

约束项和任意项统称为。

（A ）随便（B ）不允许（C ）无关（D ）最高 5．有三个逻辑变量A 、B 、C ，它们分别表示一台电动机的正转、反转和停止的命令，A=1表示正转，B=1表示反转，C=1表示停止。

电动机任何时候只能执行一个命令，请写出描述上述情况的约束项逻辑表达式。

6．卡诺图中的逻辑相邻或对称相邻具有特征，其数值不同只是在某位上差位。

数电期中考试试卷答案

1、逻辑代数基础（15分，每题5分）（1A B C Y0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 1111CBACBACBAY++=（2）用卡诺图化简法将下列函数化为最简与或形式。

DCBCCABAY++++=DCBAY++=（3）将下列各函数式化为最小项之和的形式。

CBACBCAY++=CBAABCCBABCAY+++=2 逻辑门电路（10分，每题2分）（1）．电路如图（a），（b）所示，设开关闭合为1、断开为0；灯亮为1、灯灭为0。

F对开关A、B、CEA BCRF1E CABF2(a)(b)Ａ．C AB F =1 )(2B A C F += Ｂ．C AB F =1 )(2B A C F +=Ｃ． C B A F =2 )(2B A C F += （２）．某TTL 反相器的主要参数为I IH ＝20μA ；I IL ＝1.4ｍA ；I OH ＝400μA ； I OL ＝14ｍA ，带同样的门数（ ）。

Ａ．２０ Ｂ．２００ Ｃ．１０ Ｄ．１００ （３）在TTL 门电路的一个输入端与地之间开路，则相当于在该输入端输入（ ）。

A ．高阻态B ．高电平C ．低电平 （４）．在 正 逻 辑 条 件 下， 如 图 所 示 逻 辑 电 路 为( ) 。

A ．“ 与 ” 门 B ．“ 或” 门 C ．“ 非” 门D ．“ 与非” 门+12VABFR（5）．CMOS 门 电 路 的 扇 出 系 数 比 TTL 门 电 路( )。

(a) 小 得 多 (b) 小 (c) 大 得 多 １．Ａ ２．Ｃ ３．Ｂ ４．Ａ 5．Ｃ3、组合逻辑电路（40分，每题10分）(1) 有一水箱由大、小两台泵M L 和M S 供水，如图P3.4所示。

水箱中设置了3个水位检测元件A 、B 、C 。

水面低于检测元件时，检测元件给出高电平；水面高于检测元件时，检测元件给出低电平。

现要求当水位超过C 点时水泵停止工作；水位低于C 点而高于B 点时M S 单独工作；水位低于B 点而高于A 点时M L 单独工作；水位低于A 点时M L 和M S 同时工作。

数字电子技术基础(数电)课后习题解答

题1.1 完成下面的数值转换： （1）将二进制数转换成等效的十进制数、八进制数、十六进制数。 ①（0011101）2 ②（11011.110）2 ③（110110111）2
解： ① （0011101）2 =1×24+ 1×23+ 1×22+ 1×20=(29)10
（0011101）2 =(0 011 101)2= (35)8 （0011101）2 =(0001 1101)2= (1D)16 同理：② (27.75)10，(33.6)8，(1B.C)16； ③ (439)10，(667)8，(1B7)16；
(1) Y=AB+BC+A'C'
=B+A'C'
BC
A
00 01 11 10
0
1
11
1
11
(2) Y=AB'C'+A'B'+A'D+C+BD =B’+C+D (或用圈0法）
CD 00 01 11 10
AB
00 1
1
1
1
01
1
1
1
11
1
1
1
10 1
1
1
1
(3) Y=A' (B'C+B(CD'+D))+ABC'D
1
010
1
011
1
100
1
101
1
110
1
111
0
题1.9 在举重比赛中，有甲、乙、丙三名裁判，其中甲为主裁判，乙、丙为副裁判，当主裁判 和一名以上（包括一名）副裁判认为运动员上举合格后，才可发出合格信号。列出该函数的 真值表。

第3章 逻辑代数基础-习题答案

（5） AB + B(C + D) 解： = (A + B + D)(A + B + C) = (A + B + D) + (A + B + C) （6） ABD + ACD + CD + ABC + ACD 解： = (A + D)(A + B + C + D) = (A + D) + (A + B + C + D)
使函数为 0 的组合即最大项，有 ABCD=“0000”，“0010”，“0011”，“0100”，“1000”，“1001”,“1010”， “1110”；使之为 1 的逻辑变量组合有 ABCD=“0001”，“0101”，“0110”，“0111”，“1011”，“1100”，“1101”， “1111”。 （3） X = AC + AB + BCD + BD + ABD + ABCD
X BCD AC D A C D A B D
ABCD ABCD ABC D AB C D ABC D A B C D A BC D
(0, 2, 4,7,8,12,15) (1,3,5,6,9,10,11,13,14)
3.3 分别指出下列逻辑函数的所有最大项和所有最小项，并说明哪些变量组合使得函数为 0，哪些变 量组合使得函数为 1。
=(B + D)(A+ D)C = (AB + AD + BD)C = (AD + BD)C = ACD + BC D
（4） C D + A + CD + AB 解： C D A+CD+ AB = AC + AD +CD+ AB

第二章习题

《数字电子技术》第二章作业题
批次课程：班级：姓名：学号：
2.1 证明下列逻辑恒等式。

（1）AB′+B+A′B=A+B
（2）（A+C′）（B+D）（B+D′）=AB+BC′
2.2 已知逻辑函数的真值表如表所示，试写出Y的逻辑表达式。

2.3列出下列函数的真值表。

Y=A′B+BC+ACD′
2.4 将下列各函数化为最小项之和的形式。

（1）Y=A′BC+AC+B′C
（2）Y=AB′C′D+BCD+A′D
2.5 用逻辑代数的基本公式和常用公式将下列逻辑函数式化为最简与或形式。

（1）Y=AC′+ABC+ACD′+CD
（2）Y=BC′+ABC′E+B′(A′D′+AD) ′+B(AD′+A′D)
2.6用卡诺图将下列函数化为最简与或表达式的形式。

（1）Y=AB′+A′C+BC+C′D
（2）Y(A,B,C)=Σm(0,1,2,5,6,7)
（3）Y(A,B,C,D)=Σm(0,1,2,5,8,9,10,12,14)
2.7用卡诺图将下列具有约束项的逻辑函数化为最简与或形式。

（1）Y=CD′(A⊕B)+A′BC′+A′C′D，给定约束条件为AB+CD=0 （2）Y(A,B,C)= Σm(1,2,4,7)+d(3,6)
（3）Y(A,B,C,D)=Σm(2,3,7,8,11, 14)+ d(0,5,10,15)。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

[题2.1]已知逻辑函数的真值表如表P2.1(a),(b)，试写出对应的逻辑函数式
[ 2.2]试用列真值表的方法证明下列异或运算公式。

(1)A⊕0=A (2) A⊕A=0 (3) A⊕A=1
(4)（A⊕B）⊕C=A⊕（B⊕C）
(5) A⊕1
A
B
B
=B
A
⊕
⊕
=
⊕
[题2.3] 用逻辑代数的基本公式和常用的公式将下列逻辑函数化为最简与或形式的。

（1）B
+
=
Y+
B
A
A
B
(2) B A
Y+
=
A
BC
（3）D
A
Y+
=
B
+
CD
A
C
ABD
（4）)
A
Y+
B
+
=
A
+
)(
A
(B
C
B
AD
CD
（5）)()(CE AD B BC B A D C AC Y ++++=
（6）))()((C B A C B A C B A Y ++++++=
（7）F E AB E D C B E D C B E D B F E B A D C A AC Y +++⊕+++=)(
[题2.4]写出图P2.4中各逻辑图的逻辑函数式，并化简为最简与或式。

[题2.5 ]求下列函数的反函数并化为最简与或形式。

（1）Y=AB+C (2) BC AC C A B A Y +++=))((
（3）（4）)(BD AC D C C B A Y ++=
（4）EFG G EF G F E G F E FG E G F E G F E G F E Y +++++++=
[题2.6]将下列各函数式化为最小项之和的形式。

(1) C B AC BC A Y ++=
（2）D A BCD D C B A Y ++=
（3）)(D C BC AB Y ++=
[题2.7] 将下列各式化为最大项之积的形式。

（1）))((C B A B A Y +++= （2）C B A Y +=
（3）∑=)7,6,4,2,1(),,(m C B A Y
图P2.4
[题2.8]用卡诺图化简法将下列函数化为最简与或形。

（1）D C A D C A C B A D C ABD ABC Y +++++=
（2）ABC B A C B B A Y ++++=
（3）C B AC B A Y ++=
（4）∑==)7,6,5,2,1,0(),,(m C B A Y
（5）∑=)14,11,10,9,8,6,4,3,2,1,0(),,,(D C B A Y
（6）∑=)14,12,10,9,8,5,2,1,0(),,,(m D C B A Y
[题2.9] 化简下列逻辑函数（方法不限
（1） Y=A B +A C+D C +D
（2） D C A D C A D C B D C D C A Y ++++=)(
（3） ))((D B C B A CD B D C B A D B A Y +++++=
[题2.10] 证明下列恒等式。

(1) C B AB D B D B C A +=+++))()((
(2) D B D B C A C A ABCD D C B A D C B A D C B A +++=+++
[题2.11] 试画出与非门和反相器实现下列函数
(1) Y=AB+BC+AC
(2) BC A C B A C AB Y ++=
[题2.12] 试画出用或非门和反相器实现下列函数的逻辑图。

(1)C B C B A Y += (2) D B A D D B C AB Y ++=)(
[题2.13]对相互排斥的一组变量A 、B 、C 、D 、E （任何情况下不可能有两个或两个以上同时为1），证明 E E D C B A D E D C B A C E D C B A B E D C B A A E D C B A =====,,,,
[题2.14]将下列函数化为最简与或函数式。

（1）D C B A D C B A D C A Y ++++=，给定约束条件为
0=+++++ABCD D ABC D C AB D C AB CD B A D C B A
（2）))(D C A C B A B A D C Y ++⊕=，给定约束条件为AB +CD =0
（3）),,,,(),,,(107653m m m m m D C B A Y ∑=给定约束条件是
084210=++++m m m m m
（4）∑=),,,,,(),,,(14118732m m m m m m D C B A Y ，给定约束条件为 0151050=+++m m m m。