第五届全国中学生数理化学科能力展示活动七年级数学解题技能展示试题及解答

第十届全国中学生数理化学科能力展示活动七年级数学解题技能展示试题(A卷)赛区㊀学校㊀㊀姓名㊀准考证号考生须知:１．请在答题纸和试卷上填写有效信息;２．考生必须在答题纸上答卷,否则成绩无效;３．考试时间为１２０分钟,满分１２０分．４．成绩查询:２０１８年１月５日起,考生可通过 中学生核心素养展示平台 (w w w．i s u y a n g．c n)查询自己的分数及获奖情况．一㊁选择题(每题６分,共４８分,每题只有１个选项是正确的)１．某市一年中各月平均最高气温和平均最低气温的雷达图(如右图)．图中点A表示１０月的平均最高气温约为１５ħ,点B表示４月的平均最低气温约为５ħ．下面叙述不正确的是(㊀㊀)．A㊀各月的平均最低气温都在０ħ以上;B㊀７月的平均温差比１月的平均温差大;C㊀平均最高气温高于２０ħ的月份有５个;D㊀３月和１１月的平均最高气温基本相同２．小明㊁小红㊁小刚㊁小丽四位同学向老师询问 第十届全国中学生数理化学科能力展示活动 的考场安排．老师说:你们４人中有２人在本校考㊁２人在外校考,然后老师给小明看了小红㊁小刚的考场;给小红看了小刚的考场;给小丽看了小明的考场．然后小明对大家说:我还是不知道我的考场．根据以上信息,则(㊀㊀)．A㊀小红可以知道４人的考场;B㊀小丽可以知道４人的考场;C㊀小红㊁小丽可以知道对方的考场;D㊀小红㊁小丽可以知道自己的考场３．某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况．加油时间加油量/L加油时的累计里程/k m２０１７年１０月１日１２３５０００２０１７年１０月１５日４８３５６００㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀注: 累计里程 指汽车从出厂开始累计行驶的路程．在这段时间内,该车每１００k m平均耗油量为(㊀㊀)．A㊀６升;㊀㊀B㊀８升;㊀㊀C㊀１０升;㊀㊀D㊀１２升４．Ac e r t a i n c a l c u l a t o r h a s o n l y t w ok e y s[＋１]a n d[ˑ２]．W h e n y o u p r e s s o n e o f t h e k e y s, t h ec a l c u l a t o ra u t o m a t i c a l l y d i s p l a y st h er e s u l t．F o ri n s t a n c e,i ft h ec a l c u l a t o ro r i g i n a l l y d i s p l a y e d ９ a n d y o u p r e s s e d[＋１],i tw o u l dd i s p l a y １０． I f y o ut h e n p r e s s e d[ˑ２],i t w o u l dd i s p l a y ２０． S t a r t i n g w i t h t h e d i s p l a y １, w h a t i s t h e f e w e s t n u m b e r o f k e y s t r o k e s y o uw o u l dn e e d t o r e a c h ２００ (㊀㊀)．A㊀８;㊀㊀B㊀９;㊀㊀C㊀１０;㊀㊀D㊀１１５．从数轴上单位长度线段开始,取走其中间１/３而达到第一阶段;然后从每一个余下的１/３线段中取走其中间１/３而达到第二阶段．无限地重复这一过程,余下的无穷点集就称为 康托尔集 ．右图是 康托尔集 的最初几个阶段,当达到第八个阶段时,余下的所有线段的长度之和为(㊀㊀)．A㊀(２３)２;㊀㊀B㊀(２３)６;㊀㊀C㊀(２３)８;㊀㊀D㊀(２３)１０６．陈老师要为他家的矩形餐厅(如右图)选择一张餐桌,并且想按如下要求摆放:餐桌一侧靠墙,靠墙对面的桌边留出宽度不小于８０c m的通道,另两边各留出宽度不小于６０c m的通道．那么在下面四张餐桌中,其大小规格符合要求的餐桌编号是(㊀㊀)．A㊀①②④;㊀㊀B㊀②④;㊀㊀C㊀①③;㊀㊀D㊀①②③④７．一个纸环链,纸环按红黄绿蓝紫的顺序重复排列,截去其中的一部分,剩下部分如右图所示,则被截去部分纸环的个数可能是(㊀㊀)．A㊀２０１８;㊀㊀B ㊀２０１７;㊀㊀C ㊀２０１６;㊀㊀D㊀２０１５８．给出以下数对序列:(１,１)(１,２)(２,１)(１,３)(２,２)(３,１)(１,４)(２,３)(３,２)(４,１) 记第i 行的第j 个数对为a i j ,如a ４３＝(３,２),则a n m ＝(㊀㊀)．A㊀(m ,n －m ＋１);㊀㊀㊀B ㊀(m －１,n －m );C ㊀(m －１,n －m ＋１);D㊀(m ,n －m )二、填空题(每题８分,共３２分)９．规定:l o g a b (a ＞０,a ʂ１,b ＞０)表示a ,b 之间的一种运算．现有如下的运算法则:l o g n n a ＝a ;l o g N M ＝l o g n M l o g n N (n ＞０,n ʂ１,N ＞０,N ʂ１,M ＞０)．例如:l o g ２２３＝３,l o g ２５＝l o g １０５l o g １０２,则l o g １００１０００＝．１０．填在下面各正方形中的四个数之间都有一定的规律,按此规律得出a ＋b ＋c ＝．１１．瑞典皇家科学院宣布将２０１７年度诺贝尔物理学奖授予美国的R a i n e r W e i s s ㊁K i p S ．T h o r n e 和B a r r y C ．B a r i s h ,用以表彰他们在引力波研究方面的贡献．这次探测到的引力波是两个黑洞在互相融合期间释放出的,这次的融合发生在１３亿年前,之后它们发出的引力波就开始向着包括地球在内的宇宙各个地方进行传播．若将一百万千米作为一个计数单位,则用科学计数法表示黑洞融合的位置距离地球有个计数单位．(已知引力波的传播速度是３ˑ１０８m /s ,小数点后保留２位有效数字,１年按３６５天计算)１２．对于任意的２个实数对(a ,b )和(c ,d ),规定:(a ,b )＝(c ,d ),当且仅当a ＝c ,b ＝d ;运算 ☉ 为(a ,b )☉(c ,d )＝(a c －b d ,b c ＋a d );运算 ⊕ 为:(a ,b )⊕(c ,d )＝(a ＋c ,b ＋d )．设p ,q ɪR ,若(１,２)☉(p ,q )＝(５,０),则(１,２)⊕(p ,q )的值为．三、解答题(本题共３小题,共４０分)１３．(１３分)运输一批海鲜,可在汽车㊁火车㊁飞机三种运输工具中选择,它们的速度分别为v㊁２v㊁１０v k m/h,每千米的运费分别为a㊁b㊁c元,且b＜a＜c,又这批海鲜在运输过程中的损耗为m元/h,若使用三种运输工具分别运输时各自的总费用(运费与损耗之和)互不相等,试确定使用哪种运输工具总费用最省．(题中字母均为正的已知量)１４．(１３分)有理数a㊁b㊁c均不为零,且a＋b＋c＝０．设x＝|a|b＋c＋|b|c＋a＋|c|a＋b,试求代数式x１９－２０１７x＋２０１７的值．１５．(１４分)某人租用一辆汽车由A城前往B城,沿途可能经过的城市以及通过两城市之间所需的时间(单位:小时)如图所示,若汽车行驶的平均速度为８０k m/h,而汽车每行驶１k m需要的平均费用为１ ２元．请指出此人从A城出发到B城的最短路线(要有推理过程),并求出所需费用最少为多少元?。

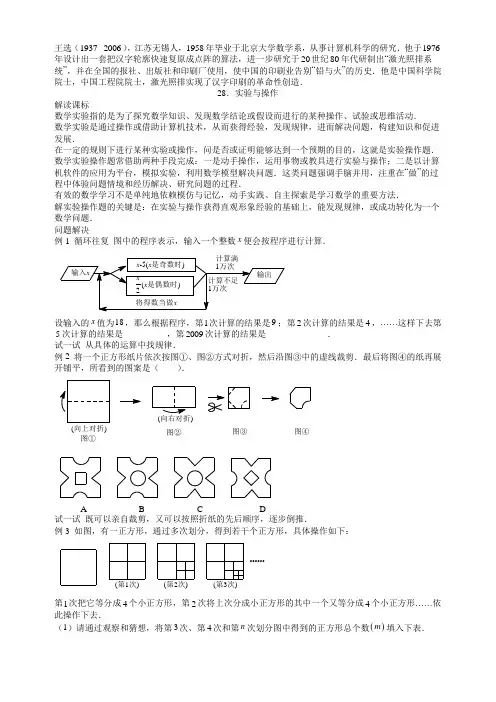
王选（1937-2006），江苏无锡人，1958年毕业于北京大学数学系，从事计算机科学的研究．他于1976年设计出一套把汉字轮廓快速复原成点阵的算法，进一步研究于20世纪80年代研制出“激光照排系统”，并在全国的报社、出版社和印刷厂使用，使中国的印刷业告别“铅与火”的历史．他是中国科学院院士，中国工程院院士，激光照排实现了汉字印刷的革命性创造．28．实验与操作解读课标数学实验指的是为了探究数学知识、发现数学结论或假设而进行的某种操作、试验或思维活动． 数学实验是通过操作或借助计算机技术，从而获得经验，发现规律，进而解决问题，构建知识和促进发展．在一定的规则下进行某种实验或操作，问是否或证明能够达到一个预期的目的，这就是实验操作题． 数学实验操作题常借助两种手段完成：一是动手操作，运用事物或教具进行实验与操作；二是以计算机软件的应用为平台，模拟实验，利用数学模型解决问题．这类问题强调手脑并用，注重在“做”的过程中体验问题情境和经历解决、研究问题的过程．有效的数学学习不是单纯地依赖模仿与记忆，动手实践、自主探索是学习数学的重要方法．解实验操作题的关键是：在实验与操作获得直观形象经验的基础上，能发现规律，或成功转化为一个数学问题． 问题解决例1 循环往复 图中的程序表示，输入一个整数x 便会按程序进行计算．设输入的x 值为18，那么根据程序，第1次计算的结果是9；第2次计算的结果是4，……这样下去第5次计算的结果是__________，第2009次计算的结果是______________． 试一试 从具体的运算中找规律．例2 将一个正方形纸片依次按图①、图②方式对折，然后沿图③中的虚线裁剪．最后将图④的纸再展开铺平，所看到的图案是（ ）．图①向上对折()图②图③图④A B CD试一试 既可以亲自裁剪，又可以按照折纸的先后顺序，逐步倒推．例3 如图，有一正方形，通过多次划分，得到若干个正方形，具体操作如下：第1次()第2次()第3次()第1次把它等分成4个小正方形，第2次将上次分成小正方形的其中一个又等分成4个小正方形……依此操作下去．（1）请通过观察和猜想，将第3次、第4次和第n 次划分图中得到的正方形总个数()m 填入下表．试一试略例4 有1997枚硬币，其中1000枚国徽朝上，997枚国徽朝下．现在要求每一次翻转其中任意6枚，使它们的国徽朝向相反．问：能否经过有限次翻转后，使所有硬币的国徽都朝上？给出你的结论，并给出证明．试一试国徽朝上朝下具有相反意义，将国徽朝上赋值“1-”．这样，若干枚国徽的朝+”，朝下赋值“1向情况可用若干个数的乘积来表示，把一个实际操作题转化为一个数学问题．例5 在22⨯方格纸中，以格点连线为边作面积为2的多边形（含凹多边形），请尽可能多地找出答案，在寻找答案的过程中你能发现什么规律吗？分析与解若没有规律性的认识，则要无遗漏重复地找出全部解答是困难的．恰当的方法是：选择一些图形作基本图形，通过基本图形的组合找出解答，可将下列7个图形作为基本图形：1()2()3()4()5()6()7()由此可得如下23个解答，其中凸多边形7个，凹多边形16个：1()2()3()4()5()6()7()8()()15()16()()14()13()119()10()12()23()()21()21()18()20()1917俄罗斯方块例6 游戏机的“方块”中共有下面7种图形，每种“方块”都由4个11⨯的小方格组成．现用这7种图形拼⨯的长方形（可以重复使用某些图形）．问：最多可以用这7种图形中的几种图形？成一个74⨯的长方形的28个小方格黑白相间染色，除“品”字形必占3个分析与解为了形象化地说明问题，对74黑格1个白格或3个白格1个黑格外，其余6个方块各占2个黑格2个白格．⨯的长方形，方法很多，如图①仅出示一种．用其中的6种不同的图形方块可以拼成74⨯的长方形的28个小方格黑白相间染色，则如图②所示，下面证明不能7种图形方块都各用一次，将74⨯的长方形能用7种不同的方块拼成，则每个方块用到一次且只用一次．其中黑、白格各14个，若74“品”字形如图③必占3个黑格1个白格或3个白格1个黑格，其余6个方块各占2个黑格2个白格．7种不同的方块占据的黑格总数、白格总数都是奇数个，不会等于14．矛盾．因此，不存在7种图形方块⨯的长方形的方法．每个各用一次拼成74所出，要拼成74⨯的长方形，最多可以用这7种图形方块中的6种．图③数学冲浪知识技能广场1．乐在其中七巧板的起源要追溯到我国先秦时期，古算书《周髀算经》中即有正方形分割术，经历代演变而成“七巧图”（又称为“益智图”和“智慧板”，如图①）．19世纪传到国外，多称其为“唐图”（意为“来自中国的拼图”），引起人们的极大兴趣，欧美许多国家纷纷出版书籍予以介绍．图①图②如果有一副七巧板的总面积是100平方厘米，那么其中正方形的那一块的面积是________平方厘米．图②“乐在其中”的每个字都是由一副七巧板摆拼所得，请在图中用线段画出模块之间的“拼缝”．2．如图，在33⨯的正方形网格中，已有两个小正方形被涂黑，再将图中其余小正方形任意涂黑一个，使整个图案构成一个轴对称图形的方法有________种．3．如图，将长度为20cm，宽为2cm的长方形的纸带，折成如图所示的图形并在其一面着色，则着色部分的面积为___________2cm．4．定义一种对正整数n的“F”运算：①当n为奇数时，结果为35n+；②当n为偶数时，结果为2kn（其中k是使2kn为奇数的正整数），并且运算重复进行．例如：取26n=，则26134411F F F−−−→−−−→−−−→第一次第二次第三次②①②若449n=，则第449次“F”运算的结果是____________．5．图中的大正三角形是由9个相同的小正三角形拼成的，将其部分涂黑，如图①、②所示．观察图①、图②中涂黑部分构成的图案．它们具有如下特征：①都是轴对称图形，②涂黑部分都是三个小正三角形．请在图③、图④内分别设计一个新图案，使图案具有上述两个特征．图①图②图③图④思维方法天地6．折折剪剪一张正方形纸片，通过两次对折，然后按阴影部分进行裁剪并展开，可以得到如图（1）末的“蝴蝶结”：①裁剪并展开请你仿图①，将下面的正方形纸片经过两次对折后裁剪并展开，得到如图②末的图形，请画出虚线和实线表示折叠过程，并用阴影表示剪去的部分．②7．把四个完全相同的空啤酒瓶放置在桌面上，使得四个啤酒瓶底中心的距离两两相等．请写出摆法关键步骤（可画图辅助说明）：_________________________________________________________________________8．方格纸上有3个图形，你能沿着格线把每一个图形都分成完全相同的两个部分吗？9．有依次排列的3个数：3，9，8．对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，1-，8，这称为第一次操作；做第二次同样的操作后也可产生一个新数串：3，3，6，3，9，10-，1-，9，8．继续依次操作下去．问：从数串3，9，8开始操作至第100次以后所产生的那个新数串的所有数之和是多少？10．有三堆石子的个数分别是19，8，9，现在进行如下的操作：每次从这三堆石子中的任意两堆中各取出1个石子，然后把这2个石子都加到另一堆中去，试问能否经过若干次这样的操作后，使得：（1）三堆石子的数分别是2，12，22；（2）三堆都是12．如能，请用最快的操作完成；不能，则说明理由[注：若从第一、二堆各取1个到第三堆，可表示为()()19,8,918,7,11⇒等]．11．如图a 所示的展览馆有36个陈列室，每两个相邻陈列室之间有门可通，其入口与出口位置如图b 所示，现有人希望每个陈列室都能参观，但只经过每个展室一次，这可能吗？如果可能，请为他设计一条参观路线；如不可能，请说明理由．a入口展览大厅b进口出口应用探究乐园12．如图是一张“35⨯”（表示边长分别为3和5）的长方形，现要把它分成若干张边长为整数的长方形（包括正方形）纸片，并要求分得的任何两张纸片都不完全相同．（1）能否分成5张满足上述条件的纸片？ （2）能否分成6张满足上述条件的纸片？若能分，用“a b ⨯”的形式分别表示出各张纸片的边长，并画出分割的示意图；若不能分，请说明理由．13．图形的操作过程（本题中四个矩形的水平方向的边长均为a ，竖直方向的边长均为b ） 在图①中，将线段12A A 向右平移1个单位到12B B ，得到封闭图形1221A A B B ，（即阴影部分）；在图②中，将折线123A A A 向右平移1个单位到123B B B ，得到封闭图形123321A A A B B B （即阴影部分）． （1）在图③中，请你类似地画一条有两个折点的折线，同样向右平移1个单位，从而得到一个封闭图形，并用斜线画出阴影；（2）请你分别写出上述三个图形中除去阴影部分后剩余部分的面积： 1S =_________，2S =__________，3S =_____________； （3）联想与探索：如图④，在一块矩形草地上，有一条弯曲的柏油小路（小路任何地方的水平宽度都是1个单位），请你猜想空白部分表示的草地面积是多少？并说明你的猜想是正确的．图①22图②33图③图④微探究设而不求字母示数是代数的一个重要特征，是由算术跨越到代数的桥梁，是数学发展史上的一个飞跃． 字母示数具有简明性、一般性，在求代数式的值、形成公式、解应用题等方面有广泛的应用．为了沟通数量间的关系，或将有些不明朗的关系表示出来，我们需要设元，而所设的字母不能或不需要求出，这就是设而不求的基本涵义．例1 老师报出一个5位数，同学们将它的顺序倒排后得到的5位数减去原数，甲、乙、丙、丁的结果分别是34567，34056，23456，34956，老师判定4个结果中只有1个正确，答对的是________．试一试 设原数为abcde ，化简并判断e abcde dcba -的特征．例2 某大型超市从生产基地购进一批水果，运输过程中质量损失10%．假设不计超市其他费用，如果超市要想获得20%的利润，那么这种水果的售价在进价基础上应至少提高（ ）． A ．40% B ．33.4% C ．33.3% D ．30% 试一试 若要表示利润，则需指明质量、进价．例3 某地区民用电，按白天时段和晚间时段规定了不同的单价．某户8月份白天时段用电量比晚间时段用电量多50%，9月份白天时段用电量比8月份白天时段用电量少60%，结果9月份的用电量虽比8月份的用电量多20%，但9月份的电费却比8月份的电费少10%．求该地区晚间时段民用电的单价比白天时段的单价低的百分数．试一试 本例数量关系复杂，既涉及白天与晚间用电量的关系，不同月份用电量的关系，又关联月份间的电费，故要全面增设未知数．例4 从两个重量分别为12千克和8千克，且含铜的百分数不同的合金上切下重量相等的两块，把所切下的每块和另一块剩余的合金放在一起，熔炼后两个合金含铜的百分数相等．求所切下的合金的重量是多少千克？试一试 由于已知条件中涉及合金中含铜的百分数，因此只有增设这两个合金含铜的百分数为参数或与合金含铜的百分数有关的其他量为参数，才能充分利用已知，为列方程创造条件．例5 能否找到7个整数，使得这7个整数沿圆周排成一圈后，任3个相邻数的和都等于29？如果能，请举一例；如果不能，请简述理由．分析 假设存在7个整数1a ，2a ，3a ，4a ，5a ，6a ，7a 排成一圈后，满足题意，由此展开计算推理．若推得矛盾，则原假设不成立．a4a解 由题意得 12329a a a ++= 23429a a a ++= ……67129a a a ++= 71229a a a ++=将上述7式相加，得()12345673297a a a a a a a ++++++=⨯，12345672673a a a a a a a ∴++++++=，与1234567a a a a a a a ++++++为整数矛盾，故不存在满足题设要求的7个整数． 难解的结英国剑桥大学有一位数学家（真名叫道奇逊），用刘易士·卡洛尔的笔名写了不少非常有趣的科普读物，其中有一本《乱纷纷的结》，书中的每一章都叫做“绳结”，意即这些问题像绳结一样复杂难解，下面就是一个“绳结”的题目：例6 两个步行者正在急促地以每小时6千米的速度向山下走去，一个年轻人像羚羊似的边跳边走，他的同伴吃力地跟在后面．年轻人说，只怪我们上山的时候走得太慢了，每小时只走3千米．在平地的时候走得多快？他的同伴回答，在平路上每小时走4千米．年轻人说，能赶得上回去吃夜饭吗？同伴说，这要看我们了，我们3点钟出来，8点钟该我们回到旅馆的时候了．今天可真走了不少路．年轻人说，到底走了多少路呢？同伴不耐烦地说，你自己去想吧， 题目就是这样，似乎条件不充分，你能解开这个“结”吗？解 设旅行者一共走过的路程为x 千米，上坡（或下坡）走过的路程为y 千米． 整个行程分为四段：走平路、上坡、下坡、再走平路．开始走平路所花的时间是124x y-小时，上坡所花的时间是3y 小时，下坡所花的时间是6y 小时，再走平路所花的时间是124x y-小时．依题意可得方程：112254364x y x yy y --+++=， 原方程化简得154x =，20x =，故他们一共走了20千米． 练一练1．已知2356x y z -=+，6914y z x =--，则x ，y ，z 的平均数是_______________．2．A 、B 两校男生、女生人数的比分别为8:7，30:31，两校合并后男生、女生人数的比是27:26．若用一位整数的比近似表示合并前A 、B 两校的人数的比，则这个近似比是_________．3．甲、乙两车从A 向B 行驶，甲比乙晚出发6小时，开始时甲、乙的速度比是4:3．甲出发6小时后，速度提高1倍，甲、乙两车同时到达B ．则甲从A 到B 共走了_________小时．4．某服装厂生产某种定型冬装，9月份销售每件冬装的利润是出厂价的25%（每件冬装的利润=出厂价-成本），10月份将每件冬装的出厂价调低10%（每件冬装的成本不变），销售件数比9月份增加80%，那么该厂10月份销售这种冬装的利润总额比9月份的利润总额增长（ ）． A ．2% B ．8% C ．40.5% D ．62%5．甲、乙、丙、丁四人，每三个人的平均年龄加上余下一人的年龄分别为29，23，21和17，则这四人中最大年龄与最小年龄的差是（ ）．A ．28B ．27C ．19D ．186．一辆汽车从A 地匀速驶往B 地，如果汽车行驶的速度增加%a ，则所用的时间减少6%，则a 、b 的关系是（ ）．A ．1001%a b a =+B ．1001%b a =+C ．1a b a =+D ．100100ab a=+7．如图33⨯数表各行、各列及两条对角线之和彼此相等，设为S ．求证：ihgf e d c b a（1）3S e =；（2）()24a c g i b d f h e +++=++++．8．在一次数学竞赛中，组委会决定用NS 公司赞助的款购买一批奖品．若以1台NS 计算器和3本《数学竞赛讲座》书为一份奖品，则可买100份奖品；若以1台NS 计算器和5本《数学竞赛讲座》书为一份奖品，则可买80份奖品．问这笔钱全部用来购买计算器或《数学竞赛讲座》书，可各买多少？ 9．甲、乙二人分别从A 、B 两地出发，相向而行．若同时出发，经24分钟相遇；若乙比甲提前10分钟出发，甲出发20分钟与乙相遇，求甲从A 地到B 地、乙从B 地到A 地各需多少分钟？10．在车站开始检票时，有()0a a >名旅客在候车室排队等候检票进站，检票开始后，仍有旅客继续前来排队等候检票进站，设旅客按固定的速度增加，检票口检票的速度也是固定的，若开放一个检票口，则需30分钟才可将排队等候检票的旅客全部检票完毕；若开放两个检票口，则只需10分钟便可将排队等候检票的旅客全部检票完毕；现在要求在6分钟内将排队等候检票的旅客全部检票完毕，以使后来到站的旅客能随到随检，问需要同时开放几个检票口？ 微探究借助图形思考数学是研究数量关系与空间形式的科学，数与形，以及数和形的关联与转化，这是数学研究的永恒主题．当代美国数学家斯蒂恩说：“如果一个特定的问题可以被转化为一个图形，那么思维就整体地把握了问题，并能创造性地思考问题．”现阶段借助图形思考主要体现为：通过构造图形或拼图解与数量关系相关联的问题．例1 A 、B 、C 、D 、E 、F 六个足球队进行单循环比赛，当比赛到某一天时，统计出A 、B 、C 、D 、E 五队已分别比赛了5、4、3、2、1场球，则还没有与B 队比赛的球队是___________． 试一试 用算术或代数方法解，易陷入困境，用6个点表示A 、B 、C 、D 、E 、F 这6个足球队，若两队已经赛过一场，就在相应的两个点间连一条线，这样用图来辅助解题，形象而直观．例2 古希腊人常用小石子在沙滩上摆成各种形状来研究数．比如：他们研究过图①中的1，3，6，10，…，由于这些数能够表示成三角形，故将其称为三角形数，类似地，称图②中的1，4，9，16，…，这样的数为正方形数，下列数中，既是三角形数，又是正方形数的是（ ）． A ．289 B ．1024 C ．1225 D ．1378图①10631图②16941试一试 分析三角形数、正方形数的特征，并用n 的代数式表示． 例3 有足够长的长方形和正方形卡片，如下图：（1）如果选取的1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙），请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．333221这个长方形的代数意义是________________________________________________________（2）小明想用类似方法解释多项式乘法()()2223327a ab a b b a b =++++，那么需要用2号卡片______张，3号卡片___________张．试一试 为避免拼图的盲目性，从整式的乘法入手． 眼见亦可为虚例4 一只小渔船在海上遇到了台风，触到礁石上，船身撞出了一个窟窿．如果不把它堵上，渔船就有沉没的危险．船中只有一块边长是8cm 的正方形木板，但是和船的窟窿相比，木板的面积少21cm ．怎么办好呢？正在焦急当中，有一个船员用锯把这块正方形的木板裁开（如下图），然后用胶粘接拼成了长方形木板．8×8=64cm 2()①②③④535313×5=65cm 2()②①④③3855从图中的计算可知：原来的正方形木板的面积是264cm ，可是改成长方形以后木板的面积却变成265cm 了，正好多出21cm ．船员赶紧把它堵在窟窿上，避免了渔船的沉没．可是大家都感到惊奇的是，这21cm 是从哪里多出来的呢，你能告诉他们吗？ 试一试 略横看成岭侧成峰例5 ()()()()()()22124222a b a b a b a b a b a b a b +-⎡⎤-=+-=+-⨯=⨯⨯⎢⎥⎣⎦． 下面的图形，形象直观验证了平方差公式：aabbb baa柳卡趣题例6 法国数学家柳卡·施斗姆生于瑞士，因数学上的成就，于1836年当选为法国科学院院士，他对射影几何与微分几何研究都作出了重要贡献，在某次国际科学会议期间，一次有许多著名数学家参加的晚宴上，他提出了如下的一个轮船问题，人们称它为“柳卡趣题”．每天中午有一艘轮船从法国巴黎的勒阿佛尔开往美国的纽约，且每天同一时间也有一艘轮船从纽约开往勒阿佛尔，轮船在途中需要七天七夜，假定所有轮船都以同一航线、同速匀速行驶，问某艘从勒阿佛尔开出的轮船，在到达纽约时，能遇到几艘从纽约开来的轮船？这个问题难倒了在场的所有数学家，连柳卡本人也没有彻底解决．后来有一位数学家通过构图解法，才使问题最终得以解决． 解 用“时间—路程图”解答．日期日期纽约勒阿佛尔65432178910111213141516171716151413121110987123456从图上可以很清楚地看到，某艘从勒阿佛尔开出的轮船，在中途可以遇到13艘从纽约开来的轮船，加上开航时与到达时相遇的2艘，因此一共遇到了15艘从纽约开出的轮船． 练一练1．如图，甲类纸片是边长为2的正方形，乙类纸片是边长为1的正方形，丙类纸片是长、宽分别为2和1的长方形，现有甲类纸片1张，乙类纸片4张，则应至少取丙类纸片_______张，才能用它们拼成一个新的正方形．甲乙丙2．有若干张如图①所示的正方形和长方形卡片，如果要拼一个长为()2a b +，宽为()a b +的矩形，则需要A 类卡片___________张，B 类卡片_________张，C 类卡片________张，请你在图②中的大矩形中画出一种拼法．图①C B A abb b aa图②2a +b a +b3．小明在拼图时，发现8个一样大小的长方形如图①所示，恰好可以拼成一个大的长方形． 小红看见了，说：“我来试一试，”结果七拼八凑，拼成如图②那样的正方形． 咳，怎么中间还留下了一个边长为2mm 的正方形洞！ 你能帮他们解开其中的奥秘吗？图①图②4．如图①，现有a a ⨯、b b ⨯的正方形纸片和a b ⨯的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）在下面的虚线方框中拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图痕迹），使拼出的矩形面积为22252a ab b ++，并标出此矩形的长和宽．a ab abb5．用新方法解释旧模式常会推导绝妙的公式．请你依下列图形直观分别写出相应公式．图①2222图④=++36．如图，九块大小不等的正方形纸片A ，B ，…，I 无重叠、无缝隙地铺满了一块长方形，已知E 的边长为7，求其余各正方形的边长．IH GF ED CB A阿28．实验与操作问题解决例1 4-；4- 输入18，依次得到的结果为：9，4，2，1，4-，2-，1-，6-，3-，8-，4-，2-，1-，…显然，除去前4次的结果外，从第5次的结果4-开始，每6次一个循环，而()20094620056334-÷=÷=余1，故第2009次计算的结果为4-． 例2 D例3 （1）当3n =时，13m =；4n =时，17m =；……一般的41m n =+．（2）由41m n =+，得10341n =+，25.5n =，因n 不是正整数，故按此要求操作不可能得到103个正方形．例4 用1997枚硬币的朝向情况可用1997个数的乘积来表示．若这些数之积为1-（或1+），表明有奇数（或偶数枚硬币朝下）．开始时，其乘积为()()1000997111+⨯-=-．每次翻折6枚硬币，即每次改变6个数的符号，其结果是1997个数之积仍为1-．经过有限次翻转后，这个结果总保持不变，即国徽朝下的硬币数永远是奇数枚，故回答是否定的． 数学冲浪1．12.5 画图略 2．5 3．36 4．8 5．略6．或7．先将三个空啤酒瓶放置成底面中心成“正三角形”的位置，再将一个空啤酒瓶倒置放在这个三角形中心P 的位置，保持中心P 的位置不变，适当移动三个底朝下的空啤酒瓶，放大或缩小“正三角形”，可使瓶底中心构成四个边长相等的“正三角形”如图（答案不唯一）．8．9．一个依次排列的n 个数组成一个数串：1a ，2a ，3a ，…，n a ，依题设操作方法可得新增的数为：21a a -，32a a -，43a a -，…，1n n a a --，则新增数之和为：()()()()21324311n n n a a a a a a a a a a --+-+-++-=- （※）原数串为3个数：3，9，8．第1次操作后所得数串为：3，6，9，1-，8，根据（※）可知，新增2项之和为：()61583+-==-，第2次操作后所得数串为：3，3，6，3，9，10-，1-，9，8，根据（※）可知，新增4项之和为()33109583++-+==-，按这个规律下去，第100次操作后所得新数串所有数的和为：()()39810083520+++⨯-=．10．（1）经过6次操作可达到要求：()()()()()()()19,8,921,7,823,6,725,5,624,4,823,3,1022,2,12⇒⇒⇒⇒⇒⇒． （2）不可能．因为每次操作后，每堆码数要么加2，要么少1，而19，8，9被3除余数分别为1，2，0，经过任何一次操作后余数分别是0，1，2，不可能同时被3整除．11．不可能 我们设想36个展室都依次相间地铺上了两种颜色的地毯，则参观者无论怎样走法，只能按白→黑→白→黑→白→……的次序前进．因此，不管参观者怎样走法，第36次只能走到一间黑色地毯的展室，绝不可能走到铺白色地毯的展室出口．出口12．（1）把可分得的边长为整数的长方形按面积从小到大排列，有11⨯，12⨯，13⨯，14⨯，22⨯，15⨯，23⨯，24⨯，33⨯，25⨯，34⨯，35⨯．若能分成5张满足条件的纸片，因为其面积之和应为15，所以满足条件的有11⨯、12⨯、13⨯、14⨯、15⨯（如图①）或11⨯、12⨯、13⨯、22⨯、15⨯（如图②）图①图②（2）若能分成6张满足条件的纸片，则其面积之和仍应为15，但上面排在前列的6个长方形的面积之和为1112131422151915⨯+⨯+⨯+⨯+⨯+⨯=>．所以分成6张满足条件的纸片是不可能的． 13．（1）略；（2）1S 、2S 、3S 的结果都是ab b -；（3）这是有关道路形状及草地面积的研究题，其中包含阅读、作图、计算及猜想等步骤．关键是探索：当道路由笔直到任意弯曲的变化中，矩形中空白部分（即草地）面积情况．猜想：依据前面的计算，无论小路怎么弯曲，可以猜想草地的面积仍然是ab b -．方法是将“小路”沿左右两个边界剪去，将其中一侧的草地平移一个单位向另一侧草地靠拢，得到一个新的矩形． 此时，在新的矩形中，其纵向宽仍然是b ，其水平方向的长度变成了1a -，所以草地面积是()1b a ab b -=-．设而不求（微探究） 例1 乙 所得差()()1190990e a d b =⨯-+-⎡⎤⎣⎦是11的倍数例2 B 设水果质量为m ，进价为a ，售价在进价的基础上至少提高x ，则()101120100100m x a ma ma⎛⎫-+- ⎪⎝⎭=，解得33.4%x ≈． 例3 设白天的单价为a 元/度，晚间的单价比白天低的百分数为x ，即晚间的单价为()1x a -元/度，又设8月份晚间用电量为n 度，则8月份白天用电量为()150% 1.5n n =+度，8月份电费为。

第五届全国中学生数理化学科能力展示活动 七年级数学解题技能展示试题及解答 试卷说明：1、本试卷共计15题，满分为120分 2、考试时间为120分钟 一、选择题（共6小题，每题6分，共36分） 1、在“桑迪”飓风中，一家美国商店的某种商品被歹徒偷走了1/5,被水损坏了1/6.剩下的全部售出，结果这种商品还盈利14%。

那么这种商品的售价与进价之比为 . A. 9：5 B. 2:1 C. 3:2 D. 5:3解：设进价为a ,售价为b,则 a(1+14%)=b(1-1/5-1/6), 114%·a=19/30·b, b:a=9:5. 2、一种叫“快乐”的微生物由快乐细胞组成。

1个快乐细胞每次裂变为5个快乐细胞，这5个快乐细胞中的每一个又可依次裂变为5个快乐细胞，依次类推。

那么在一定时间内，1个快乐细胞可以裂变为（ ）个快乐细胞。

A. 2012 B. 2013 C. 2014 D. 2015解： 因为， 625=54 < (2012-2015) < 55 =3075 所以625个快乐细胞未完全裂变，设其中有x 个已裂变，则裂变总数为 （625-x ）+5x=625+4x=4（156+x ）+1 符合条件的只有（B ） 3、机器猫跑7步与机器狗跑5步的路程相同；机器狗跑11步与机器人跑7步路程相同。

机器猫跑5步的时间与机器狗跑3步的时间；机器狗跑7步的时间与机器人跑5步的时间相同。

那么机器猫、机器人的速度之比为（ ） A. 33:35 B. 25:21 C. 35:33 D. 49:55 解：设机器猫每步跑a 米，速度为x 米/秒；设机器狗每步跑b 米，速度为y 米/秒；设机器人每步跑c 米，速度为z 米/秒. 7a=5b,11b=7c; a:c=5:11. 又:5a/x=3b/y,7b/y=5c/z;从而5a/3x=b/y=5c/7z;x:y=7a/3c=7/3·5/11 =35:33 4、1233+78被111除的商和余数分别是（ ）。

七年级综合知识竞赛数 学 试 卷一．选择题（每小题3分,共30分）1。

下列各方程中，是二元一次方程的是（ ） A ．y x yx +=-523 B ．3x +1=2xy C ．51x =y 2+1 D ．x +y =12．下列运算正确的是( ）A ．()333a b a b +=+ B ．326236a a a ⋅=C ．()4312xx -= D ．()()32n nn x x x -÷-=-3。

如图，直线a ∥b ，∠1=70°，那么∠2的度数是（ )A ．130°B 。

110°C 。

70° D. 80° 4. 下列分解因式正确的是（ ）A ．()()422xy x y -=-+B ．()36332x y x y -+=-C ．()()2221x x x x --=+-D ．()22211x x x -+-=--5． 如(x +m ）与（x +3）的乘积中不含x 的一次项，则m 的值为（ ） A 、–3 B 、3 C 、0D 、16．要使分式)2)(1(2-+-x x x 有意义,x 的取值应该满足（ )A 。

1-≠xB . 2≠xC . 1-≠x 或 2≠xD .1-≠x 且 2≠x7．已知{21x y ==是二元一次方程组{81mxny nx my +=-=的解，则2m －n 的算术平方根为（ ) A 。

2± B 。

2 C 。

4 D 。

2 8．若x,y 均为整数，且124128x y +⋅=,则x y +的值为（ ）A ．4B ．5C ．4或5D ．无法确定 9．（－2）2015 +(－2）2016所得的结果等于（ ）A ．22015B ． －22015C ． －2 2016D ．210。

如图，在平面内，两条直线l 1，l 2相交于点O ，对于平面内任意一点M ，若p ，q 分别是点M 到直线l 1，l 2的距离，则称(p ,q ）为点M 的“距离坐标”．根据上述规定，“距离坐标”是（2，1)的点共有（ ）个．ab21（第3题图）A ．8B ．4C ．2D ．1二．填空题（每小题3分，共24分．) 11．分解因式：2161a -＝ ．12．某种感冒病毒的直径是0. 00000012米，用科学记数法表示为 米．13.若m 为正实数,且13m m-=，221m m +=__________________________ 。

第九届全国中学生数理化学科能力展示活动七年级数学解题技能展示试题(A卷)赛区㊀学校㊀㊀姓名㊀准考证号考生须知:１．请将答题纸工整撕下并在答题纸和试卷上填写有效信息;２．考生必须在答题纸上答卷,否则成绩无效;３．考试时间为１２０分钟,满分１２０分．４．成绩查询:２０１７年１月５日起,考生可通过活动官方网站 理科学科能力评价网 (w w w．x k s l h．c o m)查询自己的分数及获奖情况．一㊁选择题(每题６分,共４８分,每题只有１个选项是正确的)１． 钋 是世界上最毒的物质,０ １g钋可以杀死１０００亿人,钋Ｇ２１０最大摄入量为万亿分之０ ８g．用科学计数法表示钋Ｇ２１０的最大摄入量为(㊀㊀)．A㊀０．８ˑ１０－１２g;㊀㊀B㊀８ˑ１０－１３g;㊀㊀C㊀０．８ˑ１０１２g;㊀㊀D㊀８ˑ１０１３g２．计算２０１６２０１６２２０１６２０１５２＋２０１６２０１７２－２的值为(㊀㊀)．A㊀１２;㊀㊀B㊀１;㊀㊀C㊀２;㊀㊀D㊀３２３．若把能表示为两个连续偶数的平方差的正整数称为 和平数 ,则在１~１００这１００个数中,能称为 和平数 的所有数的和是(㊀㊀)．A㊀１３０;㊀㊀B㊀３２５;㊀㊀C㊀６７６;㊀㊀D㊀１３００４．T h e s t u d e n t s i n M r s．S a w y e r sc l a s sw e r ea s k e dt od oat a s t et e s t o f f i v ek i n d s o f c a n d y．E a c hs t u d e n t c h o s e o n ek i n do f c a n d y．Ab a r g r a p ho f t h e i r p r e f e r e n c e s i ss h o w n．W h a t p e r c e n to fh e rc l a s s c h o s e c a nd y E(㊀㊀)?５．无限循环小数为有理数,如:０．１ ,０．２ ,０．３ , ,观察０．１ ＝１９,０．２ ＝２９,０．３ ＝１３, ,则可归纳出０．４ ５ ＝(㊀㊀)．A㊀１２;㊀㊀B㊀５１１;㊀㊀C㊀１２０;㊀㊀D㊀５１１０６．如图的矩形A B C D中,点E在C D上,且A E＜A C．若P㊁Q两点分别在A D㊁A E上,A PʒP D＝４ʒ１,A QʒQ E＝４ʒ１,直线P Q交A C于点R,且Q㊁R两点到C D的距离分别为q㊁r,则下列关系中正确的是(㊀㊀)．A㊀q＜r,Q E＝R C;㊀㊀㊀B㊀q＜r,Q E＜R C;C㊀q＝r,Q E＝R C;㊀㊀D㊀q＝r,Q E＜R C７．如图甲,O P为一条拉直的细线,A㊁B两点在O P上,且O AʒA P＝１ʒ３,O BʒB P＝３ʒ５．若先固定点B,将O B折向B P,使得O B重叠在B P上,如图乙．再从图乙中的点A及与A重叠处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为(㊀㊀)．A㊀１ʒ１ʒ１;㊀㊀B㊀１ʒ１ʒ２;㊀㊀C㊀１ʒ２ʒ２;㊀㊀D㊀１ʒ２ʒ５８．在湖南卫视 我是歌手 节目中,有五位歌手角逐前５名．在公布成绩时,导演对其中一位歌手A说:你没得第一名;又对另一位歌手B说:你是第三名．请你分析一下,这五位歌手的名次不同排列的种数为(㊀㊀)．A㊀２４;㊀㊀B㊀２０;㊀㊀C㊀１８;㊀㊀D㊀６二、填空题(每题８分,共３２分)９．我国明代珠算家程大位的名著«算法统宗»里有一道著名算题: 一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁 ?这道题的答案是．１０．某场音乐会观众的座位分成一楼与二楼两个区域．若一楼售出与未售出的座位数比为４ʒ３,二楼售出与未售出的座位数比为３ʒ２,且此场音乐会一㊁二楼未售出的座位数相等,则此场音乐会售出与未售出的座位数比为．１１．小昱和阿帆均从同一本书的第１页开始,逐页依顺序在每一页上写一个数．小昱在第１页写１,且之后每一页写的数均为他在前一页写的数加２;阿帆在第１页写１,且之后每一页写的数均为他在前一页写的数加７．若小昱在某页写的数为１０１,则阿帆在该页写的数为．１２．对大于１的自然数m 的三次幂可用奇数进行以下方式的 分裂 :２３３,５,{３３７,９,１１,ìîíïïïï４３１３,１５,１７,１９,ìîíïïïïïï 仿此,若m ３的 分裂 数中有一个是２０１７,则m 的值为．三、解答题(本题共３小题,共４０分)１３．(１３分)流程图是为了清晰描述某事件或规律而用特殊形状㊁符号及相应规则绘制出的框图结构．给出一个如图所示流程图,其作用是输入x ,输出相应的y 值．若要使输入的x值与输出的y 值相等,则输入的x 值有多少个?分别是什么?１４．(１３分)在平面上的一个直角三角形中,两个直角边的平方加起来等于斜边的平方．如果设直角三角形的两条直角边长分别是a 和b ,斜边长是c ,则有a ２＋b ２＝c ２．这就是著名的勾股定理．如图,在直角әA B C 中,øA C B ＝９０ʎ,C D ʅA B 于点D ,D E ʅA C 于点E ,D F ʅB C 于点F ．求证:A E B F A B ＝C D ３．１５．(１４分)梓才中学有３３３人参加了 全国中学生数理化学科能力展示活动七年级数学解题技能展示 考试,电脑阅卷系统显示这３３３人一共做对了１０００道选择题．组委会规定做对３道及以下为不合格,做对６道及以上为优秀,其中不是所有人做对题目数量的奇㊁偶性都相同,问不及格及优秀的人数哪个多?。

第五届全国中学生数理化学科能力展示活动八年级数学解题技能展示试题解答试卷说明：1、本试卷共计15题，满分为120分2、考试时间为120分钟 一、选择题（共6小题，每题6分，共36分）1、已知a=2010x+2011,b=2010x+2012,c=2010x+2013,则多项式a 2＋b 2＋c 2－ab －bc －ca 的值为D .A. 0； B. 1； C. 2； D. 3解：a 2＋b 2＋c 2－ab －bc －ca=21[（a-b ）2＋(b-c)2＋(c-a)2] =21×6=3 2、直角三角形ABC 中，∠ABC=90°，AB=CB ，D 为AB 延长线上一点，点E在边BC 上，且BE=BD ，则∠BCD 与∠CAE 的度数和为B 资料个人收集整理，勿做商A. 30°B. 45°C. 60°D. 75°解： 因为， △ABE ≌△CBD ，所以∠BCD=∠BAE .∠BCD+∠CAE=∠BAE+∠CAE=∠BAC=45°.3、In the United States,have the followingthicknesses:penny,1.55mm;nickel,1.95mm;dime,1.35mm;quarter,1.75mm.If a stack of these coins is exactly 14 mm higt,howmany coins are in the stack?（B ）A. 7; B. 8; C.9; D. 10. 解：译文：在美国,有以下厚度的硬币：1美分，1.55mm;5美分,1.95mm;1角硬币1.35m;四分之一美元,1.75mm.如果一堆这些硬币正是14毫米,有多少硬币堆在一起?资料个人收集整理，勿做商业用途设4种硬币的数量分别为a 、b 、c 、d.则1.55a+1.95b+1.35c+1.75d=14,155a+195b+135c+175d=1400,31a+39b+27c+35d=280,3a+11b －c+7d+28(a+b+c+d )=280,3a+11b －c+7d=28[10－(a+b+c+d)]∴a+b+c+d ≦10.当a+b+c+d=10（1）时，3a+11b －c+7d=0（2）（1）+（2）得：4a+12b+8d=10,2a+6b+4d=5(左偶右奇，不合题意)同理当a+b+c+d=9时，4a+12b+8d=37(左偶右奇，不合题意)当a+b+c+d=7时，4a+12b+8d=7+3×28(左偶右奇，不合题意)只有a+b+c+d=8符合。

七 年 级 数 学 试 题（沉着冷静，细心答题；挑战自我，相信自己！）题号题号 一 二 三总分总分 13 14 15 16 17 得分得分一、精心选一选，相信你选得准！（每小题（每小题55分，共分，共303030分）分）分）1．已知201020102010201120112011+´-´-=a ，201120112011201220122012+´-´-=b ，201220122012201320132013+´-´-=c ，则abc的值为（的值为（ ）． A ．－3 B ．－1 C ．3 D ．1 2．如图，已知B 、C 是线段AD 上任意两点，M 是AB 的中点，N 是CD 的中点，若MN ＝a ，BC ＝b ，则AD 的长等于（的长等于（ ）． A ．2a －b B ．ab －a C ．a ＋2b D ．2a ＋b 3．如果a 、b 、c 为非零的有理数，且a ＋b ＋c ＝0，则||||||||abc abcc c b b a a -++的所有可能的值为（值为（ ）． A ．0 B ．1或－1 C ．0或－2 D ．2或－2 4．如图AB ∥EF ，设∠C ＝90o ，∠B 、∠D 、∠E 三个角的大小分别为x 、y 、z ，则x 、y 、z 之间满足的关系式是（之间满足的关系式是（ ）。

A ．y ＝x ＋zB ．x ＋y ＋z ＝180oC ．x ＋y －z ＝90oD ．y ＋z －x ＝90o5．已知x 、y 、z 、a 、b 均为非零的实数，且满足331b a y x xy -=+，31a z y yz =+，331b a z x xz +=+，121=++zx yz xy xyz ，由a 的值为（的值为（ ）． A ．2 B ．－2 C ．1 D ．－1 6．设a 、b 、c 平均数为M ，a 、b 平均数为N ，N 与c 平均数为p ，如a ＞b ＞c ，则M 与p 的大小关系是（的大小关系是（ ）． A ．M ＝pB ．M ＞pC ．M ＜pD ．不能确定．不能确定ABCDEFxyzA D M BC N二、填空题（每题5分，共30分）7．8)34(,343-=+=-y x y x ，则3y x +＝_____________．8．若方程组ïîïíì=+=+=+468x z z y y kx 的解使得kx ＋2y －z 的值为10，则k ＝_______________．9．如图在长方形ABCD 中，E 是AD 的中点，F 是CE 的中的中点，若△BDF 的面积为2cm 2，则长方形ABCD 的面积为的面积为__________cm 2．10．如图，图中有线段a 条，小于180o 的角有b 个，则a ＋b ＝_________． 11．长90米的列车的速度是54千米/小时，它追上并超过60米的列车用了15秒；如果这两列火车相向而行，从相遇到完全离开需用__________秒．秒． 三、解答题三、解答题((共40分）13．(6分）某公司只生产普通汽车和新能源汽车，该公司在去年的汽车产量中，新能源汽车占总产量的10%，今年由于国家能源政策的导向和油价上涨因素的影响，计划将普通车的产量减少10%，为保持总产量与去年相等，那么今年新能源汽车的产量应增加的百分数为多少？的百分数为多少？AB 1B 2 B 3B 4 B 5 B 6 B 7ABCDE F14．（8分）某服装厂生产一种西服和领带，西服每套定价为200元，领带每条定价为40元，厂方开展促销活动期间，向客户提供两种优惠方法：①买一套西服送一条领带；套．②西服和领带均按定价的九折付款，某商店到该服装厂买西服20套．条时，通过计算说明应采用哪一种方案购买更优惠．⑴若购买的领带为50条时，通过计算说明应采用哪一种方案购买更优惠．⑵领带买多少条时，两种优惠方法付款一样多．⑵领带买多少条时，两种优惠方法付款一样多．16．（10分）将连续自然数1—1015按如图方式排列成一个长方形阵列，用一个正方形框出16个数。

第九届全国中学生数理化学科能力展示活动七年级数学解题技能展示试题（A 卷）答案一、选择题（每题6分，共48分）1.B ．2.A.解析设20162016=x ，则原式为212)1()1(222=-++-x x x ．3.C ．解析设两个连续偶数为2k ＋2和2k (k 为正整数)，则(2k ＋2)2－(2k )2＝4(2k ＋1)，故和平数是4的倍数，但不是8的倍数，故在1～100之间，能称为和平数的有4×1,4×3,4×5,4×7,…,4×25，共计13个，其和为4×1＋252×13＝676.4.D ．解析（译）索耶太太班上的学生被要求给五种糖果做味觉测试，每个学生选择一种糖果。

条形图显示其偏好。

全班学生中有百分之多少选择糖果E ？答案：5/25=20%.5.B .解析观察知0.1·＝19，0.2·＝29，0.3·＝39，…，所以可归纳出0.4·5·＝4599＝511.6.D.解析∵在矩形ABCD 中，AB ∥CD ，∵AP ：PD=AQ ：QE=4：1，∴QE AQ PD AP =，∴PQ ∥CD ，∴4==QEAQ RC AR ，∵平行线间的距离相等，∴q=r ，∵4==QE AQ RC AR ，∴51==AC CR AE QE ，∵AE ＜AC ，∴QE ＜CR ．7.B.解析设OP 的长度为8a ，∵OA ：AP=1：3，OB ：BP=3：5，∴OA=2a ，AP=6a ，OB=3a ，BP=5a ，据题意剪开后所得三段从小到大的长度分别是：2a 、2a 、4a ，∴此三段细线由小到大的长度比为：2a ：2a ：4a =1：1：2。

8.C ．解析首先排A ，A 可在第2,4,5三个名次上，有3种排法，C ，D ，E 的排列，有6种名次排法，即这五位学生的名次排列种数为3×6＝18种．二、填空题（第题8分，共32分）9.大和尚25人；小和尚75人。

全国中学生数理化学科能力竞赛简介全国中学生数理化学科能力竞赛是面向全国中学生的一项富有挑战性和指导性的学科竞赛活动。

该竞赛旨在通过比赛形式，提高中学生的数理化学学科素养和综合应用能力，激发学生对数理化学科的兴趣和热爱，培养科学精神和创新意识。

竞赛内容全国中学生数理化学科能力竞赛主要涵盖数学、物理和化学三个学科的内容。

竞赛题目旨在考察学生对基础知识的理解和掌握程度，以及解决实际问题的能力和创新思维。

题型一般为选择题、填空题和解答题，难度逐渐递增，旨在对学生的数理化综合能力进行全面考核。

竞赛组织全国中学生数理化学科能力竞赛由教育行政部门主办，各地区教育部门和学校共同组织。

竞赛分为初赛和决赛两个阶段。

初赛由各地区学校自行组织，决赛则由教育行政部门统一安排。

初赛采取校内选拔形式，决赛则是在特定场地进行的综合性考试。

竞赛意义全国中学生数理化学科能力竞赛对于中学生的成长和发展具有重要意义。

首先，通过竞赛的形式，可以激发学生学习数理化学科的兴趣和热爱，培养科学精神和创新意识。

其次，竞赛能够全面考核学生的数理化综合能力，提高学生解决实际问题的能力和创新思维。

此外，竞赛还能够促进学生相互之间的交流和竞争，激发学生的学习动力，推动学生的个人发展。

竞赛影响全国中学生数理化学科能力竞赛在教育领域具有广泛的影响。

一方面，竞赛有助于提高中学生的数理化学学科素养，培养创新精神和实践能力，为高等教育的发展提供源源不断的人才支持。

另一方面，竞赛活动也为学校和教育部门提供了一个对教育教学质量进行评估和提升的平台，有助于推动教育教学改革。

总结全国中学生数理化学科能力竞赛是一项有益于中学生综合能力发展的活动。

通过参加竞赛，学生可以提高数理化学科的学习兴趣和热爱，培养科学精神和创新意识。

同时，竞赛也为学校和教育部门提供了一个评估和提升教育质量的平台。

全国中学生数理化学科能力竞赛的影响正逐渐扩大，对于推动中学生素质教育的发展起到积极的促进作用。