缓和曲线放样(ZLL)
- 格式:doc
- 大小:864.06 KB
- 文档页数:12



收稿日期:2005-08-04作者简介:王新民, 男, 济南城建工程公司工程师。
带有缓和曲线的圆曲线放样新方法王新民1, 张祥龙2(1、济南城建工程公司, 山东济南250031; 2、山东广播电视大学, 山东济南250014摘要:传统的曲线放样方法由于经常受施工现场地形、交通等条件的限制而无法进行, 而利用全站仪按坐标放样的方法可灵活解决以上难题。
本文以切线支距法测设曲线的计算公式为基础, 通过坐标转换, 导出了曲线上任一点在城市统一坐标系坐标的计算公式, 并结合工程实践总结了利用全站仪放样曲线的优越性。
关键词:缓和曲线; 圆曲线; 坐标法; 坐标转换; 曲线放样中图分类号:TU 198文献标识码:A 文章编号:1008-3340(2006 01-0071-02道路曲线放样的传统方法主要有偏角法、切线支距法、弦线偏距法等, 这些方法通常是将仪器架设在曲线的起点、终点或其它要素点进行测设, 适用于地势平坦地区, 通视条件好且易于量距, 但遇到丘陵地区或者线路跨沟过河等情况就行不通。
随着全站仪在工程测量中的普及应用, 一种新的曲线放样方法──坐标法[2]在工程实践中得到了广泛的应用。
这种方法是先计算出曲线上任意点的城市统一坐标系坐标, 然后利用导线点用极坐标法现场放样[3]。
1曲线坐标计算 1. 1坐标系的建立首先假定一个独立曲线坐标系。
如图1所示, 建立以ZH 点为坐标原点, 过该点切线为x 轴, 法线方向为y 轴的曲线坐标系。
1. 2曲线起终点坐标计算设计部门一般给出曲线交点(J D 的城市坐标及其方位角θ, 曲线起点(ZH 、终点(HZ 坐标若未给出, 则可由JD 根据设计曲线参数(T h 、α 很容易推算出来。
1. 3缓和曲线上任意一点坐标计算缓和曲线上任意一点N 的曲线坐标系坐标(x n , y n 的计算公式[1]:x n =l n -l 5S 40R 2l 2S y n l 36R l S(1式中:l n -曲线上任一点N 到ZH 点的曲线长度(里程差;l s -缓和曲线长度;R -缓和曲线终点的圆曲线半径。

道路施工中缓和曲线的放样方法浅析1 概述在道路施工定线时,由于受地形因素的影响,线路在平面上不可避免地要变更方向。
因此,定向测量所决定的线路一般都是由折线组成。
为了满足行车方面的要求,在相邻两直线段之间就必须采用曲线加以连接。
在公路线路上,当二级线路的半径在平原微丘区大于2500米,在山岭重丘区大于600米,三级线路的半径在平原微丘区大于1500米,在山岭重丘区大于350米时可以采用圆曲线。
除上述情况外,均应在直线和圆曲线之间插入缓和曲线。
由以上可知,缓和曲线和圆曲线在公路施工中是非常重要也是经常会遇到的。
当施工中遇到这两种曲线时,采用那种放样方法能够更快更准的进行放样呢?目前大多数参考书及工具书上介绍的还是以前用经纬仪架站,采用偏角法或直角坐标法等传统的方法,工作量大而且计算繁琐,精度不高,容易出错。
在全站仪和计算器越来越普及的情况下,如何找到一种更简单快捷准确的放样方法,将测量人员从繁重的工作中解放出来,成了广大测量人员的心愿。
2 缓和曲线特点车辆在曲线上行驶时会产生离心力,使车身沿半径方向向外推。
离心力的大小与车辆的质量以及车辆在曲线上的运动的速度的平方成正比,与曲线的半径成反比。
为了保持车身的平稳,在铁路上是使外轨对内轨增加高度、在公路曲线上提高外侧路面,即设置超高的方法,使车身向内侧倾斜,由此产生的向内的水平分力与离心力相抵消。
但在由直线进入圆曲线的时,外侧轨道不能突然增加超高。
为了解决这个问题,就要在直线与圆曲线之间设置缓和曲线。
缓和曲线是一种曲率半径按一定规律变化(或从小到大,或从大到小)的曲线。
缓和曲线多数由螺旋线构成,它的特点是曲线上任一点的曲率半径R与该点至起点的曲率长L成正比。
缓和曲线的要素有:T-切线长;L0-缓和曲线长;B0-缓和曲线的倾角;P-缓和曲线的内移值;M-切线的外延量。
3 缓和曲线在道路施工放样中的应用在实际施工中,现场的情况千变万化,我们预先计算的点不一定都能够在现场放上,而且有时有些部位需要加密,在地形变化大的地方需要补点。

一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s=Δa/t≤0.62)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
发布日期:2012-01-31 作者:李秋生浏览次数:1494)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。


浅谈缓和曲线坐标放样计算程序的设计摘要: 缓和曲线是道路平面线形要素之一,在现代高速公路上,缓和曲线所占的比例超过了直线和圆曲线,成为平面线形的主要组成部分。
随着全站仪的广泛使用,在工程测量中利用坐标放样的方法已占据导地位,因此,对缓和曲线的放样,关键就在于计算曲线上点的坐标,关于这方面的内容,现有资料上介绍的一些方法,普遍存在着不直观、不灵活且较繁杂等不足,为此,笔者将在本文中对缓和曲线坐标放样计算程序的设计做一些新探索。
关键词: 缓和曲线加圆曲线放样点坐标计算程序开发一、缓和曲线的概念缓和曲线指的是平面线形中,在直线与圆曲线之间设置的曲率连续变化的曲线。
缓和曲线是道路平面线形要素之一,在现代高速公路上,缓和曲线所占的比例超过了直线和圆曲线,成为平面线形的主要组成部分。
在城市道路上,缓和曲线也被广泛地使用。
如图(1)所示:在直线与圆曲线之间加设一段缓和曲线,其曲率半径ρ从直线的∞(无穷大)逐渐变化到圆曲线的半径R,在缓和曲线上任一点的曲率半径ρ与曲线长度L 成正比,即:ρ∝1/L或ρ.L=C (1)式中C为常数。
当L=Lo时,ρ=R,则有:C=R.Lo (2)式(1)、(2)是缓和曲线必要的前提条件。
在实际应用中,可采取符合这一前提条件的曲线作为缓和曲线。
常用的有辐射螺旋线及三次抛物线,我国采用辐射螺旋线。
二、缓和曲线的数学模型按上述前提条件导出缓和曲线上任一点的坐标x 、y为:三、几个常数的计算在计算缓和曲线放样坐标时,需要用到缓和曲线的几个重要常数,如图(3)。
他们分别是:缓圆点坐标(x0 ,y0)、缓和曲线的切线角β0 、切垂距m、及圆曲线平移量P,现分别计算如下:1、计算缓圆点坐标(x0 ,y0) 由缓和曲线的表达式:2、计算缓和曲线的切线角β0 如图(4):四、曲线上任意一点的坐标公式如图(5)所示:感谢您的阅读,祝您生活愉快。


带缓和曲线放样数据计算①需求:1.缓和曲线常数:缓和曲线切线角β、切垂距m 、内移距p ;2.曲线要素:切线长T 、曲线长L 、外矢距E 、切曲差q ;3.曲线主点里程和坐标:直缓点ZH 、缓圆点HY 、曲中点QZ 、圆缓点YH 、缓直点HZ 。
4.曲线桩点里程和坐标。
②思路:1.已知条件:偏角(转角):α 曲线半径:R 缓和曲线长:0l 交点JD 里程:DK***+***.*** 三个控制点坐标:JD :(xjd ,yjd ) QD :(xqd ,yqd ) ZD :(xzd ,yzd )2.计算公式:1)缓和曲线常数(1)缓和曲线切线角β——Rl R l ⋅=⋅=ππβ00901802 (2)切垂距m ——2302402Rl l m -= (3)内移距p ——R l p 2420=2)曲线要素(1)切线长T :mp R T +⋅+=)2tan()(α(2)曲线长L :02180)2(l R L +⋅-⋅=πβα(3)外矢距E :R p R E -+=)2cos(α(4)切曲差q :L T q -=2 3)计算曲线主要点里程0000)5( 2)4(2)3( )2( )1(l YH HZ l LQZ YH l L HY QZ l ZH HY T JD ZH +=-+=-+=+=-=里程里程里程里程里程里程里程里程里程里程注意:里程直接以米为单位写数值,写成DK***+***.***的形式。
4)切线支距法计算数据根据公式计算,分别求得直缓点ZH 、缓圆点HY 、曲中点QZ 、圆缓点YH 、缓直点HZ 和各桩点的坐标值。
JDQD JD QD ZH i JD QD JD QD ZH i QDJD QD JD JD QD QD JD JD ZH QD JD JD ZH JD QD JD QD QD JD y x Y Y y x X X X X Y Y T Y Y T X X X X Y Y Tl DK ---------+=++=--=⨯+=⨯+=--=+ααααααααcos sin sin cos )arctan(sin cos )arctan(R 已知数据:HY ***.******i i i i 0坐标方位角:坐标方位角:缓圆点第一段:JDQD JD QD ZH i JD QD JD QD ZH i ZH ZH JD QD y x Y Y y x X X Y X ZH p m HY DK HY DK HY ------+=++=++αααααβcos sin sin cos ),( ***.****** ***.****** i i i i 已知数据:圆缓点曲中点第二段:缓圆点ZDJD y x Y Y y x X X T Y Y T X X X X Y Y HZ DK YH ZD JD HZ i ZD JD ZD JD HZ i ZD JD JD HZ ZD JD JD HZ JDZD JDZD ZD JD ---=+-=⨯+=⨯+=--=+------αααααααααcos sin sin cos sin cos )arctan(***.****** i i i i 坐标方位角:缓直点第三段:圆缓点③步骤:1.输入已知参数;2.点击计算。

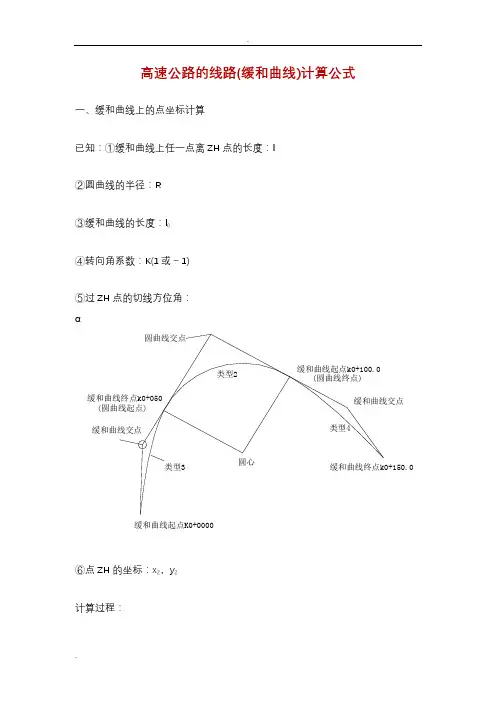
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R 2——曲线终点处的半径P——曲线起点处的曲率1——曲线终点处的曲率P2α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i(上坡为“+”,下坡为“-”)1(上坡为“+”,下坡为“-”)②第二坡度:i2③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K③曲线终点桩号:K1④曲线起点坐标:x0,y⑤曲线起点切线方位角:α⑥曲线起点处曲率:P(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
缓和曲线设计及放样步骤一、 计算部分1、 已知:交点偏角α左=2°06′08.8″=2.1024°(交点桩号)交点7 K5+969.271 α左/2=1.051222设曲线半径R=4000 经计算得:(5)圆曲线 L=180R πα=1804000*1024.2*π=146.778米(4)T=R ×tag2α=73.397米 (6)E=R(sec 2α-1)+0.673米 (7) (D)切曲差2T-L=0.016米根据半径和计算行车速度、公路等级确定l h =60米(1)β=π90*R l h =28.64789R l h =0.4297°=0°25′47″ ∆h =3β=0.14327°=0°08′35.6″ X h =l h -R l h 403=60米Y h =R l h 62-34336R l h =0.15米(2)q= X h -R sin β=2hl -23240R l h =30米(3)p= Y h -R(1-cos β)=Rl h 242=0.0375米 C h = X h - sec ∆h =58.999米T d = X h - Y h ctg β=40米(14)t=p tg 2α+q=30.001米(15)e=p sec 2α=0.0375米 (16)d=2t- l h =0.002米(20)(D h )校正值为:d+切曲差(D)=0.018米(8) (L ′=180πR(α-2β)=86.778米得:(17)T h =T+t=103.398米(18)L h =L+l h = L ′+2 l h =206.778米(19)E h =E+e=0.711米2、桩号计算(9)ZH:K5+969.271- T h =K5+865.873(10)HY:K5+865.873+ l h =5+925.873(11)QZ:K5+865.873+ L h /2=5+925.873+ L ′/2=5+969.262(12)YH:K5+969.262+ L ′/2=6+012.651(13)HZ:K6+012.651+ l h =6+072.651二、 放线部分1、 支经纬仪于JD ,根据T h 、T d 、E h 在两个方向上分别定出ZH 、Q 、QZ(预留闭合用)、Q 、HZ 点。
公路缓和曲线段原理及缓和曲线计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s2)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
βx=s2/2Rl h(2)缓和曲线的总切线角β=l h2)缓和曲线直角坐标任意一点P处取一微分弧段ds,其所对应的中心角为dβxdx=dscosβxdy=dssinβx3)缓和曲线常数(1)主曲线的内移值p及切线增长值q内移值:p=Y h-R(1-cosβh)=l h2/24R切线增长值:q=X h-Rsinβh=l h/2-lh3/240R2(2)缓和曲线的总偏角及总弦长总偏角:βh=l h/2R总弦长:C h=l h-l h3/90R2O为圆曲线的圆心,圆曲线所对圆心角(等于公路偏角)。
第三节 缓和段一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用 1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车 4)与圆曲线配合得当,增加线形美观 2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A 2/ρ(A :与汽车有关的参数)ρ=C/s C=A 2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R ,l h =s 则 l h =A 2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a 1=0,a 2=v 2/ρ,a s =Δa/t ≤0.6 RVl h 3035.0≥2)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s) 2.16.3V t V vt l h ===3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
ph l c h ≥4)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算 1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
目录第一部分:坐标放样竞赛题目第二部分:缓和曲线基本知识点讲解第三部分:根据例题来计算第四部分:自己做练习第一部分:坐标放样竞赛题目工程施工放样竞赛样题已知某道路曲线第一切线上控制点ZD1(500,500)和JD1(750,750),该曲线设计半径R=1000m,缓和曲线长L0=100m,JD1里程为DK1+300,转向角α右=23°03′38″。
请按细则要求使用非程序型函数计算器计算道路曲线主点ZH、HY、QZ点坐标,及第一缓和曲线和圆曲线上中桩点K1+100、K1+280的坐标,共计算5个点。
然后,根据现场已知测站点O、定向点A、定向检核点B,使用全站仪进行第一缓和曲线和圆曲线上中桩点放样K1+100和K1+280点。
控制点和待放样曲线之间关系如图所示。
已知点有两套坐标,第一套坐标供放样,第二套坐标供检测(该套坐标放样完成后需检测时,请选手向裁判索要)。
实施步骤:(1)计算道路曲线常数、曲线要素、主点里程、主点及若干曲线中桩点坐标;(2)在测站点安置全站仪,定向,测量方向检核点的坐标,对定向方向进行检核;(3)根据计算出的中桩点坐标,用全站仪点进行曲线中桩点实地放样,并在地面上做好标记;(4)在放样点上安置棱镜等待裁判实测已放样点位坐标确定点位放样的精度。
曲线常数、要素、主点里程及中桩坐标计算成果表第二部分:缓和曲线基本知识点讲解铁路、公路在线路方向改变时,在转向处需要用曲线将两直线连接起来,常见的曲线形式有圆曲线、缓和曲线等。
圆曲线是具有一定半径的圆弧。
缓和曲线是曲率半径从无穷大逐渐变到圆曲线半径R。
下图为缓和曲线的图示:一、缓和曲线的主点:直缓点ZH、缓圆点HY、曲中点QZ、圆缓点YH、缓直点HZ。
解释:直缓点表示由直线过度到缓和曲线的点。
字母是汉语拼音的首字母。
其他点同理。
二、缓和曲线常数:(1)缓和曲线切线角β——即HY(或YH)点的切线与ZH(或HZ)点切线的交角;亦即圆曲线一端延长部分所对应的圆心角。
目录第一部分:坐标放样竞赛题目
第二部分:缓和曲线基本知识点讲解第三部分:根据例题来计算
第四部分:自己做练习
第一部分:坐标放样竞赛题目
工程施工放样竞赛样题
已知某道路曲线第一切线上控制点ZD1(500,500)和JD1(750,750),该曲线设计半径R=1000m,缓和曲线长L0=100m,JD1里程为DK1+300,转向角α右=23°03′38″。
请按细则要求使用非程序型函数计算器计算道路曲线主点ZH、HY、QZ点坐标,及第一缓和曲线和圆曲线上中桩点K1+100、K1+280的坐标,共计算5个点。
然后,根据现场已知测站点O、定向点A、定向检核点B,使用全站仪进行第一缓和曲线和圆曲线上中桩点放样K1+100和K1+280点。
控制点和待放样曲线之间关系如图所示。
已知点有两套坐标,第一套坐标供放样,第二套坐标供检测(该套坐标放样完成后需检测时,请选手向裁判索要)。
实施步骤:
(1)计算道路曲线常数、曲线要素、主点里程、主点及若干曲线中桩点坐标;
(2)在测站点安置全站仪,定向,测量方向检核点的坐标,对定向方向进行检核;
(3)根据计算出的中桩点坐标,用全站仪点进行曲线中桩点实地放样,并在地面上做好标记;
(4)在放样点上安置棱镜等待裁判实测已放样点位坐标确定点位放样的精度。
曲线常数、要素、主点里程及中桩坐标计算成果表
第二部分:缓和曲线基本知识点讲解
铁路、公路在线路方向改变时,在转向处需要用曲线将两直线连接起来,常见的曲线形式有圆曲线、缓和曲线等。
圆曲线是具有一定半径的圆弧。
缓和曲线是曲率半径从无穷大逐渐变到圆曲线半径R。
下图为缓和曲线的图示:
一、缓和曲线的主点:直缓点ZH、缓圆点HY、曲中点QZ、圆缓点YH、缓直点HZ。
解释:直缓点表示由直线过度到缓和曲线的点。
字母是汉语拼音的首字母。
其他点同理。
二、缓和曲线常数:
(1)缓和曲线切线角β——即HY(或YH)点的切线与ZH(或HZ)点切线的交角;亦即圆曲线一端延长部分所对应的圆心角。
(2)切垂距m——即ZH(或HZ)到圆心O向切线所作垂线垂足的距离。
(3)内移距p——为垂线长与圆曲线半径R之差。
三、缓和曲线要素:
(1)切线长T:
(2)曲线长:L
(3)外矢距:E0
(4)切曲差:q
四、里程:
第三部分:根据例题来计算
工程施工放样详细教案
任务描述:
使用非编程计算器计算缓和曲线常数、曲线要素、曲线主点坐标及里程、指定放样点坐标。
然后根据已知测站点、定向点和检核点,使用全站仪放样功能进行指定中桩点放样。
放样完成后,须在测站点重新安置仪器,后视检核点,实测放样点位坐标与理论坐标进行比较。
一、计算数据
已知条件:
JD坐标:(X JD,Y JD)、ZD坐标:(X ZD,Y ZD),偏角(转角):α,曲线半径:R,缓和曲线长:l0,交点里程:JD里程
待求项目:
1.缓和曲线常数:缓和曲线切线角β、切垂距m、内移距p
2.曲线要素:切线长T、曲线长L、外矢距E0、切曲差q
3.曲线主点里程和坐标:直缓点ZH、缓圆点HY、曲中点QZ
4.放样点坐标:第一缓和曲线和圆曲线上指定中桩点各1个
计算过程:
1.缓和曲线常数
(1)缓和曲线切线角β——即HY(或YH)点的切线与ZH(或HZ)点切线的交角;亦即圆曲线一端延长部分所对应的圆心角。
计算器输入:l0×90°÷R÷π=
注意:所有待求项目在计算得到结果的同时,用铅笔记入《工程施工放样成果表》。
(2)切垂距m——即ZH(或HZ)到圆心O向切线所作垂线垂足的距离。
计算器输入:l0÷2-l03÷240÷R2=
注意:计算器的高次方输入方法为x^n。
例如:R4,计算器中应输入R^4。
另外,-1、1/2、1/3、2、3次方,计算器中均有专门按键。
(3)内移距p——为垂线长与圆曲线半径R之差。
计算器输入:l02÷24÷R=
2.曲线要素
(1)切线长:
计算器输入:(R+p)×tan(α÷2)+m=
注意:偏角(转角)α,不论右偏还是左偏,其数值均取正值。
公式中,如果右偏、左偏有影响,会通过正负系数ξ考虑。
(2)曲线长:
计算器输入:R×α×π÷180°+l0=
(3)外矢距:
计算器输入:(R+p)÷cos(α÷2)-R=
(4)切曲差:
计算器输入:2×T-L=
3.曲线主点里程
(1)
(2)
(3)
(4)
(5)
注意:里程直接以米为单位写数值,写成DK***+***.****的形式。
例如:起点里程为DK497+600.000,计算过程、结果均写作497600.000。
所有结果均保留到小数点后三位,角度保留到计算器显示位数。
4.坐标计算(弦长弦切角法)
(1)根据已知点ZD、JD的坐标,作出这两个已知点的相对位置草图。
(2)第一条切线(ZD-JD)的坐标方位角:
(此知识点再讲)
计算器输入:tan-1((Y JD-Y ZD)÷(X JD-X ZD))=
(3)计算ZH坐标:
(4)计算缓和曲线上待求点i的坐标(中线桩1、HY)——直接使用弦长公式
待求点i到ZH间曲线长:
待求点i的放样直角坐标:
计算器输入:
(5)计算步骤
先分别计算l1、l H
中线桩1:
HY:
再输入X1公式,求X1得后,按计算器向左键“⊲”,修改X1公式为Y1公式,依次求得Y1、Y HY、X HY。
(6)计算圆曲线上待求点j的坐标(中线桩2、QZ)
待求点j到HY间曲线长:
待求点j的放样直角坐标:
计算器输入:
(7)计算步骤
先分别计算l2、l Q
中线桩2:
QZ:
再输入X2公式,求X2得后,按计算器向左键“⊲”,修改X2公式为Y2公式,依次求得Y2、Y QZ、X QZ。
注意:
①arctan(*),计算器中应输入tan-1(*);先按SHIFT键,后按tan 键,即可调用。
③α为偏角(转角),不论右偏还是左偏,其数值均取正值。
④ξ为曲线右左偏影响系数,右偏时,取1;左偏时,取-1。
5.简明计算公式
(1)缓和曲线切线角:
(2)切垂距:
(3)内移距:
(4)切线长:
(5)曲线长:
(6)外矢距:
(7)切曲差:
(8)
(9)
(10)
(11)
(12)
(13)第一条切线(ZD-JD)的坐标方位角:(14、15)计算ZH坐标:
(16-18)计算缓和曲线上待求点i的坐标(中线桩1、HY)——直接使用弦长公式
待求点i到ZH间曲线长:
待求点i的放样直角坐标:
(19-21)计算圆曲线上待求点j的坐标(中线桩2、QZ)待求点j到HY间曲线长:
待求点j的放样直角坐标:
第四部分:自己做练习
根据例题的讲解,把竞赛的题目算完。