带缓和曲线放样数据计算

用全站仪进行缓和曲线各主点坐标放样的计算利用全站仪进行缓和曲线各主点坐标放样,关键的问题就在于如何计算出各主点的坐标。

下面就来讨论一下各主点坐标的计算方法。

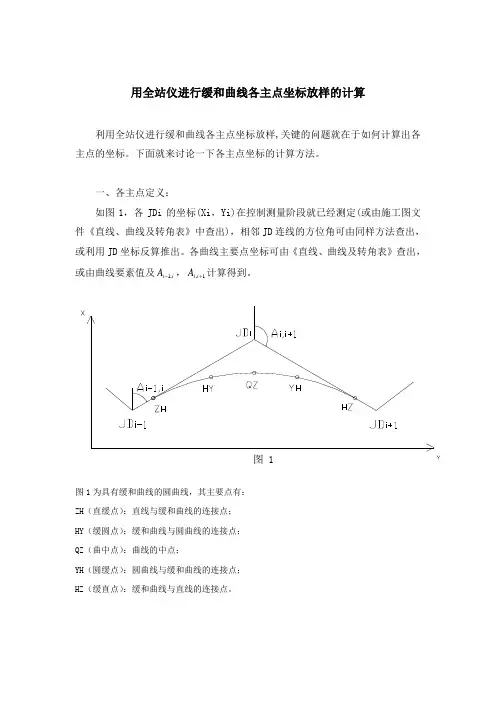
一、各主点定义：如图1，各JDi 的坐标(Xi ，Yi)在控制测量阶段就已经测定(或由施工图文件《直线、曲线及转角表》中查出)，相邻JD 连线的方位角可由同样方法查出，或利用JD 坐标反算推出。

各曲线主要点坐标可由《直线、曲线及转角表》查出，或由曲线要素值及i i A ,1-，1,+i i A 计算得到。

图 1图1为具有缓和曲线的圆曲线，其主要点有：ZH （直缓点）：直线与缓和曲线的连接点；HY （缓圆点）：缓和曲线与圆曲线的连接点；QZ （曲中点）：曲线的中点；YH （圆缓点）：圆曲线与缓和曲线的连接点；HZ （缓直点）：缓和曲线与直线的连接点。

二、各主点的坐标计算1. 当P 点位于带缓和曲线的圆曲线时，又分为以下三种情况：1.1 ZH 到HY 段)30cos(2,10Si i p RL l A c x x π±⨯+=- )30sin(2,10si i p RL l A cy y π±⨯+=-式中 22590sL R l l c -=)(0,0y x 为ZH 点坐标l 为P 点与ZH 点桩号差s L 为缓和曲线长当路线左转时，取“-”，反之取“+”1.2 HY 到YH 段)9090cos(90sin 2,10R L R l A R lR x x si i p πππ±±+=-)9090sin(90sin 2,10R L R l A R l R y y si i p πππ±±+=-式中 )(0,0y x 为HY 点坐标l 为P 点与ZH 点桩号差s L 为缓和曲线长当路线左转时，取“-”，反之取“+”1.3 HZ 到YH 段)30180cos(21,0Si i p RL l A c x x π±+⨯+=+)30180sin(21,0S i i p RL l A c y y π±+⨯+=+式中，22590s L R l l c -=)(0,0y x 为HZ 点坐标l 为HZ 点与P 点的桩号差当路线左转时，取“+”，反之取“-”三、计算示例已知JD9（x = 2006，y = 2007），JD10（x = 2250，y = 3140），JD11（x = 1865，y = 4250）JD10里程 K16 + 062.25 ，m R 2500= m L S 300=求： 各主点（ZH 、HY 、QZ 、YH 、HZ ）坐标；解：1、 （通过坐标反算）得出：A9，10 = 77°50′47.56″ D9，10 = 1158.976 mA10，11 = 109°07′44.19″ D10，11 = 1174.872 m路线转角 y α = 109°07′44.19″ - 77°50′47.56″= 31°16′56.63″2、计算出各曲线要素值：（加设缓和曲线后，圆曲线相对于切线的内移量）=p R Ls 242 = 2500243002⨯ = 1.5 m （缓和曲线角度） =0β RLs 2×ρ = 300/（2×2500）× 206265 = 12375.9 = 3°26′15.89″（加设缓和曲线后，切线增长值）m = 2Ls - 23240R Ls = 2300 - 25002500240300300300⨯⨯⨯⨯ = 150 - 0.018 = 149.982 m（切 线 长） )(p R m T ++=×tg 2yα= 149.982 + (2500+1.5)×tg 256.631631"'︒ = 149.982 + 2501.5 ×tg(15°38′28.32″)= 149.982 + 2501.5×0.27998= 850.353 m（曲线长） =L 001802-(）βαπy R ⨯ + 2s L = 018015.892632-56.63163125001416.3）（"'︒⨯"'︒⨯⨯ + 2×300 = 7854×0.1356 + 600 = 1664.954 m（外 矢 距） E = ( R +p ) sec2y α - R = (2500+1.5)sec 256.631631"'︒ - 2500 = 2501.5 × sec( 15°38′28.32″) – 2500 = 2501.5 × 1.0384 – 2500= 97.695 m（切 曲 差） L -T 2⨯=q = 2×850.353 - 1664.954= 1700.706 - 1664.954 = 35.752 m3、 由于JD10里程为K16+062.250，所以各主点里程为ZH K15+211.897 （K16+062.250–T = K16+062.250 - 850.353）HY K15+511.897 （K15+211.897 + Ls = K15+211.897 + 300.000）HZ K16+876.851 （K15+211.897 + L = K15+211.897 + 1664.954）YH K16+576.851 （K16+876.851 - Ls = K16+876.851 - 300.000）QZ K16+044.374 = (K16+576.851 + K15+511.897 ) / 24、各主点坐标计算如下：4.1. ZH 点 由已知条件：897.521125.6062,3140,225000-===l Y X 和 =-i i A ,1 257°50′47.56″ 代入公式i i p A l x x ,10cos -+=i i p A l y y ,10sin -+= 式中 )(0,0y x 为该段直线的起点（JD10）坐标l 为要求的P 点与该段直线起点的桩号差（距离）得： X = 2070.974 Y = 2308.7062. HY 点 由已知条件：300,706.2308,975.207000====S L l Y X 和 =-i i A ,1 77°50′47.56″ 代入公式（3），得 X=2128.246 Y=2603.1393. QZ 点 由已知条件：954.1664,139.2603,246.212800===l Y X 和 =-i i A ,177°50′47.56″ 代入公式（4），得 X=2152.482 Y=3134.1084. HZ 点 由已知条件：353.850,3140,225000===l Y X 和=+1,i i A 109°07′44.19″ 代入公式（1），得 X=1971.339 Y=3943.8855. YH 点 由已知条件：300,885.3943,339.197100====S L l Y X 和 =+1,i i A 109°07′44.19″ 代入公式（5），得 X=2063.945 Y=3658.5866. 复核 QZ 点，由已知条件：=+1,i i A 109°07′44.19″和300,477.532,586.3658,945.206300====S L l Y X代人公式（4）得 X=2152.538 Y=3134.014与第3步的QZ 计算结果比较得坐标闭合差：δx = 0.056 δy = -0.004 根据坐标闭合差计算距离闭合差：s f = y y x ＋x δδδδ = 0.0561则相对闭合差： k = 0.0561/1664.954 = 1/29678查得国家一级导线闭合差容许值： k 容 ≤ 1/15000 因为k 符合k 容，所以取两次计算值的平均数为最后结果，即 X=2152.510 Y=3134.061四、结束语缓和曲线各主点的坐标计算问题是实际工程中的最基本问题，只要算出各主点的坐标，用全站仪在实地进行坐标放样就非常方便了。

b0
20
ls 3R
此外还有极坐标法、弦线支距法、长弦偏角 法。
缓和曲线的计算方法三种
要注意：点是位于缓和曲线上，还是位于圆曲线上。
位于缓和曲线
位于圆曲线
缓和曲线的计算方法三种
（1）当点位于缓和曲线上，有：
x y
l l5
40
R
2
l
2 s
l3 l7 6 Rl s 336 R
3l
3 s
（2）当点位于圆曲线上，有：
xRsinq yR(1c os)p
缓和曲线的计算方法三种
2、偏角法（整桩距、短弦偏角法） 要注意：点是位于缓和曲线，还是位于圆曲线。
位于圆曲线 位于缓和曲线
缓和曲线的计算方法三种
2、偏角法（整桩距、短弦偏角法）
（1）当点位于缓和曲线上，有：
总偏(常 角量 )0 6lR s
偏角
l2 ls2
0
距离：用曲线长l来代替弦长。放样出第1点后， 放样第2点时，用偏角和距离l交会得到。
缓和曲线的计算方法三种
（2）当点位于圆曲线上
方法：架仪HY (或YH)，后视ZH(或HZ)，拨角b0，即找 到了切线方向，再按单圆曲线偏角法进行。
缓和曲线的计算方法三种
（2）测设方法。(见例题)
例题：如图，设某公路的交点桩号为K0+518.66，右 转角αy=180018'36"，圆曲线半径R=100m，缓和曲 线长ls=10m，试测设主点桩。（作为实习课内容）
解：（一）计算测设元素
p=0.04m；q=5.00m；
02lR s 1800205153
缓和曲线的计算方法三种
2、回旋缓和曲线(spiral curve)基本公式

收稿日期:2005-08-04作者简介:王新民, 男, 济南城建工程公司工程师。

带有缓和曲线的圆曲线放样新方法王新民1, 张祥龙2(1、济南城建工程公司, 山东济南250031; 2、山东广播电视大学, 山东济南250014摘要:传统的曲线放样方法由于经常受施工现场地形、交通等条件的限制而无法进行, 而利用全站仪按坐标放样的方法可灵活解决以上难题。

本文以切线支距法测设曲线的计算公式为基础, 通过坐标转换, 导出了曲线上任一点在城市统一坐标系坐标的计算公式, 并结合工程实践总结了利用全站仪放样曲线的优越性。

关键词:缓和曲线; 圆曲线; 坐标法; 坐标转换; 曲线放样中图分类号:TU 198文献标识码:A 文章编号:1008-3340(2006 01-0071-02道路曲线放样的传统方法主要有偏角法、切线支距法、弦线偏距法等, 这些方法通常是将仪器架设在曲线的起点、终点或其它要素点进行测设, 适用于地势平坦地区, 通视条件好且易于量距, 但遇到丘陵地区或者线路跨沟过河等情况就行不通。

随着全站仪在工程测量中的普及应用, 一种新的曲线放样方法──坐标法[2]在工程实践中得到了广泛的应用。

这种方法是先计算出曲线上任意点的城市统一坐标系坐标, 然后利用导线点用极坐标法现场放样[3]。

1曲线坐标计算 1. 1坐标系的建立首先假定一个独立曲线坐标系。

如图1所示, 建立以ZH 点为坐标原点, 过该点切线为x 轴, 法线方向为y 轴的曲线坐标系。

1. 2曲线起终点坐标计算设计部门一般给出曲线交点(J D 的城市坐标及其方位角θ, 曲线起点(ZH 、终点(HZ 坐标若未给出, 则可由JD 根据设计曲线参数(T h 、α 很容易推算出来。

1. 3缓和曲线上任意一点坐标计算缓和曲线上任意一点N 的曲线坐标系坐标(x n , y n 的计算公式[1]:x n =l n -l 5S 40R 2l 2S y n l 36R l S(1式中:l n -曲线上任一点N 到ZH 点的曲线长度(里程差;l s -缓和曲线长度;R -缓和曲线终点的圆曲线半径。

程序使用说明Fx9750、9860系列程序包含内容介绍:程序共有24个，分别是：1、0XZJSCX2、1QXJSFY3、2GCJSFY4、3ZDJSFY5、4ZDGCJS6、5SPJSFY7、5ZDSPFY8、5ZXSPFY9、6ZPJSFY 10、7ZBZFS 11、8JLHFJH 12、9DBXMJJS13、9DXPCJS 14、9SZPCJS 15、GC-PQX 16、GC-SQX17、PQX-FS 18、PQX-ZS 19、ZD-FS 20、ZD-PQX21、ZD-SQX 22、ZD-ZS 23、ZDSP-SJK 24、ZXSP-SJK其中，程序2-14为主程序，程序15-24为子程序。

每个主程序都可以单独运算并得到结果，子程序不能单独运行，它是配合主程序运行所必需的程序。

刷坡数据库未采用串列，因为知道了窍门，数据库看起很多，其实很少。

程序1为调度2-8程序；程序2为交点法主线路(含不对称曲线)中边桩坐标正反计算及极坐标放样程序；程序3为主线路中边桩高程计算及路基抄平程序；程序4为线元法匝道中边桩坐标正反计算及极坐标放样程序；程序5为匝道线路中边桩高程计算及路基抄平程序；程序6为任意线型开口线及填筑边线计算放样程序；程序7专为主线路开口线及填筑边线计算放样程序，只需测量任意一点三维数据，即可马上计算出该点相对于中桩法线上的偏移量；程序8专为匝道线路开口线及填筑边线计算放样程序，只需测量任意一点三维数据，即可马上计算出该点相对于中桩法线上的偏移量；程序9为桥台锥坡计算放样程序；程序10为计算两点间的坐标正反算程序；程序11为距离后方交会计算测站坐标程序；程序12为任意多边形面积周长计算程序；程序13为导线近似平差计算程序；程序14为水准近似平差计算程序；程序2-8所用数据库采用的串列，匝道用的File 1；主线用的File 2。

第一步：先用Excel按照文字说明输入完整条线路对应数据；第二步：保存为CSV格式，然后设置单元格格式、数字格式、科学计数、小数位数设置10位以上并保存；第三步：用FA-124导入，匝道数据列表文件选择“File 1”，主线数据列表文件选择“File 2”。

缓和曲线的数学公式：
x=l-l5/40R2l05+l9/3456R4l04 y=l3/6Rl0-l7/336R3l03+l11/42240R5l05 式中：x、y 为以缓和曲线起点（ZH）为坐标原点，以缓和曲线 起点切线方向为 x 轴，过缓和曲线起点垂直于切线方向为 y 轴建 立的坐标系，任一曲线长 l 处的点在该直角坐标系的 x、y 坐标 （如图 1）；R 为圆曲线半径，l0 为整条缓和曲线的长度（l0=Khy-K0， Khy 为 HY 点处的桩号）。这样就很容易计算出缓和曲线的直角坐 标了，然而实际工作中还必须把相对坐标 x、y 化成绝对大地坐标 X、Y，而且还必须计算曲线上任意一点的法线方向的某一点的大 地坐标 X、Y（如垂直或斜交公路的桥梁、涵洞的中心线），计算方 法如下：如图 3 设进入直缓点 ZH 前直线段的方位角为 T0，ZH 点 的大地坐标为 X0，Y0。 （1）先计算在缓和曲线坐标系相对坐标 x、y 坐标：
榆如此反复，直到 Sn=M（H-Hn）为止，得到的点即为 ON 点。
3 结束语
X 左=X+D 左 cos（T0依A-90） Y 左=Y+D 左 sin（T0依A-90） X 右=X+D 右 cos（T0依A+90） Y 右=Y+D 右 sin（T0依A+90） 注：淤D 左、D 右为法线上的左边或右边的点至中心点的距离。 于A 前“依”号前进方向右转为依左转为-。盂如果不是正交那么用
x=l-l5/40R2l05+l9/3456R4l04 y=l3/6Rl0-l7/336R3l03+l11/42240R5l05 （2）再计算曲线上任意长 l 处的点大地坐标 X、Y： X=X0+xcosT0+ycos（T0依90） Y=Y0+xsinT0+ysin（T0依90）（前进方向右转为+左转为-） （3）计算缓和曲线上任意长 l 处的点切线偏角 A： A=l2伊180/2伊仪伊R伊l（0 l=K-K0，K 为里程桩号）

缓和曲线的计算随着公路交通事业的发展,高等级公路将成为未来公路发展的主流。

在高等级公路中勘测和设计人员为了提高线型标准,普遍采用了以曲线为主的平面线型,设计图一般只给出了路线的有关参数和施工图,测量人员需要根据具体的路线里程和施工图进行再计算,计算出坐标用仪器放样,因此本文首先讨论缓和曲线任一点坐标的计算工地的施工放样。

1．缓和曲线的作用1）便于驾驶员操纵方向盘2）乘客的舒适与稳定，减小离心力变化3）满足超高、加宽缓和段的过渡，利于平稳行车4）与圆曲线配合得当，增加线形美观2．回旋线基本方程:即用回旋线作为缓和曲线的数学模型。

令：ρ=R，Ls=s 则 Ls=A2/R3．直角坐标及要素计算1）回旋线切线角（1）缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。

βx=L2/2RL s（2）缓和曲线的总切线角β=L s /2R.180/л2）缓和曲线直角坐标任意一点P 处取一微分弧段ds ，其所对应的中心角为d βxdx=dscos βxdy=dssin βx3）缓和曲线常数（1）主曲线的内移值p 及切线增长值q内移值：p=Y h -R(1-cosβh )=Ls 2/24R切线增长值：q=X h -Rsinβh =Ls/2-Ls 3/240R 2（2）缓和曲线的总偏角及总弦长总偏角：βh =Ls/2R总弦长：C h =Ls-Ls 3/90R 24）缓和曲线要素计算《公路工程技术标准》规定，当R<R 免时，必须设置缓和曲线。

切线长()q a p R q T T h ++=+=2tan 外距 ()R a p R p E E h -+=+=2sec 曲线长 ()s s 18022180l aR l a R L h +=+-=πβπ圆曲线长 s 2l L L h y -=切线差 h h h L T D -=2平曲线五个基本桩号：ZH——HY——QZ——YH——HZ5、坐标计算1)如图1建立以ZH为坐标原点,过ZH点的缓和曲线切线为X轴, ZH点上缓和曲线的半径为Y轴的直角坐标系。

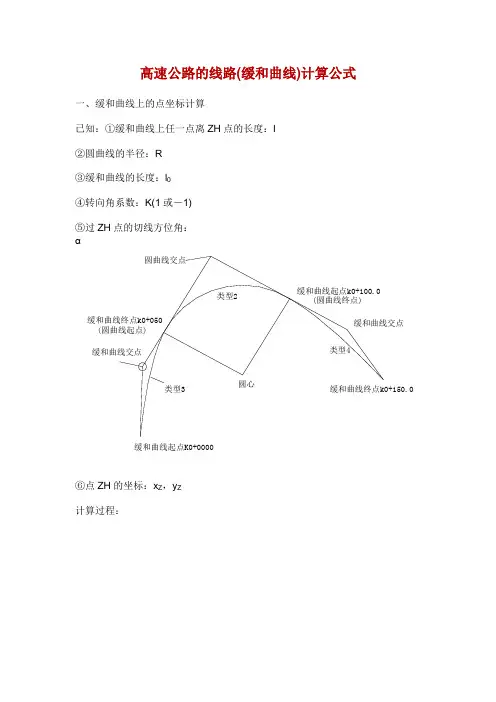
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y ②待求点的切线方位角：αT计算过程：。

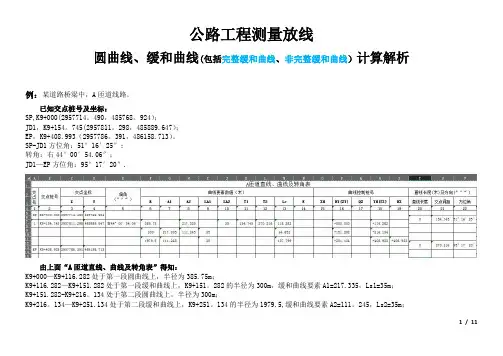
公路工程测量放线圆曲线、缓和曲线(包括完整缓和曲线、非完整缓和曲线）计算解析例：某道路桥梁中，A匝道线路。

已知交点桩号及坐标：SP,K9+000(2957714。

490，485768。

924）；JD1，K9+154。

745(2957811。

298，485889.647）；EP，K9+408.993（2957786。

391，486158.713）。

SP-JD1方位角：51°16′25″;转角：右44°00′54.06″；JD1—EP方位角：95°17′20″.由上面“A匝道直线、曲线及转角表”得知：K9+000—K9+116.282处于第一段圆曲线上，半径为385.75m；K9+116.282—K9+151.282处于第一段缓和曲线上，K9+151。

282的半径为300m，缓和曲线要素A1=217.335，Ls1=35m；K9+151.282-K9+216。

134处于第二段圆曲线上，半径为300m；K9+216。

134—K9+251.134处于第二段缓和曲线上，K9+251。

134的半径为1979.5,缓和曲线要素A2=111。

245，Ls2=35m；1 / 11K9+251。

134—K9+408.933处于第三段圆曲线上，半径为1979。

5m。

求：K9+130、K9+200、K9+230、K9+300的中桩坐标，切线方位角,左5米边桩的坐标，右10米边桩的坐标。

解：首先，我们知道要求一个未知点的坐标，必须知道起算点坐标，起算点至未知点的方位角，起算点至未知点的直线距离,然后利用坐标正算的计算公式，就可以直接求出未知点的坐标.那么，关于圆曲线和缓和曲线（包括完整缓和曲线和非完整缓和曲线）的计算，我们需要知道如何求出起算点至圆曲线或缓和曲线上某点的方位角和直线距离.下面，先列出关于圆曲线和缓和曲线中角度和距离计算的相关公式。

2 / 113 / 11y 轴。

过圆曲线上任意点P 的切线与ZY-JD 相交，夹角（切线角）为β，ZY-P 与ZY —JD 的夹角（弦切角）为α，ZY-P 的弧长为L ，ZY —P 的直线距离为d,圆曲线的半径为R 。

缓和曲线常数既有线元素，又有角元 素，且均 为圆曲
线半径
R 和缓和曲线长
l0 的函数。线元素要计算到 mm，角元素要计算到秒。
二、缓和曲线综合要素
切线长：T = (R + P)tan⎜⎛α ⎟⎞ + m
⎝2⎠
曲线长： L = R(α − 2β0 ) + 2l0
外视距： E0
=
R+P cos⎜⎛α ⎟⎞
垂线方向和到 B 的半径方向所形成的 圆心角，按下式计算:
αb
=
lb
− l0 R
+ β0
δβ
=
1 6Rl0
(lT
− lB )(lB
+ 2lT )
=
30 πRl0
(lT
−
lB )(lB
+
2lT
)
δt
=
lt2 6Rl0
= 30lt2 πRl0
βt
=
lt2 2Rl0
= 90lt2 πRl0
bt
=
lt2 3 Rl 0
lT — 为置镜点的缓和曲线长； lF — 为远离 ZH(HZ)点的缓和曲线长。
五、直角坐标法
1、缓和曲线参数方程：
xa
=
la
−
1 40 R 2l02
la5
ya
=
1 6Rl0
la3
−
la7 336R3l03
2、圆曲线
xb = R sinαb + m
yb = R(1 − cosα b ) + P
式中，αb 为圆心 O 到切线的
−
R
⎝2⎠
切曲差： q = 2T − L

JD1
Y O
X ZHi X JDi1 (Si1,i Ti ) cos αi1,i YZHi YJDi1 (Si1,i Ti ) sin αi1,i
X
起点
ZY1
QZ2 YZ1
JD2
ZH2
HY2 QZ2 YH2 HZ2
终点
JD1
Y
O
X HZi1 X JDi1 Ti1 cos i1,i
YHZi1 YJDi1 Ti1 sin i1,i
（二）曲线上桩点坐标的计算
1、计算切线坐标 （1）ZH～HY段
xi
li
li5 40R 2l2
yi
li3 6Rl
式中： li —— 缓和曲线上任意一点 i 到直缓点的弧长。
2、HY～YH段
xi R sin i m
yi R 1 cosi p
（四）缓和曲线常数计算
缓和曲线的常数包括：缓和曲线切线角o 、切垂距
（切线增长值）m 、内移距 p。
➢ 缓和曲线切线角o —— 过 HY（或YH）点的 切线与ZH（或HZ）点的切线组成的角。即圆曲线
被缓和曲线所代替的那一段弧长对应的圆心角。 ➢ 切垂距 m —— 由圆心向切线作垂线的垂足到 缓和曲线起点的距离。 ➢ 内移距 p —— 加缓和曲线后，圆曲线相对于 切线的内移量。
=∞Biblioteka 在与圆曲线相接处，l = lo ， 等
于圆曲线半径 R，则 c = R×lo。
直线
lo —— 缓和曲线总长。
=R
圆曲线
（二）缓和曲线方程式
回旋曲线（辐射螺旋线） 的方程式为：
x
l
l5 40R 2l2
l9 3456R 4l4
y
l3 6Rl

随着计算机技术和 GIS技术的发展以及应用需求的不 断深入 ,管线信息系统 ,通过广泛集成 GIS技术 、GPS技术 、 多媒体技术 、CAD技术及人工智能技术 ,从进行城市地下管 线的采集 、管理 、综合分析与处理的技术系统向功能强大的
空间决策支持系统或专家系统发展将成为一种趋势 。不断 完善的管线信息系统必将发挥越来越重要的作用 。 参考文献 [ 1 ]曹瑜 ,胡光道. 地理信息系统在国内外应用现状 [ J ]. 计算机与现
要做好一件事情 ,自信心是至关重要的 。教师在教学中 能否培养学生的自信心 ,也是教学成功与否的关键 。教师在 教学中如果对学生的点滴进步能够加以肯定和鼓励 ,就会使 学生充满信心 ,使学生感到成功感 。例如 ,在短跑的教学中 , 对一些身体素质差的同学 ,在训练时 ,假如学生都认真投入 地训练 ,哪怕没有进步 ,我们也要加以鼓励 ,然后再进行动作 技术上的改正 ,测验时 ,我们区别对待 ,鼓励那些经过努力又
·28·
第 3期
李金生等 :曲线放样数据计算的几种方法
图 2 缓和曲线示意图 1. 1. 1 圆曲线细部点的直角坐标公式
如图 1所示为一段单圆曲线 ,建立以 ZY点为原点 ,切线方向为 X轴 ,过 ZY点的半径方向为 Y轴的假定直角坐标系 ,则曲线上各细 部点的直角坐标可以表示为 :
xi = R sinφi yi = R ( 1 - cosφi ) 其中圆心角 φi可以表示为 li /R, li是细部点 i到曲线起点 ( ZY) 点的曲线长度 。代入上式得 :
摘 要 曲线测设是公路 、铁路 、管线等线状工程技术设计 、施工放样的主要内容之一 ,是工程测量人员日常 工作的主要组成部分 ,曲线放样数据计算的方法多种多样 ,本文主要讨论曲线放样数据计算的几种常用方法 ,并 比较其特点及各自适用条件 。

内输 出准 确 的 Ｋ值 和 该 点距 中桩 线 的距 离 ； 如果 不在 阈值 以 内 ， 返 回调 用 数据 库 的位 置 ，重新 进 行 计算 ，直 到在 阈值 以 内后 ，输 出准 确 的 Ｋ值和 该 点距 中桩 线 的距 离 。 这 就完 成 了缓 和 曲线 平 面
位 置 的求 解 。下 面 为计 算 流 程 图 。 式 中 的 ０为 ：
两 侧 。实 际地 形 中 ，路 线 是不 规 则 的 ，车 辆 在行
驶过程 中， 受 到 做 圆周 运 动 的影 响 ，会 产 生 向外 的离 心 力 。路基 宽度 的坡 比必 须 随 之产 生变 化 ，
图 ５ ． ２ 加 宽过 渡 示 意 图
以使 车 辆 在运 动 中保 持 平衡 。
到加 宽值 在 路 线 的 左边 还 是 右 边 ， 首 先 计 算 没 有
加 宽 的 一边 ， 以坡 比 ａ 、ｃ 、变 化 的 终值 ｂ和 距
离Ｌ 、Ｌ 。 推 算 出该 点位 置 的 实 际高 程 ，在 有 加 宽
的一 边 参 照 图 ４ ． １的变 化 过程 ， 得 到有 加 宽 一 边 的高 程 。需要 特 别 指 出 的 是 ，加 宽 的 宽度 依 据 图
② 从 准 备 好 的数 据 库 中调 用 己知 的量 （ 某 一
段 缓 和 曲线起 点 桩 、 终点桩号、 圆 曲线 的斜 坡 率 、
② 然 后 根据 圆 曲线 的半径 大 小 ， 缓 和 曲线 内 侧 和 外 侧 以相 同 的坡 比 进 行 变 化 到 一 个 固 定 值
ｂ。
缓 和 曲线 的长度 、加 宽 的 长度 、判 断 缓和 曲线 转 向的判 定 值 等 ） ，用 这 些 已知 量 分 段解 算 横 断面

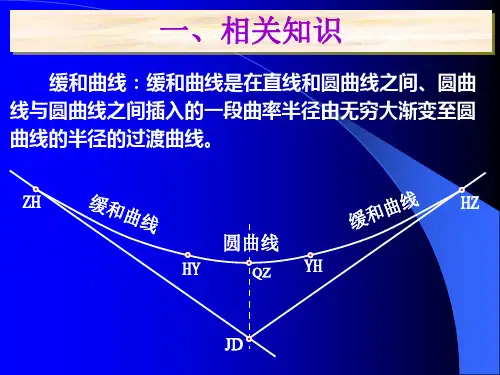
缓和曲线的计算步骤在缓和曲线的计算中，首先要判断缓和曲线的完整性。

判断公式为L 0=C/R上式中，L 0为缓和曲线的计算长度，C 为缓和曲线参数，C ＝A 2，A 也是缓和曲线的一个参数，R 为设计给的缓和曲线起、终点半径中的最小值。

若计算出来的L 0与设计给的缓和曲线长度l 一样，那么该曲线即是完整的，若L 0比设计给的缓和曲线长度要大，那么设计给的缓和曲线就不是完整的。

下面就完整缓和曲线与不完整缓和曲线的计算方法作一个说明。

一、完整缓和曲线的计算方法：完整缓和曲线有一个特征，就是它的起点或终点半径中有一个是无穷大（该点不是ZH 点就一定是HZ 点），我们称的“缓和曲线起点”就从这个半径为无穷大的点开始的。

计算过程如下：1、根据交点（JD ）的桩号推求直缓点、缓圆点、曲中点、圆缓点、缓直点的桩号。

有时设计已经给出这些数据。

2、 建立切线坐标系，求曲线中线点的切线坐标。

切线坐标系，即以ZH 点（或HZ ）为原点、以该点切线方向为X1轴的坐标系。

为了使第一缓和曲线和第二缓和曲线具有通式，我们在ZH 点和HZ 点采用同样的左手坐标系（图1）。

在缓和曲线段，中线点切线坐标X 1=l -l 5/40C 2+l 9/3456C 4+…Y 1=l 3/6C- l 7/336C 3+l 11/42240C 5+…(1)式中 l 为ZH 或HZ 至所求点的曲线长。

(1)式是第一缓和曲线和第二缓和曲线的计算通式，仅注意在计算第二缓和曲线时计算的方向相反，C 的符号也相反。

在通常情况下，（1）式取前两项即可满足精度要求；但是当曲线半径过小时，必须顾及第三项，例如匝道或试车场以及山区公路可能有这种情况。

3、将中线点的切线坐标转换为施工测量坐标系坐标一条公路（或工程工地）往往采取统一的施工测量坐标系。

我们必须将曲线中线点的切 线坐标X 1 、Y 1，通过平移和旋转转换为施工测量坐标系坐标X 、Y 。

转换公式如下： 将上式展开，即是：X ＝X 0+X 1COSA 0－Y 1SINA 0Y ＝Y 0+X 1 SINA 0+Y 1 COSA 0(2)式中 ：A 0是过ZH 点的切线方位角，或HZ 点的切线方位角加减180°；X 0、Y 0为ZH 或HZ 的施工测量系坐标。

高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R 2——曲线终点处的半径P——曲线起点处的曲率1——曲线终点处的曲率P2α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i(上坡为“＋”，下坡为“－”)1(上坡为“＋”，下坡为“－”)②第二坡度：i2③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K③曲线终点桩号：K1④曲线起点坐标：x0，y⑤曲线起点切线方位角：α⑥曲线起点处曲率：P(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：。

四公司沿海项目部李洪亮摘要：利用一缓和曲线算例，通过数学分析，推导出缓和曲线逐桩坐标计算公式，此公式可作为道路测设中的范例来运用，有很强的指导意义。

关键词：缓和曲线、公式、逐桩坐标一、引言道路建设中，由于受地形或地质影响，经常需要改变线路方向，为满足行车要求，往往要用曲线把两条直线连接起来。

曲线的构成形式无外乎圆曲线和缓和曲线，本文以河北省沿海高速某曲线段为例推导出缓和曲线的逐桩坐标计算公式，以方便图纸的审核，满足施工放样的需求。

本公式具有良好的操作性，方便施工、提高精度，可作为道路测设中的范例运用。

二、公式推导1 、实例数据河北省沿海高速公路一缓和曲线（如图）： AB 段为缓和曲线段， A 为 ZH 点，B 为 HY 点， RB =800m ； A 点里程为 NK0+080 ，切线方位角为θA=100 ° 00 ′24.1 ″，坐标为 XA =4355189.493,YA=476976.267 ； B 点里程为 NK0+158.125 ，切线方位角为θB =102 ° 48 ′ 15.6 ″，坐标为 XB=4355174.669 ，YB=477052.964 ，推求此曲线段内任意点坐标。

2 、公式推导及实例计算方法一：弦线偏角法1 ）公式推导由坐标增量的计算方法我们不难理解，求一点坐标可以根据其所在直线的方位角以及直线上另一点的坐标和距待求点的距离。

所以我们可以利用 ZH 点，只要知道待求点距 ZH 点的距离（弦长 S ）和此弦与 ZH 点切线方位角的夹角（转角a ），即可求出该点坐标。

根据回旋线方程 C=RL ，用 B 点数据推导出回旋线参数：C=RLS =800*78.125=62500 （ LS为 B 点至 ZH 点的距离）设待求点距 ZH 点距离为 L因回旋线上任意点的偏角β0=L2/2RLS, 且转角 a=β/3 ，可得该点转角 a 。

（曲线左转时 a 代负值）。

目录第一部分：坐标放样竞赛题目第二部分：缓和曲线基本知识点讲解第三部分：根据例题来计算第四部分：自己做练习第一部分：坐标放样竞赛题目工程施工放样竞赛样题已知某道路曲线第一切线上控制点ZD1<500,500>和JD1<750,750>,该曲线设计半径R=1000m,缓和曲线长L0=100m,JD1里程为DK1+300,转向角α右=23°03′38″.请按细则要求使用非程序型函数计算器计算道路曲线主点ZH、HY、QZ 点坐标,与第一缓和曲线和圆曲线上中桩点K1+100、K1+280的坐标,共计算5个点.然后,根据现场已知测站点O、定向点A、定向检核点B,使用全站仪进行第一缓和曲线和圆曲线上中桩点放样K1+100和K1+280点.控制点和待放样曲线之间关系如图所示.已知点有两套坐标,第一套坐标供放样,第二套坐标供检测〔该套坐标放样完成后需检测时,请选手向裁判索要〕.实施步骤：〔1〕计算道路曲线常数、曲线要素、主点里程、主点与若干曲线中桩点坐标；〔2〕在测站点安置全站仪,定向,测量方向检核点的坐标,对定向方向进行检核；〔3〕根据计算出的中桩点坐标,用全站仪点进行曲线中桩点实地放样,并在地面上做好标记；〔4〕在放样点上安置棱镜等待裁判实测已放样点位坐标确定点位放样的精度.曲线常数、要素、主点里程与中桩坐标计算成果表第二部分：缓和曲线基本知识点讲解铁路、公路在线路方向改变时,在转向处需要用曲线将两直线连接起来,常见的曲线形式有圆曲线、缓和曲线等.圆曲线是具有一定半径的圆弧.缓和曲线是曲率半径从无穷大逐渐变到圆曲线半径R.下图为缓和曲线的图示：一、缓和曲线的主点：直缓点ZH、缓圆点HY、曲中点QZ、圆缓点YH、缓直点HZ.解释：直缓点表示由直线过度到缓和曲线的点.字母是汉语拼音的首字母.其他点同理.二、缓和曲线常数：〔1〕缓和曲线切线角β——即HY〔或YH〕点的切线与ZH〔或HZ〕点切线的交角；亦即圆曲线一端延长部分所对应的圆心角.〔2〕切垂距m——即ZH〔或HZ〕到圆心O向切线所作垂线垂足的距离.〔3〕内移距p——为垂线长与圆曲线半径R之差.三、缓和曲线要素：〔1〕切线长T：〔2〕曲线长：L〔3〕外矢距：E0〔4〕切曲差：q四、里程：第三部分：根据例题来计算工程施工放样详细教案任务描述：使用非编程计算器计算缓和曲线常数、曲线要素、曲线主点坐标与里程、指定放样点坐标.然后根据已知测站点、定向点和检核点,使用全站仪放样功能进行指定中桩点放样.放样完成后,须在测站点重新安置仪器,后视检核点,实测放样点位坐标与理论坐标进行比较.一、计算数据已知条件：JD坐标：〔X JD,Y JD〕、ZD坐标：〔X ZD,Y ZD〕,偏角〔转角〕：α,曲线半径：R,缓和曲线长：l0,交点里程：JD里程待求项目：1.缓和曲线常数：缓和曲线切线角β、切垂距m、内移距p2.曲线要素：切线长T、曲线长L、外矢距E0、切曲差q3.曲线主点里程和坐标：直缓点ZH、缓圆点HY、曲中点QZ4.放样点坐标：第一缓和曲线和圆曲线上指定中桩点各1个计算过程：1.缓和曲线常数〔1〕缓和曲线切线角β——即HY〔或YH〕点的切线与ZH〔或HZ〕点切线的交角；亦即圆曲线一端延长部分所对应的圆心角.计算器输入：l0×90°÷R÷π=注意：所有待求项目在计算得到结果的同时,用铅笔记入《工程施工放样成果表》.〔2〕切垂距m——即ZH〔或HZ〕到圆心O向切线所作垂线垂足的距离.计算器输入：l0÷2-l03÷240÷R2=注意：计算器的高次方输入方法为x^n.例如：R4,计算器中应输入R^4.另外,-1、1/2、1/3、2、3次方,计算器中均有专门按键.〔3〕内移距p——为垂线长与圆曲线半径R之差.计算器输入：l02÷24÷R=2.曲线要素〔1〕切线长：计算器输入：<R+p>×tan<α÷2>+m=注意：偏角〔转角〕α,不论右偏还是左偏,其数值均取正值.公式中,如果右偏、左偏有影响,会通过正负系数ξ考虑.〔2〕曲线长：计算器输入：R×α×π÷180°+l0=〔3〕外矢距：计算器输入：<R+p>÷cos<α÷2>-R=〔4〕切曲差：计算器输入：2×T-L=3.曲线主点里程〔1〕〔2〕〔3〕〔4〕〔5〕注意：里程直接以米为单位写数值,写成DK***+***.****的形式.例如：起点里程为DK497+600.000,计算过程、结果均写作497600.000.所有结果均保留到小数点后三位,角度保留到计算器显示位数.4.坐标计算〔弦长弦切角法〕〔1〕根据已知点ZD、JD的坐标,作出这两个已知点的相对位置草图. 〔2〕第一条切线〔ZD-JD〕的坐标方位角：〔此知识点再讲〕计算器输入：tan-1<<Y JD-Y ZD>÷<X JD-X ZD>>=〔3〕计算ZH坐标：〔4〕计算缓和曲线上待求点i的坐标〔中线桩1、HY〕——直接使用弦长公式待求点i到ZH间曲线长：待求点i的放样直角坐标：计算器输入：〔5〕计算步骤先分别计算l1、l H中线桩1：HY：再输入X1公式,求X1得后,按计算器向左键"⊲〞,修改X1公式为Y1公式,依次求得Y1、Y HY、X HY.〔6〕计算圆曲线上待求点j的坐标〔中线桩2、QZ〕待求点j到HY间曲线长：待求点j的放样直角坐标：计算器输入：〔7〕计算步骤先分别计算l2、l Q中线桩2：QZ：再输入X2公式,求X2得后,按计算器向左键"⊲〞,修改X2公式为Y2公式,依次求得Y2、Y QZ、X QZ.注意：①arctan<*>,计算器中应输入tan-1<*>；先按SHIFT键,后按tan 键,即可调用.③α为偏角〔转角〕,不论右偏还是左偏,其数值均取正值.④ξ为曲线右左偏影响系数,右偏时,取1；左偏时,取-1.5.简明计算公式〔1〕缓和曲线切线角：〔2〕切垂距：〔3〕内移距：〔4〕切线长：〔5〕曲线长：〔6〕外矢距：〔7〕切曲差：〔8〕〔9〕〔10〕〔11〕〔12〕〔13〕第一条切线〔ZD-JD〕的坐标方位角：〔14、15〕计算ZH坐标：〔16-18〕计算缓和曲线上待求点i的坐标〔中线桩1、HY〕——直接使用弦长公式待求点i到ZH间曲线长：待求点i的放样直角坐标：〔19-21〕计算圆曲线上待求点j的坐标〔中线桩2、QZ〕待求点j到HY间曲线长：待求点j的放样直角坐标：第四部分：自己做练习根据例题的讲解,把竞赛的题目算完.。

第三节 缓和段一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间，由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。

1．缓和曲线的作用 1）便于驾驶员操纵方向盘2）乘客的舒适与稳定，减小离心力变化3）满足超高、加宽缓和段的过渡，利于平稳行车 4）与圆曲线配合得当，增加线形美观 2．缓和曲线的性质为简便可作两个假定：一是汽车作匀速行驶；二是驾驶员操作方向盘作匀角速转动，即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。

S=A 2/ρ（A ：与汽车有关的参数）ρ=C/s C=A 2由上式可以看出，汽车行驶轨迹半径随其行驶距离递减，即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比，此方程即回旋线方程。

3．回旋线基本方程即用回旋线作为缓和曲线的数学模型。

令：ρ=R ，l h =s 则 l h =A 2/R4．缓和曲线最小长度缓和曲线越长，其缓和效果就越好；但太长的缓和曲线也是没有必要的，因此这会给测设和施工带来不便。

缓和曲线的最小长度应按发挥其作用的要求来确定：1）根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性，就需控制离心力的变化率。

a 1=0,a 2=v 2/ρ,a s =Δa/t ≤0.6 RVl h 3035.0≥2）依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s) 2.16.3V t V vt l h ===3）根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡（即超高渐变率）是指在缓和曲线上设置超高缓和段后，因路基外侧由双向横坡逐渐变成单向超高横坡，所产生的附加纵坡。

ph l c h ≥4）从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间，视觉效果好。

《公路工程技术标准》规定：按行车速度来求缓和曲线最小长度，同时考虑行车时间和附加纵坡的要求。

5．直角坐标及要素计算 1）回旋线切线角（1）缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。