复习:第三章轴向拉伸和压缩
- 格式:ppt
- 大小:933.50 KB
- 文档页数:14



轴向拉伸与压缩的变形概念轴向拉伸与压缩是材料在受到外力作用下发生的一种变形形式。
这两种变形形式本质上都是由于材料内部的原子或分子受到外力的影响而改变了其平衡位置从而引起的。
轴向拉伸与压缩的变形概念可以通过弹簧的拉伸与压缩来加以理解。
首先我们来看轴向拉伸的变形。
当作用在弹簧两端的力朝相反方向拉伸时,弹簧会发生轴向拉伸的变形。
这是因为受到拉力的作用,弹簧内部原子或分子之间的间距增大,原本处于平衡位置的原子或分子会发生位移,使得整个弹簧长度增加。
这种拉力作用下的变形被称为轴向拉伸变形。
接下来我们来看轴向压缩的变形。
当作用在弹簧两端的力朝相同方向压缩时,弹簧会发生轴向压缩的变形。
这是因为受到压力的作用,弹簧内部原子或分子之间的间距减小,原本处于平衡位置的原子或分子会发生位移,使得整个弹簧长度减小。
这种压力作用下的变形被称为轴向压缩变形。
轴向拉伸与压缩的变形概念实际上可以通过杨氏模量来更加详细地描述。
杨氏模量是一个材料的机械特性参数,它描述了材料在轴向拉伸和压缩变形时的抵抗能力。
杨氏模量越大,材料的抵抗能力越强,抗拉强度也就越大。
相反地,杨氏模量越小,材料的抗拉强度越低。
在材料实际应用中,轴向拉伸与压缩的变形是非常常见的。
比如在建筑、桥梁、汽车、飞机等工程领域中,钢材往往被用于受力构件中,它能够在受到拉力或压力时保持较好的稳定性。
而在金属加工、塑料成型等制造领域中,轴向拉伸与压缩的变形则常常是一种设计和生产工艺。
例如在金属加工中,通过轴向拉伸可以制造出细丝,而通过轴向压缩则可以制造出坯料。
总结起来,轴向拉伸与压缩是材料在受到外力作用下发生的一种变形形式。
轴向拉伸是指材料的长度增加,原子或分子之间的间距变大;轴向压缩是指材料的长度减小,原子或分子之间的间距变小。
这两种变形形式与杨氏模量密切相关,它描述了材料在受力时的抵抗能力。
在工程和制造领域中,轴向拉伸与压缩的变形是非常常见的,它们对于材料的选择、设计和生产工艺具有重要意义。


第三章 轴向拉伸和压缩一、选择题( )1、轴向拉伸或压缩时,直杆横截面上的内力称为轴力,表示为_______A.N FB. FSC.Q F D.jy F( )2、截面上的内力大小,________。
A.与截面的尺寸和形状无关B.与截面的尺寸有关,但与截面的形状无关C.与截面的尺寸无关,但与截面的形状有关D.与截面的尺寸和形状都有关( )3、等截面直杆在两个外力的作用下发生轴向压缩变形时,这对外力所具备的特点一 定是等值、_______。
A.反向、共线B.反向,过截面形心C.方向相对,作用线与杆轴线重合D.方向相对,沿同一直线作用( )4、一阶梯形杆件受拉力P的作用,其截面1-1,2-2,3-3上的内力分别为N1,N2 和N3,三者的关系为_______。
A.N1≠N2 N2≠N3B.N1=N2 N2=N3C.N1=N2 N2>N3D.N1=N2 N2<N3( )5、图示阶梯形杆,CD 段为铝,横截面面积为A ;BC 和DE 段为钢,横截面面积均为 2A 。
设1-1、2-2、3-3截面上的正应力分别为σ1、σ2、σ3,则其大小次序为_______。
A.σ1>σ2>σ3B.σ2>σ3>σ1C.σ3>σ1>σ2D.σ2>σ1>σ3( )6、轴向拉伸杆,正应力最大的截面和剪应力最大的截面_______。
A.分别是横截面、450斜截面B.都是横截面C.分别是450斜截面、横截面D.都是450斜截面( )7、由变形公式Δl =Pl/EA 即E =Pl/A Δl 可知,弹性模量_______。
A.与载荷、杆长、横截面面积无关B.与载荷成正比C.与杆长成正比D.与横截面面积成正比( )8、在下列说法,_______是正确的。
A 内力随外力增大而增大B 内力与外力无关C 内力随外力增大而减小D 内力沿杆轴是不变( )9、在轴向拉伸或压缩杆件上正应力为零的截面是_______。
A.横截面B.与轴线成一定交角的斜截面C.沿轴线的截面D.不存在的( )10、一圆杆受拉,在其弹性变形范围内,将直径增加一倍,则杆的相对变形将变为原 来的_______倍。


材料力学(一)轴向拉伸与压缩【内容提要】材料力学主要研究构件在外力作用下的变形、受力与破坏、失效的规律。
为设计既安全可靠又经济合理的构件,提供有关强度、刚度与稳定性分析的基本理论与方法。
【重点、难点】重点考察基本概念,掌握截面法求轴力、作轴力图的方法,截面上应力的计算。
【内容讲解】一、基本概念强度—-构件在外力作用下,抵抗破坏的能力,以保证在规定的使用条件下,不会发生意外的断裂或显著塑性变形.刚度-—构件在外力作用下,抵抗变形的能力,以保证在规定的使用条件下不会产生过分的变形。
稳定性--构件在外力作用下,保持原有平衡形式的能力,以保证在规定的使用条件下,不会产生失稳现象。
杆件——一个方向的尺寸远大于其它两个方向的尺寸的构件,称为杆件或简称杆。
根据轴线与横截面的特征,杆件可分为直杆与曲杆,等截面杆与变截面杆。
二、材料力学的基本假设工程实际中的构件所用的材料多种多样,为便于理论分析,根据它们的主要性质对其作如下假设。
(一)连续性假设-—假设在构件所占有的空间内均毫无空隙地充满了物质,即认为是密实的。
这样,构件内的一些几何量,力学量(如应力、位移)均可用坐标的连续函数表示,并可采用无限小的数学分析方法。
(二)均匀性假设——很设材料的力学性能与其在构件中的位置无关。
按此假设通过试样所测得的材料性能,可用于构件内的任何部位(包括单元体).(三)各向同性假设——沿各个方向均具有相同力学性能。
具有该性质的材料,称为各向同性材料。
综上所述,在材料力学中,一般将实际材料构件,看作是连续、均匀和各向同性的可变形固体。
三、外力内力与截面法(一)外力对于所研究的对象来说,其它构件和物体作用于其上的力均为外力,例如载荷与约束力.外力可分为:表面力与体积力;分布力与集中力;静载荷与动载荷等.当构件(杆件)承受一般载荷作用时,可将载荷向三个坐标平面(三个平面均通过杆的轴线,其中两个平面为形心主惯性平面)内分解,使之变为两个平面载荷和一个扭转力偶作用情况.在小变形的情况下,三个坐标平面内的力互相独立,即一个坐标平面的载荷只引起这一坐标平面内的内力分量,而不会引起另一坐标平面内的内力分量。


材料力学 - 轴向拉伸和压缩材料力学是研究材料性质和行为的学科,包括弹性、塑性、疲劳、断裂等方面。
在材料力学中,轴向拉伸和压缩是重要的力学测试方法。
轴向拉伸测试轴向拉伸测试是材料测试中最常用的测试方法之一。
该测试方法涉及将试验样品拉伸至破裂点,并测量在拉伸过程中的应力和应变。
在这种测试中,试验样品的截面积比长度更重要,因为应力是由试样的横截面积决定的。
实验过程首先,通过切割样品制备试样。
样品应该是长条状,尺寸应该足够大,能够容纳拉伸机的夹具和测量设备。
然后将样品置于拉伸机上,将试样夹具固定在机器的上部,并将另一个夹具固定在机器的下部。
然后将机器调整到适当的测试条件,比如设置测试速度、卸载条件等。
开始拉伸后,由于拉伸过程会导致不均匀应变,需要使用应变计进行应变测量。
最后,测试结果应该包括应力 - 应变曲线和破坏点。
结果解释轴向拉伸测试的结果由两种性质构成:杨氏模量和屈服强度。
杨氏模量衡量材料的弹性变形特性,而屈服强度则衡量材料开始塑性变形的能力。
在拉伸试验中,将出现线性区域,在该区域,样品的杨氏模量可由应力-应变曲线的斜率计算。
当样品的应变超过线性区域后,就会进入塑性区域,此时材料会表现出不可逆的形变特性。
轴向压缩测试轴向压缩测试是一种用于测量材料在压缩负载下的应变和应力的测试方法。
在这种测试中,材料试件放置在压力夹具之间,并受到垂直于试件轴向的载荷。
压缩测试与轴向拉伸测试非常相似,但它们的结果不同。
由于材料的差异,它们所能承受的压缩力和拉伸力也会存在一定的不同。
实验过程样品制备和夹具的选择与轴向拉伸测试类似,但是在拉伸试验机与压缩机之间存在差异。
进行轴向压缩测试时,需要将夹具安装在垂直于轴向的方向上,并将试件放置在夹具内。
与轴向拉伸测试相同,需要记录测试过程中的应变和应力变化。
结果解释与轴向拉伸测试一样,轴向压缩测试的结果也由杨氏模量和屈服强度构成。
杨氏模量是指在材料的弹性变形区域中,材料的应力与应变的比例系数。

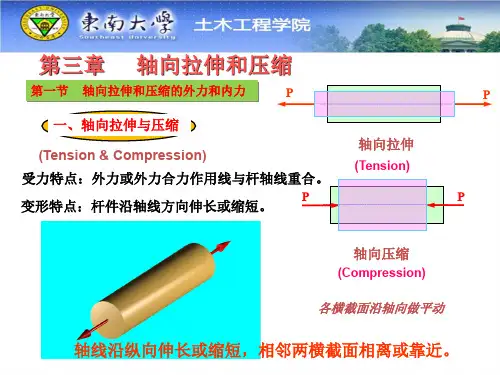
轴向拉伸与压缩的名词解释引言:轴向拉伸与压缩是物理学领域中常见的概念,用于描述物体在力的作用下的变形情况。
本文将对轴向拉伸与压缩进行详细的解释与探讨。
一、轴向拉伸轴向拉伸是指物体在受到拉力作用下沿着其长度方向发生的变形现象。
当外力作用于物体的两端,并朝外拉伸时,物体会在轴向上发生拉伸。
拉伸的大小可以通过物体的伸长率来衡量,伸长率定义为单位长度的伸长与初始长度之比。
轴向拉伸现象广泛应用于工程领域,例如建筑中的钢筋,拉伸试验中的拉力传感器等。
钢筋在混凝土中起到增强材料的作用,能够抵抗建筑物的拉力。
而拉力传感器则是一种能够测量外力大小的传感器,利用了材料的拉伸特性。
二、轴向压缩轴向压缩是指物体在受到压力作用下沿着其长度方向发生的变形现象。
当外力作用于物体的两端,并朝内压缩时,物体会在轴向上发生压缩。
压缩的大小可以通过物体的压缩率来衡量,压缩率定义为单位长度的压缩与初始长度之比。
轴向压缩现象同样广泛应用于工程领域。
例如,桥梁中的墩柱、压缩试验中的压力传感器等。
墩柱是承受桥梁重力和交通荷载的重要结构部件,压缩试验中的压力传感器则是能够测量外力大小的传感器,利用了材料的压缩特性。
三、轴向拉伸与压缩的应用轴向拉伸与压缩的应用十分丰富,不仅在工程领域中有广泛应用,在其他领域中也有其独特的应用价值。
1. 材料科学:轴向拉伸与压缩是材料性能研究的重要手段。
通过对材料在拉伸和压缩条件下的变形进行测试,可以获得材料的各种力学性能参数,例如抗拉强度、抗压强度等。
这对材料的设计和应用具有重要的指导意义。
2. 生物医学:轴向拉伸与压缩在生物医学研究中具有重要的作用。
例如,在骨骼生物力学研究中,可以通过对骨骼的拉伸和压缩测试,了解骨骼力学特性并分析疾病的发生机制。
3. 电子工程:轴向拉伸与压缩的特性也可以应用于电子工程领域。
例如,电子产品中常使用弹性材料来保护内部电路。
这些材料可以在外力作用下发生轴向拉伸或压缩,起到减缓冲击力的作用。