ABAQUS_材料本构模型与编程

基于Abaqus子程序的高分子材料本构关系实现作者：汪品红来源：《计算机辅助工程》2013年第05期摘要：对于高分子材料的仿真，业界一般使用经典的弹塑性本构模型来描述其应力应变关系，但其真实的应力应变关系与经典的弹塑性本构模型存在一定差异，从而导致仿真与实际测试之间的差异.Abaqus提供UMAT/VUMAT子程序接口，让用户可以自己构建新的材料本构模型.通过撰写新的材料本构子程序实现高分子材料应力应变关系在仿真中的准确描述，减少仿真与测试之间的差异.同时，在卸载段可以通过卸载标志符的选择定义不同的卸载路径，方便用户使用.关键词：高分子材料；本构关系； Abaqus； UMAT； VUMAT中图分类号： TB324； TB115.1文献标志码： B引言高分子材料在日常生活中有着广泛的应用，因此其不可避免地出现在仿真分析中.当前没有一种商业软件具有适合高分子材料的材料本构模型.Abaqus是一款优秀的商业软件，其提供的子程序接口UMAT/VUMAT允许用户根据使用需求自定义材料本构.[1]使用该方法，可有效解决在仿真中由于材料本构不适用而导致的仿真与实际测试差异过大的问题.1高分子材料本构一般描述方法业界通常使用弹塑性本构定义高分子材料的材料属性.屈服强度一般取材料曲线上第一个峰值点.弹性模量的取法有2种不同的方式：对于应力应变关系曲线有明显直线段的，以第一段直线的斜率作为材料的弹性模量（切线法）；对于曲线没有明显直线段的材料，则使用原点与屈服点连成的直线的斜率作为弹性模量（割线法）.2种方式与真实应力应变曲线的比较见图1.图 1高分子材料测试材料曲线与仿真曲线比较由图1可知，无论使用何种方式，仿真使用的应力应变曲线都与实际材料的应力应变曲线有较大差异.将切线法获得材料数据代入到手机电池盖三点弯曲中进行仿真，见图2，其仿真与测试力位移曲线在最高点的差异约为23%，见图3.对于手机等一些电子类产品，高分子材料的仿真非常重要.在跌落或弯折测试中，高分子材料的应力应变关系与弹塑性本构的差异造成仿真预测不准确，必须定义正确的高分子材料本构.2Abaqus VUMAT子程序Abaqus提供丰富的材料本构模型库，能够满足绝大多数仿真材料模型的需要；同时，还提供UMAT/VUMAT子程序接口，让用户可以用FORTRAN语言编程，自己定义需要的材料本构模型，对Abaqus材料库中没有包含的材料进行计算.几乎可以把用户材料属性赋予Abaqus 中的任何单元，其中UMAT用在隐式仿真计算中，VUMAT用在显式仿真计算中.由于隐式计算与显式计算的差别，导致UMAT与VUMAT也有一定的差异，但是经过简单的改写即可完成它们之间的转换.本文使用准静态仿真分析方法，属于显式求解，所以只介绍VUMAT.3高分子材料VUMAT本构介绍由图1可知，高分子材料的本构与弹塑性本构最大的差异在于弹性段是直线还是曲线.弹性段的路径也直接影响到卸载的路径.因此，对高分子材料本构的定义关键在于非线性弹性段的实现，即要根据当前的应力值实时获取下一增量步所用的弹性模量值.程序整体流程见图4.图 4程序整体流程3.1弹性段多段线性的实现在弹性段，程序根据弹性模量和泊松比计算应力增量.由于弹性段为非线性，需要根据应力或应变更新用于计算的弹性模量值，直至达到屈服点，因此需要在输入文件中输入材料真实应力应变曲线，通过查表计算的函数，根据当前应力σ所在的位置，计算当前的弹性模量.应力应变曲线输入时，输入格式为：用查表的方法，直到σn3.2卸载路径的选择屈服发生后，需要选择弹性模量参与相关计算，有2个作用：一是用来计算屈服后加载段的应力试探值（不对该增量步真实应力产生影响，只起对比判断的作用）；二是用来作为屈服后卸载的路径（为实现不同卸载路径，在程序中设置一个flag位，其值由用户自己输入），用户可以根据实际的需要选择卸载的路径.如图4中，共设置3种卸载路径：沿切线卸载、沿割线卸载以及沿曲线卸载等.用户也可以根据需要增加其他的卸载方式.4子程序的验证为验证子程序是否能实现设计的功能，取一个1/8的网格模型进行单轴拉伸仿真，单元类型为C3D8R.输出其应力应变曲线，与材料真实应力应变曲线比较，见图5.图 5使用VUMAT后加载应力应变曲线与材料曲线对比使用VUMAT后，加载的应力应变曲线与材料测试得到的真实应力应变曲线完全重合，说明VUMAT可以完全反映材料在加载过程中的力学行为.在卸载过程中，分别实现沿弹性段的切线、割线以及曲线卸载.为进一步验证，将VUMAT用于图2所示的手机电池盖三点弯模型中进行仿真与试验对比.在使用弹塑性本构模型时，仿真与测试力位移曲线的最大差异约为23%，而引入使用VUMAT 编写的高分子材料本构后，其仿真与测试的差异减少到4.5%，见图6.从实际项目的验证结果看，使用VUMAT后电池盖测试的力位移曲线与仿真的力位移曲线基本重合，仿真与测试的差异也明显减小.将该本构应用于其他高分子材料和实际案例，其仿真精度均明显改善，也说明该子程序在实际工程中的适用性.图 6使用VUMAT后电池盖力位移曲线对比5结束语使用VUMAT子程序后，高分子材料在加载段的力学特性与测试的真实应力应变曲线一致，同时将其应用在工程实际问题上，也与测试曲线基本一致，验证该程序的适用性.由于高分子材料的卸载特性较为复杂，还需进一步研究，所以程序只给出3种方式供用户按照实际需求进行选择.参考文献：[1]庄茁，张帆，岑松，等. 基于Abaqus的有限元分析和应用[M]. 北京：清华大学出版社， 2009： 509512.（编辑武晓英）。

abaqus操作流程Abaqus操作流程Abaqus是一款强大的有限元分析软件，广泛应用于工程、科学和研究领域。

本文将介绍Abaqus的操作流程，包括软件安装、模型建立、材料定义、边界条件设置、求解和后处理等步骤。

一、软件安装需要从官方网站下载Abaqus软件，并按照安装向导进行安装。

安装完成后，需要激活软件，通常需要输入许可证文件或者许可证服务器地址。

如果是学术版或者试用版，可以直接使用。

二、模型建立在Abaqus中，可以通过几何建模、导入CAD模型或者手动输入节点和单元来建立模型。

几何建模是最常用的方法，可以使用Abaqus CAE中的几何建模工具，例如绘制线、面、体等基本几何体，然后进行布尔运算、切割、倒角等操作，最终生成复杂的几何模型。

导入CAD模型需要将CAD文件转换为Abaqus支持的格式，例如STEP、IGES、ACIS等。

手动输入节点和单元需要了解节点和单元的类型、编号、坐标等信息，比较繁琐，不建议使用。

三、材料定义在Abaqus中，需要定义材料的力学性质，例如弹性模量、泊松比、屈服强度等。

可以选择预定义的材料模型，例如线弹性、非线性弹性、塑性等，也可以自定义材料模型。

自定义材料模型需要了解材料的本构关系，例如应力-应变曲线，可以通过实验或者理论计算得到。

四、边界条件设置在Abaqus中，需要设置边界条件，包括约束和载荷。

约束是指模型的某些部分不能移动或者旋转，例如固定支座、铰链等。

载荷是指模型受到的外部力或者压力，例如重力、风荷载、温度载荷等。

可以选择预定义的边界条件，例如固定支座、均布载荷等，也可以自定义边界条件。

自定义边界条件需要了解模型的物理特性和边界条件的作用方式。

五、求解在Abaqus中，需要进行求解，即求解模型的应力、应变、位移等物理量。

可以选择不同的求解器，例如标准求解器、隐式求解器、动态求解器等，也可以选择不同的求解方法，例如直接法、迭代法等。

求解过程中需要注意模型的收敛性和稳定性，如果模型不收敛或者不稳定，需要调整求解器和求解参数。

一、概述1.1 abaqus是什么Abaqus是一款用于进行有限元分析的软件，它可以模拟各种工程材料在不同应力应变条件下的力学性能，为产品设计和工程分析提供了重要的支持。

1.2 应力应变曲线本构应力应变曲线本构是描述材料在不同应变条件下的应力应变关系的数学模型，用于分析材料在不同加载条件下的强度和变形性能。

在abaqus中，输入应力应变曲线本构是十分重要的一步，它决定了模拟分析的准确性和可靠性。

二、 abaous输入应力应变曲线本构的方法2.1 材料的本构模型在abaqus中，材料的本构模型是用于描述材料在应力应变条件下的力学性能的数学模型。

常见的本构模型包括线性弹性本构、非线性弹性本构和塑性本构等。

对于不同的材料和工程条件，需要选择合适的本构模型来准确模拟材料的力学性能。

2.2 输入应力应变曲线在abaqus中，输入应力应变曲线本构的方法主要包括以下步骤：（1）确定材料的本构模型，选择合适的本构模型对材料的应力应变曲线进行描述。

（2）测定材料的应力应变曲线，通过实验或者理论计算等方法获取材料在不同应变条件下的应力应变关系数据。

（3）将实验或理论得到的应力应变数据输入到abaqus软件中，通过合适的参数设置和插值方法，建立起材料的应力应变曲线本构模型。

2.3 应力应变曲线本构的应用输入应力应变曲线本构后，abaqus可以进行模拟分析，对材料在不同工况下的力学性能进行计算和预测。

利用输入的应力应变曲线本构，abaqus可以准确模拟材料的强度、刚度、变形性能等，并为工程设计和分析提供重要的参考。

三、输入应力应变曲线本构的注意事项3.1 数据的准确性输入应力应变曲线本构前，需要确保所使用的应力应变数据具有较高的准确性和可靠性。

对于实验数据，需要进行充分的测试和验证；对于理论计算数据，需要保证所使用的材料模型和参数的准确性。

3.2 本构模型的选择在进行输入应力应变曲线本构时，需要根据材料的力学性能和所处的工程条件，选择合适的本构模型。

abaqus 模拟材料力学扭转试验方法Abaqus模拟材料力学扭转试验方法引言：材料力学扭转试验是评估材料在受到扭转载荷下的变形和破坏特性的一种重要方法。

在工程实践中，了解材料的扭转性能对于设计和分析各种结构和部件具有重要意义。

本文将介绍如何使用ABAQUS软件进行材料力学扭转试验的模拟，以便更好地理解材料的扭转行为。

一、试验背景材料力学扭转试验是通过施加一个扭转载荷来研究材料的变形和破坏行为。

在试验中，材料样本通常采用圆柱形状，通过扭转机构施加一个扭转力矩，测量样本的扭转角度和扭转力矩，从而得到材料的扭转应力和扭转应变。

二、建立模型1. 创建几何模型：根据实际材料样本的几何形状，使用ABAQUS提供的几何建模工具创建一个圆柱形样本模型。

2. 定义材料属性：根据实际材料的力学性能指标，定义材料的弹性模量、泊松比和屈服强度等参数。

3. 网格划分：对样本进行网格划分，确保网格密度适中，以便准确模拟材料的变形和破坏行为。

三、施加边界条件在模拟中，需要施加适当的边界条件来模拟真实试验中的约束和加载条件。

根据实际情况，可以采用固定边界条件约束样本的底部，并施加一个扭转力矩在样本的顶部。

四、定义材料本构模型ABAQUS提供了多种本构模型来描述材料的力学行为。

根据实际材料的性质和试验要求，选择适当的本构模型，如线性弹性模型、非线性弹性模型或塑性本构模型。

五、指定加载条件根据试验要求，指定加载条件，即施加扭转力矩的大小和加载速率。

可以根据实际试验数据或已有的材料力学性能曲线来指定加载条件。

六、运行模拟并分析结果在模型设置完成后，运行ABAQUS模拟，并通过后处理功能来分析结果。

可以得到材料样本的扭转角度、扭转力矩和应力应变分布等信息，以评估材料的扭转性能。

七、结果验证与优化将模拟结果与实验数据进行对比，并进行结果验证与优化。

如果模拟结果与实验结果吻合较好，则可以认为模拟是准确可靠的。

如果存在差异，需要对模型和参数进行调整，以更好地模拟材料的扭转行为。

ABAQUS显式分析梁单元的混凝土、钢筋本构模型共3篇ABAQUS显式分析梁单元的混凝土、钢筋本构模型1在ABAQUS中，梁单元是一种经常用于模拟混凝土和钢筋梁的元素。

它使用线性或非线性混凝土本构模型和钢筋本构模型来描述材料的行为，并考虑梁单元在三个方向上的应力和应变。

混凝土本构模型:ABAQUS提供了多个混凝土本构模型，它们可以用于描述混凝土的本构行为。

其中一个常用的模型是Mander本构模型，它考虑了混凝土的三个不同阶段的行为：1. 压缩阶段: 混凝土在受到压缩时会逐渐变硬，所以Mander模型使用一个非线性的应力-应变关系来描述混凝土的压缩行为。

该模型使用三个参数来描述混凝土在不同应变范围内的硬化行为。

2. 弯曲-拉伸阶段: 当混凝土受到弯曲或拉伸时，会发生一些微小的裂缝，导致其变得更容易受到破坏。

因此，Mander模型采用一个渐进应力-应变关系来描述混凝土的弯曲和拉伸行为。

该模型也使用三个参数来描述不同应变范围内的弯曲和拉伸行为。

3. 破坏阶段: 当混凝土受到极大应力时，会发生破坏。

为了模拟破坏行为，Mander模型使用两个参数来描述混凝土的弹性模量和极限应变。

当混凝土受到超过极限应变的应变时，该模型将输出一个非常大的应力值，这意味着梁单元已经破坏。

钢筋本构模型:ABAQUS也提供了多个钢筋本构模型。

其中一个常用的模型是多屈服弹塑性模型，它考虑了钢筋的应力-应变关系的多个拐点：1. 弹性阶段: 在应力小于屈服强度时，钢筋的行为是弹性的。

因此，多屈服弹塑性模型使用一个线性应力-应变关系来描述弹性阶段的行为。

2. 屈服阶段: 当钢筋的应力达到屈服强度时，它的行为将开始变得非线性。

因此，多屈服弹塑性模型使用一个拐点来描述屈服后的应力-应变关系。

该模型使用一组参数来描述每个拐点的应力和应变差。

3. 再次弹性阶段: 当钢筋的应变超过屈服点后，它的应变-应力关系将再次变得线性。

多屈服弹塑性模型也考虑了这个阶段的行为。

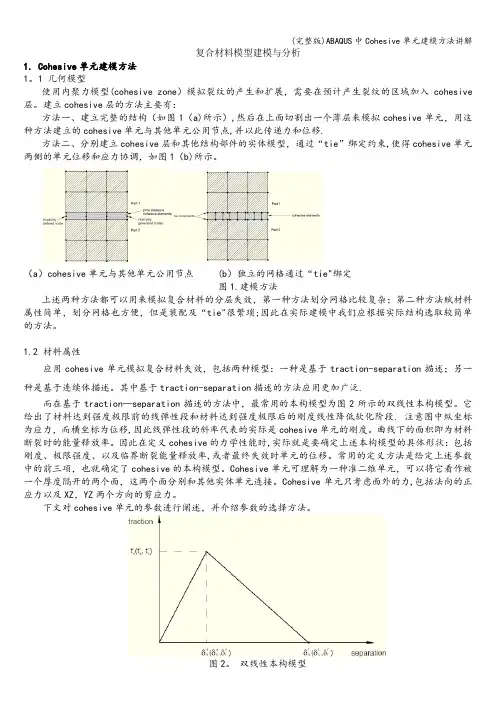
复合材料模型建模与分析1. Cohesive单元建模方法1。

1 几何模型使用内聚力模型(cohesive zone）模拟裂纹的产生和扩展，需要在预计产生裂纹的区域加入cohesive 层。

建立cohesive层的方法主要有：方法一、建立完整的结构（如图1（a)所示）,然后在上面切割出一个薄层来模拟cohesive单元，用这种方法建立的cohesive单元与其他单元公用节点,并以此传递力和位移.方法二、分别建立cohesive层和其他结构部件的实体模型，通过“tie”绑定约束,使得cohesive单元两侧的单元位移和应力协调，如图1（b)所示。

（a）cohesive单元与其他单元公用节点 (b）独立的网格通过“tie"绑定图1.建模方法上述两种方法都可以用来模拟复合材料的分层失效，第一种方法划分网格比较复杂；第二种方法赋材料属性简单，划分网格也方便，但是装配及“tie"很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。

1.2 材料属性应用cohesive单元模拟复合材料失效，包括两种模型：一种是基于traction-separation描述；另一种是基于连续体描述。

其中基于traction-separation描述的方法应用更加广泛.而在基于traction—separation描述的方法中，最常用的本构模型为图2所示的双线性本构模型。

它给出了材料达到强度极限前的线弹性段和材料达到强度极限后的刚度线性降低软化阶段. 注意图中纵坐标为应力，而横坐标为位移,因此线弹性段的斜率代表的实际是cohesive单元的刚度。

曲线下的面积即为材料断裂时的能量释放率。

因此在定义cohesive的力学性能时,实际就是要确定上述本构模型的具体形状：包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。

常用的定义方法是给定上述参数中的前三项，也就确定了cohesive的本构模型。

abaqus中johnson-cook本构模型理解-回复什么是ABAQUS？ABAQUS是一种商业有限元分析软件，可用于模拟和分析复杂的结构、材料和物理过程。

它提供了广泛的分析功能和完整的建模工具，以帮助工程师和研究人员解决各种问题。

Johnson-Cook本构模型是什么？本构模型是材料力学中用于描述物质的应变-应力关系的数学模型。

Johnson-Cook本构模型是一种经验本构模型，适用于金属材料在高应变速率和高温条件下的塑性行为。

它是根据大量实验数据拟合而得，能够准确地预测材料在复杂工况下的力学行为。

Johnson-Cook本构模型的基本形式为：σ= (A + Bε^n)(1 + C(ln(ε_p))^m)(1 - (T - T_0)^p)其中，σ是应力，ε是总应变，ε_p是等效塑性应变，T是温度，T_0是参考温度。

A、B、C、n、m和p是拟合参数，可以根据材料的实验数据进行确定。

Johnson-Cook本构模型的理解和应用：1. 适用范围和限制Johnson-Cook本构模型适用于金属材料在高应变速率和高温条件下的塑性行为。

它广泛应用于冲击、爆炸、高速碰撞等动力学加载条件下的模拟分析。

然而，它也有一些局限性，如适用于单一相材料，对复杂的孪晶结构和多相材料的预测能力有限。

2. 模型参数的确定Johnson-Cook本构模型的参数包括A、B、C、n、m和p，这些参数可以通过材料的实验数据和拟合方法进行确定。

A和B参数分别表示材料的强度和硬化特性，C参数表示材料的温度敏感性，n参数表示材料的硬化指数，m参数表示材料的温度敏感指数，p参数表示材料的温度衰减指数。

通过对实验数据的统计分析和拟合，可以得到这些参数的值。

3. 模型的应用Johnson-Cook本构模型可以在ABAQUS软件中使用，用于模拟和分析金属材料在高应变速率和高温条件下的力学行为。

通过将该模型与适当的加载条件和边界条件结合使用，可以准确地预测材料在复杂工况下的力学响应。

前言有限元法是工程中广泛使用的一种数值计算方法。

它是力学、计算方法和计算机技术相结合的产物。

在工程应用中，有限元法比其它数值分析方法更流行的一个重要原因在于：相对与其它数值分析方法，有限元法对边界的模拟更灵活，近似程度更高。

所以，伴随着有限元理论以及计算机技术的发展，大有限元软件的应用证变得越来越普及。

ABAQUS软件一直以非线性有限元分析软件而闻名，这也是它和ANSYS,Nastran等软件的区别所在。

非线性有限元分析的用处越来越大，因为在所用材料非常复杂很多情况下，用线性分析来近似已不再有效。

比方说，一个复合材料就不能用传统的线性分析软件包进行分析。

任何与时间有关联，有较大位移量的情况都不能用线性分析法来处理。

多年前，虽然非线性分析能更适合、更准确的处理问题，但是由于当时计算设备的能力不够强大、非线性分析软件包线性分析功能不够健全，所以通常采用线性处理的方法。

这种情况已经得到了极大的改善，计算设备的能力变得更加强大、类似ABAQUS这样的产品功能日臻完善，应用日益广泛。

非线性有限元分析在各个制造行业得到了广泛应用，有不少大型用户。

航空航天业一直是非线性有限元分析的大客户，一个重要原因是大量使用复合材料。

新一代波音 787客机将全部采用复合材料。

只有像 ABAQUS这样的软件，才能分析包括多个子系统的产品耐久性能。

在汽车业，用线性有限元分析来做四轮耐久性分析不可能得到足够准确的结果。

分析汽车的整体和各个子系统的性能要求（如悬挂系统等）需要进行非线性分析。

在土木工程业， ABAQUS能处理包括混凝土静动力开裂分析以及沥青混凝土方面的静动力分析，还能处理高度复杂非线性材料的损伤和断裂问题，这对于大型桥梁结构，高层建筑的结构分析非常有效。

瞬态、大变形、高级材料的碰撞问题必须用非线性有限元分析来计算。

线性分析在这种情况下是不适用的。

以往有一些专门的软件来分析碰撞问题，但现在ABAQUS在通用有限元软件包就能解决这些问题。

基于abaqus的木材本构关系数值模拟方法1.引言1.1 概述概述部分的内容示例：在工程领域中，对木材的力学性能和行为的研究一直存在着广泛的关注。

木材作为一种常见的工程材料，其强度、刚度和耐久性对于工程结构的设计和安全具有重要的影响。

研究木材本构关系是了解木材力学行为及其材料特性的基础，对于优化木材结构的设计和评估具有重要意义。

随着计算机技术的进步和有限元分析方法的广泛应用，通过数值模拟方法来研究木材本构关系变得越来越普遍和有效。

其中，ABAQUS作为一款常用的有限元分析软件，具有强大的建模和分析能力，被广泛应用于各个领域的工程问题求解中。

基于ABAQUS的数值模拟方法可以通过建立木材的有限元模型，模拟木材受力过程中的变形、应力分布和破坏行为。

本文旨在介绍基于ABAQUS的数值模拟方法，用于研究木材的本构关系。

首先，将会概述木材本构关系的研究现状，包括已有的实验数据和模型。

然后，介绍基于ABAQUS的数值模拟方法，包括材料参数的输入、模型的建立和加载条件的设置。

通过数值模拟可以得到木材在各种力学载荷下的力学性能，进而分析其行为特性。

最后，通过结果分析，我们将对该数值模拟方法的有效性和实用性进行评价，并指出研究的局限性以及未来的发展方向。

本文的研究旨在提供一种基于ABAQUS的数值模拟方法，为工程师和研究人员提供一个有效的工具，用于理解和预测木材的力学行为和性能，以支持木材结构的合理设计和优化。

希望本文的内容能够对读者在木材本构关系的研究和应用方面提供一定的指导和参考。

文章结构部分的内容可以按照以下方式进行编写：本篇文章的结构如下：一、引言1.1 概述1.2 文章结构1.3 目的二、正文2.1 木材本构关系的研究现状2.2 基于abaqus的数值模拟方法三、结论3.1 结果分析3.2 研究的局限性和展望在引言部分，我们将对本文的研究背景、意义和目的进行介绍。

首先，我们会提出木材本构关系的研究现状，包括目前已有的研究成果以及存在的问题。

5083 铝合金是一种常用的可热处理强化的铝合金，其主要成分为铝（Al）、镁（Mg）、硅（Si）和少量铬（Cr）、锌（Zn）等元素。

在ABAQUS 中，我们可以使用Johnson-Cook 本构模型来描述5083 合金的材料行为。

Johnson-Cook 模型是一种热力学耦合的模型，可以描述材料在高温高应变率下的动态响应。

为了定义5083 合金在ABAQUS 中的本构参数，我们需要以下数据：
1. 弹性模量（E）：材料在弹性范围内的应力与应变之比。

2. 屈服强度（σ_y）：材料开始塑性变形的应力值。

3. 极限强度（σ_u）：材料在拉伸过程中的最大应力值。

4. 应变率敏感系数（β）：材料对应变率的敏感程度。

5. 热膨胀系数（α）：材料在温度变化时的线性膨胀率。

6. 比热容（c_p）：材料在恒定压力下的比热容。

7. 密度（ρ）：材料的密度。

8. 初始温度（T_0）：材料的初始温度。

9. 冷却速率（β）：材料在热处理过程中的冷却速率。

在ABAQUS 中，可以通过以下步骤定义5083 合金的本构参数：
1. 创建一个材料卡片，选择Johnson-Cook 本构模型。

2. 输入弹性模量、屈服强度、极限强度等基本参数。

3. 输入应变率敏感系数、热膨胀系数、比热容等耦合参数。

4. 输入密度、初始温度等热力学参数。

5. 根据实验数据，拟合Johnson-Cook 模型中的其他参数。

6. 完成本构参数的定义。

前言有限元法是工程中广泛使用的一种数值计算方法。

它是力学、计算方法和计算机技术相结合的产物。

在工程应用中，有限元法比其它数值分析方法更流行的一个重要原因在于：相对与其它数值分析方法，有限元法对边界的模拟更灵活，近似程度更高。

所以，伴随着有限元理论以及计算机技术的发展，大有限元软件的应用证变得越来越普及。

ABAQUS软件一直以非线性有限元分析软件而闻名，这也是它和ANSYS,Nastran等软件的区别所在。

非线性有限元分析的用处越来越大，因为在所用材料非常复杂很多情况下，用线性分析来近似已不再有效。

比方说，一个复合材料就不能用传统的线性分析软件包进行分析。

任何与时间有关联，有较大位移量的情况都不能用线性分析法来处理。

多年前，虽然非线性分析能更适合、更准确的处理问题，但是由于当时计算设备的能力不够强大、非线性分析软件包线性分析功能不够健全，所以通常采用线性处理的方法。

这种情况已经得到了极大的改善，计算设备的能力变得更加强大、类似ABAQUS这样的产品功能日臻完善，应用日益广泛。

非线性有限元分析在各个制造行业得到了广泛应用，有不少大型用户。

航空航天业一直是非线性有限元分析的大客户，一个重要原因是大量使用复合材料。

新一代波音 787客机将全部采用复合材料。

只有像 ABAQUS这样的软件，才能分析包括多个子系统的产品耐久性能。

在汽车业，用线性有限元分析来做四轮耐久性分析不可能得到足够准确的结果。

分析汽车的整体和各个子系统的性能要求（如悬挂系统等）需要进行非线性分析。

在土木工程业， ABAQUS能处理包括混凝土静动力开裂分析以及沥青混凝土方面的静动力分析，还能处理高度复杂非线性材料的损伤和断裂问题，这对于大型桥梁结构，高层建筑的结构分析非常有效。

瞬态、大变形、高级材料的碰撞问题必须用非线性有限元分析来计算。

线性分析在这种情况下是不适用的。

以往有一些专门的软件来分析碰撞问题，但现在ABAQUS在通用有限元软件包就能解决这些问题。

abaqus 钢拉伸断裂本构Abaqus钢拉伸断裂本构模型引言：钢材具有广泛应用于结构工程和制造领域的优异性能。

对于钢材的拉伸断裂性能的研究对于提高结构工程的安全性和可靠性具有重要意义。

本文将以Abaqus软件为工具，详细介绍钢材拉伸断裂本构模型的建立和分析方法。

一、拉伸断裂本构模型的基本原理拉伸断裂本构模型是用来描述材料受拉应力时产生断裂的模型。

在Abaqus中，常用的模型有线性弹性模型、虚伪贝努力模型和真实贝努力模型等。

这些模型基于材料力学、断裂力学及实验数据等理论基础，通过对应力应变关系的描述，可以模拟钢材在拉伸断裂过程中的力学行为。

二、Abaqus软件中钢材断裂本构模型的建立1. 定义材料属性：在Abaqus中，首先需要定义材料的力学特性。

对于钢材，可以通过实验数据获取材料的弹性模量、屈服强度、断裂强度等力学特性参数。

2. 选择本构模型：根据所选材料的特性，选择合适的本构模型。

常用的本构模型有线性弹性模型、虚伪贝努力模型和真实贝努力模型等，根据具体研究需求选择适用的模型。

3. 定义本构模型参数：根据所选本构模型，定义相应的本构模型参数。

不同的模型有不同的参数定义，根据实际需求确定参数取值。

4. 建立材料模型：在Abaqus中，通过使用材料模型定义命令，将材料的力学特性和本构模型参数输入软件中。

通过这一步骤，软件就能够了解钢材的力学特性和本构行为。

三、Abaqus软件中钢材断裂分析的步骤1. 几何建模：在Abaqus中，首先需要进行几何建模。

根据具体的分析需求，绘制钢材的几何模型。

可以通过三维建模软件创建几何模型，也可以通过Abaqus软件中的几何建模功能直接创建几何模型。

2. 定义材料属性和本构模型：在建模过程中，需要定义材料的力学特性和选择合适的本构模型。

可根据前文所述的步骤进行定义。

3. 定义边界条件：根据实际需求，定义钢材的边界条件。

这些条件可以包括拉伸速度、约束条件、初始应力等。

2011年7月第27卷第4期沈阳建筑大学学报（自然科学版）Journal of Shenyang Jianzhu University （Natural Science ）Jul ．2011Vol ．27，No ．4收稿日期：2010－12－31基金项目：住房和城乡建设部科技基金项目（2008－K1－15）作者简介：王强（1971—），男，副教授，博士，主要从事工程结构抗震研究．文章编号：2095－1922（2011）04－0679－06用于ABAQUS 显式分析梁单元的混凝土单轴本构模型王强，潘天林，刘明，李哲（沈阳建筑大学土木工程学院，辽宁沈阳110168）摘要：目的为实现采用梁单元进行钢筋混凝土杆系结构的弹塑性响应分析，对其混凝土本构关系进行二次开发，使ABAQUS 软件提供的混凝土材料模型能用于三维梁单元．方法利用ABAQUS 用户自定义材料程序VUMAT 接口，开发用于显式动力分析的梁单元混凝土单轴本构模型，并编制相应的计算程序，对低周往复加载下的钢筋混凝土柱进行数值模拟计算．结果数值模拟结果能够较好地反映轴力对钢筋混凝土构件滞回性能的影响以及钢筋混凝土柱的双向弯曲耦合性能．结论笔者所开发的混凝土本构模型能够用于多维受力状态下钢筋混凝土梁柱构件的受力行为分析，满足钢筋混凝土杆系结构动力弹塑性分析的需求．关键词：混凝土；滞回性能；本构模型；ABAQUS ；VUMAT 中图分类号：TU375.3文献标志码：AStudy on a Uniaxial Constitutive Model of Concrete for Explicit Dynamic Beam Elements of ABAQUSWANG Qiang ，PAN Tianlin ，LIU Ming ，LI Zhe（School of Civil Engineering ，Shenyang Jianzhu University ，Shenyang ，China ，110168）Abstract ：In order to use the beam element of FEM software ABAQUS for analyzing the elastic-plastic dy-namic response of RC truss structures ，it is necessary to carry out a secondary development of the concrete constitutive for spatial beam element．In this paper ，a uniaxial constitutive model of concrete is established．The material subroutine of this model is successfully developed and applied to explicit dynamic module ofABAQUS by means of user-defined subroutine interface VUMAT．Afterwards ，the hysteretic performance of RC columns under cyclic loading is numerically simulated and compared with experiment results．The results show that the uniaxial constitutive model can rightly simulate the influence on the hysteretic performance of RC columns under varies axial load ，as well as the bi-axes bending coupling performance．The established model can meet the demand of analyzing the elastic-plastic dynamic response of RC frame structures．Key words ：concrete ；hysteretic performance ；constitutive model ；ABAQUS ；VUMAT混凝土结构在大震作用下通常会进入塑性状态，采用弹性分析方法进行结构的受力分析不能真实反映结构实际受力情况．进行结构的动力弹塑性响应分析，特别是基于构件材料层次分析模型的弹塑性响应分析，能够较为准确地把握结构在大震作用下的非线性形态，对于评估结构的抗680沈阳建筑大学学报（自然科学版）第27卷震安全性具有重要意义．目前各国学者及工程界已开始致力于此方面的研究［1－4］．通用有限元软件ABAQUS 具有较好的计算稳定性、丰富的单元材料模型以及强大的前后处理功能，目前已在结构构件的非线性分析中得到了广泛的应用［5－7］，特别是其显式分析模块（ABAQUS /EXPLICIT ），由于其采用中心差分法求解动力平衡方程，计算中无需形成结构的整体刚度矩阵，具有计算收敛性好的特点，更适于结构动力弹塑性响应分析．但在ABAQUS 显式分析模块中，软件提供的混凝土材料模型不能用于三维梁单元．若采用实体单元进行高层建筑等杆系结构的整体分析，则计算工作量较大，难以满足工程计算需求．笔者基于纤维模型［8］，利用ABAQUS 显式分析模块的用户自定义材料子程序VU-MAT ，对梁单元的混凝土材料模型进行二次开发，以满足结构动力弹塑性响应分析的需求．1纤维梁单元模型基于材料单轴本构关系的纤维模型是将构件沿纵向划分为若干子段，再沿构件横截面划分成纤维束．每个纤维只考虑它的轴向本构关系，且可定义不同的本构关系．柱横截面变形符合平截面假定．对截面纤维的当前状态积分就可以得到截面的双向抗弯刚度、双向抵抗矩以及轴力，进而沿杆长进行积分，就可以得到精确的杆件单元刚度矩阵．纤维模型可以自然、简单地描述构件的双向弯曲－轴力耦合效应．1.1基本假定（1）构件截面变形满足平截面假定；（2）不考虑钢筋与混凝土之间的相对滑移；（3）不考虑构件的剪切非线性及与其他变形的耦合关系．1.2单元截面刚度矩阵梁单元类型为ABAQUS 显式分析模块中的B31梁单元［9］．该单元是基于铁摩辛柯（Timosh-enko ）梁理论构建的，可以考虑剪切变形．B31梁单元具有两个节点，一个积分点，转角和位移采用线性插值，如图1（a ）所示．采用GREEN 应变计算公式，可考虑大应变．单元质量阵为对角阵形式．采用矩形梁截面描述构件截面中的混凝土部分，将其划分为25个积分点或更多，如图1（b ）所示；同时采用箱型截面按等面积原则、等位置代替截面中的钢筋，划分为16个积分点或更多，如图1（c ）所示．每个积分点即为一个纤维．图1B31梁单元的积分点设置Fig.1Integration points of B31beam element假设梁单元的横截面坐标轴分别为y 、z 轴，纵向坐标轴为x 轴．由单元节点位移通过插值函数可以得到轴向积分点处变形向量d （x ）=｛Φz （x ）Φy （x ）ε0（x ）｝T ．（1）根据截面积分点的位置，由轴向积分点处变形向量可以得到纤维的应变向量ε（x ）25ˑ1=H 25ˑ3d （x ）．（2）其中截面纤维几何位置转换矩阵H =［H 1H 2…H 25］T，H i =［－y iz i1］，i =1，2， (25)由纤维的应变向量与材料的本构关系可得截面应力向量σ=E ε，其中E 为纤维切线刚度对角阵．截面恢复力向量F （x ）=｛M zM yN ｝T =H T A σ=H T AE ε=H T AEH d （x ）．（3）式中：M z ，M y ，N 分别为截面上绕y 、z 轴的弯矩及轴向力；A 为纤维面积对角阵．整理可得单元截面的刚度矩阵为K sec =H T AEH ．（4）运用单元形函数矩阵，可以从截面刚度矩阵推得单元刚度矩阵K e =∫lB T KsecB d x．式中，B 为单元形函数矩阵，l 为单元长度．第27卷王强等：用于ABAQUS 显式分析梁单元的混凝土单轴本构模型6812材料的本构模型2.1钢筋的本构模型钢筋在反复荷载作用下本构模型采用ABAQUS 中自带的随动强化模型［9］，并考虑钢筋屈服硬化，钢筋屈服后刚度取E =0.01E 0，对应的单轴本构模型如图2所示．其中E 0为初始弹性模量，E 为屈服后弹性模量，f y 为屈服应力，εy 为屈服应变．图2钢筋的本构模型Fig.2Constitutive model of steel2.2混凝土的本构模型笔者采用基于文献［10］提出的混凝土本构模型，如图3所示．其中E c 0为原点切线模量；E cr 为损伤后弹性模量；εcm 为混凝土所经历的最大压应变；f c 为混凝土抗压强度；ε0为混凝土峰值应力所对应的应变，ε0=0.002；εu 为混凝土的极限压应变，εu =4ε0．混凝土受压骨架曲线采用Kent 和Park 所提出并由B．D．Scott 改进的混凝土应力－应变曲线［11］．由于混凝土的抗拉强度很低，且在滞回过程中一旦开裂，混凝土就不能再承受拉力，因此抗拉强度对混凝土构件滞回性能影响较小［12－13］．故在本构模型中忽略混凝土的抗拉强度，并忽略裂面效应影响．混凝土卸载及再加载曲线均取为直线形式．卸载时考虑刚度的退化，卸载模量按式（7）确定：E cr =E c0εc ≤ε0，E c0ε0ε()cm0.9εc ＞ε0{．（7）当混凝土卸载至零压应力时，如继续卸载则材料应力保持为零．若混凝土卸载至零压应力之前又开始加载，则沿原路径返回．再加载时加载曲线始终指向骨架曲线上所经历的最大应变点．若应力超过骨架曲线上的相应点，则沿骨架曲线加载．若混凝土应力在达到骨架曲线之前开始卸载，则按照所经历的最大压应变来确定卸载刚度．图3混凝土的本构模型Fig.3Constitutive model of concrete3用户自定义材料子程序（VU-MAT ）实现依据前述的混凝土本构模型，笔者基于用户自定义材料子程序VUMAT 接口，编制了计算程序，并嵌入ABAQUS /EXPLICIT 模块中［9］．主程序通过ABAQUS 输入文件中的关键字“*USER-MATERIAL ”来判断是否使用了用户自定义材料，并提供混凝土本构模型所需的材料参数［11］．在ABAQUS 中对编制的VUMAT 子程序进行调试，来跟踪每一步调用子程序时变量的更新情况，从而及时发现所产生的错误．调试时要在com-mand 窗口中输入“abaqus －j 文件名．inp －user程序名．for －debug －explicit ”，在VISUAL STU-DIO 开发环境中打开子程序，然后设置断点进行调试．在VUMAT 中只有程序中定义的数组和变量能够进行新旧变量更替，如果另定义更新变量必须特别声明存储特性，否则子程序不会保存上一步变量数值．编程中还应避免除零问题．为保证程序编制思路的可靠性，笔者在进行混凝土本构模型开发之前，首先编制了理想弹塑性材料的VUMAT ，并与ABAQUS 自带理想弹塑性模型进行对比，得到的结果基本一致．4算例验证为充分验证模型的有效性，笔者分别对不同加载制度下的钢筋混凝土柱滞回性能进行计算分析．试件情况见文献［14］，构造和配筋如图4所682沈阳建筑大学学报（自然科学版）第27卷示．各试件的加载规则见表1，其中试件SP1与SP2为笔者构造的加载制度，SP3与SP4则为文献［14］中的试件TP74和TP77．材料参数取值见表2．图4钢筋混凝土柱试件Fig.4Reinforced concrete column specimens表1算例加载制度Table 1Loading pattern of example试件编号加载图示加载规则轴力/kN备注SP1－轴向往复加载SP20无轴压单向往复侧推SP3160有轴压单向往复侧推SP4160有轴压双向往复侧推表2材料基本参数Table 2Basic parameters of materials参数项屈服强度/MPa 屈服应变泊松比弹性模量/104MPa 混凝土29．660．0020．252钢筋3570．00170．320由于采用显式动力方法进行拟静力分析，必须减小惯性力对整个构件的影响．采取的措施是降低加载速率和减小计算时步，这样可以使加速度趋近于很小，从而忽略惯性力影响．图5为计算所得试件SP1在轴向往复拉压时，ABAQUS 计算输出的角部混凝土纤维受压应力应变曲线（压为负）．该曲线符合笔者所给出混凝土的本构模型，表明笔者编制的材料本构子程序是正确的．图6为试件SP2计算所得的水平加载滞回曲线．可以看出无轴压时构件的滞回曲线呈梭形，且较为饱满，属于典型的受弯构件滞回性能［15］．而且对试验的“超前指向”现象也有所表现，即加载曲线并不指向前一循环的开始卸载点，而是指向前一循环的开始卸载点位移更大的一点．图5试件SP1角部混凝土纤维的应力应变关系Fig.5Stress-strain relationship of corner concrete fiber of specimenSP1图6试件SP2计算所得滞回曲线Fig.6Calculated hysteresis curve of specimen SP2图7、8分别为试件SP3的试验实测与计算所得滞回曲线，二者对比可以发现在加载初期0 20mm 时实验曲线与计算曲线基本一致，只是峰值点处计算值略小，这可能是对于混凝土受箍筋第27卷王强等：用于ABAQUS 显式分析梁单元的混凝土单轴本构模型683约束使得强度提高考虑不足．在后期加载20 60mm 时，计算所得滞回曲线较为丰满．造成此现象的原因主要是没有考虑钢筋的滑移，特别是加载后期实际构件已产生滑移，而计算模型并没有表现出来．而且采用的钢筋本构模型为线性强化模型，与真实钢筋的本构关系有一定误差，耗能能力更强一些，所以导致计算所得的滞回曲线比试验所得的曲线要饱满一些．对于试验结果中的“超前指向”现象，计算结果同样能够予以较好的描述．此外由图8与图6对比可以看出轴压力的存在使得构件极限承载力略有提高，而滞回曲线产生捏拢现象．图7试件SP3实测滞回曲线Fig.7Hysteresis curve of specimenSP3图8试件SP3计算所得滞回曲线Fig.8Calculated hysteresis curve of specimen SP3图9、10分别为试件SP4的实验与计算结果．由计算结果可以看出，当方向1保持位移恒定，方向2的加载使得方向1产生荷载跌落现象，反之亦然，这在试验曲线中有相应的体现．可以认为计算模型能够较好地反映钢筋混凝土柱的双向弯曲耦合性能．计算所得滞回曲线仍较试验曲线丰满，计算峰值略低于实验值．图9SP4试验滞回曲线Fig.9Hysteresis curve ofSP4图10SP4计算滞回曲线Fig.10Calculated hysteresis curve of SP4684沈阳建筑大学学报（自然科学版）第27卷5结论（1）笔者建立的模型可以正确反映轴力对钢筋混凝土构件滞回性能的影响，能够较好地模拟钢筋混凝土柱的双向弯曲耦合性能以及滞回曲线中的超前指向与捏拢现象，可以用于多维受力状态下钢筋混凝土梁柱构件的受力行为分析，能够满足空间框架结构动力弹塑性分析的需求．（2）采用箱型截面等效代替考虑钢筋混凝土杆件中的钢筋，有效地解决了杆件采用梁单元模型时难以考虑钢筋作用的问题．（3）由于采用的模型未考虑钢筋的滑移，对整个结果的精确性有一定的影响，有待于进一步研究．参考文献：［1］秦从律，张爱晖．基于截面纤维模型的弹塑性时程分析方法［J］．浙江大学学报，2005（7）：1003－1008．（Qin Conglü，Zhang Aihui．Non linear time historyanalysis based on section fiber model［J］．Journal ofZhejiang University（Engineering Science），2005（7）：1003－1008．）［2］Li Kangning．3-D Analysis of RC f rame-w al l building damaged in the1995hyogoken-nanbu earth-quake［C］//Process of the12th World Conference onEarthquake Engineering，New Zealand：Auckland，2000．［3］Mazzoni S，Mckenna F，Scott M H，et al．Opensees command language manual［R］．PEER，Berkeley：U-niversity of California，2004．［4］汪训流，陆新征，叶列平．往复荷载下钢筋混凝土柱受力性能的数值模拟［J］．工程力学，2007（12）：76－81．（Wang Xunliu，Lu Xinzheng，Ye Lieping．Numericalsimulation for the hysteresis behavior of RC columnsunder cyclic loads［J］Engineering Mechanics，2007，24（12）：76－81．）［5］王金昌，陈页开．ABAQUS在土木工程中的应用［M］．杭州：浙江大学出版社，2006．（Wang Jinchang，Chen Yekai．Application ofABAQUS in civil engineering［M］．Hangzhou：Zhe-jiang University Press，2006．）［6］Navalurkar R K，Hsu C T．Fracture analysis of high strength concrete members［J］．Journal of Materialsin Civil Engineering，2001，13（3）：185－193．［7］Chung W，Sotelino E D．Nonlinear finite-element a-nalysis of composite steel girder bridges［J］．Journalof Structural Engineering，2005，131（2）：304－313．［8］Spacone E，Fillippou F C，Taucer F．Fiber beam-col-umn model for non-liner analysis of R/C frames［J］．Journal of Earthquake Engineering and Structur-al Dynamics，1996，25：711－725．［9］庄茁，由小川，廖剑辉，等．基于ABAQUS的有限元分析和应用［M］．北京：清华大学出版社，2009．（Zhuang Zhuo，You Xiaochuan，Liao Jianhui，et al．FEM analysis and application based on ABAQUS［M］．Beijing：Tsinghua University Press，2009．）［10］王强，吕西林，雷淑忠．离散单元法在钢筋混凝土构件非线性分析的应用［J］．沈阳建筑大学学报：自然科学版，2005（2）：91－95．（Wang Qiang，Lu Xilin，Lei Shuzhong．Applicationof the DEM on the nonlinear analysis of reinforcedconcrete members［J］．Journal of Shenyang JianzhuUniversity：Natural Science，2005（2）：91－95．）［11］Scott B D，Park R，Priestley M J N．Stress-strain be-havior of concrete confined overlapping hoops at lowand high strain rates［J］．ACI Journal，1982，79（1）：13－27．［12］Légeron F，Paultre P．Uniaxial confinement model for normal and high-strength concrete columns［J］．Jour-nal of Structural Engineering，2003，129（2）：241－252．［13］Mander J B，Priestley M J N，Park R．Theoretical stress-strain model for confined concrete［J］．Journalof Structural Engineering，1988，114（8）：1804－1825．［14］Kawashima K，Watanabe G，Hayakawa R．Seismic performance of RC bridge columns subjected to bi-lateral excitation［C］//Proc．35th joint meeting，pan-el on wind and seismic effects，Japan：Tsukuba Sci-ence City，2003．［15］张新培．钢筋混凝土抗震结构非线性分析［M］．北京：科学出版社，2003．（Zhang Xinpei．Nonlinear seismic study on rein-forced concrete structures［M］．Beijing：SciencePress，2003．）。

abaqus材料库Abaqus材料库。

Abaqus是一款广泛应用于工程领域的有限元分析软件，它的材料库包含了各种工程材料的力学性能数据，为工程师和研究人员提供了便利的材料选择和建模分析工具。

本文将介绍Abaqus材料库的基本内容和使用方法。

Abaqus材料库包括金属材料、塑料材料、复合材料、岩土材料等各种类型的材料数据。

用户可以在Abaqus的材料库中选择合适的材料模型，并根据实际工程需求进行参数调整和修改。

在建模分析过程中，选择合适的材料模型对于模拟结果的准确性和可靠性至关重要。

在Abaqus中，对于金属材料，可以选择各种常见的本构模型，如线弹性模型、非线性弹性模型、塑性本构模型等。

用户可以根据材料的真实力学性能数据，选择合适的本构模型，并进行参数的校准和调整，以保证模拟结果的准确性。

对于塑料材料，Abaqus提供了各种常见的本构模型，如线性弹性模型、非线性弹性模型、弹塑性本构模型等。

用户可以根据材料的拉伸、压缩、剪切等力学性能数据，选择合适的本构模型，并进行参数的校准和调整，以保证模拟结果的准确性。

对于复合材料，Abaqus提供了各种常见的层合板材料模型，用户可以根据复合材料的层合板结构和材料性能数据，选择合适的层合板材料模型，并进行参数的校准和调整，以保证模拟结果的准确性。

对于岩土材料，Abaqus提供了各种常见的本构模型，用户可以根据岩土材料的力学性能数据，选择合适的本构模型，并进行参数的校准和调整，以保证模拟结果的准确性。

在使用Abaqus材料库时，用户需要充分了解材料的力学性能数据和本构模型的特点，合理选择合适的材料模型，并进行参数的校准和调整。

在建模分析过程中，需要对模型的材料属性进行合理的设置和调整，以保证模拟结果的准确性和可靠性。

同时，用户还需要对模型的边界条件、加载方式等进行合理的设置和调整，以保证模拟结果的真实性和可靠性。

总之，Abaqus材料库为工程师和研究人员提供了丰富的材料模型和力学性能数据，为工程建模分析提供了便利的工具和支持。

各向同性材料损伤本构模型SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD,+ RPL,DDSDDT,DRPLDE,DRPLDT,+ STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME, + NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT, + CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,KSTEP,KINC)INCLUDE 'ABA_PARAM.INC'CHARACTER*80 CMNAMEDIMENSION STRESS(NTENS),STATEV(NSTATV),+ DDSDDE(NTENS,NTENS),DDSDDT(NTENS),+ DRPLDE(NTENS),STRAN(NTENS),DSTRAN(NTENS),+ TIME(2),PREDEF(1),DPRED(1),PROPS(NPROPS),+ COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3)DIMENSION STRANT(6),TSTRANT(4),PT(1)DIMENSION OLD_STRESS(6)DIMENSION DOLD_STRESS(6),D_STRESS(6)DIMENSION C(6,6),CD(6,6),DSTRESS(6),BSTRESS(6),ROOT(3),+ DFMNDE(6),DDMDE(6),DCDDM(6,6),ATEMP1(6), ATEMP2(6)PARAMETER (ZERO=0.D0,ONE=1.D0,TWO=2.D0,FOUR=4.D0,HALF = 0.5D0) C startC IF (NPROPS.LT.2) THENC WRITE(7,*) '** ERROR: UMAT REQUIRES *NPROPS=2'C STOPC END IFE11 =PROPS(1)V12 =PROPS(2)G12 =PROPS(1)/TWO/(ONE+PROPS(2))C Critical values of streSSEsXT=PROPS(3)XC=PROPS(4)XS=PROPS(5)GX=PROPS(6) !Fracture energy in matrixETA=0.001C Current strainDO I = 1, NTENSSTRANT(I) = STRAN(I) + DSTRAN(I) END DOC StiffnessDO I = 1, 6DO J = 1, 6C(I,J)=ZEROEND DOEND DOATEMP = (1+V12)*(1-TWO*V12)C(1,1) = E11*(1-V12)/ATEMPC(2,2) = E11*(1-V12)/ATEMPC(3,3) = E11*(1-V12)/ATEMPC(1,2) = E11*V12/ATEMPC(1,3) = E11*V12/ATEMPC(2,3) = E11*V12/ATEMPC(4,4) = G12C(5,5) = G12C(6,6) = G12DO I = 2, 6DO J = 1, I-1C(I,J) = C(J,I)END DOEND DOC Critical values of strainsXET=XT/(C(1,1)-2*V12*C(1,2))XEC=XC/(C(1,1)-2*V12*C(1,2))XES=XS/C(4,4)DMOLD = STATEV(1)C Strain initiation criterionA11 = STRANT(1)**TWO+STRANT(2)**TWO+STRANT(3)**TWO A12 = A11 / XET / XECA21 = STRANT(1)+STRANT(2)+STRANT(3)A22 = (XEC - XET) / XEC / XET * A21A31 = STRANT(4)**TWO+STRANT(5)**TWO+STRANT(6)**TWO A32 = A31 / XES**TWOA1= A12 + A22 + A32C B11 = STRANT(2)**TWOC B12 = B11 / XET / XECC B21 = STRANT(2)C B22 = (XEC - XET) / XEC / XET * B21C B31 = STRANT(5)**TWOC B32 = B31 / XES**TWOC B1= B12 + B22 + B32C C11 = STRANT(3)**TWOC C12 = C11 / XET / XECC C21 = STRANT(3)C C22 = (XEC - XET) / XEC / XET * C21C C31 = STRANT(6)**TWOC C32 = C31 / XES**TWOC C1= C12 + C22 + C32STATEV(2)=A1C STATEV(3)=B1C STATEV(4)=C1FMN = ZEROIF (A1.GT.ZERO) THEN FMN =SQRT(A1)C IF (B1.GT.ONE) THEN C FMN =FMN+SQRT(B1) C IF(C1.GT.ONE) THEN C FMN =FMN+SQRT(C1)C END IFC END IFEND IFSTATEV(5)=FMNC write(*,*) FMNDM = ZERODDMDFMN = ZERODO I = 1, 6DFMNDE(I) = ZERODDMDE(I) = ZEROEND DOIF (FMN .GT. ONE) THENC CALCULATE DM, DDMDFMNC WRITE(6,*)FMNT1 = (C(1,1)-2*V12*C(1,2)) * XET**2 * CELENT / GXT2 = (ONE - FMN) * T1DM = ONE - EXP(T2)/FMNC WRITE(6,*)'T1 ',T1,' T2', T2, ' DM', DMC write(*,*) DMC CALCULATE THE DERIVATIVE OF DAMAGE VARIABLE WITH RESPECT TO FAILURE C RITERIONDDMDFMN = (ONE / FMN + T1) * (ONE - DM)C CALCULATE DFMNDEIF (DM .GT. DMOLD) THENDFMNDE(1) = HALF/FMN*(TWO*STRANT(1)+XEC-XET)/XET/XEC DFMNDE(2) = HALF/FMN*(TWO*STRANT(2)+XEC-XET)/XET/XEC DFMNDE(3) = HALF/FMN*(TWO*STRANT(3)+XEC-XET)/XET/XEC DFMNDE(4) = ONE/FMN*TWO*STRANT(4)/XES**TWODFMNDE(5) = ONE/FMN*TWO*STRANT(5)/XES**TWODFMNDE(6) = ONE/FMN*TWO*STRANT(6)/XES**TWODO I = 1, 6DDMDE(I) = DFMNDE(I) * DDMDFMNEND DOEND IFEND IFDM = MAX (DM, DMOLD)C write(6,*) DMC SAVE THE OLD STRESS TO OLD_STRESSDO I = 1, NTENSOLD_STRESS(I) = STRESS(I) END DOC Effective stiffnessDO I = 1, 6DO J = 1, 6CD(I,J)=C(I,J)END DOEND DOIF (DM.NE.ZERO) THENCD(1,1) = (ONE - DM)*C(1,1) CD(1,2) = (ONE - DM)*C(1,2) CD(2,1) = CD(1,2)CD(2,2) = (ONE - DM)*C(2,2) CD(1,3) = (ONE - DM)*C(1,3) CD(3,1) = CD(1,3)CD(2,3) = (ONE- DM)*C(2,3)CD(3,2) = CD(2,3)CD(4,4) = (ONE - DM)*C(4,4) CD(5,5) = (ONE - DM)*C(5,5) CD(6,6) = (ONE - DM)*C(5,5) END IFC Elastic derivativeDO I = 1, 6DO J = 1, 6DCDDM(I,J) = ZEROEND DOEND DOCC CALCULATE DC/DDMCDCDDM(1,1) = -C(1,1) DCDDM(1,2) = -C(1,2) DCDDM(2,1) = -C(2,1)DCDDM(2,2) = -C(2,2)DCDDM(2,3) = -C(2,3)DCDDM(3,2) = -C(3,2)DCDDM(3,3) = -C(3,3)DCDDM(3,1) = -C(3,1)DCDDM(1,3) = -C(1,3)DCDDM(4,4) = -C(4,4)DCDDM(5,5) = -C(5,5)DCDDM(6,6) = -C(6,6)C UPDATE THE JACOBIANDO I = 1, NTENSATEMP1(I) = ZERODO J = 1, NTENSATEMP1(I) = ATEMP1(I) + DCDDM(I,J) * STRANT(J) END DOEND DODDSDDE=0DO I = 1, NTENSDO J = 1, NTENSDDSDDE(I,J)=CD(I,J)+(ATEMP1(I)*DDMDE(J))*DTIME/(DTIME+ETA) END DO END DOC Update streSSEsDO I = 1, NTENSSTRESS(I)=ZERODO J = 1, NTENSC IF(DM.LT.0.5) THENSTRESS(I)=STRESS(I)+ CD(I,J) * STRANT(J)C ELSEC STRESS(I)=STRESS(I)+ CD(I,J) * STRANT(J) * (1-DM)C ENDIFEND DOEND DOC EnergyDO I = 1, NDISSE = SSE + HALF * (STRESS(I) + OLD_STRESS(I)) * DSTRAN(I) END DO DO I = NDI+1, NTENSSSE = SSE + (STRESS(I) + OLD_STRESS(I)) * DSTRAN(I)END DOSTATEV(1)=DMRETURNEND。

ABAQUS-材料本构模型及编程材料本构模型及编程-ABAQUS-UMAT材料本构模型及编程实现：简介1、什么时候用用户定义材料（User-defined material,UMAT）？很简单，当ABAQUS没有提供我们需要的材料模型时。

所以，在决定自己定义一种新的材料模型之前，最好对ABAQUS已经提供的模型心中有数，并且尽量使用现有的模型，因为这些模型已经经过详细的验证，并被广泛接受。

2、好学吗？需要哪些基础知识？先看一下ABAQUS手册（ABAQUS Analysis User's Manual）里的一段话：Warning:The use of this option generally requires considerable expertise.The user is cautioned that the implementation of any realistic constit utive model requires extensive development and testing.Initial testing on a single element model with prescribed traction loading is strongly rec ommended.但这并不意味着非力学专业，或者力学基础知识不很丰富者就只能望洋兴叹，因为我们的任务不是开发一套完整的有限元软件，而只是提供一个描述材料力学性能的本构方程（Constitutive equation）而已。

当然，最基本的一些概念和知识还是要具备的，比如应力(stress),应变（strain）及其分量；volumetric part和deviatoric part；模量（modulus）、泊松比(Poisson’s ratio)、拉美常数(Lame constant)；矩阵的加减乘除甚至求逆；还有一些高等数学知识如积分、微分等。