小学数学四年级上册数学广角优化烙饼问题
- 格式:pptx
- 大小:2.31 MB
- 文档页数:17

广角优化烙饼问题是一道经典的数学问题,其核心思想是通过翻转烙饼的顺序来达到最优解,以下是一些优化烙饼问题的解题技巧:
1.一般来说,如果有n个烙饼,需要翻转n次才能将它们全部翻到正面。
因此,
我们可以将翻转次数的上限设为2n,如果在这个上限内没有找到最优解,则可以认为无解。
2.在每次翻转过程中,我们可以将烙饼中最大的烙饼翻到最上面,然后再将整
个烙饼序列翻转一次,这样可以将最大的烙饼翻到最下面,从而实现排序的效果。
3.在翻转烙饼的过程中,我们可以使用递归算法,将问题分解为更小的子问题。
例如,将n个烙饼排序可以分解为将n-1个烙饼排序和一次翻转操作,然后再将n-1个烙饼排序即可。
4.在实际操作中,我们可以使用烙饼夹子等工具来辅助翻转烙饼,使操作更加
方便和高效。
总之,广角优化烙饼问题是一道有趣的数学问题,通过巧妙的思路和技巧,可以实现高效的烙饼排序。





四年级上册数学教案:数学广角——优化《烙饼问题》一、教学目标1. 让学生理解“烙饼问题”的含义,掌握解决烙饼问题的基本方法。
2. 培养学生运用优化思想解决问题的能力,提高学生的数学思维。
3. 培养学生合作交流、动手操作的能力,激发学生学习数学的兴趣。
二、教学内容1. 烙饼问题的含义及解决方法。
2. 烙饼问题的优化思想。
三、教学重点与难点1. 教学重点:理解并掌握烙饼问题的解决方法,能够运用优化思想解决实际问题。
2. 教学难点:理解优化思想,并能将其应用于解决烙饼问题。
四、教学过程1. 导入新课- 利用生活中的实例引入烙饼问题,激发学生的兴趣。
- 提问:同学们,你们在生活中遇到过烙饼问题吗?知道怎样解决吗?2. 探究新知- 讲解烙饼问题的含义,让学生明确什么是烙饼问题。
- 引导学生思考如何解决烙饼问题,让学生自主探究解决方法。
- 分组讨论,让学生在合作中交流想法,共同解决问题。
3. 课堂讲解- 对学生的解决方法进行点评,总结出最优解法。
- 引导学生理解优化思想,让学生明白如何用优化思想解决问题。
- 通过例题讲解,让学生掌握解决烙饼问题的步骤和方法。
4. 巩固练习- 设计不同层次的练习题,让学生独立完成,巩固所学知识。
- 对学生的练习情况进行点评,及时纠正错误,巩固正确解法。
5. 课堂小结- 让学生回顾本节课所学内容,总结烙饼问题的解决方法及优化思想。
- 强调优化思想在解决实际问题中的应用价值。
五、作业布置1. 请同学们回家后,向家长讲解什么是烙饼问题,并展示解决方法。
2. 完成课后练习题,巩固所学知识。
六、教学反思本节课通过生活中的实例引入烙饼问题,激发学生的兴趣,让学生在合作中探究解决方法,培养学生的合作交流能力和动手操作能力。
在讲解过程中,注重引导学生理解优化思想,让学生明白如何用优化思想解决问题。
通过本节课的学习,希望学生能够掌握烙饼问题的解决方法,提高解决实际问题的能力。
在教学过程中,需要重点关注的是“探究新知”环节。


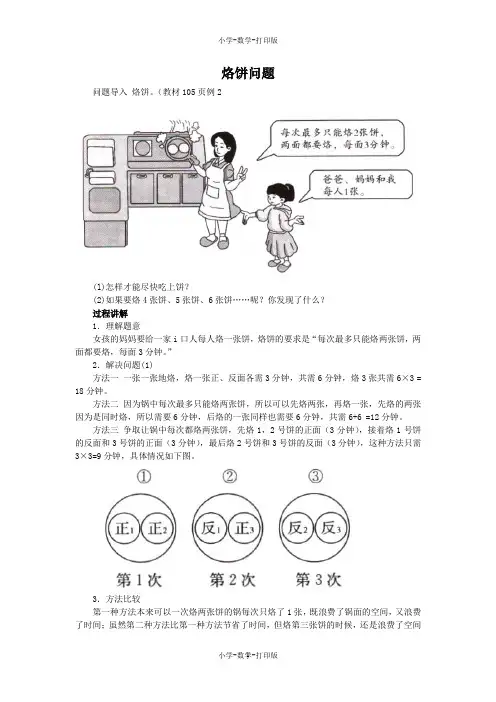
烙饼问题问题导入烙饼。
(教材105页例2(l)怎样才能尽快吃上饼?(2)如果要烙4张饼、5张饼、6张饼……呢?你发现了什么?过程讲解1.理解题意女孩的妈妈要给一家i口人每人烙一张饼,烙饼的要求是“每次最多只能烙两张饼,两面都要烙,每面3分钟。
”2.解决问题(1)方法一一张一张地烙,烙一张正、反面各需3分钟,共需6分钟,烙3张共需6×3 = 18分钟。
方法二因为锅中每次最多只能烙两张饼,所以可以先烙两张,再烙一张,先烙的两张因为是同时烙,所以需要6分钟,后烙的一张同样也需要6分钟,共需6+6 =12分钟。
方法三争取让锅中每次都烙两张饼,先烙1,2号饼的正面(3分钟),接着烙1号饼的反面和3号饼的正面(3分钟),最后烙2号饼和3号饼的反面(3分钟),这种方法只需3×3=9分钟,具体情况如下图。
3.方法比较第一种方法本来可以一次烙两张饼的锅每次只烙了1张,既浪费了锅面的空间,又浪费了时间;虽然第二种方法比第一种方法节省了时间,但烙第三张饼的时候,还是浪费了空间和时间;只有第i种方法最合理,让锅中每次都烙两张饼,既充分利用了锅面的空间又节省时间。
所以,烙饼的最优方案是第三种方法。
4.解决问题(2)发现:当每次最多只能烙两张饼时,烙饼所需要的最短时间一烙饼张数×烙每面饼所需时间(烙一张除外)。
如:烙5张饼需要的时间:5×3=15(分),烙9张饼需要的时间:9×3=27(分)。
归纳总结无论烙多少张饼,只要保证每次都在锅中放两张饼,就能最节省时间。
如果烙饼的张数是双数,两张两张地烙就可以了;如果烙饼的张数是单数,可以先两张两张地烙,最后3张按“烙3张饼”的最优方案去烙,最节省时间。

四年级上数学广角——优化之烙饼问题在我们四年级上册的数学学习中,有一个非常有趣且实用的内容,那就是“优化之烙饼问题”。
同学们,你们有没有想过,在日常生活中,我们经常会遇到需要合理安排时间、提高效率的情况。
比如妈妈做饭的时候,怎样安排才能在最短的时间内做好一桌美味的饭菜?而烙饼问题,就是这样一个需要我们通过思考和计算来找到最优解决方案的典型例子。
想象一下,现在有一口平底锅,每次最多只能烙两张饼,饼的两面都要烙,每烙一面需要3 分钟。
如果要烙3 张饼,怎样烙才能最快呢?咱们先来一个一个地烙。
先烙第一张饼的正面和反面,需要6 分钟;再烙第二张饼的正面和反面,又需要 6 分钟;最后烙第三张饼的正面和反面,还是 6 分钟。
这样一共需要 18 分钟。
但是,这样是不是最快的方法呢?显然不是。
那咱们换一种思路。
我们可以先烙第一张饼和第二张饼的正面,需要3 分钟;然后烙第一张饼的反面和第三张饼的正面,又需要3 分钟;最后烙第二张饼的反面和第三张饼的反面,还是 3 分钟。
这样一共只需要 9 分钟。
通过对比,我们可以发现,同样是烙 3 张饼,不同的方法所需要的时间竟然相差了 9 分钟!这就充分说明了合理安排的重要性。
那如果要烙 4 张饼呢?我们可以两张两张地烙。
先烙前两张饼,需要 6 分钟;再烙后两张饼,也需要 6 分钟。
一共需要 12 分钟。
如果是 5 张饼呢?我们可以先烙 2 张,再烙 3 张。
烙 2 张需要 6 分钟,烙 3 张按照刚才我们找到的最优方法需要 9 分钟,一共就是 15 分钟。
那如果饼的数量更多呢?其实我们只要找到规律,就能很快算出最短的时间。
当饼的数量是偶数张时,我们就两张两张地烙;当饼的数量是奇数张时,我们先两张两张地烙,剩下的 3 张按照前面说的最优方法烙。
通过这个烙饼问题,我们不仅学会了如何计算最短的烙饼时间,更重要的是,我们学会了运用优化的思想来解决生活中的实际问题。
比如说,在我们做作业的时候,是不是可以先做简单的、自己擅长的科目,然后再集中精力攻克难题?这样是不是就能提高我们完成作业的效率呢?再比如,学校组织活动,需要安排不同的项目和人员,我们也可以运用优化的思想,合理安排时间和资源,让活动能够顺利、高效地进行。

烙饼问题的解答规律(人教版四年级数学上册第七单元数学广角)一、烙饼问题(一)平底锅,每次只能烙两张饼,两面都要烙,每面3分钟,烙三张饼,怎样才能尽快吃上饼?方法一:第一次先烙○1○2号饼的正面;第二次烙○1的反面,○3号饼的正面;第三次烙○2号饼的反面,○3号饼的反面。
这种方案共需时间:3×3=9(分钟)烙的次数是关键如果烙4张、5张、6张、7张、......怎样烙更节省时间?方法二:如果烙的张数是双数,2张2张烙就可以了;如果烙的张数是单数,先2个2个的烙,最后的3张,就按我们前面讲过的“方法一”去烙最节省时间。
方法三(终极规律):烙3张饼,烙3次,3×3=9(分钟)烙4张饼,烙4次,3×4=12烙5张饼,烙5次,3×5=15烙6张饼,烙6次,3×6=18烙7张饼,烙7次,3×7=21烙100张饼,烙100次,3×100=300烙n张饼,烙n次,3×n=看到这里,你也许该明白了吧!(二)平底锅,每次只能烙3张饼,两面都要烙,每面3分钟,烙4张饼,至少需要几分钟?考虑“烙几次”是核心方法一:烙3张饼,烙2次,(3张3张烙)烙4张饼,烙3次,(重点要记住)烙5张饼,烙4次,(重点要记住)烙6张饼,烙4次,(3张+3张烙)(2次+2次)烙7张饼,烙5次,(3张+4张烙)(2次+3次)烙8张饼,烙6次,(3张+5张烙)(2次+4次)烙9张饼,烙6次,(3张+3张+3张)(2次+2次+2次)烙10张饼,烙7次,(3张+3张+4张)(2次+2次+3次)不知道你现在理解了这其中的方法了吗?先3张3张得烙,最后要么剩4张,要么剩5张,一个3张是2次,一个4张是3次,一个5张是4次。
例如,烙100张饼,至少几次?100÷3=32(个)......4(张)32个3张饼,(一个3张是2次)2次×32个=64次,再加上4张饼是3次,共67次三、平底锅,每次只能烙四张饼,两面都要烙,每面3分钟,烙5张,至少需要几分钟?方法:烙5张,烙3次(重点要记住)烙6张,烙3次(重点要记住)烙7张,烙4次(重点要记住)以后的是4张4张的烙,剩5、6、7张记住上边的就行了。
名师总结优秀知识点
第八章数学广角——优化
一、合理安排时间
1、烙饼问题
节省时间的最佳方案是每一次尽可能地让锅里按要求放上最多的饼,这样既没有浪费资源,又节省时间。
(1)在每次只能烙两张饼,两面都要烙的情况下:
①烙3张饼:先烙1,2号饼的正面,接着烙1号饼的反面和3号饼的正面,最后烙2,3号饼的反面。
②烙多张饼:如果要烙的饼的张数是双数,2张2张的烙就可以了;如果要烙的饼的张数是单数,可以先2个2个的烙,最后3张饼按①的方法烙,最节省时间。
(2)烙饼的时间计算:
总时间=饼数×烙每面的时间
2、沏茶问题
解决合理安排的问题需要明确以下内容:
①完成一项工作要做哪些事情
②每项事情各需要多少时间
③合理安排工作的顺序,明白先做什么,后做什么,哪些事情可以同时做。
二、比赛中的策略
在与对方进行比赛时,要详细地分析自己与对方的情况,反复研究各种策略,在所有可能采取的策略中,选择一个利多弊少的最优策略,从而使劣势变为优势,最终取得胜利。
田忌用下等马对齐王的上等马,用上等马对齐王的中等马,用中等马对齐王的下等马。
三场两胜,田忌胜出。