几何画板上机实验素材

几何画板实验报告册几何画板实验报告册一、引言几何画板是一种用于绘制几何图形的工具，它由一个平面板和一些固定在板上的钉子组成。

通过在钉子之间穿线，我们可以创造出各种美丽的几何图形。

本实验报告将介绍几何画板的原理、实验过程以及实验结果，并对其应用进行探讨。

二、实验原理几何画板的原理基于线段之间的连线。

当我们在画板上选择两个钉子，并用线段连接它们时，我们可以得到一条直线。

同样，当我们选择三个钉子并连接它们时，我们可以得到一个三角形。

通过在不同的钉子之间连接线段，我们可以创造出更复杂的几何图形，如四边形、五边形等。

三、实验过程1. 准备实验材料：几何画板、彩色线或线团。

2. 将几何画板放在平坦的桌面上。

3. 选择两个钉子，并在它们之间拉一条线段，得到一条直线。

4. 选择三个钉子，并在它们之间拉线段，得到一个三角形。

5. 继续选择更多的钉子，并在它们之间拉线段，创造出更多的几何图形。

6. 使用不同颜色的线团，使图形更加鲜明。

7. 拍摄实验过程中的照片，以备后续分析。

四、实验结果通过实验，我们创造了多个几何图形，包括直线、三角形、四边形、五边形等。

这些图形在几何学中具有重要的意义，并且在日常生活中也有广泛的应用。

通过使用不同颜色的线团，我们可以使图形更加美观，增加观赏性。

五、实验分析几何画板实验不仅仅是一种简单的娱乐活动，它还有着深远的教育意义。

通过实践操作，我们可以更直观地理解几何学中的基本概念和定理。

例如，在创造三角形的过程中，我们可以体验到三条边之间的关系，从而更深入地理解三角形的性质。

此外，几何画板实验还培养了我们的观察力和创造力，激发了我们对几何学的兴趣。

六、应用探讨几何画板不仅可以用于教学和学习，还可以应用于其他领域。

例如，在建筑设计中，几何画板可以帮助建筑师绘制精确的图纸，并确保建筑结构的几何形状符合要求。

在艺术创作中，几何画板可以成为艺术家创作灵感的来源，帮助他们创造出独特而美丽的几何艺术作品。

_____梯形的面积推导公式____实验报告姓名学号日期指导教师实验项目设计一个“梯形面积推导公式”的演示一、上机实验的问题和要求（需求分析）：用几何画板设计一个“梯形面积推导公式”的演示。

二、程序设计的基本思想，原理和算法描述：1、打开打开几何画板，建立新绘图2、画两个全等的梯形用【文字工具】在画板上输入“梯形的面积公式推导”----用【线段直尺工具】画一个梯形ABCD----用【点工具】在空白处画一点E----选中点E和线段BC构造圆----用【点工具】在圆上画一点F----构造线段EF----度量∠ABC的度数----选中点E标记中心----选中EF旋转----标记角度单击参数----选中点E 和线段AB构造圆----选中新线段和新圆构造交点G----隐藏新线段和新圆----构造线段EG----度量∠DAB的度数----选中点G标记中心----选中EG旋转----标记角度单击参数----选中点G和线段AD构造圆----选中新线段和新圆构造交点H----隐藏新线段和新圆----构造线段GH和线段FH3、做运动的梯形选中点E和线段BC构造平行线----选中圆和平行线构造交点1和2----选择点E和点B编辑操作类按钮移动----标签：移动E→B----选择点F和点1 编辑操作类按钮移动----标签：旋转----选中点E和点A 编辑操作类按钮移动----标签：移动E→A----依次选择三个按钮（移动E→B--旋转--移动E→A）编辑操作类按钮系列----标签：移动----选择点F和点2编辑操作类按钮移动----标签：旋转还原----在空白处画一点3----选择点E和点3编辑操作类按钮移动----标签：移动E→3----隐藏点123----依次选择三个按钮（移动E →B--旋转还原--移动E→3）编辑操作类按钮系列----标签：还原----隐藏前三个按钮和一些不用的东西三、调试和运行程序过程中产生的问题及采取的措施：制作系列按钮时要按顺序依次选定按钮四、源程序及注释：五、运行输出结果及分析：。

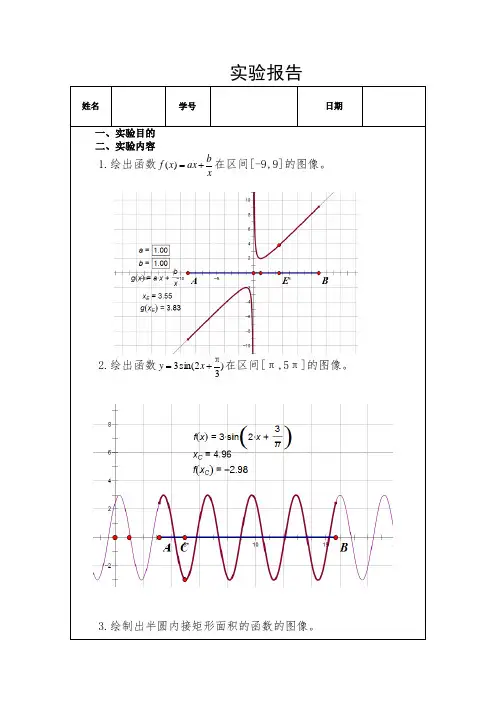
实验报告姓名学号日期一、实验目的 二、实验内容1.绘出函数xb ax x f +=)(在区间[-9,9]的图像。

2.绘出函数)32sin(3π+=x y 在区间[π,5π]的图像。

3.绘制出半圆内接矩形面积的函数的图像。

4.绘制出函数()⎩⎨⎧<<-<<+=.05,sin 30,4x x x x x y 的图像。

5.已知21A F ，分别是椭圆的一焦点与顶点，P 点是椭圆上的一点，求21PA F ∠的最大值。

6.做出半圆沿与BC平行直线DE折叠后重叠部分面积的最大值。

三、实验步骤1.绘出函数xbax x f +=)(在区间[-9,9]的图像。

步骤：①做出点A(-9,0)、B(9,0)，连接AB ，做出函数xbax x g +=)(②在AB 上取一点E ，度量E 的横坐标，计算)(E x g ③做出点（E x ,)(E x g ），选中点E 及（E x ,)(E x g ）做出轨迹2.绘出函数)32sin(3π+=x y 在区间[π,5π]的图像。

步骤：①做出点A(π,0)、B(5π,0)，连接AB ，做出函数)32sin(3π+=x y②在AB 上取一点C ，度量C 的横坐标，计算)(C x f ③做出点（C x ,)(C x f ），选中点C 及（C x ,)(C x f ）做出轨迹3.绘制出半圆内接矩形面积的函数的图像。

步骤：①先以原点为圆心绘制出半圆，接着在半圆上做一点C ，关于Y 轴做出对称点D ，做出半圆的内接矩形CDEF ；②度量出C 点的横坐标，以及矩形CDEF 的面积；③以F 点的横坐标为横坐标，以矩形FGIH 的面积为纵坐标，绘制出点G ； ④选择C ，G 点，利用构造中的轨迹功能，做出半圆内接矩形面积的函数图像。

4. 绘制出函数()⎩⎨⎧<<-<<+=.05,sin 30,4x x x x x y 的图像。

步骤：①做出A （-5，0），B （3，0），连接AB ；做平行与X 轴的直线，过点A ，点O ，点B 做该直线的垂线，交点为E,D,F 点②在线段AB 上任选一点G ，构造线段ED ，过G 点做线段ED 的垂线，垂足为H ；③度量H x ，计算H x sin ，做出点J ）（H H x x sin ,；选择G ，J 点，构造轨迹，即为（-5，0）上x sin 的图像④将点G 移至OB ，构造线段DF ，过点G 做线段DF 的垂线，垂足为K ；⑤度量K x ，计算)4(+K K x x ，做出点L ）（)4(,+K K K x x x ；选择G ，L 点，构造轨迹，即为（3，0）上)4(+x x 的图像；最后移动点G ，可以发现两个图像是一个整体。

几何画板基本操作实验报告一、实验目的1、认识几何画板2、能够使用几何画板的基本绘图工具绘制简单的图形3、掌握动画按钮的制作方法。

二、实验原理通过点的变化来引起动态参数的变化，从而充分体现正弦函数振幅，周期以及初相的变化而引起的函数图像的变化。

三、实验内容绘制函数sin()y A xωφ=+的图像，观察函数的振幅、周期和初象分别与Aωφ、、之间的关系。

四、实验课时：4课时五、实验步骤（略）1、绘制方法：线段坐标法和参数法2、绘制步骤（1）线段坐标法：①新建页：【文件】-【文档选项】-【增加页】-【空白页面】，命名为：三角函数——线段坐标法。

②绘制坐标系：点击【绘图】-【定义坐标系】，右击【隐藏网格】③设置角度单位：【编辑】-【参数选项】，将角度的单位改为【弧度】④选定自变量：在x轴上任取一点F，【度量】-【横坐标】，度量值为X F⑤选取动态的振幅、周期：在x轴上选取两个点H、I，选中两点，点击【变换】→【平移】，固定距离为1厘米，固定角度为90°。

选中H、H’构造射线，并在射线上选取一点，右击此点【属性】-【标签】-（改变振幅A）。

再次选中此点，【度量】-【纵坐标】，并将度量值的标签改为“A”。

选中I、I’构造射线，并在射线上选取一点，右击此点【属性】-【标签】-（改变周期ω）。

再次选中此点，【度量】-【纵坐标】，并将度量值的标签改为“ω”。

⑥选取动态的初相位：选中原点D和单位点E,【构造】-【以圆心和圆周上的点作圆】，【构造】-【圆上的点】，将圆上的点标签改为“改变初相位φ”，依次选中点E、D、改变初相位φ，【度量】-【角度】，将度量的角度值标签改为“φ”。

⑦建立函数并绘制图像：【数据】-【计算】→运用A、ω、φ输入：A*sin(ω*X F+φ)，点击确定。

依次选中X F、Asin(ωX F+φ)，【绘图】-【绘制点（）（P）】，点的标签为“J”，【选中点J】-【选中点F】-【构造】-【轨迹】⑧隐藏不需要显示的对象：选中要隐藏的对象，【编辑】-【操作类按钮】-【显示/隐藏】，点击按钮：【隐藏对象】。

几何画板实验报告————————————————————————————————作者：————————————————————————————————日期：ﻩ几何画板实验报告姓名学号日期一、实验目的:掌握“旋转”与“轨迹”“轨迹”功能及其应用，能熟练将前两者结合绘制复杂图形二、实验内容1. 做出正五边形图形，并将图形沿五边形的中心(1）缩小到原来的１/２（2)扩大到原来的２倍。

2. 绘制五角星并设置控制按钮使其绕中心旋转1８０°。

移动前：移动后：3. 做出把梯形割补成矩形的课件。

移动前：移动后：4.(1）用轨迹功能绘出球面（2）运用缩放、平移、轨迹功能绘出球冠。

三、实验步骤1. 做出正五边形图形，并将图形沿五边形的中心(１）缩小到原来的1／2（2）扩大到原来的2倍。

步骤：①做出线段ＡB,标记中心点B，选中线段AB及点B，旋转10８°得到线段BＣ；同理,标记中心点C，选中线段BC及点C,旋转108°得到线段ＣD。

用同样的方法做出正五边形ABＣDE。

(因正五边形的内角和为3*360°/2=540°，故旋转108°)②选中线段ＡB及点D,构造垂线ｉ,选中线段BC及点Ｅ,构造垂线k。

垂线ｉ与k 相交于点O,即正五边形ABCDE的中心。

③标记中心Ｏ,选中五边形ABＣDＥ与点O,点击缩放，设置缩放比为1.０／2.０,做出缩放图形;再次选中五边形AＢCDＥ与点O，点击缩放,设置缩放比为2.0/1．0，做出放大图形。

２.绘制五角星并设置控制按钮使其绕中心旋转18０°。

步骤:①按照第一题的方法做出正五边形ABCDE及其中心O点。

选中点A与B、点Ｂ与C、点Ｃ与D、点D与E、点Ｅ与A分别构造直线,记交点分别为Ｆ、G、Ｈ、Ｉ、J。

②做出圆P，在圆上任意选中一点Q，做过QP的直线交圆于R点,构造线段QＰ,选中点P、Q、R，构造圆上的弧QR,在弧上任选一点Ｔ,构造线段TP,标记角TP Ｒ。

《几何画板》与学生的数学实验在教学中，为了让学生获得知识，物理、化学、生物都需要实验，而在数学教学中，却没有实验。

自古以来，学生的数学知识都是依靠教师口头讲授获得的。

于是教师在“做”数学，而学生在被动地“听”数学。

他们听来的多半是缺少发现过程的结论，而且缺乏对老师所讲内容的“操作”。

数学不是教会的，学生必须经过自己的头脑想象和理解，才能学会，否则只是死记硬背罢了。

而那些相对于他们来说复杂而又抽象的图形，尤其需要学生自己去反复观察、探索、发现——建立学生自己的经验体系，然后在教师和书本的帮助下经过证明——建立学生自己的经验体系，最后在教师和书本的帮助下经过证明——建立学生自己的逻辑思维体系。

在以往的教学中，往往过分地强调了最后一步——结论的证明，这就大大脱离了学生的经验体系，致使不能很好地理解几何知识和几何逻辑。

《几何画板》正是理想的能够帮助学生从动态中观察、探索、发现的工具。

一实验开始，我们利用一个月近12课时的时间，对学生进行了WindowsXP 和《几何画板》的基础操作培训。

实验的过程中，我们首先为学生设计好课件制作的思路，也就是设计好教学情景，然后组织学生实验、交流。

为学生提供一种经验背景，让学生通过计算机从“听”数学转变到“做”数学，即以研究者的方式参与包括发现、探索在内的获得知识的全过程。

比如，在倾斜角与斜率的变化关系一节中，我们指导学生制作了课件，通过课件制作学生很直观地观察到了倾斜角与斜率的变化关系，课后学生也写出了很深刻的感受。

在实验的过程中，我们还对学生进行了“利用《几何画板》制作课件探讨解题思路的测试”。

二《几何画板》这个软件最大的特点是形象和动态。

而语言恰恰就是抽象的，一抽象了就不好懂，它提供的不是经验背景，而是提供的是语言、概念，是逻辑。

成年人因有了经验的支撑，有这个背景觉得讲得很清楚，而如果学生没有这种背景他就不可能懂。

关键是我们怎样给学生创造这些背景。

以往我们所提倡的直观教学就是想找到一种经验背景来帮助学生理解，但有时是找不到的。