随机振动加速度值及其功率谱密度的计量研究

Random Vibration1. 定义1.1 功率谱密度当波的频谱密度乘以一个适当的系数后将得到每单位频率波携带的功率，这被称为信号的功率谱密度（power spectral density, PSD）。

功率谱密度谱是一种概率统计方法，是对随机变量均方值的量度。

1.2 均方根均方根（RMS）是指将N项的平方和除于N后，开平方的结果。

均方根值也是有效值，如对于220交流电，示波器显示的有效值或均方根值为220V。

2. 加速度功率谱密度2.1 单位加速度单位：m/s^2或g加速度功率谱密度单位：（m/s^2）^2/Hz或g^2/HzHz单位为:1/s,所以加速度功率谱密度单位也可写为：m^2/s^32.2功率谱密度函数功率谱密度函数曲线的纵坐标是（g²/Hz）。

功率谱曲线下的面积就是随机加速度的总方差（g²）:σ²= ∫Φ（f）df其中：Φ（f）........功率谱密度函数σ ............. 均方根加速度3. 计算示例随机振动100-2000HZ，功率谱密度为0.01g^2/Hz，则其加速度峰值计算如下:σ²=0.01*(2000-100)=19σ=4.36g峰值加速度不大于3倍均方根加速度：13.08g4、SAE J 1455 随机振动要求4.1功率谱图4.1.1 Vertical axis4.1.2 Transverse axis4.1.3 Longitudinal axis4.2 Vertical axis加速度计算功率谱曲线下的面积：σ²=（40-5）0.016+0.5*（500-40）*0.016=4.24σ=2.06g峰值加速度不大于3倍均方根加速度：6.18g5. FGE随机振动要求5.1功率谱图5.2 要求在工作状态，振动频率范围：10Hz-1000Hz,振动方向：X、Y、Z三轴，试验时间：每轴各8h，加速度均方根为33.9 m/s²(3.46g)。

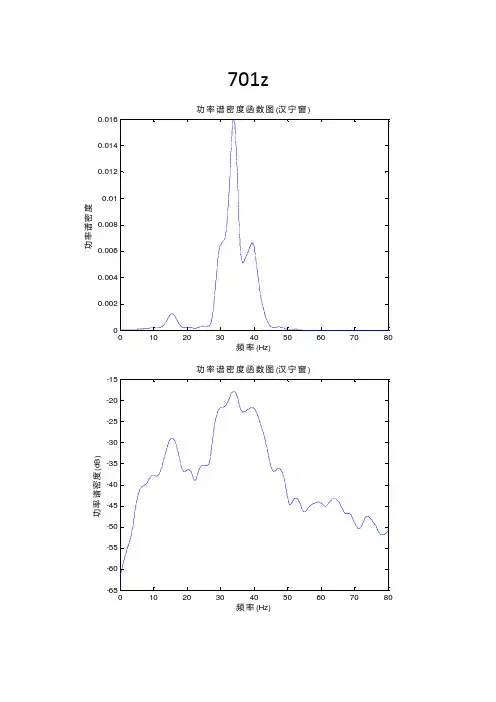
701z010203040506070800.0020.0040.0060.0080.010.0120.0140.016频率(Hz)功率谱密度功率谱密度函数图(汉宁窗)1020304050607080-65-60-55-50-45-40-35-30-25-20-15频率(Hz)功率谱密度(d B )功率谱密度函数图(汉宁窗)经过matlab 频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.1378m/s2(70km/h,z 方向，第一次试验，前排)0.1378010203040506070800.511.522.5-3频率(Hz)功率谱密度频率加权后功率谱密度函数图(汉宁窗)701y010203040506070801234567-3频率(Hz)功率谱密度功率谱密度函数图(汉宁窗)1020304050607080-70-65-60-55-50-45-40-35-30-25-20频率(Hz)功率谱密度(d B )功率谱密度函数图(汉宁窗)经过matlab 频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0164m/s2(70km/h,y 方向，第一次试验，前排)010203040506070800.511.522.53-5频率(Hz)功率谱密度频率加权后功率谱密度函数图(汉宁窗)701x010203040506070800.20.40.60.811.21.41.61.8-3频率(Hz)功率谱密度功率谱密度函数图(汉宁窗)01020304050607080-70-65-60-55-50-45-40-35-30-25频率(Hz)功率谱密度(d B )功率谱密度函数图(汉宁窗)经过matlab 频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0070m/s2(70km/h,x 方向，第一次试验，前排)010203040506070800.511.522.533.5-6频率(Hz)功率谱密度频率加权后功率谱密度函数图(汉宁窗)702经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0078m/s2(70km/h,x方向，第2次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0193m/s2(70km/h,y方向，第2次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.1393m/s2(70km/h,z方向，第2次试验，前排)703经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0035m/s2(70km/h,x方向，第1次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0038m/s2(70km/h,y方向，第1次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.027m/s2(70km/h,z方向，第1次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0052m/s2(70km/h,x方向，第2次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0072m/s2(70km/h,y方向，第2次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0296m/s2(70km/h,z方向，第2次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0062m/s2(60km/h,x方向，第1次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0144m/s2(60km/h,y方向，第1次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.1216m/s2(60km/h,z方向，第1次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0079m/s2(60km/h,x方向，第2次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0174m/s2(60km/h,y方向，第2次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.1172m/s2(60km/h,z方向，第2次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0032m/s2(60km/h,x方向，第1次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0063m/s2(60km/h,y方向，第1次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0267m/s2(60km/h,z方向，第1次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0029m/s2(60km/h,x方向，第2次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0058m/s2(60km/h,y方向，第2次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0231m/s2(60km/h,z方向，第2次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0058m/s2(50km/h,x方向，第1次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0170m/s2(50km/h,y方向，第1次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.1186m/s2(50km/h,z方向，第1次试验，前排)502（可疑数据）经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0122m/s2(50km/h,x方向，第2次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0302m/s2(50km/h,y方向，第2次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.1820m/s2(50km/h,z方向，第2次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0030m/s2(50km/h,x方向，第1次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0049m/s2(50km/h,y方向，第1次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0220m/s2(50km/h,z方向，第1次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0025m/s2(50km/h,x方向，第2次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0042m/s2(50km/h,y方向，第2次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0214m/s2(50km/h,z方向，第2次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0081m/s2(40km/h,x方向，第1次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0102m/s2(40km/h,y方向，第1次试验，前排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.1141m/s2(40km/h,z方向，第1次试验，前排)402（可疑数据）经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0092m/s2(40km/h,x方向，第2次试验，前排) 最大值=0.0468比值=5.2011<9经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0088m/s2(40km/h,y方向，第2次试验，前排) 最大值=0.0489比值=5.4457<9经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.1254m/s2(40km/h,z方向，第2次试验，前排)403经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0029m/s2(40km/h,x方向，第1次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0045m/s2(40km/h,y方向，第1次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0182m/s2(40km/h,z方向，第1次试验，后排)404经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0020m/s2(40km/h,x方向，第2次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0031m/s2(40km/h,y方向，第2次试验，后排)经过matlab频率加权法，利用功率谱密度函数计算得到加权加速度均方根值0.0162m/s2(40km/h,z方向，第2次试验，后排)。

第7章功率谱密度函数7.1 自相关的物理意义及其傅里叶变换7.2 自功率谱密度函数及其性质7.3 窄带随机过程与宽带随机过程7.4 互功率谱密度函数及其性质7.5 共相谱、正交谱和相干函数7.1 自相关的物理意义及其傅里叶变换自相关函数的物理意义可以表达现在的波形与时间坐标平移后的波形之间的相似程度表达随机过程两个不同截口处的两个随机变量之间的相关程度自相关函数与原始信号具有相同的周期（频率）、衰减率（阻尼）动态特性可用来检测随机过程中是否含有周期成分，或者其信号特征自功率谱计算的依据自相关函数既包含了一个随机过程间隔时间的相关程度和依赖性，同时也包含了能量大小的信息。

不过要注意，相关性再也不是象相关系数那样能够用-1到1这样的数来表示相关大小了自相关函数的性质1：⑴自相关函数是偶函数x x R E X t X t E X t X t R自相关函数的性质2：⑵周期平稳过程的自相关函数也是周期函数，其周期与过程的周期相同。

x x R T E X t X t T E X t X t R自相关函数的性质3：⑶τ=0时的自相关函数就是均方值20x x xR E X t X t R E X t X t⑷如果随机过程不是周期过程，则：22222222 01000x x xxx x xxx xxxx x C R R R R时，随机变量与它自身是完全相关的时，两个随机变量之间将不再相关前提：不是周期函数若，则 2lim x xR自相关函数的性质4：⑸自相关函数是一个有界函数22222 110xxx x xxxR R一般τ越大，则两时刻的随机变量X(t1)和X(t1+τ)之间的相关性愈差。

τ↑，Rx(τ)↓。

自相关函数的性质5：一、自功率谱密度函数二、互功率谱密度函数自相关函数Rx(τ)描述“平均功率”随时差τ的变化→“平均功率”的时间结构。

功率谱密度S x (f)：描述“平均功率”在频域（谱域）的分布→频率结构。

随机振动功率谱密度1.引言随机振动是一种常见的自然现象，具有广泛的应用背景。

在工程领域，随机振动现象普遍存在于各种结构物、机械系统和电子设备中。

为了理解和预测这些现象，需要采用有效的分析方法。

功率谱密度是描述随机振动特性的重要参数，对于研究随机振动具有重要意义。

本文将介绍随机振动功率谱密度的基本概念、理论、分析方法和应用。

1.1 随机振动概述随机振动是指一个或多个激励以非确定性方式作用在系统上，使得系统产生的响应具有统计性质。

随机振动的特点是具有时域和频域两个特征。

在时域中，随机振动表现为复杂的波动形式；在频域中，随机振动表现为能量的分布。

1.2 功率谱密度定义功率谱密度是描述随机振动能量在频率域上的分布。

它表示单位带宽内的能量，通常以分贝为单位表示。

功率谱密度是随机振动分析的重要工具，可以用于预测系统的响应和稳定性。

2.随机振动功率谱密度理论2.1 功率谱密度计算方法功率谱密度的计算方法主要有傅里叶变换和相关函数法。

傅里叶变换法是将时域信号通过傅里叶变换得到频域信号，从而计算功率谱密度。

相关函数法是通过测量两个时间点上的信号强度，并计算它们之间的相关函数，从而得到功率谱密度。

2.2 功率谱密度特性功率谱密度具有以下特性：(1) 功率谱密度是频率的函数，反映了随机振动在不同频率上的能量分布；(2) 功率谱密度具有归一化性质，即在整个频率范围内的积分等于1；(3) 对于稳态随机振动，功率谱密度是时间的函数，但在长期平均下，功率谱密度是恒定的；(4) 对于线性系统，功率谱密度与系统的阻尼比和自然频率有关。

3.随机振动功率谱密度分析3.1 频谱分析频谱分析是通过测量信号在不同频率上的振幅，从而得到功率谱密度的方法。

频谱分析可以用于研究随机振动的频率特性和能量分布。

通过分析频谱，可以了解系统在不同频率下的响应和稳定性。

3.2 时域分析时域分析是通过测量信号在不同时间点上的强度，从而得到功率谱密度的方法。

Alex-dreamer制作PSD：（可以相互传阅学习，但是鄙视那些拿着别人成果随意买卖！）PSD随机振动应用领域很广，比如雷达天线，飞机，桥梁，天平，地面，等等行业。

虽然现在对这方面公开资料很少，但是我相信以后会越来越多，发展的越来越成熟。

学术的浪潮总体是向前的，不会因为几个大牛保密自己的成果就会阻止我们对PSD研究，因此结合我的经验和爱好，我研究了一下两种PSD加载分析。

我标价的原则是含金量大小和花费我的时间以及我的经验值，如果你觉得值，就买；不值就不要下了。

因为我始终认为：士为知己者死，女为悦己者容。

算是互相尊重。

如果你得到这份资料，那就祝你好运！Good luck!-Alex-dreamer(南理工)一：目的：根据abaqus爱好者提出的PSD随机振动分析，提出功率谱如何定义及如何加载？如果功率谱是加速度的平方，如何加载？如果在输入点施加载荷功率谱如何定义？本文将给出详细的分析过程。

二：随机振动基本概念1. 随机振动的输入量和输出量都是概率统计值，因此存在不确定性。

输入量为PSD （功率谱密度）曲线，分为加速度、速度、位移或者力的PSD曲线；最常见的是加速度PSD，常用语BASE MOTION基础约束加载。

2. 随机振动的响应符合正态分布，PSD实际上是随机变量的能量分布，也就是在不同频率上的方差值，反映不同频率处的振动能量，PSD曲线所围成的面积是随机变量总响应的方差值；3. RMS为随机变量的标准方差，将PSD曲线包络面积开平方即为RMS。

4. 随机振动输出的位移、应力、应变等值都是对应不同频率的方差值（即PSD值），量纲为x^2，当然也可以输出这些变量的均方根值（即RMS值）；abaqus6.10以上版本可以直接在场变量里面输出设置。

见下文。

5. 如果是单个激励源，定义为非相关性分析，如是多个激励源，则需要定义相关性参数。

因此出现type=uncorrelated。

三：模型简介：1）该模型很简单，是hypermesh中一个双孔模型。

随机过程的功率谱密度随机过程是一种具有随机变量的序列，其性质随时间变化。

功率谱密度是用来描述随机过程频谱特性的一种工具。

本文将介绍随机过程的基本概念，探讨功率谱密度的定义和计算方法，并讨论其在实际应用中的意义。

一、随机过程的基本概念随机过程是一种随时间变化的随机变量序列。

在随机过程中，每个时间点上的变量都是随机的，可以用数学统计的方法进行描述与分析。

随机过程常用于模拟与分析具有随机性的现象，如通信信号、股票价格等。

二、功率谱密度的定义功率谱密度是描述随机过程频谱特性的一种工具，用于表示随机过程在不同频率上的分布情况。

功率谱密度函数通常用符号S(f)表示，其中f为频率。

三、功率谱密度的计算方法计算功率谱密度可以使用多种方法，常见的有周期图法、自相关函数法和傅里叶变换法等。

下面分别介绍这些方法的基本原理：1. 周期图法周期图法是一种直观的计算功率谱密度的方法。

它通过对随机过程的重复实现进行频率分析，得到信号的谱图。

周期图法的实现过程包括样本采集、周期图的构建和谱估计等步骤。

2. 自相关函数法自相关函数法是一种基于信号的自相关函数计算功率谱密度的方法。

它通过计算随机过程与其自身在不同时间点上的相关性，得到功率谱密度函数。

自相关函数法的实现过程包括自相关函数的计算和功率谱密度的估计等步骤。

3. 傅里叶变换法傅里叶变换法是一种基于信号的傅里叶变换计算功率谱密度的方法。

它通过将时域信号转换到频域，得到信号的频谱分布。

傅里叶变换法的实现过程包括信号的傅里叶变换和功率谱密度的计算等步骤。

四、功率谱密度的实际应用功率谱密度在信号处理、通信系统设计、噪声分析等领域都有重要应用。

以下是一些典型的实际应用场景：1. 信号处理功率谱密度可以用于对信号进行频谱分析和滤波器设计。

通过分析信号的功率谱密度，可以了解信号的频率分布情况，并根据需求设计相应的滤波器，实现信号的去噪、增强等处理。

2. 通信系统设计功率谱密度可以用于对通信系统中的噪声进行分析和优化。

**workbench随机振动功率谱密度转换及均方根加速度计算**随机振动在工程领域中有着广泛的应用，而对于工作台（workbench）的随机振动功率谱密度转换及均方根加速度计算，是进行振动分析和评估的重要步骤。

本文将按照从简到繁的方式，深入探讨workbench 随机振动功率谱密度转换及均方根加速度计算的过程和原理，帮助您全面理解和掌握这一技术。

一、工作台（workbench）随机振动功率谱密度转换1. 什么是随机振动功率谱密度？随机振动功率谱密度是描述随机振动信号的频率内容和能量分布特性的一种方法。

在工程中，通常使用功率谱密度来描述结构在振动过程中的能量分布情况，它反映了结构在不同频率下的振动能量大小。

2. 工作台（workbench）随机振动功率谱密度转换的步骤：- 数据采集：首先需要对工作台进行振动信号数据的采集，一般采用加速度传感器等装置来获取振动信号。

- 信号预处理：对采集到的振动信号进行预处理，包括去噪、滤波等操作，以确保信号的准确性和可靠性。

- 功率谱密度计算：利用相应的算法和工具对预处理后的振动信号进行功率谱密度的计算，得到频率内容和能量分布情况。

- 结果分析：对计算得到的功率谱密度进行分析和解释，以评估工作台在不同频率下的振动情况。

二、工作台（workbench）均方根加速度计算1. 什么是均方根加速度？均方根加速度是描述振动信号幅值大小的重要参数之一，它可以反映结构在振动过程中的瞬时加速度幅值。

在工程评估和设计中，常常使用均方根加速度来分析和评估结构的振动特性。

2. 工作台（workbench）均方根加速度计算的方法：- 振动信号采集：同样需要对工作台进行振动信号数据的采集，通常使用加速度传感器等装置来获取振动信号。

- 信号处理：对采集到的振动信号进行处理，包括去除直流分量、噪声滤波等操作，以得到准确的振动信号。

- 均方根加速度计算：利用相应的算法和工具对处理后的振动信号进行均方根加速度的计算，得到结构在振动过程中的瞬时加速度幅值大小。

随机振动加速度估值公式
随机振动加速度估值公式是描述振动加速度的数学表达式，用于计算物体在随机振动过程中的加速度变化。

这个公式在工程领域中广泛应用，特别是在振动控制和结构动力学方面。

它可以帮助工程师们更好地理解和预测振动的特性，以便设计出更安全和稳定的结构。

随机振动加速度估值公式可以分为两个部分：一是描述振动源的特性，二是计算振动传递路径上的加速度。

对于振动源的特性，通常可以使用功率谱密度函数来描述。

这个函数反映了振动信号在不同频率上的能量分布情况。

通过对振动源的功率谱密度函数进行傅里叶变换，可以得到振动信号的频域表达式。

在计算振动传递路径上的加速度时，可以使用传递函数来描述振动信号在不同频率上的传递特性。

传递函数是振动信号在结构中传递的过程中发生的变化关系，可以用来计算振动信号从振动源到接收点的传递函数值。

通过将振动源的功率谱密度函数与传递函数相乘，可以得到传递路径上的振动加速度的估值。

需要注意的是，随机振动加速度估值公式只是对振动加速度的一种估计，实际情况可能存在误差。

因此，在实际工程中，需要根据具体情况进行实测和分析，以得到更准确的振动加速度数值。

随机振动加速度估值公式是工程领域中用于计算振动加速度的数学表达式。

它可以帮助工程师们更好地理解和预测振动的特性，以便
设计出更安全和稳定的结构。

但需要注意的是，公式只是对振动加速度的一种估计，实际情况可能存在误差，因此需要根据具体情况进行实测和分析。

通过合理应用这个公式，可以提高工程结构的振动控制和设计质量，保障人们的生命财产安全。

随机信号的功率谱密度估计方法研究【摘要】对确定性信号进行傅里叶变换是在频率域分析研究的理论基础，但对于随机信号来说，其傅里叶变换并不存在，因此转型研究它的功率谱。

这样就可以用功率谱来描述随机信号的频域特性。

功率谱是功率谱密度的简称，是自相关函数的傅里叶变换。

随机信号的功率谱密度用来描述信号的能量特征随频率的变化关系。

对功率谱密度的估计又称功率谱估计。

功率谱估计是数字信号处理中的一个重要组成部分，其理论研究已经非常成熟，但是传统的仿真实现由于计算量的庞大而往往令人望而却步。

采用功能强大的MA TLAB软件对功率谱估计进行仿真，便于深刻理解各种方法的特点，从而在实际工作中做出合理的选择。

本文简要介绍了MA TLAB仿真软件的基本功能、特点和优势，然后具体介绍了周期图法。

【关键词】自相关函数;功率谱;MA TLAB;随机信号; 周期图法.Random signal power spectral density estimationmethod researchAbstract:Fourier transform of the deterministic signals is the theoretical foundation of the frequency domain analysis, but for random signal, its Fourier transform does not exist, so we change to study the power spectrum. So it can be used to describe the random power spectrum of the signal frequency characteristics 。

Power spectrum is the power spectral density abbreviation, is the autocorrelation function of Fourier transformation 。

加速度频谱密度计算加速度頻譜密度的计算加速度頻譜密度(Acceleration Spectral Density, ASD)就是隨機振動的功率頻譜密度(Power Spectral Density, PSD)，就如同dazz所說。

隨機振動只能用能量表示，單位為g^2(加速度g平方)，密度是指單位頻寬。

取窄頻帶振動時域訊號的傅立葉轉換值平方後除以頻帶寬，即可計算得到該頻帶對應的加速度頻譜密度值。

振动力学公式供大家参考1、求推力（F）的公式F=（m0+m1+m2+ ……）A…………………………公式（1）式中：F—推力（激振力）（N）m0—振动台运动部分有效质量（kg）m1—辅助台面质量（kg）m2—试件（包括夹具、安装螺钉）质量（kg）A—试验加速度（m/s2）2、加速度（A）、速度（V）、位移（D）三个振动参数的互换运算公式2.1 A=ωv ……………………………………………………公式（2）式中：A—试验加速度（m/s2）V—试验速度（m/s）ω=2πf（角速度）其中f为试验频率（Hz）2.2 V=ωD×10-3 ………………………………………………公式（3）式中：V和ω与“2.1”中同义D—位移（mm0-p）单峰值2.3 A=ω2D×10-3 ………………………………………………公式（4）式中：A、D和ω与“2.1”，“2.2”中同义公式（4）亦可简化为：A=式中：A和D与“2.3”中同义，但A的单位为g1g=9.8m/s2所以：A≈ ,这时A的单位为m/s2定振级扫频试验平滑交越点频率的计算公式3.1 加速度与速度平滑交越点频率的计算公式fA-V= ………………………………………公式（5）式中：fA-V—加速度与速度平滑交越点频率（Hz）（A和V与前面同义）。

3.2 速度与位移平滑交越点频率的计算公式…………………………………公式（6）式中：—加速度与速度平滑交越点频率（Hz）（V和D与前面同义）。

加速度頻譜密度的计算加速度頻譜密度(Acceleration Spectral Density, ASD)就是隨機振動的功率頻譜密度(Power Spectral Density, PSD),就如同dazz所說。

隨機振動只能用能量表示,單位為g^2(加速度g平方),密度是指單位頻寬。

取窄頻帶振動時域訊號的傅立葉轉換值平方後除以頻帶寬,即可計算得到該頻帶對應的加速度頻譜密度值。

振动力学公式供大家参考1、求推力(F)的公式F=(m0+m1+m2+ ……)A…………………………公式(1)式中:F—推力(激振力)(N)m0—振动台运动部分有效质量(kg)m1—辅助台面质量(kg)m2—试件(包括夹具、安装螺钉)质量(kg)A—试验加速度(m/s2)2、加速度(A)、速度(V)、位移(D)三个振动参数的互换运算公式2.1 A=ωv ……………………………………………………公式(2)式中:A—试验加速度(m/s2)V—试验速度(m/s)ω=2πf(角速度)其中f为试验频率(Hz)2.2 V=ωD×10-3 ………………………………………………公式(3) 式中:V和ω与“2.1”中同义D—位移(mm0-p)单峰值2.3 A=ω2D×10-3 ………………………………………………公式(4) 式中:A、D和ω与“2.1”,“2.2”中同义公式(4)亦可简化为:A=式中:A和D与“2.3”中同义,但A的单位为g1g=9.8m/s2所以:A≈ ,这时A的单位为m/s2定振级扫频试验平滑交越点频率的计算公式3.1 加速度与速度平滑交越点频率的计算公式fA-V= ………………………………………公式(5)式中:fA-V—加速度与速度平滑交越点频率(Hz)(A和V与前面同义)。

3.2 速度与位移平滑交越点频率的计算公式…………………………………公式(6)式中:—加速度与速度平滑交越点频率(Hz)(V和D与前面同义)。

加速度頻譜密度的计算加速度頻譜密度(Acceleration Spectral Density, ASD)就是隨機振動的功率頻譜密度(Power Spectral Density, PSD),就如同dazz所說。

隨機振動只能用能量表示,單位為g^2(加速度g平方),密度是指單位頻寬。

取窄頻帶振動時域訊號的傅立葉轉換值平方後除以頻帶寬,即可計算得到該頻帶對應的加速度頻譜密度值。

振动力学公式供大家参考1、求推力(F)的公式F=(m0+m1+m2+ ……)A…………………………公式(1)式中:F—推力(激振力)(N)m0—振动台运动部分有效质量(kg)m1—辅助台面质量(kg)m2—试件(包括夹具、安装螺钉)质量(kg)A—试验加速度(m/s2)2、加速度(A)、速度(V)、位移(D)三个振动参数的互换运算公式2.1 A=ωv ……………………………………………………公式(2)式中:A—试验加速度(m/s2)V—试验速度(m/s)ω=2πf(角速度)其中f为试验频率(Hz)2.2 V=ωD×10-3 ………………………………………………公式(3) 式中:V和ω与“2.1”中同义D—位移(mm0-p)单峰值2.3 A=ω2D×10-3 ………………………………………………公式(4) 式中:A、D和ω与“2.1”,“2.2”中同义公式(4)亦可简化为:A=式中:A和D与“2.3”中同义,但A的单位为g1g=9.8m/s2所以:A≈ ,这时A的单位为m/s2定振级扫频试验平滑交越点频率的计算公式3.1 加速度与速度平滑交越点频率的计算公式fA-V= ………………………………………公式(5)式中:fA-V—加速度与速度平滑交越点频率(Hz)(A和V与前面同义)。

3.2 速度与位移平滑交越点频率的计算公式…………………………………公式(6)式中:—加速度与速度平滑交越点频率(Hz)(V和D与前面同义)。

加速度頻譜密度的计算加速度頻譜密度(Acceleration Spectral Density, ASD)就是隨機振動的功率頻譜密度(Power Spectral Density, PSD),就如同dazz所說。

隨機振動只能用能量表示,單位為g^2(加速度g平方),密度是指單位頻寬。

取窄頻帶振動時域訊號的傅立葉轉換值平方後除以頻帶寬,即可計算得到該頻帶對應的加速度頻譜密度值。

振动力学公式供大家参考1、求推力(F)的公式F=(m0+m1+m2+ ……)A…………………………公式(1)式中:F—推力(激振力)(N)m0—振动台运动部分有效质量(kg)m1—辅助台面质量(kg)m2—试件(包括夹具、安装螺钉)质量(kg)A—试验加速度(m/s2)2、加速度(A)、速度(V)、位移(D)三个振动参数的互换运算公式2.1 A=ωv ……………………………………………………公式(2)式中:A—试验加速度(m/s2)V—试验速度(m/s)ω=2πf(角速度)其中f为试验频率(Hz)2.2 V=ωD×10-3 ………………………………………………公式(3) 式中:V和ω与“2.1”中同义D—位移(mm0-p)单峰值2.3 A=ω2D×10-3 ………………………………………………公式(4) 式中:A、D和ω与“2.1”,“2.2”中同义公式(4)亦可简化为:A=式中:A和D与“2.3”中同义,但A的单位为g1g=9.8m/s2所以:A≈ ,这时A的单位为m/s2定振级扫频试验平滑交越点频率的计算公式3.1 加速度与速度平滑交越点频率的计算公式fA-V= ………………………………………公式(5)式中:fA-V—加速度与速度平滑交越点频率(Hz)(A和V与前面同义)。

3.2 速度与位移平滑交越点频率的计算公式…………………………………公式(6)式中:—加速度与速度平滑交越点频率(Hz)(V和D与前面同义)。