随机振动功率谱密度

Random Vibration1. 定义1.1 功率谱密度当波的频谱密度乘以一个适当的系数后将得到每单位频率波携带的功率，这被称为信号的功率谱密度（power spectral density, PSD）。

功率谱密度谱是一种概率统计方法，是对随机变量均方值的量度。

1.2 均方根均方根（RMS）是指将N项的平方和除于N后，开平方的结果。

均方根值也是有效值，如对于220交流电，示波器显示的有效值或均方根值为220V。

2. 加速度功率谱密度2.1 单位加速度单位：m/s^2或g加速度功率谱密度单位：（m/s^2）^2/Hz或g^2/HzHz单位为:1/s,所以加速度功率谱密度单位也可写为：m^2/s^32.2功率谱密度函数功率谱密度函数曲线的纵坐标是（g²/Hz）。

功率谱曲线下的面积就是随机加速度的总方差（g²）:σ²= ∫Φ（f）df其中：Φ（f）........功率谱密度函数σ ............. 均方根加速度3. 计算示例随机振动100-2000HZ，功率谱密度为0.01g^2/Hz，则其加速度峰值计算如下:σ²=0.01*(2000-100)=19σ=4.36g峰值加速度不大于3倍均方根加速度：13.08g4、SAE J 1455 随机振动要求4.1功率谱图4.1.1 Vertical axis4.1.2 Transverse axis4.1.3 Longitudinal axis4.2 Vertical axis加速度计算功率谱曲线下的面积：σ²=（40-5）0.016+0.5*（500-40）*0.016=4.24σ=2.06g峰值加速度不大于3倍均方根加速度：6.18g5. FGE随机振动要求5.1功率谱图5.2 要求在工作状态，振动频率范围：10Hz-1000Hz,振动方向：X、Y、Z三轴，试验时间：每轴各8h，加速度均方根为33.9 m/s²(3.46g)。

通信原理第七版功率谱密度计算公式功率谱密度（=power spectral/spectrum density）
计算方法有多种。

第一种是维纳辛钦定理(a.k.a Wiener-Khinchin theorem)，要求是广义平稳的随机过程，其功率谱密度和自相关函数是一对傅里叶变换。

离散写法类似。

第二种是帕斯瓦尔定理(Parseval's theorem)
其功率谱密度为一般实信号在时域频域积分的积分和自相关函数在=0的时候值是一样的，这个是常用性质之一。

功率谱密度计算公式：p=(g2/Hz)。

在物理学中，信号通常是波的形式表示，例如电磁波、随机振动或者声波。

当波的功率频谱密度乘以一个适当的系数后将得到每单位频率波携带的功率，这被称为信号的功率谱密度。

物理学是研究物质运动最一般规律和物质基本结构的学科。

作为自然科学的带头学科，物理学研究大至宇宙，小至基本粒子等一切物质最基本的运动形式和规律，因此成为其他各自然科学学科的研究基础。

物理学的理论结构充分地运用数学作为自己的工作语言，以实验作为检验理论正确性的唯一标准，它是当今最精密的一门自然科学学科。

功率谱密度谱是一种概率统计方法，是对随机变量均方值的量度。

一般用于随机振动分析，连续瞬态响应只能通过概率分布函数进行描述，即出现某水平响应所对应的概率。

功率谱密度是结构在随机动态载荷激励下响应的统计结果，是一条功率谱密度值—频率值的关系曲线，其中功率谱密度可以是位移功率谱密度、速度功率谱密度、加速度功率谱密度、力功率谱密度等形式。

数学上，功率谱密度值—频率值的关系曲线下的面积就是方差，即响应标准偏差的平方值。

谱是个很不严格的东西，常常指信号的Fourier变换，是一个时间平均（time average）概念功率谱的概念是针对功率有限信号的(能量有限信号可用能量谱分析)，所表现的是单位频带内信号功率随频率的变换情况。

保留频谱的幅度信息，但是丢掉了相位信息，所以频谱不同的信号其功率谱是可能相同的。

有两个重要区别：1。

功率谱是随机过程的统计平均概念，平稳随机过程的功率谱是一个确定函数；而频谱是随机过程样本的Fourier变换，对于一个随机过程而言，频谱也是一个“随机过程”。

（随机的频域序列）2。

功率概念和幅度概念的差别。

此外，只能对宽平稳的各态历经的二阶矩过程谈功率谱，其存在性取决于二阶局是否存在并且二阶矩的Fourier变换收敛；而频谱的存在性仅仅取决于该随机过程的该样本的Fourier变换是否收敛。

热心网友回答提问者对于答案的评价：谢谢解答。

频谱分析（也称频率分析），是对动态信号在频率域内进行分析，分析的结果是以频率为坐标的各种物理量的谱线和曲线，可得到各种幅值以频率为变量的频谱函数F(ω)。

频谱分析中可求得幅值谱、相位谱、功率谱和各种谱密度等等。

频谱分析过程较为复杂，它是以傅里叶级数和傅里叶积分为基础的。

功率谱是个什么概念？它有单位吗?随机信号是时域无限信号，不具备可积分条件，因此不能直接进行傅氏变换。

一般用具有统计特性的功率谱来作为谱分析的依据。

功率谱与自相关函数是一个傅氏变换对。

功率谱具有单位频率的平均功率量纲。

随机振动功率谱密度1.引言随机振动是一种常见的自然现象，具有广泛的应用背景。

在工程领域，随机振动现象普遍存在于各种结构物、机械系统和电子设备中。

为了理解和预测这些现象，需要采用有效的分析方法。

功率谱密度是描述随机振动特性的重要参数，对于研究随机振动具有重要意义。

本文将介绍随机振动功率谱密度的基本概念、理论、分析方法和应用。

1.1 随机振动概述随机振动是指一个或多个激励以非确定性方式作用在系统上，使得系统产生的响应具有统计性质。

随机振动的特点是具有时域和频域两个特征。

在时域中，随机振动表现为复杂的波动形式；在频域中，随机振动表现为能量的分布。

1.2 功率谱密度定义功率谱密度是描述随机振动能量在频率域上的分布。

它表示单位带宽内的能量，通常以分贝为单位表示。

功率谱密度是随机振动分析的重要工具，可以用于预测系统的响应和稳定性。

2.随机振动功率谱密度理论2.1 功率谱密度计算方法功率谱密度的计算方法主要有傅里叶变换和相关函数法。

傅里叶变换法是将时域信号通过傅里叶变换得到频域信号，从而计算功率谱密度。

相关函数法是通过测量两个时间点上的信号强度，并计算它们之间的相关函数，从而得到功率谱密度。

2.2 功率谱密度特性功率谱密度具有以下特性：(1) 功率谱密度是频率的函数，反映了随机振动在不同频率上的能量分布；(2) 功率谱密度具有归一化性质，即在整个频率范围内的积分等于1；(3) 对于稳态随机振动，功率谱密度是时间的函数，但在长期平均下，功率谱密度是恒定的；(4) 对于线性系统，功率谱密度与系统的阻尼比和自然频率有关。

3.随机振动功率谱密度分析3.1 频谱分析频谱分析是通过测量信号在不同频率上的振幅，从而得到功率谱密度的方法。

频谱分析可以用于研究随机振动的频率特性和能量分布。

通过分析频谱，可以了解系统在不同频率下的响应和稳定性。

3.2 时域分析时域分析是通过测量信号在不同时间点上的强度，从而得到功率谱密度的方法。

随机过程的谱密度与功率谱密度随机过程是在时间上随机变化的过程，它在许多领域中都有广泛的应用。

在研究随机过程时，谱密度和功率谱密度是两个重要的概念。

一、谱密度谱密度是描述随机过程在频域上的性质的一种测量，它用来表示随机过程的频谱特性。

谱密度通常用符号S(f)表示，其中f是频率。

谱密度是随机过程各频率成分的功率平均值，即将随机过程在不同频率上的功率加权平均得到的值。

谱密度越大，表示在该频率上的成分越强。

对于离散随机过程，谱密度可以通过对其自相关函数进行傅里叶变换得到。

而对于连续随机过程，谱密度可以通过对其自相关函数进行傅里叶变换或拉普拉斯变换得到。

谱密度具有一些重要的性质，例如：1. 谱密度是非负的且对称的。

2. 谱密度在频率上的积分等于随机过程的方差。

3. 谱密度函数是随机过程的一种特征，不同的谱密度函数可以表示不同的随机过程。

二、功率谱密度功率谱密度是描述随机过程在频域上能量分布的一种测量，也可以理解为随机过程的平均功率。

功率谱密度通常用符号S(f)表示，其中f 是频率。

与谱密度类似，功率谱密度也可以通过随机过程的自相关函数进行傅里叶变换或拉普拉斯变换得到。

功率谱密度表示随机过程各频率成分的功率分布，即在不同频率上的功率值。

功率谱密度越大，表示在该频率上的功率越强。

功率谱密度具有一些重要的性质，例如：1. 功率谱密度是非负的。

2. 功率谱密度在频率上的积分等于随机过程的总功率。

3. 功率谱密度函数是随机过程的一种特征，不同的功率谱密度函数可以表示不同的随机过程。

三、谱密度与功率谱密度的关系谱密度和功率谱密度之间存在一定的关系。

对于连续随机过程，谱密度和功率谱密度可以通过以下关系进行转换：S(f) = |H(f)|^2 * P(f)其中，S(f)表示谱密度，H(f)表示系统的频率响应函数，P(f)表示功率谱密度。

这个关系说明了谱密度和功率谱密度之间的链接，它们在频域上描述了随机过程的特性。

结论谱密度和功率谱密度是研究随机过程的重要工具，它们在频域上描述了随机过程的特性。

加速度頻譜密度(Acceleration Spectral Density, ASD)就是隨機振動的功率頻譜密度(Power Spectral Density, PSD)，隨機振動只能用能量表示，單位為g^2(加速度g平方)，密度是指單位頻寬。

取窄頻帶振動時域訊號的傅立葉轉換值平方後除以頻帶寬，即可計算得到該頻帶對應的加速度頻譜密度值。

ASD：加速度谱密度常用单位：(m/s2)2 /Hz，m2/s3PSD：功率谱密度常用单位：g2/Hz （一般是根据实测数据（一般是测加速度），简化处理得到振动台所需要的PSD，或是根据相关标准直接得到。

）加速度谱密度就是（功率谱密度）它是指每个单位频率的能量。

换算公式：1g2/Hz=96.04（m/s2)2 /Hz=96.04m2/s3g — 加速度(acceleration)的单位,每秒增加9.81公尺称为一个加速度.1 g = 9.81 m/s2lg2/Hz — 功率频谱密度(P.S.D)的单位,每单位时间内所做的功率.lG rms — 指将各频率点之功率频谱密度进行积分后的总能量,为有效值.我们平常所说的g‘值是一个重力加速度值，就是1G=9.8m/s2, 而Grms是个积累的物理量，类似于能量一样，在一定的频率范围内对PSD积分（近似的算法就是求面积，在将面积开方就是你所需要的了），然后将积分的结果开方，也叫加速度总均方根值。

在物理学中，信号通常是波的形式，例如电磁波、随机振动或者声波。

当波的频谱密度乘以一个适当的系数后将得到每单位频率波携带的功率，这被称为信号的功率谱密度（power spectral density, PSD）或者谱功率分布（spectral power distribution, SPD）。

功率谱密度的单位通常用每赫兹的瓦特数（W/Hz）表示，或者使用波长而不是频率，即每纳米的瓦特数（W/nm）来表示。

因为运动的质点处于不规则的运动状态，永远不会精确地重复，对其进行一系列的测量各次记录也不一样，所以没有固定的周期。

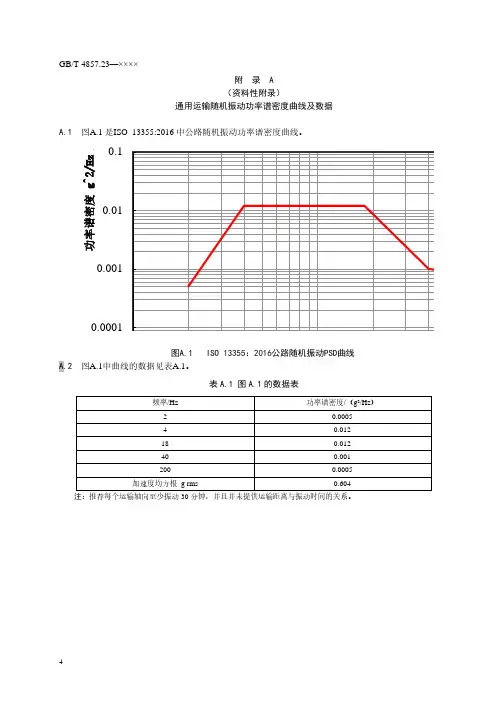
附 录 A（资料性附录）通用运输随机振动功率谱密度曲线及数据A.1 图A.1是ISO 13355:2016中公路随机振动功率谱密度曲线。

0.00010.0010.010.1功率谱密度g ^2/H zA.2 图A.1注：推荐每个运输轴向至少振动30分钟，并且并未提供运输距离与振动时间的关系。

附录 B（资料性附录）国际相关标准随机振动功率谱密度曲线及数据B.1ISTA 3A-2018车辆随机振动的功率谱密度曲线和数据。

B.1.1图B.1是ISTA 3A-2018车辆随机振动的功率谱密度曲线。

B.2 ASTM D4169-2016卡车随机振动的功率谱密度曲线和数据。

B.2.1 图B.2是ASTM D4169-2016卡车随机振动不同严酷水平的功率谱密度曲线。

附 录 C（资料性附录）中国公路运输和京沪铁路运输随机振动功率谱密度曲线及数据C.1 钢簧减振卡车在中国部分地区公路上不同运输方式的几种不同严酷水平的振动强度的功率谱密度曲线和数据。

C.1.1 图C.1是中国公路运输钢簧减震车的功率谱密度曲线。

0.00010.0010.010.1功率谱密度g ^2/H zC.1.2 图C.1注1：应根据产品的价值，预期能够承受危害的程度、货运单元的数量、运输环境的相关信息或其它准则确定试验强度严酷水平，严酷水平Ⅰ为强度最大，严酷水平Ⅲ为强度最小，严酷水平Ⅱ为一般水平，通常推荐严酷水平Ⅱ。

注2：运输距离不明的情况下，推荐试验时间为180分钟。

注3：如果已知包装件的运输总距离，也可按照以下经验公式推算试验时间；t=S/K式中：t——试验时间，单位为分钟（min）；S——运输总距离，单位为千米（km）；K——试验时间估算常数，K取6，单位为千米每分钟（km /min）。

C.2 采集的京沪铁路行李车实际垂直轴向振动数据的功率谱密度曲线和数据。

C.2.1图C.2京沪铁路行李车垂直轴向的功率谱密度曲线。