初二秋.第1讲.四点共圆(一)

四点共圆引言在几何学中，四点共圆是一个经典的概念，它指的是四个不在一条直线上的点可以构成同一个圆。

本文将介绍四点共圆的基本概念、性质以及证明方法。

基本概念四点共圆是指当给定四个不在一条直线上的点时，存在一个圆可以通过这四个点。

为了方便讨论，我们将这四个点依次标记为A、B、C和D，并假设它们不共线。

这样，我们可以通过构造圆来证明是否四点共圆。

性质根据四点共圆的定义，我们可以得出以下性质：•任意三个点确定一个圆，即如果取三个点A、B和C，那么存在一个圆可以通过这三个点。

•如果四个点A、B、C和D共圆，那么它们的任意三个点仍然共圆，即如果A、B、C和D共圆，那么A、B和C共圆，A、B和D共圆，以及B、C和D共圆等。

证明方法下面我们将介绍两种常见的证明方法，即推论法和向量法。

推论法推论法是一种常见的证明四点共圆的方法，它基于欧氏几何的公理和定理。

以下是一个简单的推论法证明：证明：设四个点A、B、C和D不共线。

为了证明它们共圆，我们需要证明存在一个圆可以通过这四个点。

首先，选择其中三个点A、B和C。

根据性质1，存在一个圆可以通过这三个点，假设这个圆为O1。

接下来，我们选择点D。

我们希望证明点D也在圆O1上。

为此，我们需要证明点D和圆O1的半径相等。

利用欧氏几何中的定理，我们可以证明从圆心到半径上任意一点的距离相等。

因此，我们只需要证明点D到圆心O1的距离与其他三个点到圆心O1的距离相等。

通过推理，我们可以得出结论：点D也在圆O1上。

因此，四个点A、B、C和D共圆。

向量法向量法是另一种常见的证明四点共圆的方法。

它基于向量的运算和性质。

以下是一个简单的向量法证明：证明：设四个点A、B、C和D不共线。

为了证明它们共圆，我们需要证明存在一个圆可以通过这四个点。

假设圆的圆心为O，我们需要证明向量OA、OB、OC和OD共面。

根据向量运算的性质，我们可以使用向量混合积来判断向量是否共面。

根据向量混合积的定义，我们有以下公式：(OA × OB) · (OC × OD) = (OA · OC) × (OB · OD) - (OA · OD) × (OB · OC)其中，× 表示向量的叉乘，·表示向量的点乘。

四点共圆四点共圆是一个几何学中的概念，指的是四个点在同一个圆上。

定义在平面几何中，给定四个不共线的点A、B、C和D，如果这四个点可以被一个圆围起来，使得这四个点都位于圆的周上，那么这四个点就被称为共圆点，同时被围住的圆称为这四个点共有的圆，也称为这四个点的外接圆。

特性四点共圆的特性如下：1.圆心定理：四个点共圆的圆心是这四个点连线的交点的中垂线相交处。

2.弦的性质：相交于圆弦上的两个弧被它们所包含的圆心角所对应的弧所等分。

3.弧度的性质：共圆的四个点所对应的弧所对应的弧度相等。

4.弧角的性质：共圆的四个点所对应的弧所对应的圆心角度相等。

判定判定四个点是否共圆有多种方法，下面介绍两种常用的判定方法：1.同样圆周角的测量方法：计算并对比四个可能的圆周角，如果它们的度数相等，则这四个点共圆。

2.使用外接圆标准方程判定：根据外接圆标准方程，计算四个点的坐标，并将它们带入方程来验证。

如果四个点坐标满足方程，则这四个点共圆。

应用四点共圆的概念在几何学中有广泛的应用，下面列举几个常见的应用：1.三角形外接圆：在一个三角形ABC中，如果三个顶点A、B、C共圆，则称这个圆为三角形ABC的外接圆。

外接圆在三角形的各个关系中有着重要的作用。

2.圆的切线：在切点的两侧，圆的切线与切点所对应的弧所对应圆心角的度数相等。

这个性质可以用于证明几何问题。

3.三点定圆：给定三个点，通过它们共圆的圆心和半径，可以确定一个唯一的圆。

这个性质被广泛应用于圆的构造和计算。

总结四点共圆是一个重要的几何学概念，它涉及到圆的构造和性质，具有一定的理论和实际应用价值。

通过学习四点共圆的定义、特性和判定方法，我们可以更好地理解和应用几何学中的相关知识。

我们要找出一个具体的例子，说明在初中数学中四点共圆的情况。

首先，我们要明白什么是四点共圆。

如果一个平面上四个点都在同一个圆上，那么这四个点就称为四点共圆。

为了找到一个具体的例子，我们可以考虑一个直角三角形。

直角三角形的斜边的中点、直角顶点和另一个锐角顶点是四点共圆的。

现在我们要来证明这个性质。

假设直角三角形为ΔABC，其中∠C=90°，D是斜边BC 的中点，E是顶点A。

第一步，连接AD和DE。

由于D是斜边BC的中点，根据中位线性质，我们知道AD 是BC的一半，即AD=BD=CD。

第二步，由于D是BC的中点，所以∠BAD = ∠CAD。

第三步，根据等腰三角形的性质，在等腰三角形中，底边的两个角是相等的。

所以，∠ADE = ∠BDE。

第四步，由于∠BAC + ∠CAD = 90°且∠ACB + ∠BCD = 90°，
所以∠BAC = ∠BCD。

结合第三步的结果，我们可以得出：∠BAC = ∠ADE = ∠BDE = ∠ACD。

第五步，根据角的和性质，如果两个角的和是180°，那么这两个角是互补的。

由于∠BAC + ∠ACD = 180°，所以四点A、D、B、E共圆。

综上所述，我们证明了在直角三角形中，斜边的中点、直角顶点和另一个锐角顶点是四点共圆的。

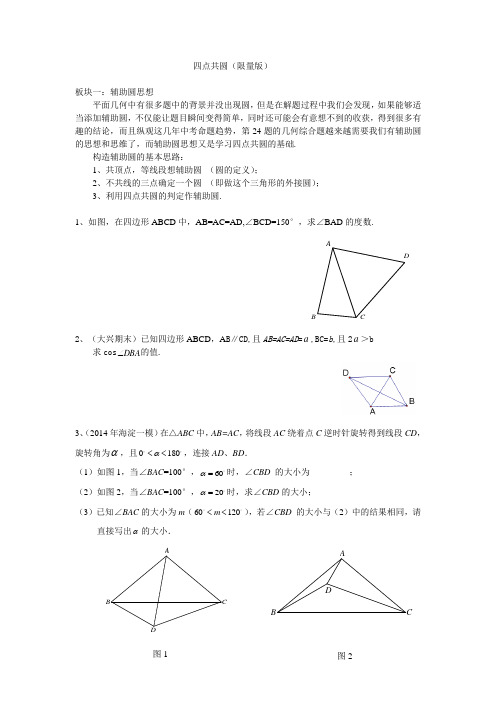
四点共圆（限量版）板块一：辅助圆思想平面几何中有很多题中的背景并没出现圆，但是在解题过程中我们会发现，如果能够适当添加辅助圆，不仅能让题目瞬间变得简单，同时还可能会有意想不到的收获，得到很多有趣的结论，而且纵观这几年中考命题趋势，第24题的几何综合题越来越需要我们有辅助圆的思想和思维了，而辅助圆思想又是学习四点共圆的基础.构造辅助圆的基本思路：1、共顶点，等线段想辅助圆（圆的定义）；2、不共线的三点确定一个圆（即做这个三角形的外接圆）；3、利用四点共圆的判定作辅助圆.1、如图，在四边形ABCD中，AB=AC=AD,∠BCD=150°，求∠BAD的度数.DCBA2、（大兴期末）已知四边形ABCD，A B∥CD,且AB=AC=AD=a,BC=b,且2a＞b求cos DBA∠的值.3、（2014年海淀一模）在△ABC中，AB=AC，将线段AC绕着点C逆时针旋转得到线段CD，旋转角为α，且0180α<<，连接AD、BD．（1）如图1，当∠BAC=100°，60α=时，∠CBD 的大小为_________；（2）如图2，当∠BAC=100°，20α=时，求∠CBD的大小；（3）已知∠BAC的大小为m（60120m<<），若∠CBD的大小与（2）中的结果相同，请直接写出α的大小．图2DCBA图1AB C4、（2011海淀期末）如图，E ，B ，A ，F 四点共线，点D 是正三角形ABC 的边AC 的中点， 点P 是直线AB 上异于A ，B 的一个动点，且满足30CPD ∠=︒，则（ ）A ．点P 一定在射线BE 上B ．点P 一定在线段AB 上C ．点P 可以在射线AF 上 ，也可以在线段AB 上D ．点P 可以在射线BE 上 ，也可以在线段5、（2011西城一模）平面直角坐标系xOy 中，抛物线244y ax ax a c=-++与x轴交于点A 、点B ， 与y 轴的正半轴交于点C ，点 A 的坐标为(1, 0)，OB =OC ， 抛物线的顶点为D ． (1) 求此抛物线的解析式；(2) 若此抛物线的对称轴上的点P 满足∠APB =∠ACB ，求点P 的坐标；(3) Q 为线段BD 上一点，点A 关于∠AQB 的平分线的对称点为A '，若2=-QB QA 求点Q 的坐标和此时△QAA '的面积．C6、（2013海淀期中）初三（1）班的同学们在解题过程中，发现了几种利用尺规作一个角的半角的方法．题目：在△ABC中，80ACB∠=︒，求作：40ADB∠=︒．图1 图2仿照他们的做法，利用尺规作图解决下列问题，要求保留作图痕迹．（1）请在图1和图2中分别出作20APB∠=︒；（2）当60ACB∠=︒时，在图3中作出30APB∠=︒，且使点P在直线l上．lACBDACB EA B板块二：四点共圆判定：1、到一定点的距离相等的四个点共圆（圆的定义） 2、共斜边的直角三角形的顶点共圆 （圆的定义）（此判定考察最多）3、同底且同侧张角相等的两个三角形的顶点共圆 （同弧所对圆周角相等逆定理）4、对角互补或有一个外角等于其内对角的四边形的顶点共圆（圆内接四边形逆定理）另注：四点共圆的判定还有很多，我们只讲中考中涉及到的这四种，其实基本上所有的圆幂 定理的逆定理都可以判定四点共圆，比如相交弦定理，切割线定理及推论，托勒密定 理等.有兴趣的同学等暑假我们再讲.用途：圆中的性质很多，知道四点共圆后，我们可以利用其性质去解决一些几何证明题，判 断动点轨迹题及动点最值问题等，就会显得山穷水尽疑无路，柳暗花明又一村.7、证明判定3和4的成立（反证法）8、（海淀）已知：AOB △中，2AB OB ==，COD △中，3CD OC ==,ABO DCO =∠∠.连接AD 、BC ，点M 、N 、P 分别为OA 、OD 、BC 的中点.图1 (1) 如图1，若A 、O 、C 三点在同一直线上，且60ABO =∠，则PMN △的形状是________________，此时ADBC=________； (2) 如图2，若A 、O 、C 三点在同一直线上，且2ABO α=∠，证明PMN BAO △∽△，并计算ADBC的值(用含α的式子表示)； (3) 在图2中，固定AOB △，将COD △绕点O 旋转，直接写出PM 的最大值.9（海淀）如图一，在△ABC 中，分别以AB ，AC 为直径在△ABC 外作半圆1O 和半圆2O ，其中1O 和2O 分别为两个半圆的圆心. F 是边BC 的中点，点D 和点E 分别为两个半圆圆弧的中点.（1）连结1122,,,,,O F O D DF O F O E EF ，证明：12DO F FO E △≌△；（2）如图二，过点A 分别作半圆1O 和半圆2O 的切线，交BD 的延长线和CE 的延长线于点P 和点Q ，连结PQ ，若∠ACB =90°,DB =5，CE =3，求线段PQ 的长;（3）如图三，过点A 作半圆2O 的切线，交CE 的延长线于点Q ，过点Q 作直线F A 的垂线，交BD 的延长线于点P ，连结P A . 证明：P A 是半圆1O 的切线.图一A B CDE1O 2O 2O 1O AE B DP图二AB CEFDPQ1O 2O 图三10、（海淀期末） 如图，以(0,1)G 为圆心，半径为2的圆与x 轴交于A 、B 两点,与y 轴交于C 、D 两点,点E 为⊙G 上一动点，CF AE ⊥于F .当点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径长为（ ） A ． 32π B ．33π C ．34π D ．36π11、（2014年房山一模） 将等腰Rt △ABC 和等腰Rt △ADE 按图1方式放置，∠A=90°， AD 边与AB 边重合， AB ＝2AD ＝4．将△ADE 绕点A 逆时针方向旋转一个角度α（0°≤α≤180°），BD 的延长线交直线CE 于点P .（1）如图2，BD 与CE 的数量关系是 , 位置关系是 ； （2）在旋转的过程中，当AD ⊥BD 时，求出CP 的长； （3）在此旋转过程中，求点P 运动的路线长.12、（2012朝阳）在矩形ABCD 中，点P 在AD 上，AB =2，AP =1，将三角板的直角顶点放在点P 处，三角板的两直角边分别能与AB 、BC 边相交于点E 、F ，连接EF ． （1）如图，当点E 与点B 重合时，点F 恰好与点C 重合，求此时PC 的长；（2）将三角板从（1）中的位置开始，绕点P 顺时针旋转，当点E 与点A 重合时停止，在这个过程中，请你观察、探究并解答：① ∠PEF 的大小是否发生变化？请说明理由；② 直接写出从开始到停止，线段EF 的中点所经过的路线长．(0,1)I 图1图2DB EB ABA备用图D F A B E13、（2015北京四中12月月考）如图，在边长为2的菱形ABCD 中，∠A =60°，M是AD 边的中点，N 是AB 边上一动点，将△AMN 沿MN 所在的直线翻折得到△A'MN ，连接A'C ,则A'C 长度的最小值是_______.14、（2013昌平一模）在△ABC 中，AB =4，BC =6，∠ACB =30°，将△ABC 绕点B 按逆时针方向旋转，得到△A 1BC 1．（1）如图1，当点C 1在线段CA 的延长线上时，求∠CC 1A 1的度数； （2）如图2，连接AA 1，CC 1．若△CBC 1的面积为3，求△ABA 1的面积；（3）如图3，点E 为线段AB 中点，点P 是线段AC 上的动点，在△ABC 绕点B 按逆时针方向旋转的过程中，点P 的对应点是点P 1，直接写出线段EP 1长度的最大值与最小值．C 1C BA 1A图2A 1C 1ABC图1图3PP 1E A 1A C 115、（2013通州期末）在平面直角坐标系xOy 中，点B (0，3)，点C 是x 轴正半轴上一点，连结BC ，过点C 作直线CP ∥y 轴. （1）若含45°角的直角三角形如图所示放置．其中，一个顶点与点O 重合，直角顶点D在线段BC 上，另一个顶点E 在CP 上．求点C 的坐标； （2）若含30°角的直角三角形一个顶点与点O 重合，直角顶点D 在线段BC 上，另一个顶点E 在CP 上，求点C 的坐标．备用图备用图第24题图。

四点共圆知识点总结四点共圆是指如果四个点A、B、C、D在同一圆上，那么称这四个点共圆。

四点共圆是圆的性质之一，也是解几何问题中常见的题型。

在这篇文章中，我将对四点共圆的性质、证明方法、应用以及相关定理进行总结和归纳。

一、四点共圆的性质1. 四点共圆的定义四点共圆是指若四个点A、B、C、D在同一圆上，那么称这四个点共圆。

这就是四点共圆的基本定义。

2. 四点共圆的性质四点共圆具有以下性质：（1）任意三个点共圆，那么这三点构成的圆上的所有点也共圆。

（2）如果四个点共圆，那么这四个点所在的圆是唯一的。

3. 四点共圆的方法确定四点共圆的方法一般有以下几种：（1）利用圆的性质，通过证明四个点在同一圆上，从而得出四点共圆的结论。

（2）通过等角的关系来证明四点共圆。

二、证明四点共圆的方法1、利用圆的性质证明四点共圆的方法之一是利用圆的性质。

根据圆的性质，我们可以利用圆的直径、相交弦的性质等进行证明。

比如，通过证明四边形的对角线互相平分、垂直平分或者等长等等，从而得出四点共圆的结论。

2、利用等角关系利用等角的关系也是证明四点共圆的一种常见方法。

当我们能够找到四点共圆的特殊角度关系时，就可以得出四点共圆的结论。

比如，利用相交弦与此弦的交点处的两个相等角，利用垂径定理等等。

三、四点共圆在解题中的应用四点共圆是解几何问题中常见的题型，尤其是在证明题中经常会用到四点共圆的性质。

常见的应用有以下几个方面：1、辅助证明定理在证明定理的过程中，我们经常需要利用四点共圆的性质来推出结论。

比如，证明一个四边形为菱形或者矩形时，就可以利用四点共圆的性质。

2、判断点的位置在解题过程中，有时需要判断一个点是否在同一圆上，这就需要利用四点共圆的性质来确定。

3、证明等价关系在解题中，有时候需要利用四点共圆的性质来证明等价关系，比如利用四点共圆来证明辅助线与所给线段平行等等。

四、四点共圆的相关定理在几何中，和四点共圆相关的定理较多，下面介绍几个常见的定理：1、相交弦定理在一个圆上，如果两条弧所对的两条弦相交，那么这两个相交点和弦的两端点构成的四个点共圆。

四点共圆一、知识点梳理1、四点共圆的概念如果同一平面内的四个点在同一个圆上，则称这四个点共圆，一般简称为“四点共圆”。

性质：①圆内接四边形的对角互补；②圆内接四边形的一个外角等于它的内对角。

2、初中阶段四点共圆的常见判定方法（1）共底边的两个直角三角形，则四个顶点共圆，且直角三角形的斜边为圆的直径。

（2）共底边的两个三角形顶角相等，且在底边的同侧，则四个顶点共圆。

（3）对于凸四边形ABCD ，对角互补⇔四点共圆。

（4）相交弦定理的逆定理：对于凸四边形ABCD 其对角线AC 、BD 交于P ，PD BP PC AP ⋅=⋅⇔四点共圆。

（5）割线定理：对于凸四边形ABCD 其边的延长线AB 、CD 交于P ，PD PC PB PA ⋅=⋅⇔四点共圆。

ABCDPAB CDP3、四点共圆的妙用巧用四点共圆可以帮助我们在解题过程中快速地求角等、边等、相似、边长等问题。

二、例题精练1、四点共圆的性质a.例题讲解1．四边形ABCD内接于⊙O，则∠A：∠B：∠C：∠D的值可以是（）A．1：2：3：4 B．1：3：2：4 C．1：4：2：3 D．1：2：4：32．如图，AB经过圆心O，四边形ABCD内接于⊙O，∠B=3∠BAC，则∠ADC的度数为（）A．100°B．°C．120°D．135°3．如图，点A，B，C，D在⊙O上，=，∠CAD=30°，∠ACD=50°，则∠ADB=．4.如图，在圆内接四边形ABCD中，∠A=60°，∠B=90°，AB=2，CD=1，求BC 的长8．已知：如图，四边形ABCD是⊙O的内接四边形，直径DG交边AB于点E，AB、DC的延长线相交于点F．连接AC，若∠ACD=∠BAD．（1）求证：DG⊥AB；（2）若AB=6，tan∠FCB=3，求⊙O半径．DCBAb.举一反三1．如图，四边形ABCD内接于⊙O，∠DAB=140°，连接OC，点P是半径OC上一点，则∠BPD不可能为（）A．40°B．60°C．80°D．90°2．如图，四边形ABCD内接于⊙O，它的一个外角∠EBC=65°，分别连接AC，BD，若AC=AD，则∠DBC的度数为（）A．50°B．55°C．65°D．70°3．如图，A、B、C、D四个点在同一个圆上，∠ADC=90°，AB=7cm，CD=5cm，AE=4cm，CF=6cm，则阴影部分的面积为cm2．4．如图，⊙O为△ABC的外接圆，且AB=AC，过点A的直线交⊙O于D，交BC 延长线于F，DE是BD的延长线，连接CD．（1）求证：∠EDF=∠CDF；（2）求证：AB2=AF•AD；（3）若BD是⊙O的直径，且∠EDC=120°，BC=6cm，求AF的长．2、四点共圆的妙用之边角问题a.例题讲解1.如图，矩形ABCD 的对角线AC、BD 相交于点O，过点O 作OE⊥AC 交AB 于E,若BC=4，△AOE 的面积为6，则cos∠BOE= .2.如图，正方形ABCD的中心为O点，面积为25；点P为正方形内一点，且∠OPB=45°，PA：PB=3:4，则PB=3.在直线ABC的同一侧作两个等边三角形△ABD和△BCE，连接AE与CD，证明：（1）△ABE≌△DBC；（2）AE=DC；（3）AE与DC的夹角为60°；（4）△AGB≌△DFB；（5）△EGB≌△CFB；（6）BH平分∠AHC；GF∥ACHFGEDA C4.四边形ABCD是正方形，AC 与BD，相交于点O，点E、F 是直线AD上两动点，且AE =DF，CF所在直线与对角线BD所在直线交于点G ，连接AG ，直线AG 交BE 于点H ．（1）如图1，当点E 、F 在线段AD 上时，①求证：∠DAG=∠DCG；②猜想AG 与BE 的位置关系，并加以证明；（2）如图2，在（1）条件下，连接HO，试说明HO 平分∠BHG；b.举一反三1.在ABC ∆的边AB ，BC ，CA 上分别取D ，E ，F ．使得BE DE =，CE FE =，又点O 是ADF ∆的外心． 求证：O 在DEF ∠的平分线上．C2.如图，已知ABC ∆中的两条角平分线AD 和CE 相交于H ，︒=∠60B ，F 在AC 上，且AF AE =． 求证：CE 平分DEF ∠．B3.已知AD 是ABC ∆角平分线交BC 于D ，ABD ACD ABC ∆∆∆、、外心分别是12O O O 、、,求证12=O O OO2.如图，AB 为圆O 的直径，CD 为垂直于AB 的一条弦，垂足为E ，弦BM 与CD 交于点F ．（1）证明：A 、E 、F 、M 四点共圆；（2）证明：22AB BM BF AC =⋅+．ABb.举一反三1.如图，已知BA 是⊙O 的直径，AD 是⊙O 的切线，割线BD 、BF 分别交⊙O 于C 、E ，连接AE 、CE ．求证：BD BC BF BE ⋅=⋅．B AF三、演练场1．（2014•东营）如图，四边形ABCD 为菱形，AB=BD ，点B 、C 、D 、G 四个点在同一个圆⊙O 上，连接BG 并延长交AD 于点F ，连接DG 并延长交AB 于点E ，BD 与CG 交于点H ，连接FH ，下列结论：①AE=DF；②FH∥AB；③△DGH∽△BGE；④当CG 为⊙O 的直径时，DF=AF ． 其中正确结论的个数是（ ）A．1 B．2 C．3 D．42．（2017•扬州）如图，已知正方形ABCD的边长为4，点P是AB边上的一个动点，连接CP，过点P作PC的垂线交AD于点E，以 PE为边作正方形PEFG，顶点G在线段PC上，对角线EG、PF相交于点O．（1）若AP=1，则AE= ；（2）①求证：点O一定在△APE的外接圆上；②当点P从点A运动到点B时，点O也随之运动，求点O经过的路径长；（3）在点P从点A到点B的运动过程中，△APE的外接圆的圆心也随之运动，求该圆心到AB边的距离的最大值．3．（2018•路南区三模）如图1，已知∠MAN=60°，点B在射线AM上，AB=4，点P为直线AN上一动点，以BP为边作等边△BPQ（点B，P，Q按顺时针排列），点O是△BPQ的外心．（1）当OB⊥AM时，点O ∠MAN的平分线上（填“在”或“不在”）；（2）如图2，当点P在射线AN上运动（点P与点A不重合）时，求证：点O 在∠MAN的平分线上；（3）如图2，当点P在射线AN上运动（点P与点A不重合）时，AO与BP交于点C，求证：△ABO∽△ACP；设AP=m，直接写出AC•AO的值（用含m的式子表示）；（4）若点D在射线AN上，AD=2，⊙K为△ABD的内切圆，当△BPQ的边BP与⊙K相切时，请直接写出点A与点O的距离．4．（2018春•历下区期末）如图，已知菱形ABCD边长为4，BD=4，点E从点A出发沿着AD、DC方向运动，同时点F从点D出发以相同的速度沿着DC、CB的方向运动．（1）如图1，当点E在AD上时，连接BE、BF，试探究BE与BF的数量关系，并证明你的结论；（2）在（1）的前提下，求EF的最小值和此时△BEF的面积；（3）当点E运动到DC边上时，如图2，连接BE、DF，交点为点M，连接AM，则∠AMD大小是否变化请说明理由．5．（2018•泉州二模）如图1，在矩形ABCD中，AB=，AD=3，点E从点B出发，沿BC边运动到点C，连结DE，过点E作DE的垂线交AB于点F．（1）求证：∠BFE=∠ADE；（2）求BF的最大值；（3）如图2，在点E的运动过程中，以EF为边，在EF上方作等边△EFG，求边EG的中点H所经过的路径长．6．（2015秋•南岸区期末）在正方形ABCD中，点E是对角线AC的中点，点F 在边CD上，连接DE、AF，点G在线段AF上（1）如图①，若DG是△ADFD的中线，DG=，DF=3，连接EG，求EG的长；（2）如图②，若DG⊥AF交AC于点H，点F是CD的中点，连接FH，求证：∠CFH=∠AFD；（3）如图③，若DG⊥AF交AC于点H，点F是CD上的动点，连接EG．当点F 在边CD上（不含端点）运动时，∠EGH的大小是否发生改变若不改变，求出∠EGH的度数；若发生改变，请说明理由．。

四点共圆判定定理推导过程四点共圆判定定理，听起来好像很复杂，其实一点也不难，咱们一起来聊聊。

想象一下，你和几个朋友在公园里，玩着有趣的接力赛。

突然，有人提议要画一个圆，看看这几个点能不能在这个圆上面。

于是，你们就开始思考，这四个点究竟能不能“共圆”呢？咱们要知道什么是“共圆”。

简单来说，就是说这几个点都在同一个圆上，大家一起享受这个圆的乐趣。

如果你有过画圆的经验，就会发现，要想让几个点都在一个圆上可不是那么简单的事。

就像你找不到一个合适的地方放所有的零食一样，得想办法！不过，别担心，四点共圆的判断其实有个很简单的方法。

我们可以用一个很实用的公式来解决这个问题。

你只需要先找到这四个点的坐标，记得要准确哦，不然就像在拍照时没对焦，出来的效果可就大打折扣。

咱们可以组成一个行列式，听起来有点高大上，其实就是把这几个点的坐标填到一个特定的表格里。

这个表格里有点像做饭时的食材清单，缺少一个材料可就不能成菜。

然后，把这些坐标填进一个特定的行列式，算一算，最后结果出来了。

如果这个行列式的值等于零，那就恭喜你，四个点真的能共圆；如果不等于零，哎，那就得另想办法了。

这就像做数学题，答案对了就是对的，不对就得改正。

相信我，掌握这个方法，你再也不用担心和朋友们的接力赛了，圆圆满满，大家都开心。

再说说这行列式。

大家可能觉得行列式听起来很抽象，实际上这东西就像是做某种约定。

只要这四个点能满足某种关系，它们就可以欢快地站在同一个圆上。

别看这小小的行列式，它其实在数学里可是个大明星，很多地方都能见到它的身影，就像你在街上总能遇到的熟人，随时准备给你带来意想不到的惊喜。

顺便提一句，四点共圆的定理在我们的生活中也有很多应用。

比如说，很多设计师在设计花坛、操场的时候，都会考虑这些点的关系。

想象一下，一个完美的花坛，每一朵花、每一片草都恰好围绕着中心展开，真的是美得不可思议。

就像生活中的各种聚会，大家围坐在一起，气氛和谐，快乐分享，简直太棒了。

初中四点共圆的判定定理初中数学里有个很有趣的定理，叫做“四点共圆的判定定理”。

听起来是不是有点高大上？其实说白了就是：四个点如果能在同一个圆上，那它们之间的关系可是很特别的哦。

想象一下，四个好朋友，围成一圈，聊聊天，玩玩耍，生活多美好。

要是这四个点真能共圆，那可就意味着它们之间的角度关系得特别好，这个可不是随便说说的。

我们得聊聊什么是共圆。

简单来说，四个点能在一个圆上，就是说这四个点到圆心的距离是一样的。

这就像我们在生活中，有些朋友总是能聚在一起，无论走到哪里，关系都特别紧密。

好比说，吃饭时大家一起点的菜，总是能让每个人满意，恰到好处，圆满得很。

这就是共圆的魅力呀！怎么判断这四个点能不能共圆呢？其实很简单，大家只需要掌握一个小窍门。

记住了，四个点要共圆，就得看它们的对角线交点，看看这条线的乘积是否相等。

听上去可能有点复杂，但实际上就像打麻将一样，运气来了，胡牌就是这么简单。

只要细心算一下，就能得出结论，谁和谁能一圈儿走到一起。

这不，就拿生活中的事来举个例子。

假如有四个小伙伴，分别是小明、小红、小刚和小丽。

他们一起去游乐场玩，特别开心。

小明跟小红的关系特别好，像那对小鸳鸯，真是让人羡慕。

但小刚和小丽却有点小隔阂，感觉总是打不到一块儿。

这时候，若是他们能找到一个共同的兴趣，或者一起完成个任务，哎呀，那关系可就像那四个共圆的点一样，慢慢就能拉近了。

再说了，四点共圆的定理在生活中还可以提醒我们，朋友之间的关系也是要保持平衡的。

就像一个圆，缺了哪一块儿都不行。

要是某个朋友总是偏心，那就容易让其他人感到不舒服。

想想，我们的生活不就是要和谐、圆满吗？和朋友之间的相处也是如此。

当然了，这个定理还有个特别的地方，涉及到圆的外接圆。

四个点要是共圆，那就得存在一个圆把它们都包住。

这个圆就像我们生活中的大怀抱，能容纳各种不同的朋友，让大家在一起，互相包容，互相理解。

这就像家人一样，无论发生什么，始终围绕在一起，心连心。