Photon Interactions in Matter and Effect on Organ Systemsppt在物质与效应器官systemsppt光子相互作用
- 格式:ppt
- 大小:802.07 KB
- 文档页数:43


工程光学培养方案英文1. IntroductionEngineering optics is an important branch of applied optics that focuses on the application of optical principles and theories to the design and development of optical systems for various applications. A comprehensive training plan in engineering optics is essential for students or professionals who are interested in pursuing a career in this field. This training plan provides a detailed outline of the key topics and skills that should be covered in an engineering optics training program.2. Basic Optical PrinciplesThe training program should begin with a solid foundation in the basic principles of optics, including geometric optics, wave optics, and quantum optics. Key topics to cover in this section include reflection and refraction, lens and mirror equations, interference and diffraction phenomena, and photon interactions with matter. The goal is to provide students with a fundamental understanding of how light behaves and interacts with different optical elements.3. Optical Materials and CoatingsNext, the training plan should include a section on optical materials and coatings. This should cover the various types of materials used in optical systems, including glasses, crystals, and polymers, as well as the different types of optical coatings used to enhance the performance of optical components. Students should also learn about the properties of these materials and how they affect the performance of optical systems.4. Optical InstrumentationThe training program should include a comprehensive section on optical instrumentation, covering a wide range of optical devices and systems. This may include topics such as imaging systems, spectroscopy instruments, laser systems, and optical sensors. Students should learn about the design, operation, and performance of these systems, as well as the specific applications for which they are used.5. Optical Design and AnalysisAnother critical aspect of engineering optics training is the design and analysis of optical systems. This should include topics such as optical design software, lens and mirror design, optical aberrations, and optimization techniques. Students should also learn about the process of simulating and testing optical systems using computer-aided design tools.6. Optical Manufacturing and TestingIn addition to design and analysis, the training plan should cover the manufacturing and testing of optical systems. This should include topics such as precision machining, polishingand coating processes, and metrology techniques for evaluating the performance of optical components. Students should gain practical experience in manufacturing and testing optical systems through hands-on laboratory exercises.7. Optical Systems Integration and IntegrationFurthermore, a good training plan in engineering optics should cover the integration and alignment of optical systems. This should include topics such as optical system integration, optical alignment, and the use of mechanical and opto-mechanical components. Students should also learn about the processes involved in calibrating and aligning optical systems for optimal performance.8. Applications of Engineering OpticsFinally, the training program should include a section on the diverse applications of engineering optics. This may include topics such as telecommunications, medical imaging, industrial metrology, remote sensing, and defense systems. Students should learn how engineering optics is applied in real-world scenarios and gain an understanding of the various industries and fields where optical systems are critical.9. Laboratory and Project WorkThroughout the training program, students should have opportunities to apply their theoretical knowledge in practical and hands-on laboratory exercises. They should also be encouraged to participate in projects that involve the design, construction, and testing of optical systems for specific applications. This hands-on experience is essential for reinforcing theoretical concepts and developing practical skills.10. ConclusionIn conclusion, a comprehensive training plan in engineering optics should cover a wide range of topics, including basic optical principles, optical materials and coatings, optical instrumentation, optical design and analysis, optical manufacturing and testing, optical systems integration and alignment, applications of engineering optics, as well as laboratory and project work. By following such a training plan, students and professionals can gain a solid foundation in engineering optics and develop the skills necessary for a successful career in this field.。

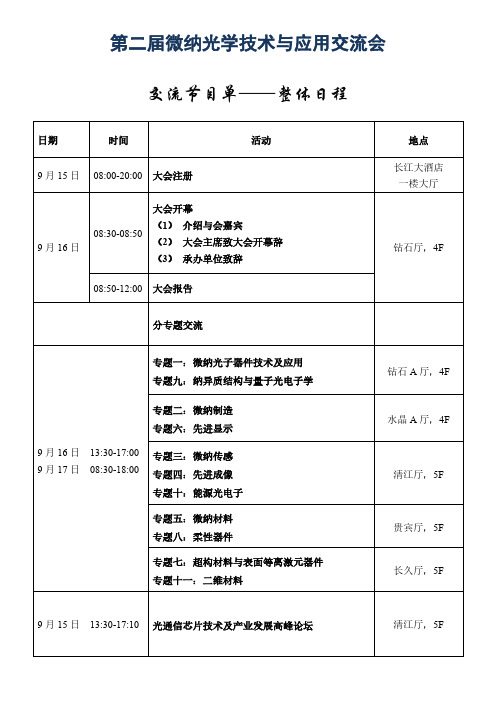
第二届微纳光学技术与应用交流会交流节目单——整体日程
交流节目单——大会报告地点:钻石厅,4F
交流节目单——分专题报告
专题一:微纳光子器件技术及应用
专题九:纳异质结构与量子光电子学
地点:钻石A厅,4F
专题二:微纳制造
专题六:先进显示地点:水晶A厅,4F
专题三:微纳传感
专题四:先进成像
专题十:能源光电子地点:清江厅,5F
专题五:微纳材料
专题八:柔性器件地点:贵宾厅,5F
专题七:超构材料与表面等离激元器件
专题十一:二维材料
地点:长久厅,5F
光通信芯片技术及产业发展高峰论坛。

More informationPhase Noise and Frequency Stability in OscillatorsPresenting a comprehensive account of oscillator phase noise and frequency stability,this practical text is both mathematically rigorous and accessible.An in-depth treatmentof the noise mechanism is given,describing the oscillator as a physical system,andshowing that simple general laws govern the stability of a large variety of oscillatorsdiffering in technology and frequency range.Inevitably,special attention is given to am-plifiers,resonators,delay lines,feedback,andflicker(1/f)noise.The reverse engineeringof oscillators based on phase-noise spectra is also covered,and end-of-chapter exercisesare given.Uniquely,numerous practical examples are presented,including case studiestaken from laboratory prototypes and commercial oscillators,which allow the oscillatorinternal design to be understood by analyzing its phase-noise spectrum.Based on tuto-rials given by the author at the Jet Propulsion Laboratory,international IEEE meetings,and in industry,this is a useful reference for academic researchers,industry practitioners,and graduate students in RF engineering and communications engineering.Additional materials are available via /rubiola.Enrico Rubiola is a Senior Scientist at the CNRS FEMTO-ST Institute and a Professorat the Universit´e de Franche Comt´e.With previous positions as a Professor at theUniversit´e Henri Poincar´e,Nancy,and in Italy at the University Parma and thePolitecnico di Torino,he has also consulted at the NASA/Caltech Jet PropulsionLaboratory.His research interests include low-noise oscillators,phase/frequency-noisemetrology,frequency synthesis,atomic frequency standards,radio-navigation systems,precision electronics from dc to microwaves,optics and gravitation.More informationThe Cambridge RF and Microwave Engineering SeriesSeries EditorSteve C.CrippsPeter Aaen,Jaime Pl´a and John Wood,Modeling and Characterization of RF andMicrowave Power FETsEnrico Rubiola,Phase Noise and Frequency Stability in OscillatorsDominique Schreurs,M´a irt´ın O’Droma,Anthony A.Goacher and Michael Gadringer,RF Amplifier Behavioral ModelingFan Y ang and Y ahya Rahmat-Samii,Electromagnetic Band Gap Structures in AntennaEngineeringForthcoming:Sorin V oinigescu and Timothy Dickson,High-Frequency Integrated CircuitsDebabani Choudhury,Millimeter W aves for Commercial ApplicationsJ.Stephenson Kenney,RF Power Amplifier Design and LinearizationDavid B.Leeson,Microwave Systems and EngineeringStepan Lucyszyn,Advanced RF MEMSEarl McCune,Practical Digital Wireless Communications SignalsAllen Podell and Sudipto Chakraborty,Practical Radio Design TechniquesPatrick Roblin,Nonlinear RF Circuits and the Large-Signal Network AnalyzerDominique Schreurs,Microwave Techniques for MicroelectronicsJohn L.B.Walker,Handbook of RF and Microwave Solid-State Power AmplifiersPhase Noise and Frequency Stability in OscillatorsENRICO RUBIOLAProfessor of Electronics FEMTO-ST Institute CNRS and Universit´e de Franche Comt´e Besanc ¸on,FranceMore informationMore informationCAMBRIDGE UNIVERSITY PRESSCambridge,New Y ork,Melbourne,Madrid,Cape Town,Singapore,S˜a o Paulo,DelhiCambridge University PressThe Edinburgh Building,Cambridge CB28RU,UKPublished in the United States of America by Cambridge University Press,New Y orkInformation on this title:/9780521886772C Cambridge University Press2009This publication is in copyright.Subject to statutory exceptionand to the provisions of relevant collective licensing agreements,no reproduction of any part may take place withoutthe written permission of Cambridge University Press.First published2009Printed in the United Kingdom at the University Press,CambridgeA catalog record for this publication is available from the British LibraryISBN978-0-521-88677-2hardbackCambridge University Press has no responsibility for the persistence oraccuracy of URLs for external or third-party internet websites referred toin this publication,and does not guarantee that any content on suchwebsites is,or will remain,accurate or appropriate.More informationContentsForeword by Lute Maleki page ixForeword by David Leeson xiiPreface xv How to use this book xviSupplementary material xviii Notation xix 1Phase noise and frequency stability11.1Narrow-band signals11.2Physical quantities of interest51.3Elements of statistics91.4The measurement of power spectra131.5Linear and time-invariant(LTI)systems191.6Close-in noise spectrum221.7Time-domain variances251.8Relationship between spectra and variances291.9Experimental techniques30Exercises33 2Phase noise in semiconductors and amplifiers352.1Fundamental noise phenomena352.2Noise temperature and noisefigure372.3Phase noise and amplitude noise422.4Phase noise in cascaded amplifiers492.5 Low-flicker amplifiers522.6 Detection of microwave-modulated light62Exercises65 3Heuristic approach to the Leeson effect673.1Oscillator fundamentals673.2The Leeson formula72More informationvi Contents3.3The phase-noise spectrum of real oscillators753.4Other types of oscillator824Phase noise and feedback theory884.1Resonator differential equation884.2Resonator Laplace transform924.3The oscillator964.4Resonator in phase space1014.5Proof of the Leeson formula1114.6Frequency-fluctuation spectrum and Allan variance1164.7 A different,more general,derivation of the resonatorphase response1174.8 Frequency transformations1215Noise in delay-line oscillators and lasers1255.1Basic delay-line oscillator1255.2Optical resonators1285.3Mode selection1305.4The use of a resonator as a selectionfilter1335.5Phase-noise response1385.6Phase noise in lasers1435.7Close-in noise spectra and Allan variance1455.8Examples1466Oscillator hacking1506.1General guidelines1506.2About the examples of phase-noise spectra1546.3Understanding the quartz oscillator1546.4Quartz oscillators156Oscilloquartz OCXO8600(5MHz AT-cut BV A)156Oscilloquartz OCXO8607(5MHz SC-cut BV A)159RAKON PHARAO5MHz quartz oscillator162FEMTO-ST LD-cut quartz oscillator(10MHz)164Agilent10811quartz(10MHz)166Agilent noise-degeneration oscillator(10MHz)167Wenzel501-04623(100MHz SC-cut quartz)1716.5The origin of instability in quartz oscillators1726.6Microwave oscillators175Miteq DRO mod.D-210B175Poseidon DRO-10.4-FR(10.4GHz)177Poseidon Shoebox(10GHz sapphire resonator)179UWA liquid-N whispering-gallery9GHz oscillator182More informationContents vii6.7Optoelectronic oscillators185NIST10GHz opto-electronic oscillator(OEO)185OEwaves Tidalwave(10GHz OEO)188 Exercises190Appendix A Laplace transforms192References196Index202More informationForeword by Lute MalekiGiven the ubiquity of periodic phenomena in nature,it is not surprising that oscillatorsplay such a fundamental role in sciences and technology.In physics,oscillators are thebasis for the understanding of a wide range of concepts spanningfield theory and linearand nonlinear dynamics.In technology,oscillators are the source of operation in everycommunications system,in sensors and in radar,to name a few.As man’s study ofnature’s laws and human-made phenomena expands,oscillators have found applicationsin new realms.Oscillators and their interaction with each other,usually as phase locking,and withthe environment,as manifested by a change in their operational parameters,form thebasis of our understanding of a myriad phenomena in biology,chemistry,and evensociology and climatology.It is very difficult to account for every application in whichthe oscillator plays a role,either as an element that supports understanding or insight oran entity that allows a given application.In all thesefields,what is important is to understand how the physical parametersof the oscillator,i.e.its phase,frequency,and amplitude,are affected,either by theproperties of its internal components or by interaction with the environment in whichthe oscillator resides.The study of oscillator noise is fundamental to understanding allphenomena in which the oscillator model is used in optimization of the performance ofsystems requiring an oscillator.Simply stated,noise is the unwanted part of the oscillator signal and is unavoidablein practical systems.Beyond the influence of the environment,and the non-ideality ofthe physical elements that comprise the oscillator,the fundamental quantum nature ofelectrons and photons sets the limit to what may be achieved in the spectral purity of thegenerated signal.This sets the fundamental limit to the best performance that a practicaloscillator can produce,and it is remarkable that advanced oscillators can reach it.The practitioners who strive to advance thefield of oscillators in time-and-frequencyapplications cannot be content with knowledge of physics alone or engineering alone.The reason is that oscillators and clocks,whether of the common variety or the advancedtype,are complex“systems”that interact with their environment,sometimes in waysthat are not readily obvious or that are highly nonlinear.Thus the physicist is needed toidentify the underlying phenomenon and the parameters affecting performance,and theengineer is needed to devise the most effective and practical approach to deal with them.The present monograph by Professor Enrico Rubiola is unique in the extent to which itsatisfies both the physicist and the engineer.It also serves the need to understand bothMore informationx Forewordsthe fundamentals and the practice of phase-noise metrology,a required tool in dealingwith noise in oscillators.Rubiola’s approach to the treatment of noise in this book is based on the input–output transfer functions.While other approaches lead to some of the same results,this treatment allows the introduction of a mathematical rigor that is easily tractable byanyone with an introductory knowledge of Fourier and Laplace transforms.In particular,Rubiola uses this approach to obtain a derivation,fromfirst principles,of the Leesonformula.This formula has been used in the engineering literature for the noise analysisof the RF oscillator since its introduction by Leeson in1966.Leeson evidently arrivedat it without realizing that it was known earlier in the physics literature in a differentform as the Schawlow–Townes linewidth for the laser oscillator.While a number ofother approaches based on linear and nonlinear models exist for analyzing noise inan oscillator,the Leeson formula remains particularly useful for modeling the noisein high-performance oscillators.Given its relation to the Schawlow–Townes formula,it is not surprising that the Leeson model is so useful for analyzing the noise in theoptoelectronic oscillator,a newcomer to the realm of high-performance microwave andmillimeter-wave oscillators,which are also treated in this book.Starting in the Spring of2004,Professor Rubiola began a series of limited-timetenures in the Quantum Sciences and Technologies group at the Jet Propulsion Labo-ratory.Evidently,this can be regarded as the time when the initial seed for this bookwas conceived.During these visits,Rubiola was to help architect a system for themeasurement of the noise of a high-performance microwave oscillator,with the sameexperimental care that he had previously applied and published for the RF oscillators.Characteristically,Rubiola had to know all the details about the oscillator,its principleof operation,and the sources of noise in its every component.It was only then that hecould implement the improvement needed on the existing measurement system,whichwas based on the use of a longfiber delay in a homodyne setup.Since Rubiola is an avid admirer of the Leeson model,he was interested in applyingit to the optoelectronic oscillator,as well.In doing so,he developed both an approachfor analyzing the performance of a delay-line oscillator and a scheme based on Laplacetransforms to derive the Leeson formula,advancing the original,heuristic,approach.These two treatments,together with the range of other topics covered,should makethis unique book extremely useful and attractive to both the novice and experiencedpractitioners of thefield.It is delightful to see that in writing the monograph,Enrico Rubiola has so openlybared his professional persona.He pursues the subject with a blatant passion,andhe is characteristically not satisfied with“dumbing down,”a concept at odds withmathematical rigor.Instead,he provides visuals,charts,and tables to make his treatmentaccessible.He also shows his commensurate tendencies as an engineer by providingnumerical examples and details of the principles behind instruments used for noisemetrology.He balances this with the physicist in him that looks behind the obvious forthe fundamental causation.All this is enhanced with his mathematical skill,of which healways insists,with characteristic modesty,he wished to have more.Other ingredients,missing in the book,that define Enrico Rubiola are his knowledge of ancient languagesMore informationForewords xi and history.But these could not inform further such a comprehensive and extremelyuseful book on the subject of oscillator noise.Lute MalekiNASA/Caltech Jet Propulsion Laboratoryand OEwaves,Inc.,February2008More informationForeword by David LeesonPermit me to place Enrico Rubiola’s excellent book Phase Noise and Frequency Stabilityin Oscillators in context with the history of the subject over the pastfive decades,goingback to the beginnings of my own professional interest in oscillator frequency stability.Oscillator instabilities are a fundamental concern for systems tasked with keeping anddistributing precision time or frequency.Also,oscillator phase noise limits the demod-ulated signal-to-noise ratio in communication systems that rely on phase modulation,such as microwave relay systems,including satellite and deep-space parablyimportant are the dynamic range limits in multisignal systems resulting from the mask-ing of small signals of interest by oscillator phase noise on adjacent large signals.Forexample,Doppler radar targets are masked by ground clutter noise.These infrastructure systems have been well served by what might now be termedthe classical theory and measurement of oscillator noise,of which this volume is acomprehensive and up-to-date tutorial.Rubiola also exposes a number of significantconcepts that have escaped prior widespread notice.My early interest in oscillator noise came as solid-state signal sources began to beapplied to the radars that had been under development since the days of the MIT RadiationLaboratory.I was initiated into the phase-noise requirements of airborne Doppler radarand the underlying arts of crystal oscillators,power amplifiers,and nonlinear-reactancefrequency multipliers.In1964an IEEE committee was formed to prepare a standard on frequency stability.Thanks to a supportive mentor,W.K.Saunders,I became a member of that group,whichincluded leaders such as J.A.Barnes and L.S.Cutler.It was noted that the independentuse of frequency-domain and time-domain definitions stood in the way of the develop-ment of a common standard.To promote focused interchange the group sponsored theNovember1964NASA/IEEE Conference on Short Term Frequency Stability and editedthe February1966Special Issue on Frequency Stability of the Proceedings of the IEEE.The context of that time included the appreciation that self-limiting oscillators andmany systems(FM receivers with limiters,for example)are nonlinear in that theylimit amplitude variations(AM noise);hence the focus on phase noise.The modestfrequency limits of semiconductor devices of that period dictated the common usage ofnonlinear-reactance frequency multipliers,which multiply phase noise to the point whereit dominates the output noise spectrum.These typical circuit conditions were secondnature then to the“short-term stability community”but might not come so readily tomind today.More informationForewords xiii Thefirst step of the program to craft a standard that would define frequency stabilitywas to understand and meld the frequency-and time-domain descriptions of phaseinstability to a degree that was predictive and permitted analysis and optimization.Bythe time the subcommittee edited the Proc.IEEE special issue,the wide exchange ofviewpoints and concepts made it possible to synthesize concise summaries of the workin both domains,of which my own model was one.The committee published its“Characterization of frequency stability”in IEEE Trans.Instrum.Meas.,May1971.This led to the IEEE1139Standards that have served thecommunity well,with advances and revisions continuing since their initial publication.Rubiola’s book,based on his extensive seminar notes,is a capstone tutorial on thetheoretical basis and experimental measurements of oscillators for which phase noiseand frequency stability are primary issues.In hisfirst chapter Rubiola introduces the reader to the fundamental statistical de-scriptions of oscillator instabilities and discusses their role in the standards.Then in thesecond chapter he provides an exposition of the sources of noise in devices and circuits.In an instructive analysis of cascaded stages,he shows that,for modulative or parametricflicker noise,the effect of cascaded stages is cumulative without regard to stage gain.This is in contrast with the well-known treatment of additive noise using the Friisformula to calculate an equivalent input noise power representing noise that may originateanywhere in a cascade of real amplifiers.This example highlights the concept that“themodel is not the actual thing.”He also describes concepts for the reduction offlickernoise in amplifier stages.In his third chapter Rubiola then combines the elements of thefirst two chapters toderive models and techniques useful in characterizing phase noise arising in resonatorfeedback oscillators,adding mathematical formalism to these in the fourth chapter.Inthefifth chapter he extends the reader’s view to the case of delay-line oscillators suchas lasers.In his sixth chapter,Rubiola offers guidance for the instructive“hacking”ofexisting oscillators,using their external phase spectra and other measurables to estimatetheir internal configuration.He details cases in which resonatorfluctuations mask circuitnoise,showing that separately quantifying resonator noise can be fruitful and that devicenoisefigure and resonator Q are not merely arbitraryfitting factors.It’s interesting to consider what lies ahead in thisfield.The successes of today’sconsumer wireless products,cellular telephony,WiFi,satellite TV,and GPS,arise directlyfrom the economies of scale of highly integrated circuits.But at the same time thisintroduces compromises for active-device noise and resonator quality.A measure ofthe market penetration of multi-signal consumer systems such as cellular telephonyand WiFi is that they attract enough users to become interference-limited,often fromsubscribers much nearer than a distant base station.Hence low phase noise remainsessential to preclude an unacceptable decrease of dynamic range,but it must now beachieved within narrower bounds on the available circuit elements.A search for new understanding and techniques has been spurred by this requirementfor low phase noise in oscillators and synthesizers whose primary character is integrationand its accompanying minimal cost.This body of knowledge is advancing througha speculative and developmental phase.Today,numerical nonlinear circuit analysisMore informationxiv Forewordssupports additional design variables,such as the timing of the current pulse in nonlinearoscillators,that have become feasible because of the improved capabilities of bothsemiconductor devices and computers.Thefield is alive and well,with emerging players eager tofind a role on the stage fortheir own scenarios.Professionals and students,whether senior or new to thefield so ablydescribed by Rubiola,will benefit from his theoretical rigor,experimental viewpoint,and presentation.David B.LeesonStanford UniversityFebruary2008More informationPrefaceThe importance of oscillators in science and technology can be outlined by two mile-stones.The pendulum,discovered by Galileo Galilei in the sixteenth century,persistedas“the”time-measurement instrument(in conjunction with the Earth’s rotation period)until the piezoelectric quartz resonator.Then,it was not by chance that thefirst inte-grated circuit,built in September1958by Jack Kilby at the Bell Laboratories,was aradio-frequency oscillator.Time,and equivalently frequency,is the most precisely measured physical quantity.The wrist watch,for example,is probably the only cheap artifact whose accuracy ex-ceeds10−5,while in primary laboratories frequency attains the incredible accuracy ofa few parts in10−15.It is therefore inevitable that virtually all domains of engineeringand physics rely on time-and-frequency metrology and thus need reference oscillators.Oscillators are of major importance in a number of applications such as wireless com-munications,high-speed digital electronics,radars,and space research.An oscillator’srandomfluctuations,referred to as noise,can be decomposed into amplitude noise andphase noise.The latter,far more important,is related to the precision and accuracy oftime-and-frequency measurements,and is of course a limiting factor in applications.The main fact underlying this book is that an oscillator turns the phase noise of itsinternal parts into frequency noise.This is a necessary consequence of the Barkhausencondition for stationary oscillation,which states that the loop gain of a feedback oscillatormust be unity,with zero phase.It follows that the phase noise,which is the integral ofthe frequency noise,diverges in the long run.This phenomenon is often referred to asthe“Leeson model”after a short article published in1966by David B.Leeson[63].Onmy part,I prefer the term Leeson effect in order to emphasize that the phenomenon isfar more general than a simple model.In2001,in Seattle,Leeson received the W.G.Cady award of the IEEE International Frequency Control Symposium“for clear physicalinsight and[a]model of the effects of noise on oscillators.”In spring2004I had the opportunity to give some informal seminars on noise in oscil-lators at the NASA/Caltech Jet Propulsion Laboratory.Since then I have given lecturesand seminars on noise in industrial contexts,at IEEE symposia,and in universities andgovernment laboratories.The purpose of most of these seminars was to provide a tuto-rial,as opposed to a report on advanced science,addressed to a large-variance audiencethat included technicians,engineers,Ph.D.students,and senior scientists.Of course,capturing the attention of such a varied audience was a challenging task.The stimu-lating discussions that followed the seminars convinced me I should write a workingMore informationxvi Prefacedocument1as a preliminary step and then this book.In writing,I have made a seriouseffort to address the same broad audience.This work could not have been written without the help of many people.The gratitudeI owe to my colleagues and friends who contributed to the rise of the ideas containedin this book is disproportionate to its small size:R´e mi Brendel,Giorgio Brida,G.JohnDick,Michele Elia,Patrice F´e ron,Serge Galliou,Vincent Giordano,Charles A.(Chuck)Greenhall,Jacques Groslambert,John L.Hall,Vladimir S.(Vlad)Ilchenko,LaurentLarger,Lutfallah(Lute)Maleki,Andrey B.Matsko,Mark Oxborrow,Stefania R¨o misch,Anatoliy B.Savchenkov,Franc¸ois Vernotte,Nan Yu.Among them,I owe special thanks to the following:Lute Maleki for giving me theopportunity of spending four long periods at the NASA/Caltech Jet Propulsion Labora-tory,where I worked on noise in photonic oscillators,and for numerous discussions andsuggestions;G.John Dick,for giving invaluable ideas and suggestions during numerousand stimulating discussions;R´e mi Brendel,Mark Oxborrow,and Stefania R¨o misch fortheir personal efforts in reviewing large parts of the manuscript in meticulous detail andfor a wealth of suggestions and criticism;Vincent Giordano for supporting my effortsfor more than10years and for frequent and stimulating discussions.I wish to thank some manufacturers and their local representatives for kindness andprompt help:Jean-Pierre Aubry from Oscilloquartz;Vincent Candelier from RAKON(formerly CMAC);Art Faverio and Charif Nasrallah from Miteq;Jesse H.Searles fromPoseidon Scientific Instruments;and Mark Henderson from Oewaves.Thanks to my friend Roberto Bergonzo,for the superb picture on the front cover,entitled“The amethyst stairway.”For more information about this artist,visit the website.Finally,I wish to thank Julie Lancashire and Sabine Koch,of the Cambridge editorialstaff,for their kindness and patience during the long process of writing this book.How to use this bookLet usfirst abstract this book in one paragraph.Chapter1introduces the language ofphase noise and frequency stability.Chapter2analyzes phase noise in amplifiers,includ-ingflicker and other non-white phenomena.Chapter3explains heuristically the physicalmechanism of an oscillator and of its noise.Chapter4focuses on the mathematics thatdescribe an oscillator and its phase noise.For phase noise,the oscillator turns out to bea linear system.These concepts are extended in Chapter5to the delay-line oscillatorand to the laser,which is a special case of the latter.Finally,Chapter6analyzes indepth a number of oscillators,both laboratory prototypes and commercial products.Theanalysis of an oscillator’s phase noise discloses relevant details about the oscillator.There are other books about oscillators,though not numerous.They can be divided intothree categories:books on radio-frequency and microwave oscillators,which generallyfocus on the electronics;books about lasers,which privilege atomic physics and classical1E.Rubiola,The Leeson Effect–Phase Noise in Quasilinear Oscillators,February2005,arXiv:physics/0502143,now superseded by the present text.PrefacexviideeperreadingbasictheoreticaladvancedtheoreticallegendexperimentalistlecturerdeeperreadingFigure1Asymptotic reading paths:on the left,for someone planning lectures on oscillatornoise;on the right,for someone currently involved in practical work on oscillators.optics;books focusing on the relevant mathematical physics.The present text is uniquein that we look at the oscillator as a system consisting of more or less complex interactingblocks.Most topics are innovative,and the overlap with other books about oscillatorsor time-and-frequency metrology is surprisingly small.This may require an additionaleffort on the part of readers already familiar with the subject area.The core of this book rises from my experimentalist soul,which later became con-vinced of the importance of the mathematics.The material was originally thought anddrafted in the following(dis)order(see Fig.1):3Heuristic approach,6Oscillator hack-ing,4Feedback theory,5Delay-line oscillators.Thefinal order of subjects aims at amore understandable presentation.In seminars,I have often presented the material in the3–6–4–5order.Y et,the best reading path depends on the reader.T wo paths are suggestedin Fig.1for two“asymptotic”reader types,i.e.a lecturer and experimentalist.Whenplanning to use this book as a supplementary text for a university course,the lecturer More information。

脑灰质异位(FGMH )是一种较为少见的先天畸形,是神经元移行障碍性疾病的一种,在胚胎时期神经母细胞增殖迁移过程中受干扰因素的影响而发生[1]。
随着产前诊断技术的不断向深、细、精方向发展,本病越来越受到关注。
产前检查是一个特殊时期的检查,胎儿解剖结构上的影像学诊断主要依靠产前超声和MRI ,本病亦如此。
Blondiaux 等[2]研究了11例产前诊断的灰质异位胎儿,指出即使是针对性的产前超声对本病的诊断也是较难的;Manganaro 等[3]则指出胎儿MRI 早在孕19周胎儿就可对中枢神经系统结构进行良好的评价,但并未对产前超声与MRI 对本病的诊断进行对比研究;Teixeira 等[4]研究了后颅窝池囊肿和本病的相关性,11例中均存在有后颅窝池囊肿,提出当发现后颅窝池囊肿时应着重检查侧脑室的形态结构以排除室管膜下灰质异位。
总之以往研究报道侧重点各不相同,为探讨FGMH 的产前超声图像特征并评价其最佳产前诊断方法,本文在前人研究的基础上,通过对1例因脑室扩张来我院会诊的胎儿行颅脑针对性超声检查,发现侧脑室壁毛糙不规整等改变,并对近20年来的产前诊断本病的文献进行了回顾性分析,对比研究产前超声和MRI 对本病的检出率,以进一步丰富我们对胎儿大脑灰质异位的产前诊断、特征性的超声表现、合并畸形、临床表现以及预后等的认识。
1资料与方法1.1一般资料孕妇34岁,电子售后商,孕3产2,第1胎自然流产,胎儿胎儿脑灰质异位的产前诊断及文献回顾脑灰质异位的产前诊断及文献回顾张葵,李胜利,文华轩,袁鹰南方医科大学附属深圳市妇幼保健院超声科,广东深圳518028Prenatal diagnosis of fetal gray matter heteropia in one case and literature reviewZHAGN Kui,LI Shengli,WEN Huaxuan,YUAN YingDepartment of Ultrasound,Shenzhen Maternity &Child Healthcare Hospital Affiliated to Southern Medical University,Shen-zhen 518028,China摘要:目的探讨胎儿大脑灰质异位(FGMH )的产前超声图像特征并评价其最佳产前诊断方法。