机械原理 瞬心法求速度共18页文档

机械原理速度瞬心法的应用引言在机械原理中，速度瞬心法是一种重要的分析工具。

它可以帮助工程师和设计师理解和预测机械系统中的速度分布和运动性能。

本文将探讨速度瞬心法的基本原理，并介绍其在工程实践中的应用。

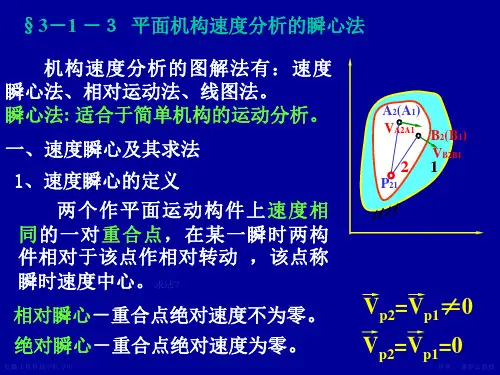
速度瞬心法的基本原理速度瞬心法是基于速度分析的一种方法。

它通过计算物体在不同位置上的速度矢量，找到所有速度矢量交点的位置，即为速度瞬心。

速度瞬心表示系统在某一时刻的整体速度特性。

使用速度瞬心法需要以下步骤： 1. 给定物体的速度矢量分布。

2. 绘制速度矢量的平行线。

3. 找到速度矢量平行线的交点，即速度瞬心。

速度瞬心法的应用领域速度瞬心法在许多领域中得到了广泛的应用，下面将介绍一些常见的应用。

1. 机械设计在机械设计中，速度瞬心法可以用来预测机械系统的运动性能。

通过计算机辅助设计软件，工程师可以根据速度瞬心的分布来优化机械系统的设计。

2. 汽车工程在汽车工程中，速度瞬心法可以用于分析汽车的悬挂系统和转向系统。

通过计算速度瞬心，工程师可以优化汽车的悬挂系统，提高行车稳定性和驾驶体验。

3. 机器人工程在机器人工程中，速度瞬心法可以用于分析机器人的运动轨迹和速度分布。

通过计算速度瞬心，工程师可以优化机器人的运动性能，提高机器人的操作精度和效率。

4. 航空航天工程在航空航天工程中，速度瞬心法可以用于分析飞机的空气动力学特性和飞行性能。

通过计算速度瞬心，工程师可以优化飞机的设计，改善飞机的飞行性能。

5. 能源工程在能源工程中，速度瞬心法可以用于分析风力发电机组的运动特性和效率。

通过计算速度瞬心，工程师可以优化风力发电机组的设计，提高能量转换效率。

结论速度瞬心法是一种重要的机械原理分析工具，可以帮助工程师和设计师理解和预测机械系统的运动性能。

它在机械设计、汽车工程、机器人工程、航空航天工程和能源工程等领域都有广泛的应用。

通过应用速度瞬心法，工程师可以优化设计，提高机械系统的性能和效率。

机械原理速度瞬心机械原理中的速度瞬心是一个非常重要的概念，它对于理解和分析机械系统的运动特性具有重要的意义。

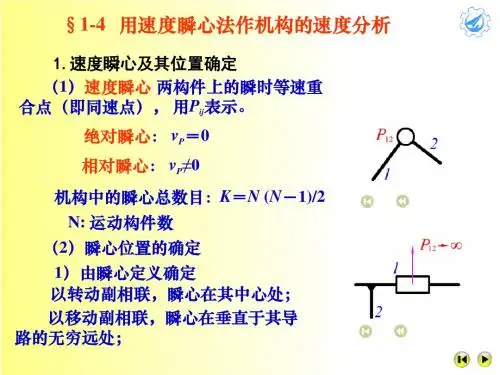
速度瞬心是指在一个给定的瞬时，系统中某一点的速度矢量的瞬时瞬心。

在实际的机械系统中，速度瞬心可以帮助我们分析系统的运动规律，设计机械结构，优化机械性能等方面起到至关重要的作用。

首先，我们来看一下速度瞬心的定义。

在机械系统中，每个点都有一个与之相关的速度矢量，该速度矢量描述了该点在某一时刻的瞬时速度。

而速度瞬心则是描述了在某一时刻，系统中某一点的速度矢量的瞬时瞬心。

换句话说，速度瞬心可以理解为系统中某一点的瞬时转动中心，该点在这一瞬时的运动状态可以用一个瞬时瞬心来描述。

其次，我们来看一下速度瞬心的应用。

在机械系统的设计和分析中，速度瞬心可以帮助我们更好地理解系统的运动规律。

通过对速度瞬心的分析，我们可以确定系统中各个点的运动状态，找出系统中可能存在的问题，进而优化系统的结构和性能。

此外，速度瞬心还可以帮助我们设计新的机械系统，提高系统的效率和稳定性。

再者，我们来看一下速度瞬心的计算方法。

在实际的工程应用中，计算速度瞬心是非常重要的。

一般来说，我们可以利用刚体运动学的知识，通过对系统中各个点的速度矢量进行分析，来确定速度瞬心的位置和性质。

在实际的计算过程中，我们可以借助计算机辅助设计软件，通过数值模拟的方法来计算速度瞬心，进而得到系统的运动规律和性能参数。

最后，我们来看一下速度瞬心的意义。

速度瞬心作为机械原理中的重要概念，对于理解和分析机械系统的运动特性具有重要的意义。

通过对速度瞬心的研究和应用，我们可以更好地理解机械系统的运动规律，设计新的机械结构，优化机械性能，提高系统的效率和稳定性，从而推动机械工程领域的发展。

综上所述，速度瞬心是机械原理中的重要概念，它对于理解和分析机械系统的运动特性具有重要的意义。

通过对速度瞬心的研究和应用，我们可以更好地理解系统的运动规律，设计新的机械结构，优化机械性能，推动机械工程领域的发展。

机械原理速度瞬心法机械原理速度瞬心法，是求解刚体运动的一种常用方法。

瞬心法简单来说就是找到相对速度为零的瞬间，然后在该瞬间分析物体的运动状态。

瞬心法主要应用于刚体在平面内的转动运动，下面我将就此展开讲解。

一、瞬心法的基本思想在瞬心法中，我们首先需要找到物体运动的瞬间中心，即瞬心。

瞬心是指在某一瞬间，物体上的任何一点到瞬心的相对速度为零。

在这种情况下，物体的运动可以看成是由两个简单的运动组合而成，一个是绕着瞬心旋转的纯转动运动，另一个是沿瞬心到该点的径线做直线运动。

二、求解瞬心的方法求解瞬心的方法主要有以下两种：1.利用速度的符号来判断瞬心位置由于瞬心是物体上任何一点的相对速度为零，因此可以通过不同点的速度符号来定位瞬心位置。

具体步骤如下：（1）选择两个质点，在剩下的质点当中任选取一个质点作为待求点。

（2）计算出上述两个质点相对于待求点在瞬间的速度矢量。

（3）根据速度矢量的相对位置确定瞬心在待求点的哪侧，方向沿待求点到相对位置两点组成的连线（即连线的延长线）。

2.利用矢量叉积法求解瞬心还有一种简单易行的方法是利用叉积求解瞬心，具体如下：（1）选取一个在物体运动方向上的固定的点O。

（2）以该点为起点，分别作向各个质点的速度矢量为方向，长度与速度的大小成比例的线段。

（3）将各个线段所在直线与以O点为起点垂直于物体运动方向为方向的直线交点，即为瞬心位置。

三、利用瞬心法解题步骤接下来，以平面内刚体运动转动为例，介绍瞬心法的解题步骤：1.标出物体上各质点的速度向量和角速度ω。

2.求出瞬心位置和速度大小。

3.利用瞬心和对应质点之间的距离求解线速度和角速度。

4.根据物理原理，利用转动定律和牛顿第二定律求解物体的运动状态。

四、注意事项在应用瞬心法时，也需要注意一些细节问题：1.瞬心法只适用于刚体的平面内转动运动，不能应用于非平面情况。

2.在用速度符号求解瞬心时，应注意速度符号判断的正确性，不要因判定瞬心位置错误而导致解题出错。

机械原理瞬心法求速度机械原理中有一种求速度的方法称为瞬心法。

这种方法基于物体绕固定轴旋转时的动力学原理，极大地简化了求解速度的过程。

本文将介绍一下瞬心法的基本原理以及如何应用瞬心法来求解物体的速度。

瞬心法基本原理瞬心法的基本原理是基于旋转运动的动力学原理。

当物体沿固定轴旋转时，我们可以将其视为一系列平行于固定轴的旋转运动的叠加。

这种旋转运动的叠加使得物体上的每一个点都会沿着一条圆弧轨迹运动，这个圆弧的圆心称为瞬心。

瞬心的位置可以用以下公式计算得出：v = v0 + a*tx = x0 + v0*t + 0.5*a*t^2其中，v 表示物体在某一时刻的速度，v0 表示物体在初始时刻的速度，a 表示物体在沿着圆弧轨迹运动时的加速度，t 表示经过的时间，x 表示物体在某一时刻的位置，x0 表示物体在初始时刻的位置。

在瞬心法中，这个公式被用来计算物体在旋转过程中的速度。

如何使用瞬心法求速度使用瞬心法求速度需要以下几个步骤：1.找到旋转轴首先需要确定旋转轴的位置。

旋转轴可以是任何固定的轴，例如绕杆旋转、绕轮旋转等。

2.确定瞬心位置瞬心是旋转轴上的一个点，它是物体上所有点沿圆弧轨迹运动叠加后的圆心。

瞬心的位置可以通过计算得出。

3.计算速度计算物体上某一点在某一时刻的速度需要使用瞬心法中的公式。

具体来说，可以通过以下步骤计算速度：•确定物体上某一点的位置和速度向量•确认该点相对于瞬心的位置，并将该位置和速度向量分解为平行于和垂直于旋转轴的两个矢量•计算沿着圆弧轨迹运动的加速度 a，一般情况下使用牛顿第二定律进行计算•使用瞬心法中的公式计算速度，并得出物体上该点在该时刻的速度瞬心法的应用瞬心法广泛应用于机械工程中，特别是在设计和分析各种旋转机械时。

下面我们以一个例子来说明如何使用瞬心法进行计算。

假设我们有一个半径为 R 的小球在平面上沿着圆周轨迹绕着一根竖直轴旋转。

现在我们想要知道小球在顶部（即与地面平行的位置）绕轴旋转的速度。

《机械原理》第三章平面机构运动分析——利用瞬心法进行机构速度分析12345P 23P 12P 15P 45P 34P 15P 12P 23P 34P 45例1：图示五杆机构，标出全部瞬心。

(1)2n n N -=1、瞬心数目：5(51)2⨯-=10=2、瞬心位置：运动副联接：非运动副联接：1223344515P P P P P 、、、、1314242535P P P P P 、、、、P 13P 35P 1412345P 23P 12P 15P 45P 34P 15P 12P 23P 34P 45例1：图示五杆机构，标出全部瞬心。

（已知P 14在AE 线上）P 14P 13P 35P 13P 35P 141342P 34P 14P 23P 12P 24例2：设已知机构各构件尺寸，原动件2的角速度为ω2，求在图示位置时从动件4的角速度ω4。

分析:已知ω2，则构件2上各点运动已知，4构件为转动构件，如果知道构件上某点的速度大小，可求出其角速度ω4。

而P 24为2、4构件的等速重合点。

解：确定机构瞬心如图所示2142441224P P P P ωω=41424lP P ωμ=2421224P l v P P ωμ=机构的传动比机构的传动比等于该两构件的绝对瞬心至相对瞬心距离的反比。

为尺寸比例尺l μω4ω224P v 请问在此位置3构件的转动中心在哪儿？P 13分析:已知ω2，则构件2上各点运动已知，4构件为平动构件，构件上某点的运动可代替该构件的运动，P 24为2、4构件的等速重合点。

P 23P 24P 12234ω2v 4P 14→∞P 34例3：如图所示的带有一移动副的平面四杆机构中, 已知原动件2以角速度ω2等速度转动, 现需用瞬心法确定机构在图示位置时从动件4的速度v 4。

2421224P lv v P P ωμ==解：确定机构瞬心如图所示式中为尺寸比例尺l μv P 24例4：如图所示凸轮机构，设已知各构件尺寸和凸轮的角速度w 2，求从动件3的速度v 3。