任务2六棱柱三视图的绘制-习题答案.

讲授
板书倾听2Fra bibliotek钟作业
习题集P26
1分钟
后记
1、让学生绘制棱柱的三视图。
2、让学生绘制棱锥及棱台的三视图。
3、体表面求点。
参考资料
1、王枕霞主编工程制图中国电力出版社
2、王枕霞主编工程制图习题集中国电力出版社
教学设计
步骤
教学内容
教学方法
教学手段
学生活动
时间分配
告知（教学
内容、目的）
1、本课任务就是绘制平面立体三视图及表面求点
讲授
板书
倾听
2分钟
引入（任务
项目）
任务1： 绘制棱柱三视图
任务2：绘制棱锥三视图
展示
启发
操作
多媒体
讨论
回答
10分钟
归纳（知识
和能力）
1、基本体的分类。
2、平面立体三视图画法。
3、体表面求点的方法
先由学生总结，教师再归纳
板书
讨论
回答
5分钟
操练（掌握初步或基本能力）
1、绘制正六棱柱的三视图
2、绘制三棱锥的三视图
教师示范
重点讲解
本次课标题：绘制棱柱、棱锥及棱台的三视图
5
授课班级
上课时间
教学目标
能力（技能）目标
知识目标
1、能运用正投影法正确绘制基本体三视图
1、了解基本体的分类
2、能准确绘制基本体表面点的三面投影
2、掌握基本体三视图的绘制方法
3、掌握基本体表面点的作图方法
能力训练任务及案例
本课学习工程制图中的平面立体，了解基本体的分类、基本体三视图的绘制方法，表面点的投影规律及作图方法等知识。
板书

工程制图第三章习题答案n e w第三章基本形体——三视图的投影班级学号姓名3-1、画三棱柱的投影图。

3-2、画出六棱柱的投影图。

3-3、画出右下图的投影图。

3-4、画出半圆拱的三面投影。

收集于网络，如有侵权请联系管理员删除3-5、画出圆台的三面投影。

3-6、画半圆拱的三面投影。

44第三章基本形体——补绘基本形体的第三投影班级学号姓名3-7、补绘基本形体的第三投影（1）（2）（3）收集于网络，如有侵权请联系管理员删除45第三章基本形体——补绘基本形体的第三投影班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除46第三章平面立体表面上的点班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除47第三章平面立体表面上的点班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除48第三章平面体的截交线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除49第三章平面体的截交线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除50第三章平面体的截交线班级学号姓名收集于网络，如有侵权请联系管理员删除51第三章平面体的截交线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除第三章平面体与平面体相交班级学号姓名收集于网络，如有侵权请联系管理员删除54第三章平面体与平面体相交班级学号姓名收集于网络，如有侵权请联系管理员删除55第三章平面体与平面体相交班级学号姓名收集于网络，如有侵权请联系管理员删除56第三章曲面体上的点和直线班级学号姓名收集于网络，如有侵权请联系管理员删除57第三章曲面体上的点和直线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除58第三章曲面体截交线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除59第三章曲面体截交线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除60第三章曲面体截交线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除61第三章曲面体截交线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除62第三章曲面体与平面体、曲面体相交班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除63第三章曲面体与平面体、曲面体相交班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除64第三章曲面体与平面体、曲面体相交班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除65第三章曲面体与平面体、曲面体相交班级学号姓名收集于网络，如有侵权请联系管理员删除66第三章曲面体与平面体、曲面体相交（应分两页）班级学号姓名收集于网络，如有侵权请联系管理员删除3-75、用辅助平面法求正立面图上的相贯线。

绘制六棱柱的三视图教学目标知识目标（1）认识六棱柱，理解六棱柱三视图的投影特征。

能力目标（1）能绘制六棱柱的三视图，会标注六棱柱尺寸。

情感目标（1）通过演示法与多媒体的教学引导学生从现实的生活经历与体验出发，激发学生学习兴趣教学手段演示教学、多媒体辅助教学教学方法讲授与课堂演示、举例相结合，任务驱动、合作探究教学过程任务一：认识正六棱柱【任务要求】：认识清楚正六棱柱的面目特征定义：顶面和底面为正六边形的直棱柱，称为正六棱柱。

问题：正六棱柱有哪几个面组成？各有什么特征？顶面侧面底面特征：顶面、底面是两个全等且互相平行的正六边形。

——特征面任务二：分析正六棱柱的三视图并绘制【任务要求】：1.分析正六棱柱的八个面在三投影面体系中的位置及投影特性；2.从三视图中找出正六棱柱上八个面的投影；3.按照给定的尺寸正确地画出正六棱柱的三视图。

小组讨论：按照给定的尺寸绘制出正六棱柱的三视图绘图步骤1：图纸布局（注意：图纸布局要合理、美观）绘图步骤2：作图（注意：严格遵循绘图的“三等”关系）任务三：正六棱柱表面上点的投影【任务要求】：想象出点在空间的位置，找准点在三视图中的位置注意：给定面上点的可见性问题及其标注课堂小结一、认识正六棱柱正六棱柱中各组成表面的特征二、分析正六棱柱的三视图并绘制分析正六棱柱各组成面在三投影面体系中的位置及投影；绘制注意点：（1）图纸布局要合理；（2）一般从最反映形体特征的视图画起；（3）严格遵循作图的“三等”关系。

三、正六棱柱表面上点的投影（1）可见点；（2）不可见点。

面2389、面34910、面561112和面61127： 与正投影面 倾斜，具有 类似性性 与水平投影面 垂直 ，具有 积聚性 性 与侧投影面 倾斜 ，具有 类似性 性
项目二：绘制正六棱柱三视图
1.如果给定了看图方向，同学们能想象出三视图的投影吗？
2.同学们可以大展身手了
规范绘图步骤：
1.建立投影坐标系
基本几何体投影-
2011.5.10
新课引入：
同学们能否举出我们身边有哪些物品 是正六棱柱形状的？
同学们展示课前自制的正六棱柱模型
新课讲授：
任务一：正六棱柱分析
1.同学们根据手里的模型分析正六棱柱的组成及与各投影面关系 两个 端面 ； 六条 棱； 六个 侧面 。 2. 同学们在自己的模型上标出各个顶点，并分 析各面，各棱的与投影面关系及投影特性。
两个底面与正投影面 垂直 ，具有 积聚性 性 与水平投影面 平行 ，具有 显实性 性 与侧投影面 垂直 ，具有 积聚性 性
Hale Waihona Puke 各棱与正投影面 平行 ，具有 显实性 性 与水平投影面 垂直 ，具有 积聚性性 与侧投影面 平行 ，具有 显实性 性
各侧面与正投影面、水平投影面侧面的位置关系：
面1278和面451011： 与正投影面 平行 ，具有 显实性 性 与水平投影面 垂直 ，具有 积聚性性 与侧投影面 垂直 ，具有 积聚性 性
2.确定三视图位置 （中心轴线位置）
3.先绘制俯视图 （利用圆六等分绘制）
4.利用长对正、宽相等、 高平齐绘制主、左视图
项目三：想一想，如果要确定正六棱柱大小， 我们需要哪几个尺寸？
项目三：转一转 想一想 画一画

能力目标
会正确运用尺规等绘图工具及AutoCAD软件绘制和 识读简单几何形体的三视图、能绘制简单几何形 体的草图。
任务3 圆柱三视图的绘制和识读
任务载体
任务资讯
任务实施
巩固练习
思考练习
任务载体
六棱柱三视图的绘制和识读
任务资讯
2.3.1 圆柱的三视图 2.3.2 圆锥的三视图 2.3.3 圆球的三视图
2.3.3 圆球的三视图 一、球的形成
圆球是由一个圆母线绕其直径旋转而成的。 母线上任一点的运动轨迹为大小不等的圆
任务资讯
2.3.3 圆球的三视图 二、投影分析 将圆球放入如图所示的三投影面体
系中，由于圆球从任意方向去看投影都 是圆，因此其三面投影都是直径相同的 圆。但三个投影面上的圆是不同的转向 轮廓素线的投影。
三个视图均为圆，其直径与圆球 的直径相等。
任务资讯
2.3.3 圆球的三视图 四、三视图的作图步骤
3）检查加深图线，整理完成后
任务资讯
2.3.3 圆球的三视图 五、球面上的特点
（1）原理和方法 球面的投影没有积聚性，且球面上也不存在直
线，所以必须采用辅助圆法求作其表面上的点的投 影。
任务资讯
动画演示：辅助圆法求球面上的点
2.3.4 圆柱三面投影图的绘制 二、圆柱三视图的作图步骤
5）检查并描深图线，完成作
巩固训练
1．绘制如图所示 的圆锥体的W面的投 影图，并画出圆锥面 上的A点、B点、C点 和D点的另两面投影。
训练要求： 正确做出圆锥体 的W面的投影图及 点的三面投影图，并 判断点的可见性。
巩固训练
2．绘制如图所示的圆柱体的W面的投影图，并画出圆柱面上的A点、B 点和C点的三面投影图。

任务2 六棱柱三视图的绘制-习题
【题一】判断题：
1. 左视图反映物体的长度尺寸和左右的位置关系。

2. 根据点的投影特性，只要给出一点的任意两个投影，便可以求出其第三投影。

3.. 平行于一个投影面，但与另两个投影面都倾斜的直线称为投影面平行线。

【题二】单选题：
1. 依据平面的投影特性，说法（）是正确的。

A、平面垂直于投影面，投影是一类相似形
B、平面平行于投影面，投影反映其实形
C、平面倾斜于投影面，投影积聚成一条直线
D、以上皆是
2. 根据投影线之间的相互关系，可将投影分为（）。

A、中心投影和平行投影
B、点投影和正投影
C、正投影和斜投影
D、中心投影和正投影
3. 三面投影体系中，三个相互垂直的投影面H、V、W延伸后将空间划分为（）个分角。

A、3
B、6
C、8
D、9
【题三】名词解释：
1、棱柱
2、六棱柱三视图的特点
3、棱柱表面上点的可见性判断原则
4、棱锥形体特征。

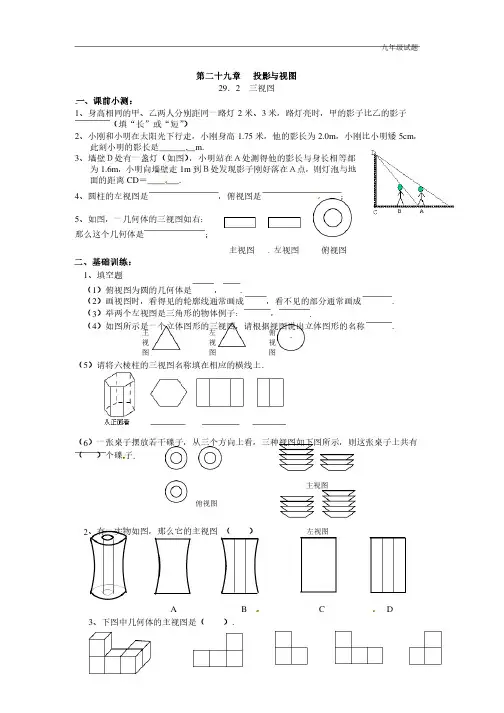
第二十九章投影与视图29．2 三视图一、课前小测：1、身高相同的甲、乙两人分别距同一路灯2米、3米，路灯亮时，甲的影子比乙的影子（填“长”或“短”）2、小刚和小明在太阳光下行走，小刚身高1.75米，他的影长为2.0m ，小刚比小明矮5cm ，此刻小明的影长是________m.3、墙壁Ｄ处有一盏灯（如图），小明站在Ａ处测得他的影长与身长相等都为1.6m ，小明向墙壁走1m 到Ｂ处发现影子刚好落在Ａ点，到Ｂ处发现影子刚好落在Ａ点，则灯泡与地则灯泡与地面的距离CD ＝_______.4、圆柱的左视图是，俯视图是；5、如图，一几何体的三视图如右：那么这个几何体是；主视图左视图俯视图二、基础训练：1、填空题（1）俯视图为圆的几何体是，.（2）画视图时，看得见的轮廓线通常画成，看不见的部分通常画成. （3）举两个左视图是三角形的物体例子：，.（4）如图所示是一个立体图形的三视图，请根据视图说出立体图形的名称.（5）请将六棱柱的三视图名称填在相应的横线上.（6）一张桌子摆放若干碟子，从三个方向上看，三种视图如下图所示，则这张桌子上共有（）个碟子.2、有一实物如图，那么它的主视图（）AB C D 3、下图中几何体的主视图是（）. 俯视图主视图左视图主视图左视图俯视图俯视图主（正）视图左视图(A) (B) (C ) (D)4、若干桶方便面摆放在桌子上，实物图片左边所给的是它的三视图，则这一堆方便面共有（有（ ） （A ）5桶 （B ） 6桶（C ）9桶 （D ）12桶5、水平放置的正方体的六面分别用“前面、后面、上面、下面、左面、右面”表示，如图是一个正方体的表面展开图，若图中“2”在正方体的前面，则这个正方体的后面是方体的前面，则这个正方体的后面是 ( ) ( )A ．OB O B．． 6C 6 C．快．快．快D D D．乐．乐．乐三、综合训练：1．小明从正面观察下图所示的两个物体，看到的是（．小明从正面观察下图所示的两个物体，看到的是（ ）2、右图是由一些完全相同的小立方块搭成的几何体的三种视图，那么搭成这个几何体所用的小立方块的个数是（的小立方块的个数是（ ）A 5个B 6个C 7个D 8个3、如果用□表示1个立方体，用表示两个立方体叠加，用■表示三个立方体叠加，那么下面右图由7个立方体叠成的几何体，从正前方观察，可画出的平面图形是 （ ）4、下面是空心圆柱在指定方向上的视图，正确的是…（、下面是空心圆柱在指定方向上的视图，正确的是…（ ）B AC D正面 A B C D (A) (B) (C) (D)5、画出下面实物的三视图：实物的三视图：第二十九章 投影与视图29．2 三视图三视图 参考答案：考答案： 课前小测：课前小测：1、短、短2、35723、15644、矩形，圆、矩形，圆5、空心圆柱、空心圆柱 二、基础训练：二、基础训练：1、(1)球，圆柱体；（2）实线，虚线；（3）圆锥，正四棱锥，倒放的正三棱柱等；（4）圆锥；（5）俯视图，正视图，左视图；（6）12.2、A ；3、C4、B5、B三、综合训练：三、综合训练：1、C2、D3、B ；4、A ；5、题图：图：主视图左视图俯视图。

Φ Φ
Φ Φ
练习3
冰淇淋
三通水管
图2
图1
如果要做一个水管的三叉接头，工人事先
看到的不是图1，而是图2，然后根据这三
个图形制造出水管接头.
练习: 根据三视图想 像物体的形状。
圆柱
圆台
手电筒 从左向右看
圆柱
正六棱柱
螺丝杆
从左向右看
圆锥
圆柱
圆台
冰淇淋 从左向右看
圆柱
四棱柱
螺丝杆
从左向右看
圆柱
镗床与铣床的区别
镗床与铣床的工作原理和性质相似。刀 具的旋 转是主 运动， 工件的 移动是 进给运 动。
镗床多用于加工较长的通孔，大直径台 阶孔， 大型箱 体零件 上不同 位置的 孔等。 由于镗 床的刀 盘和镗 杆刚性 较高， 因此加 工出的 孔的直 线度， 圆柱度 和位置 度等都 很高。
铣床也可以进行镗孔，但加工范围 较小， 精度也 较低。 铣床多 用于平 面，成 型面， 槽等加 工。
半圆球
螺丝钉
从左向右看
圆柱
圆台
圆柱
热水瓶
从上向下看
N
S
前后看 左右看
马蹄形磁铁
从上向下看
从下向上看
环的形成
本文档下载后可以修改编辑，欢迎下载收藏。
钻床和铣床的区别
钻床和铣床的区别
钻床系指主要用钻头在工件上加工孔的 机床。 通常钻 头旋转 为主运 动，钻 头轴向 移动为 进给运 动。钻 床结构 简单， 加工精 度相对 较低， 可钻通 孔、盲 孔，更 换特殊 刀具， 可扩、 锪孔， 铰孔或 进行攻 丝等加 工。铣 床是用 铣刀对 工件进 行铣削 加工的 机床。 铣床除 能铣削 平面、 沟槽、 轮齿、 螺纹和 花键轴 外，还 能加工 比较复 杂的型 面，效 率较刨 床高， 在机械 制造和 修理部 门得到 广泛应 用。

育人惠民
厚德强能
知识链接
一、基本体及其投影的概念
育人惠民
厚德强能
知识链接
二、棱柱的投影
棱线
底棱
育人惠民
由若干平面围成的立体
厚德强能
（一）棱柱的投影及其表面取点
1 ． 棱 柱 的 投 影
育人惠民
厚德强能
作图时先画反映底面实形的那个投影， 然后再画其它两面投影。
育人惠民 厚德强能
2.棱柱表面上取点
学习目标学习目标项目二简单零件图样的绘制与识读育人惠民厚德强能任务21v型铁三视图的绘制任务21v型铁三视图的绘制任务23螺栓坯三视图的绘制任务23螺栓坯三视图的绘制任务26支座三视图的绘制任务26支座三视图的绘制任务2平面体表面上点线面的识读任务2平面体表面上点线面的识读任务24顶针三视图的绘制任务24顶针三视图的绘制任务25三通三视图的绘制任务25三通三视图的绘制任务27架体三视图的识读任务27架体三视图的识读任务28轴承座轴测图的绘制任务28轴承座轴测图的绘制育人惠民厚德强能任务导入任务分析任务计划与决策任务评价知识链接任务实施育人惠民厚德强能任务引入任务引入任务23螺栓坯三视图的绘制螺栓坯是用于制作螺栓的毛坯件如有图所示
育人惠民
厚德强能
任务2.1
V型铁三视图的绘制
任务2 .2 平面体表面上点、线、面的识读
工 作 任 务
任务2.3 螺栓坯三视图的绘制 任务2.4 顶针三视图的绘制 任务2.5 三通三视图的绘制 任务2.6 支座三视图的绘制 任务2.7 架体三视图的识读 任务2.8 轴承座轴测图的绘制
育人惠民 厚德强能
1.常见平面体的尺寸标注
a)
b)
c)
d)
e)
f)

《机械制图》 第3章 基本体
资讯
3.1 基本体的投影
立体按构成不同可分为基本体和组合体。 通常将棱柱、棱锥、圆柱、圆锥、球体等简单几何体称为基本体。 按表面性质不同，又可将立体分为平面立体和曲面立体。 3.1.1 平面立体 由平面围成的立体称为平面立体，立体上相邻侧表面的交线称为 棱线。 1. 棱柱 (1) 棱柱的三视图 图3-1所示一放置在三投影面体 系中的正六棱柱。
图3-2 三棱锥的三视图
资讯
3.1.2 曲面立体 曲面立体的表面由曲面或曲面和平面组成。常见的曲面立体有圆 柱、圆锥和球体。 由于组成立体的曲面为回转面，故上述曲面立体也称为回转体。 有关回转面的几个概念如下。 回转面：一条线绕另一直线旋转所形成的运动轨迹。 回转面的轴线：不动的直线。 母线：即运动的线，回转面的母线可以是 直线也可以为任意曲线。 素线：母线位于回转面上任一位置时的线。
(a) 截切的圆锥
(b) 截切圆锥的视图
图3-17 圆锥的截交线
资讯
[例3-4] 完成被截切圆锥的视图。
(a) 求作截交线
(b) 整理图形 图3-18 圆锥的截交线
资讯
3. 球体的截交线 球体的截交线为圆，如图3-19所示。 由于截切的位置关系，球体截交线圆的投影可能为圆、直线或椭圆。 球体截交线的作图分析：当截交线的投影为圆或直线时，作图较为 简便。如是椭圆，则要利用找点的方法求得椭圆上若干点的投影后 再光滑连接各点。
资讯
若是沿圆柱轴线开一通孔，便称为圆筒。圆筒有内、外两个表面。 当截平面截切圆筒时，就会在内外表面上产生形状相同的截交线， 如图3-14所示。
(a)
(b)
图3-14 圆筒的截交线
资讯
圆筒被截切和开槽的情况如图3-15所示。

项目：绘制正六棱柱的三视图一、教学设计思路职业教育的发展方向应坚持“以就业为导向，以能力为本位”，在自主学习和“行动导向教学法”思想指导下，根据职业学校数控专业学生普遍存在理解力弱，动手能力强的生源现状，结合就业岗位对从业人员的识图能力的要求，我采用明确任务、创设情景、观察分析、兴趣激励、合作探究、实践操作、评估总结、项目拓展的教学思路，让学生“做中学，学中做”，先感性后理性，通过动脑、动手、动口，充分调动学生的学习积极性，增强学习的兴趣；通过体会成功，提高学习的乐趣，增强学习的自信心；通过对问题的探究，提高分析问题和解决问题的能力；通过生生互动、师生互动，在学习的同时，也让学生感受人与人之间和谐氛围，为今后走向社会，成为社会主义建设的优秀人才打下良好的基础。

二、教材分析机械识图是一门重要的专业技术基础课，它是研究如何运用正投影基本原理，绘制和识图机械图样的课程，它的主要任务是培养看图、绘图和空间想象能力。

本项目选自浙江省教育厅职成教教研室组编的《机械识图》项目三中的任务四。

本教材采用“项目引领，任务驱动”的方式编写，这部分内容是点、线、面等几何元素的投影特性在实际几何体中的运用，是培养学生对几何体三视图的绘制，以及尺寸的标注，为后续复杂几何体三视图的学习奠定扎实的基础。

三、教学目标根据教学大纲的要求，结合岗位的需求和学生的实际情况，制定教学目标如下：1、知识和技能目标:（1）巩固点、线、面的投影特征；（2）能绘制正六棱柱的三视图；（3）会标注正六棱柱的尺寸。

2、能力目标：（1）通过对正六棱柱的模型的制作，培养学生自主学习能力和创新设计能力，提高学生的立体感；（2）通过上课互相交流、自我评价与总结，培养学生互相协作，观察、探究、分析和解决问题、自我反思及适应社会的能力。

3、情感目标：（1）通过创设情景正六棱柱模型的制作，激发学生的好奇心、求知欲和学习的兴趣；（2）通过对正六棱柱三视图的绘制，在体验成功的过程中，增强学生学习的自信心，提高学习的乐趣；（3）通过学习，培养学生工作仔细、认真的良好工作习惯。

3-7、补绘基本形体的第三投影
（1）
（2）
班级 （3）
参考使用,交流学习 1548138554
学号
姓名
（4）
（5）
（6） 45
第三章 基本形体——补绘基本形体的第三投影 3-8、补绘基本形体的第三投影 （1）
（2）
班级
（3）
参考使用,交流学习 1548138554
学号
姓名
（4）
（5）
（6）
46
第三章 平面立体表面上的点
第三章 基本形体—— 三视图的投影 3-1、画三棱柱的投影图。
3-3、画出右下图的投影图。
3-5、画出圆台的三面投影。
班级
学号
3-2、画出六棱柱的投影图。
参考使用,交流学习 1548138554 姓名
3-4、画出半圆拱的三面投影。
3-6、画半圆拱的三面投影。
44
第三章 基本形体—— 补绘基本形体的第三投影
f'
b
ｃｄ
df
(e)
(f)
e
a
3-17、正六棱柱被正垂面 P 截断，补全截断体的 H 面投影，作出 3-18、完成平面体被平面截切后的水平投影并作出侧面投影。 截断体的 W 面投影及断面的真形。
49
第三章 平面体的截交线 3-19、补全有缺口的三棱柱的 H 面投影和 V 面投影。
班级
参考使用,交流学习 1548138554
1'
(3')
(3'')
2'
1'' 2''
3
1' 2
3-14、画出三棱柱的 V 面投影，并补全三棱柱表面上的折线 FACEDBF 的 H 面投 影及 V 面投影。

在工程设计和制造领域，三视图是表达物体形状的重要手段，正六棱柱三视图也不例外，对于理解和制作相关结构和产品具有重要意义。
正六棱柱三视图的重要性
正六棱柱三视图的绘制方法
02
根据正六棱柱的摆放位置，确定其正面方向。
确定正六棱柱的正面方向
在主视图中，绘制一个正六边形，表示正六棱柱的顶面。
绘制正六边形的轮廓
制图-正六棱柱三视图
正六棱柱三视图的基本概念 正六棱柱三视图的绘制方法 正六棱柱三视图的绘制实例 正六棱柱三视图的应用 总结与展望
正六棱柱三视图的基本概念
01
01
02
正六棱柱的定义
底面通常是一个正六边形，侧面是六个矩形。
正六棱柱是一种具有六个等边等长的侧棱和底面的几何体。
从正面观察物体得到的视图。
在室内设计中，正六棱柱三视图用于表示家具、隔断等物体的位置和尺寸，以便实现室内空间的合理布局和利用。
在建筑设计中的应用
室内设计
建筑模型
零件图
在机械制造中，正六棱柱三视图用于表示机械零件的形状、尺寸和加工要求，以确保零件的准确性和互换性。
装配图
正六棱柱三视图用于表示机械设备的装配关系，包括各个零件的位置、连接方式和配合要求，以确保设备的正常运行和维护。
实例一：简单正六棱柱的三视图
总结词：细节丰富
详细描述：这个实例展示了一个复杂的正六棱柱，其三视图在绘制时加入了更多的细节。例如，在主视图中，可以看到正六棱柱的顶面和底面；在左视图中，可以看到正六棱柱的侧面；在俯视图中，可以看到正六棱柱的顶面和底面的中心线。这些细节使得三视图更加真实地反映了正六棱柱的结构。
正六棱柱三视图的重要性和应用前景
未来发展的方向和趋势
标准化和规范化：随着工程制图技术的发展，正六棱柱三视图的标准化和规范化越来越受到重视。未来，将进一步完善正六棱柱三视图的制图标准和规范，提高制图的质量和效率。

任务2 六棱柱三视图的绘制-习题答案
【题一】判断题：
1 左视图反映物体的长度尺寸和左右的位置关系。

×
2 根据点的投影特性，只要给出一点的任意两个投影，便可以求出其第三投影。

√
3 平行于一个投影面，但与另两个投影面都倾斜的直线称为投影面平行线。

√
【题二】单项选择题：
1 依据平面的投影特性，说法〔 B 〕是正确的。

A、平面垂直于投影面，投影是一类相似形
B、平面平行于投影面，投影反映其实形
C、平面倾斜于投影面，投影积聚成一条直线
D、以上皆是
2 根据投影线之间的相互关系，可将投影分为〔 A 〕。

A、中心投影和平行投影
B、点投影和正投影
C、正投影和斜投影
D、中心投影和正投影
3 三面投影体系中，三个相互垂直的投影面H、V、W延伸后将空间划分为〔 C 〕个分角。

A、3
B、6
C、8
D、9
【题三】名词解释：
1、棱柱
棱柱是侧棱线相互平行的平面体。

当侧棱线与底面垂直时，称为直棱柱；倾斜时称为斜棱柱。

2、六棱柱三视图的特点
六棱柱的三视图中有一个视图是反映顶、底面实形的正六边形；另两个视图为相邻矩形线框。

3、棱柱外表上点的可见性判断原那么
假设点所在外表的投影可见，那么点的同面投影也可见；反之为不可见。

对不可见的点的投影，需加圆括号表示。

在平面积聚投影上的点的投影，可以不必判别其可见性。

4、棱锥形体特征
棱锥的各条侧棱线交于顶点，底面为多边形，侧面为三角形。

正棱锥的底面是正多边形，侧面为等腰三角形。

案例001与答案
案例：正三棱柱上M 点的V 面投影m ´,如图10238所示，求
该点的H 面投影m 和W
答案：
分析：从图中可知：M 点的正面投影m ´可见，因此M 点在正三棱柱的右侧面ABDE 上，为铅垂面，H 面的投影有积聚，那么M 点的H 面投影必在该侧面的积聚投影上。

作图：
〔1〕过m ´，“长对正〞向下引垂线交积聚投影ab 得m 点； 〔2〕由过m ´、m ，分别按“高平齐〞“宽相等〞作直线相交求得m 〃；
〔3〕判别可见性：由于ABDE 面的W 面投影为不可见，故m 〃也为不可见。

求作平面立体外表上MN 线段的投影，可作出平面上直线段c(f)a'〔a 〕直观图 〔b 〕投影图 图10238 三棱柱外表直线的投影
端点的各面投影，再直线连两点的同面投影点即可。

如图10244，三棱柱侧面ABED上直线MN的正面投影m´n´，该侧面ABED为铅垂面，其水平投影积聚为直线，直线MN的水平投影亦必在该积聚线上。

应用长对正可作出m、n两点投影，再由“高平齐〞“宽相等〞得m″、n″两点投影。

连接各面投影，由于ABED的侧面投影不可见，m″n″投影也不可见，用虚线连接。